环向肋增稳的薄壁圆筒结构定向拓扑优化方法

粟 华，陈伟俊，龚春林，李 鹏

(1. 西北工业大学航天学院,陕西省空天飞行器设计重点实验室，西安 710072；2. 湖北航天技术研究院总体设计所，武汉 430000；3. 西安现代控制技术研究所，西安 710065)

0 引 言

飞行器结构总体设计通常在方案设计阶段进行，该阶段设计空间大、约束少，方案需要进行多轮迭代。因此，需要详细结构模型求解缓慢的精确求解方法并不适合在该阶段使用。广泛应用于飞行器舱段的薄壁圆筒结构通常需要承受较大的轴向载荷，并且需减轻自重满足质量约束，实际应用中常采用薄壁圆筒内加筋的结构形式，以较小的附加质量使结构满足设计指标。这类结构的加筋形式将直接影响飞行器性能，因此发展一种高效快速适用于结构总体设计阶段的，兼顾结构加工性与稳定性的薄壁圆筒内加筋结构形式优化设计方法具有重要意义。

传统的薄壁圆筒加筋设计方法通常基于等效思想，通过经验公式确定均布加筋的数目与形式。Phillips等、Wodesenbet等基于结构单胞的内力分析提出了改进的等效刚度模型。王博等基于单胞结构等效刚度使用渐进均匀化方法完成了薄壁圆筒结构的快速屈曲优化。基于等效思路的设计方法能够实现结构的轻量化改进，但该类方法在设计伊始就确定了基本的加筋的布局形式，优化设计空间较小，优化能力有限。由于以最大刚度为目标的结构拓扑优化结果可以反映结构的传力路径，沿着此路径布置材料可以获得材料利用率高的轻质结构，基于拓扑优化的薄壁结构加筋形式设计方法表现出巨大的潜力。为了使拓扑优化结果具有适合薄壁结构加工的形式，Zhou等提出了一种考虑拔模约束的拓扑优化方法，可得到类拔模形式的薄壁加筋结构形式，但仅限于平面结构。张卫红等提出了一种背景网格法,可以实现任意形状的结构加筋方向拉伸约束的高质量加筋布局优化，但该方法需额外引入一套符合结构形貌的背景网格，造成前处理和求解困难。上述方法仅考虑了结构刚度最大化问题，并未考虑结构的稳定性。有研究者也在寻找兼顾薄壁结构稳定性的方法。郭中泽等、钟焕杰均将结构的屈曲系数作为附加约束引入结构拓扑优化问题，减重的同时保证了结构稳定性要求。但是这些方法都会面临较为复杂的特征值求解问题，计算耗时量较大导致其难以进行快速迭代，不适用于飞行器结构总体设计阶段的研究工作。

为了解决上述不足，让拓扑优化更加贴近工程实际，文中提出了一种高效快速且结果工艺性好，具有较好的工程应用价值的环向肋增稳的定向拓扑优化方法，如图1所示。

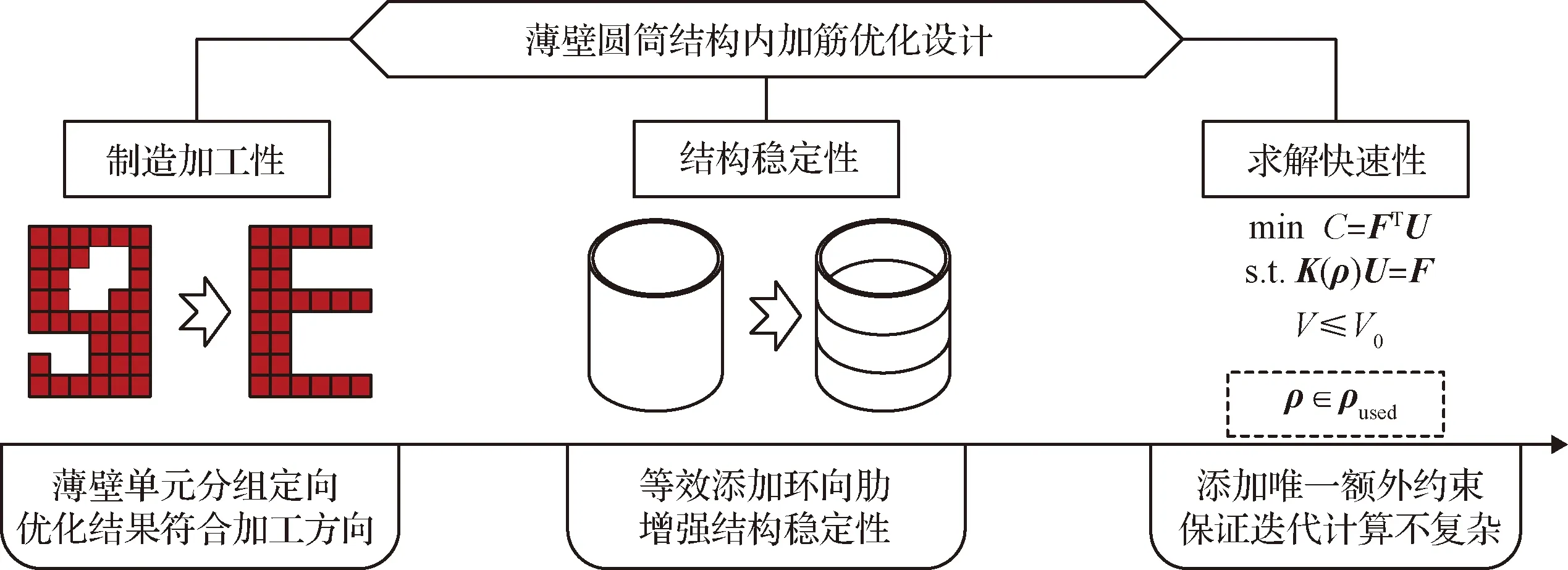
图1 环向肋增稳的定向拓扑优化方法Fig.1 The characteristics and procedure of the oriented topology optimization of thin-walled structure with circumferential rib enhancement of stability

该方法通过对表面薄壁单元的定向分组，完成设计空间的重定义，保证优化过程中壁厚方向的一致性，使结果具有较好的加工性；通过添加环向肋结构进行稳定性增强；通过重定义扑优化设计空间，仅添加唯一的单元分组约束，避免了引入额外的复杂稳定性求解过程，保证求解快速性。

首先基于有限单元定向分组方法进行设计空间重定义，提出了确定环向肋和修正设计空间的方法；然后给出了该方法基于修正设计空间的刚度最大化拓扑优化模型；最后运用该方法对运载火箭级间段结构进行优化设计，得到了具有较好实用性的优化结果并与其他优化方法进行对比分析。

1 基于经典变密度法的结构拓扑优化问题定义

变密度法参数较少，迭代稳健，构造问题模型方便，是一种广泛使用的通用拓扑优化方法，本文以该方法作为基础展开研究。

变密度法使用相对密度量描述单元存在性与材料属性之间的关系，使用相对密度概念将拓扑优化问题的设计变量从“0～1”离散型变量转变为趋向两端分布“0～1”连续变量，将不易求解的离散性问题转化为容易求解的连续性问题。综合考虑求解效率与结果准确性，选择使用各项同性材料惩罚模型(SIMP)模型：

=

(1)

式中:为相对密度下的弹性模量;为材料真实弹性模量;为有限单元相对密度;为惩罚因子，综合求解效率与结果的准确性;值取3。

对结构进行刚度最大化的拓扑优化设计，因结构的柔度与刚度为倒数关系，故该问题等效为结构柔度最小化设计问题。将柔度表示为单元密度的函数，构建体积约束下的最小柔顺度问题模型：

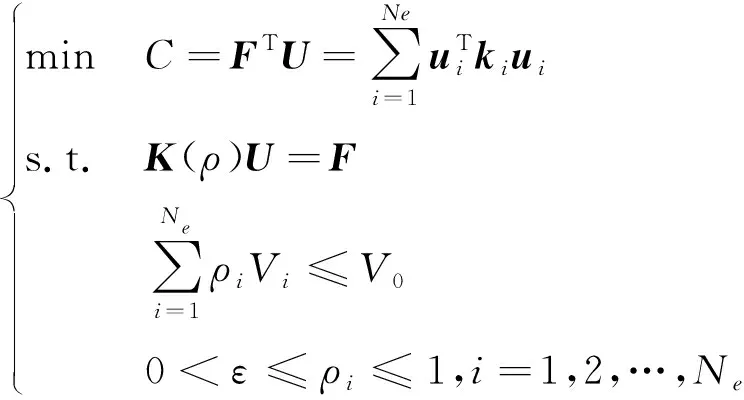
(2)

式中:为第号单元的相对密度;为避免相对密度为0造成求解困难的一小值;为设计域内单元总数;,和分别为总体刚度矩阵、位移向量和荷载向量;为第个单元的刚度矩阵，是相对密度的函数;是总体体积分数约束上限;是第个单元的体积。

目标函数对设计变量的敏感度为:

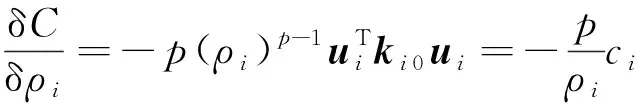
(3)

式中: 0为第个单元实际的刚度矩阵;为第个单元的应变能，负号表明向着柔度减小的方向进行。

2 依据表面单元的定向分组方法

变密度法将每个单元的相对密度作为设计变量，优化结果易存在内部空洞，所得结果虽然符合优化问题的约束，但不符合薄壁结构的实际加工特征。这里引入定向分组方法解决此问题。

飞行器舱段结构通常为薄壁蒙皮加筋形式，表面蒙皮厚度只有加筋高度的十分之一。因此常采用平面板单元模拟蒙皮区域，实体单元模拟加筋设计区域进行建模分析。由于结构的薄壁特性，实体单元可以依据外层平面单元的法向方向分成如图2所示的若干单元组。

图2 单元分组示意Fig.2 Illustration of elements group

图中最外层平面单元组成的薄壁表面为非优化区域，内部的实体单元组成内壁优化设计空间。

基于这种分组方式进行的拓扑优化过程与使用机加或化铣手段的结构制造过程在空间形式上具有一致性，易于建立有限单元间的对应关系。并且该分组过程仅在模型前处理过程中只执行一次，迭代优化过程不会引入额外约束，工作量较小，计算速度较快。因此，以单元组作为设计空间基础单位的拓扑优化方法可以在结构总体设计阶段快速得到具有较好加工性的优化结果，下面给出分组的具体方法。

记图2所示第组定向划分的实体单元组为：

={1,2,…,}

(4)

式中:为单个有限单元信息;1至为同属第分组的单元对应单元号。

记为第组单元的相对密度;为单元分组总数，同一组单元拥有相同的相对密度，即：

=1=2=…=，=1,2,…,

(5)

则有以“组密度”重定义的设计空间：

={1,2,…,}

(6)

至此，组成设计空间的基本单位从各有限单元的相对密度变为各单元组的相对密度，优化过程中将以单元组整体的有无进行迭代，保证了拓扑优化结果具有定向性。

3 引入稳定性增强的分组拓扑优化策略

由于薄壁结构容易发生屈曲失效，在考虑结构刚度的基础上还应考虑薄壁结构的稳定性。本节将给出基于欧拉稳定理论的薄壁结构环向稳定性增强策略，并将其引入连续体拓扑优化中得到增强稳定性的定向分组拓扑优化方法。

3.1 稳定性增强策略

由于刚度最大化的拓扑优化结果将保留结构传力路径上的材料，在轴向载荷作用下总会存在部分纵向分布的材料以满足结构刚度要求，而环向方向的材料是否保留没有明确的规定，因此可以通过添加环向肋的方法进行稳定性增强。

在结构总体设计阶段，通常基于无初始变形和缺陷的理想情况考虑薄壁圆筒类结构稳定性问题。大量试验结果表明，对于这种情况，基于线性欧拉屈曲理论给出的薄壁结构整体屈曲临界载荷与试验结果符合较好。因此，可采用临界应力公式快速计算薄壁结构的屈服载荷：

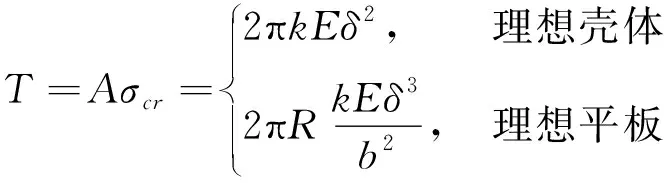
(7)

式中:为屈服载荷;为截面面积;为壳体半径;为为临界应力;为稳定系数(结构形式不同而不同);为材料弹性模量;为壳或板的厚度;为板发生屈曲方向的边长。

确定环向肋的方法如下：

(1)环向肋位置确定

在初始设计阶段首先应确保两相邻环向肋之间的壁板满足局部稳定性，如图3右上的单独环状壁板所示。图中为薄壁圆筒结构总高度，其余符号同式(7)中含义。

图3 环向肋计算中相关参数示意Fig.3 Illustration of parameters used in calculating the number of circumferental ribs

由于薄壁结构壁厚和半径相比很小，环向肋之间的局部稳定性可以近似处理为平板稳定性问题。将两环肋间的薄壁部分展开为一平面板，由试验结果统计获得，对于环向肋加强结构取0.9，则可以通过上式确定两环向加强结构的最大间距：

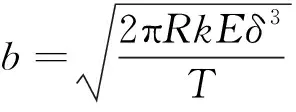
(8)

通过计算壳体总高与环向肋最大间隔的倍数，确定当前设计方案中需要引入的环向肋数目：

(9)

(10)

通过间距确定环向肋加强的位置：

=，=0,1,2,…,

(11)

(2)环向肋宽度确定

轴向载荷下环向肋加强结构的总载荷与光壳结构的总载荷计算公式：

(12)

(13)

壳的环向加劲系数为：

(14)

式中：为环向肋宽度；为两环向肋间距，对应的空间位置如图4所示。依据文献[13]中给出的实验数据点进行线性拟合可以得到用表示的，则项可表示为：

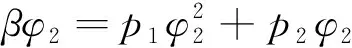
(15)

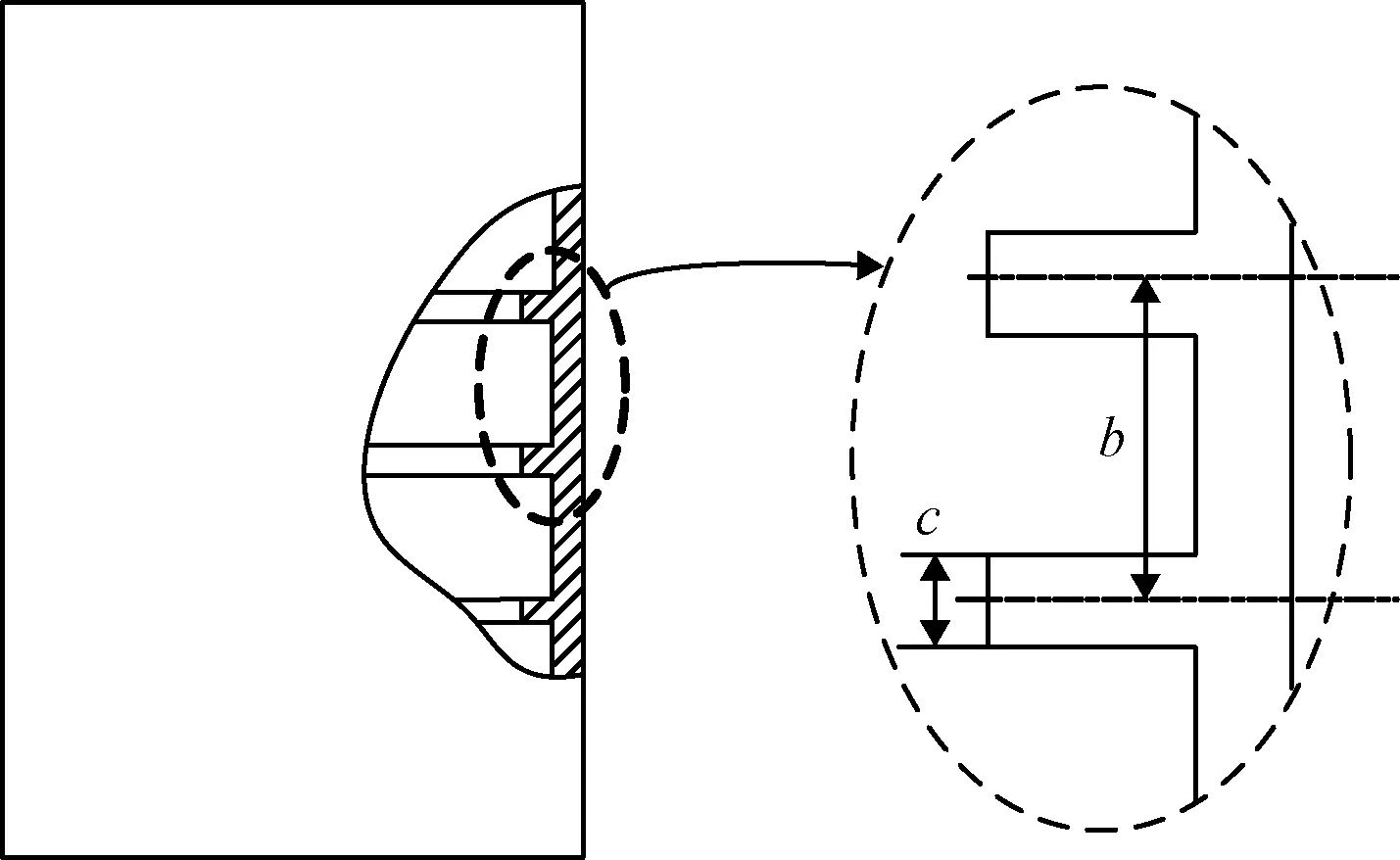
图4 环向肋间距与肋宽示意Fig.4 Illustration of spacing distance and width of circumferential rib

式中：,为线性拟合后的拟合系数，该式为二次函数，由其特性可知在可行域内必然存在唯一极值，记该值为2，将该结果代入式(14)，得到能够提供最大稳定性增强效果的环向肋宽度：

(16)

至此，需要添加的环向肋已被完全确定。这些环向结构与刚度优化后得到的纵向结构可以相互形成类似网格加强的结构，进一步提升结构的承载能力，保证该稳定性补偿策略的有效性。

3.2 修正设计变量空间

将位于环向肋体积范围内的单元剔除出优化设计空间，其单元相对密度恒为1，这样不需要其他复杂的约束条件即可保证组成环向肋的单元在优化过程中一直存在，达到在有限单元模型中等效添加环向肋的目的。本小节将给出确定组成环向肋单元的方法。

由于环向肋为定截面形式，通过指定环向肋的添加位置和纵向宽度(坐标)范围即可确定环向肋的体积范围。

1)确定环向肋基准单元的位置

由于有限单元的离散性，加肋位置与单元位置必然存在误差。本文以单层实体单元作为环向肋定位基础单元，认为当某一层单元的纵向坐标与加肋位置之间满足式(17)即可作为待定的基础单元。

|-|≤05

(17)

式中：为对应第个单元的坐标；为某一环向肋的理论位置；为单元的高度。

在添加环向肋加强的位置处，基准单元的纵向坐标存在单元中心位置距离环向肋位置小于或等于半个单元纵向高度的两种情况。

在小于半个高度的情况下，存在唯一确定的符合要求的单元纵向()坐标，即可作为第个环向肋的基准单元位置；在等于半个高度的情况下，存在两种符合要求的单元纵向坐标,，分别位于环向肋加强位置的上下对称两侧，取位于环向肋理论位置上方的作为确定环向肋位置的基本位置。

2)确定环向肋纵向宽度范围内的所有单元

环向肋的宽度应当符合最大稳定性增强的宽度。有限单元模型中对模型进了离散化处理，将对应的宽度处理为单元的层数：

(18)

式中：为对应环向肋宽度；等效为的单元层数。

基于第个环向肋的基准单元位置与所需单元层数，得到不在环向肋体积范围内的，组成实际设计空间的实体单元集合为：

={|≠(+)}

(19)

式中:=1,2,…,，=0,1,2,…,，为实际环向肋个数。基于第二节的分组定义，组成实际设计空间的单元组集合为：

={|used∈}

(20)

式中:=1,2,…,，=1,2,…,，为集合内元素总数。则在实际拓扑优化过程中使用的设计变量为各单元组的相对密度：

={|∈}=1,2,…,

(21)

式中:为实际使用的优化变量集合。至此完成对设计变量空间的修正。

3.3 建立拓扑优化流程

基于3.2小节所确定的修正后的设计空间，可以得到考虑稳定性的定向分组拓扑优化方法。该方法的数学模型为：

(22)

式中:各符号意义与式(2)、式(5)和式(21)相同，该模型已经使用分组定义并重新修正后的设计空间used，目标函数相对于设计变量的敏感度：

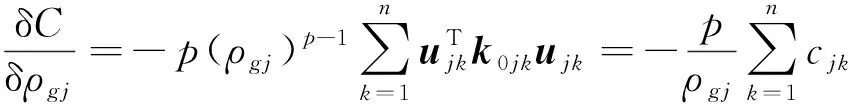
(23)

式中:,和0分别为第组中第个单元的应变能、节点位移矩阵和初始刚度矩阵，为单元组包含的单元数量，其余符号与式(21)同义。

采用最优准则法完成问题求解，环向肋增稳的定向拓扑优化方法流程如图5所示。

图5 考虑稳定性的定向分组拓扑优化方法流程Fig.5 The flow of grouping oriented topology optimization method

4 算例分析

某火箭级间段为薄壁圆柱壳体加筋结构，初始设计结果如图6所示。该级间段结构高度为720 mm，直径为2300 mm；纵向加强筋为52条；环向肋加强肋为7条。级间段的原始结构及其蒙皮厚度、横纵加强筋的高度与厚度如图6所示，蒙皮厚度1.5 mm，各加强筋的高度为30 mm，纵向加强筋厚度为15 mm，环向肋的厚度为20 mm。级间段结构的壳体与纵向、横向加强结构均使用2214牌号铝合金，材料参数依据文献[16]确定。该级间段设计承受载荷为总大小1800 kN的轴向力，该力均布在结构顶端,结构底端面固支约束。

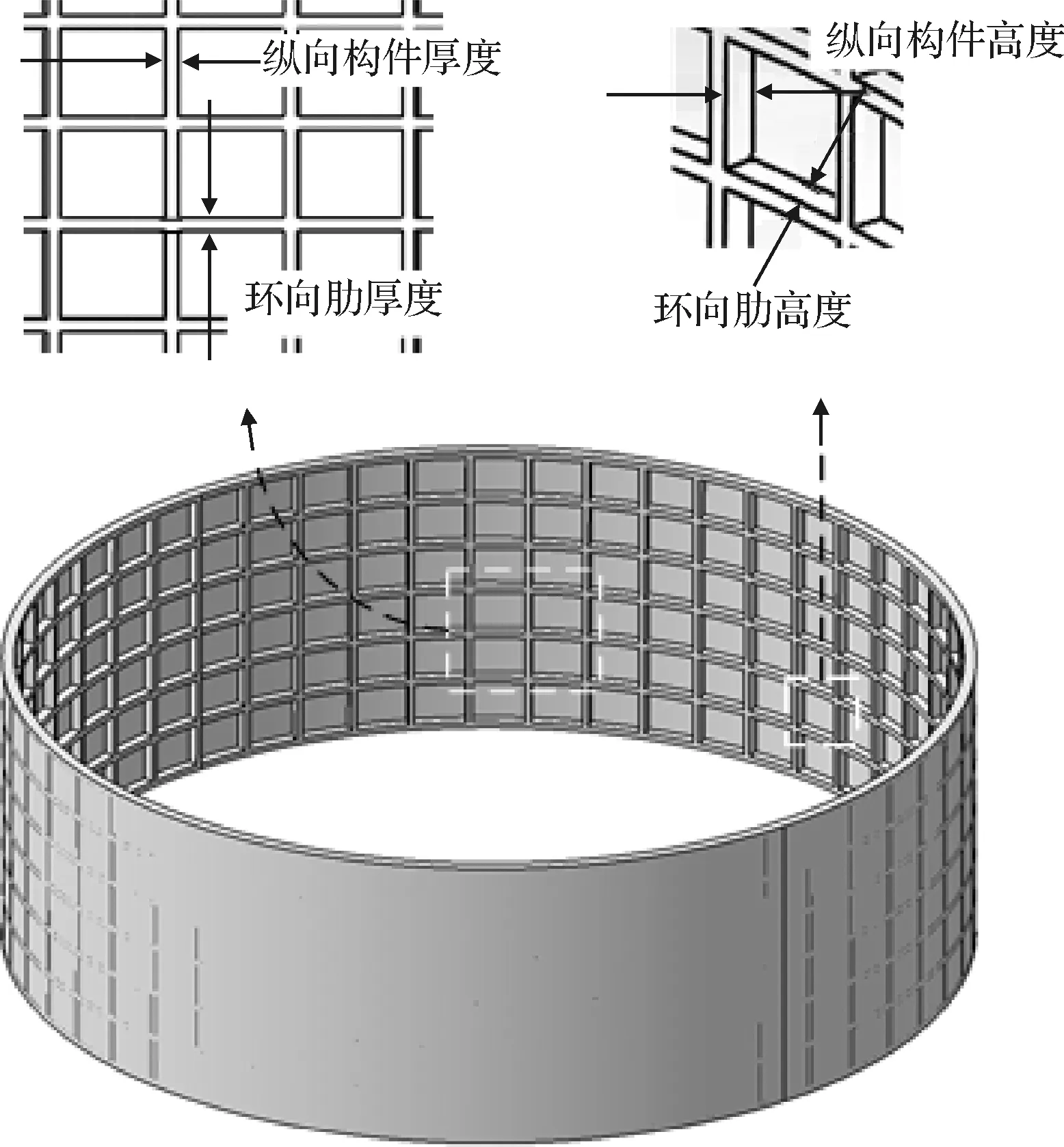
图6 火箭级间段原始结构与相关参数定义Fig.6 Original structure of rocket Interstage and definition of related parameters

采用本文提出的方法对该级间段重新进行优化设计。以连续饱满的薄壁圆筒结构为初始设计样式，建立如图7(a)所示的有限单元模型：该模型外表面为平面单元，内部为六面体实体单元，单元尺寸为10 mm，共80000个单元，81600个节点。

图7 有限单元模型与优化结果Fig.7 Finite element model and topo-optimized result

采用3.1节的稳定性增强策略，得到肋间距应小于227.1 mm，故采用5根环向加强肋，其肋宽度为28.6 mm，布置高度分别为0、180、360、540、720 mm。对设计空间进行修正，将在环向肋体积范围内的30400个单元剔除设计空间，保证环向肋结构在迭代过程中一直存在，得到实际拓扑优化设计空间，图中环状部分是不纳入拓扑优化设计空间的环向肋等效单元。

使用准则优化法对该问题进行求解，经过28次迭代得到优化结果，最终确定的拓扑形式如图7(b)所示。

由式(22)可知，该优化模型只引入了设计空间范围的额外约束，该约束只在优化空间初始化时生效一次，不涉及后续迭代，求解效率高。模拟结构外层薄蒙皮的平面单元一直存在，与加筋设计域的实体单元共节点相连，具备模拟薄壁圆筒结构外层蒙皮和内部加强构件相互作用的能力，计算结果可信。

从获得的拓扑优化结果形式上可以清晰地判断出该结构具有5个环向肋和24个纵向加强构件。这些构件由于单元定向分组的原因，内部均没有孔洞出现，边缘与外层蒙皮垂直，符合结构的薄壁特性，具有较好的加工性。

对优化结果进行稳定性分析，失稳模式如图8所示：

图8 优化方案一阶失稳形式Fig.8 First order buckling mode of optimized scheme

优化后方案的屈曲系数为10.86，说明优化后结构在设计载荷下不会发生失稳，稳定性较为充裕。

优化后的结构具有较好的加工性和稳定性，表明本文方法充分考虑了结构的薄壁特征，且该方法额外约束较少、计算效率高，是一种适合应用于飞行器结构总体设计阶段的拓扑优化方法。

5 对比与讨论

5.1 与基于经验公式设计方法的原始结构比较

对原始方案进行稳定性分析，失稳模式如图9所示。

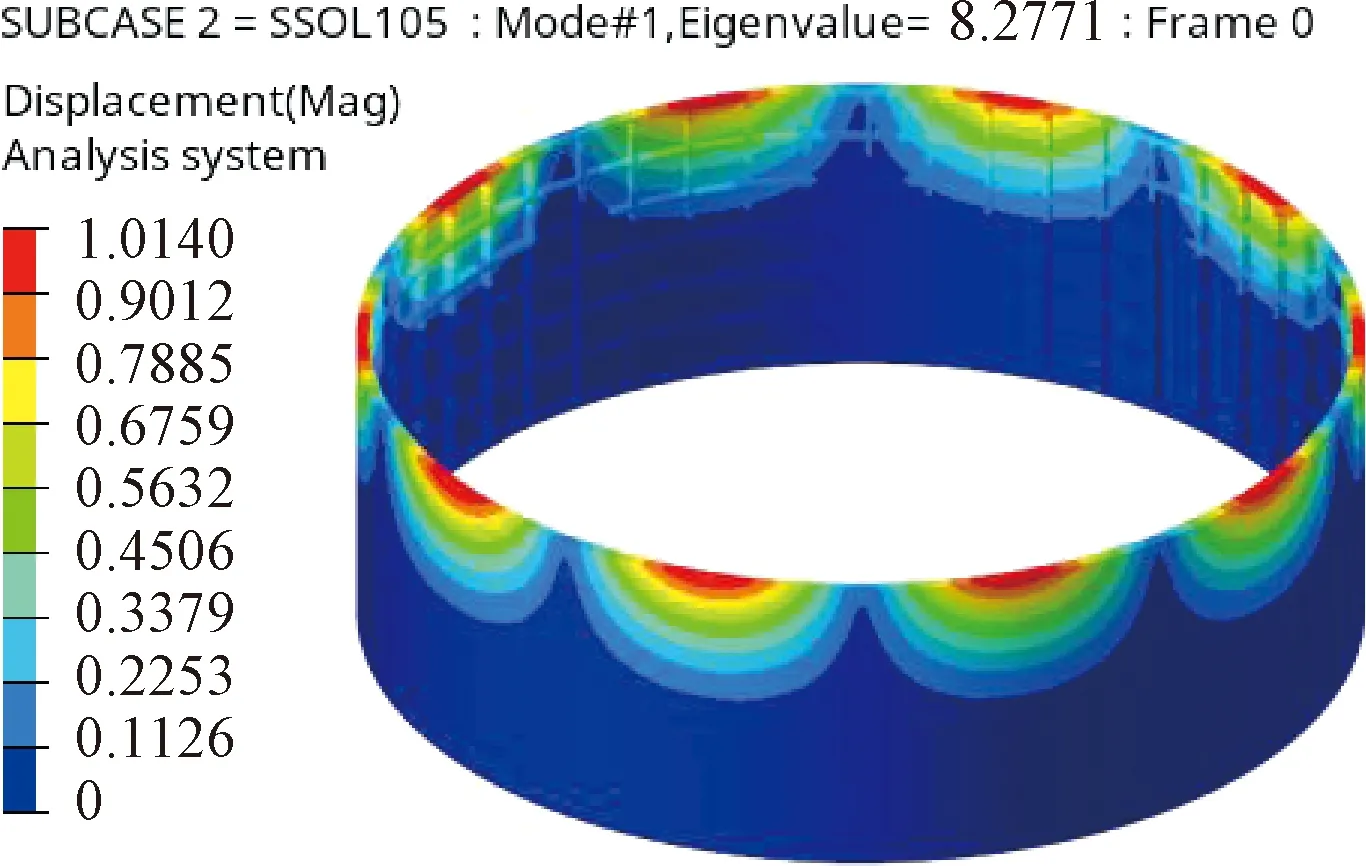
图9 原始方案一阶失稳形式Fig.9 First order buckling mode of original scheme

原始方案通过经验公式方法计算得到加筋的数目,完成了拓扑形式的定义。该方法计算快捷，组成整体结构的各构件在初始阶段就完全确定，加工性好。但是该方法的设计空间有限，不能做到沿传力路径的材料分布，材料利用率较低，结构质量大。

拓扑优化结果与结构原始方案相关参数对比如表1所示

表1方案相关参数对比Table 1 Comparison of relevant parameters

相比于原始方案，优化后的结构纵向构件与环向肋数目均显著下降，使得结构整体减重19.05%，并且能够满足设计指标，说明结构的材料利用效率得到了提升。

屈服系数上升31.21%。这是因为优化后结构的纵向材料沿着传力路径分布，分布宽度相比原始方案更大，具有更好的整体刚度，抵抗变形能力更强，使得引发结构失稳的初始形变更难产生，结构屈服系数上升。并且由于结构横纵加强构构件数目变少，形成了单胞较大的疏网格加筋形式，结构将首先发生局部屈曲。相比于原始方案首先发生整体屈曲的情况，优化后的结构更不容易发生整体塌缩，具有更高的可靠性。

5.2 与只考虑刚度最大化优化方法比较

若只考虑刚度最大化的结构拓扑优化，将得到如不含图7中环向肋的结果如图10所示。该结构具有较好的加工性，质量为109.7 kg，结构屈服系数为9.879。

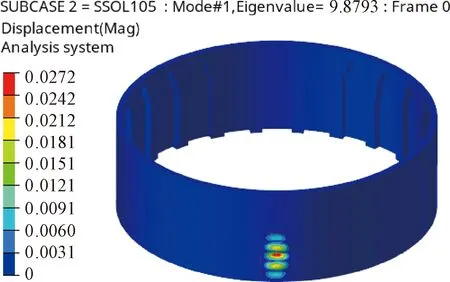
图10 优化后结构的一阶失稳模态(最大刚度方法)Fig.10 First order buckling mode of optimized scheme (max stiffness)

相比于第四节的计算结果，结构屈服系数下降9.03%，质量下降15.35%。这种变化表明：本文方法通过添加环向肋，以多付出15%的质量换取10%的稳定性补偿。虽然质量上增加了20 kg，但考虑到结构本身承受的设计载荷较大，在稳定性上的补偿最终表现为承载能力提升近180 kN，这种稳定性增加所带来整体性能提升相比于减重效果更加优越。并且由于没有添加环向肋，结构外层薄蒙皮被分为了较大纵向区域。该区域发生屈曲时虽然也是局部屈曲，但是形式相比第四节中的结果更加严重。

因此本文方法对结构性能的综合提升优于只考虑刚度最大化的优化方法。

5.3 与只考虑稳定性最大化的优化方法比较

Altair公司的optistruct结构优化求解器具有稳定可靠的求解算法，优化能力已经得到多方认可。本小节将对图7(a)所示的有限元模型使用optistruct软件进行只考虑稳定性最大化的拓扑优化。

拓扑优化后的结构形式如图11所示，可以确认大致存在5个纵向加强构件。这些构件材料分布的形式破碎，难以按照结果进行制造，可加工性很差。

图11 优化后的结构形式Fig.11 The form of optimized structure

该结构对应的一阶失稳模态如图12所示，屈服系数为6.177，相比于原始结构和本文方法分别下降了25.37%和43.12%。这是由于这种方法没有考虑结构刚度，导致材料趋向结构失稳波形的样式分布，而不沿着传力路径分布。这样得到的结构抵抗变形能力较差，载荷作用下容易发生较大扰动引发屈曲，导致稳定性系数较低。

图12 优化后结构的一阶失稳模态(最大稳定性方法)Fig.12 First order buckling mode of optimized scheme (max stability)

因此本文方法在优化后结构的加工性和稳定性方面都更具优势。

同时应注意到本文关于稳定性方面的计算采用使用于理想壳体和理想平板的经验公式(7)，直接用于加筋薄壁结构的计算会造成稳定性设计余量较大的问题。这种非稳定性最优的考虑会导致结构增重，但本文针对的是处于飞行器总体设计阶段的结构快速迭代问题，该阶段可知的载荷工况较少，设计结果会作为结构详细设计阶段的输入。相对较大的稳定性系数能够保证结构在面对一些突发干扰和初始设计阶段未曾考虑过的工况下正常工作，并且会给结构详细设计阶段提供更大的设计空间，便于进行结构精细化设计。相比于严格的稳定性系数边界约束，这种考虑稳定性的方式会带来更大的工程收益，实用性更高。

综上，相比于几种传统的设计方法，本文提出的方法能够更好地考虑薄壁结构的加工性与稳定性，得到综合性能更优的设计方案。

6 结 论

本文针对在结构总体设计阶段对飞行器舱段常用的薄壁圆筒结构进行拓扑优化时未考虑结构薄壁特性导致优化结果实用性欠佳的问题，提出了一种适用于飞行器总体设计阶段的环向肋增稳定向分组拓扑优化方法。该方法主要有两点改进：

1)通过采用定向分组的方法重新定义传统拓扑优化方法的设计变量，保证拓扑优化结果形式符合薄壁结构的加工特点。

2)引入稳定性增强策略，通过修正设计空间范围的方法等效添加环向肋，在不增加计算复杂度的基础上增强了结构的稳定性。

文中给出的仿真实例说明了该方法的有效性，后续研究中将依据优化后的加强筋壳体，进一步计算环向加强筋分布，进行参数优化，通过拓扑-参数的组合优化以获取性能更加优秀的结构，并尝试将该方法拓展至非对称性薄壁结构。