低密实度基础月壤的钻进压力建模及试验验证

周 峻，刘天喜，梁 磊，赵 阳，穆京京

(1. 哈尔滨工业大学航天工程系，哈尔滨 150001；2. 中国航天科技集团有限公司，北京 100048)

0 引 言

嫦娥五号成功带回月壤样品，为中国进一步推动载人登月及月球基地建设、火星探测等深空探测项目打下了坚实基础。针对深层月壤，嫦娥五号采用空心螺旋钻进行钻进采样，作为地外天体采样的重要方式之一，在此次及未来任务中仍面临两大难题，即如何对复杂土壤工况下钻具力载进行预测，及如何在欠数据条件下基于力载信息进行土壤性质实时反演。在实际星面采样过程中，钻采机构状态是否稳定可靠、采样策略是否需要调整、采样效率能否达到要求等问题,都需要通过力载参数尤其是钻进压力的变化进行判断，而钻进压力预测模型又是土壤性质反演的研究基础，因此，研究月壤钻进压力产生机理、建立钻进压力模型具有重要的工程意义。

目前，对钻进压力的研究仍以试验为主，但试验耗资较高，且工况覆盖度有限，因此仿真成为重要的支撑手段。在钻具-土体作用机理仿真分析方面主要分为数值和解析两种思路。在数值分析方面，部分学者采用有限元法分析月壤采样的力热问题，但由于月壤钻取过程涉及土壤颗粒的大范围交错运动，网格畸变严重，学者们因此通常将钻进问题简化为压入问题，结果与真实钻取过程偏差较大。离散元法是目前较常用的月壤钻取研究方法，将月壤离散成基于一定本构关系的大量颗粒，在三维动态仿真方面具有巨大优势。刘天喜等建立了深层月壤钻取离散元仿真模型，对采样过程中大颗粒影响、层理保持特性、钻具参数影响等进行了分析，输出了力载曲线，符合试验结果，但是由于计算量过大，只能对较短的钻进行程进行分析，无法得到完整钻进行程下的力载变化;而对于更深层月壤钻进，采用了等效方法进行仿真，但只分析了回转力矩，缺少对钻进压力的分析。陈韬等通过离散元仿真模拟了钻杆沟槽内月壤颗粒的流动和应力特性，建立了应力耦合的简化动力学模型，但没有给出钻进压力随深度变化的计算模型。因此，离散元法较适合用于复杂土壤工况下的机理或现象分析，但受限于其计算量过大的缺点，无法用于大深度钻取的力载预测。另外，因其不能进行实时仿真，无法用于后续的土壤性质反演分析。

从解析角度建立月壤钻进压力模型可解决上述难题。目前学者们普遍将钻头切削和钻杆排粉过程分开进行建模。钻头切削主要是基于被动土压力理论对切削刃作用下的土体剪切破坏过程进行建模。文献[14]还讨论了钻头处的堆积土体对钻进负载的影响，而钻杆排粉主要是基于连续介质假设对准静止态下螺纹上土体微元受力进行建模。文献[17]则将二者综合计算，给出了钻具整体的力载模型。但解析建模同样面临准确性和扩展性两大挑战。首先，以上模型均是在准静态下建立的，而实际采样过程中，钻进速度和回转速度通常无法达到准静态的等效要求，且现有模型过于关注微观作用，被动土压力理论通常应用于土木工程领域涉及大尺度宏观问题的分析中，其在切削刃受力等微观问题上的适用性还有待验证。其次，现有切削和排粉模型在分析土壤微元受力时过于理想化，只能针对细小均匀土壤进行分析，且受限于钻头构型，当面对土壤颗粒级配复杂、存在不规则石块或钻头结构复杂等情况时模型将不再适用，无法真正向工程领域扩展。此外，实践经验证明,钻进阻力主要来源于钻头，而钻杆的作用又与钻头存在复杂的耦合现象，将二者分开建模难以保证机土作用假设的合理性。因此，上述解析模型主要为月壤钻采方案初期建设提供分析思路，近年来无明显进展。

综上所述，通过离散元揭示机理、解析模型用于力载预测与反演分析是未来地外天体土壤钻采机构优化设计的可行之路，但现有解析模型在准确性与扩展性上均不成熟，因此，本文从全新视角提出一种基于宏观分析的月壤钻采解析模型，并以低密实度基础月壤进行试验验证，可有效预测钻进压力随深度的变化情况，且对于复杂工况具有良好的工程扩展性。

1 基于离散元的月壤颗粒运动分析

建立月壤钻进压力模型，首先需要了解钻采过程中钻具与月壤相互作用机理。由于地面试验过程中无法对桶内月壤进行直接观测，因此本文采用离散元仿真的方法对钻采过程进行模拟。

文献[7]中对月壤钻采过程进行了离散元仿真，给出了钻采过程中钻头附近月壤颗粒的速度场。对其分析可知，颗粒运动速度随径向距离增大而衰减；当颗粒与钻具之间达到一定距离时，颗粒运动速度几乎为零。因此，可以认为钻具只对固定范围内的月壤产生作用。

根据颗粒不同时间内的运动特点，可以将钻进过程中的月壤颗粒运动状态分为钻头入土阶段和稳定钻进阶段。首先，在钻采初期，钻头逐渐进入月壤，钻头四周的颗粒向外辐射运动，钻头四周月壤由于钻头侵入下方月壤颗粒向两侧运动而被推向上方，并且表面月壤颗粒不受约束，因此钻具周边颗粒溢出形成凸起，如图1所示。

图1 钻头入土阶段月壤颗粒运动状态Fig.1 Movement state of lunar soil particles during starting penetration

当钻头完全进入月壤后，单位时间内排开月壤颗粒的体积等于钻杆进入体积，由于钻杆粗细均匀，所以此阶段颗粒运动不受钻具几何尺寸影响，称该阶段为稳定钻进阶段，如图2所示。此阶段内，钻头附近月壤颗粒仍然呈四周扩散运动状态；而钻杆附近的颗粒由于反向螺纹的作用随钻杆回转而向上运动，最终被排出至采样处表面；月壤颗粒在上升过程中又会受到离心力、摩擦力等作用从螺纹上脱落，最终,部分颗粒在钻头与钻杆连接处附近循环运动,形成动态平衡状态；而随螺纹被带到表面的月壤也会随时间不断堆积；此外，钻头下方月壤还会有一部分进入钻具内部的取芯管中。

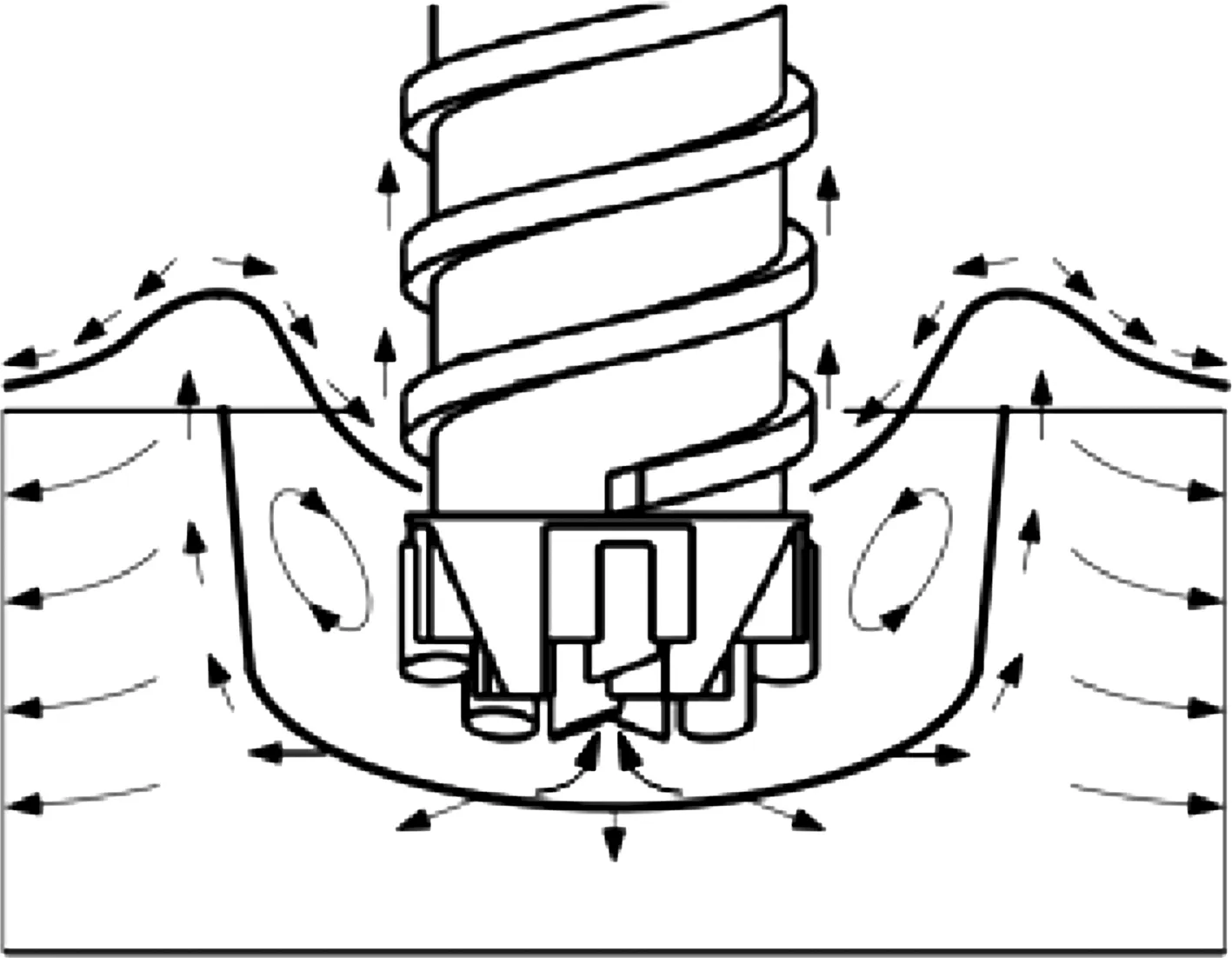
图2 稳定钻进阶段月壤颗粒运动状态Fig.2 Movement state of lunar soil particles during steady drilling

2 低密实度月壤钻进压力模型

通过离散元仿真得到月壤颗粒钻采过程中的细观变化规律，在宏观角度上建立等效的相互作用区域，结合凸形试件侵入颗粒物质所受阻力模型，提出基于稳定钻进阶段月壤颗粒密度变化的低密实度月壤钻进压力模型。

2.1 相互作用区域

根据月壤颗粒运动离散元仿真分析结果，选择钻头四周月壤为产生钻进压力的相互作用区域，并把钻头的形状简化为圆锥体，如图3所示。其中，表示相互作用区域的半径，表示相互作用区域的深度。

图3 月壤与钻具相互作用区域示意图Fig.3 Interaction zone between lunar soil and drilling tools

1)在细观角度上，钻头下方颗粒向四周扩散的状态，与月壤受压状态下的颗粒运动状态接近。因此，在宏观上认为钻进压力主要由钻头下方月壤受压产生，钻头切削和回转对钻进压力有影响，但不是主要因素。

2)在细观角度上，钻具侧方与钻具轴线的距离大于处的月壤颗粒速度几乎为零，可认为静止不动。因此，在宏观上可以将相互作用区域的侧边界等效成半径为的固定圆柱边界，并且在钻进规程不变的情况下,不随钻进深度而改变。

3)在细观角度上，钻头与钻杆交界的上方区域内颗粒循环运动，呈动态平衡。因此在宏观上为简化计算过程，使该区域内月壤密度均匀稳定，不随钻进深度发生变化。

4)在细观角度上，循环区域以上的月壤颗粒，会随钻杆回转并形成排粉，其运动不会对下方月壤运动产生影响。因此，在宏观上认为该区域与钻进压力的产生无关，可忽略。

2.2 低密实度月壤钻进压力模型

钻采过程中，钻具向下匀速直线运动且保持匀速回转，钻进压力包括钻头下方月壤承压产生的阻力。由于切削刃十分窄小，产生的切削力较小，因此其竖直分力可忽略。此外，排粉时月壤落在钻杆的螺纹上，两者之间相对位移很小，因此摩擦力也较小，可忽略不计。

通过细观颗粒运动分析，钻进压力主要由钻头下方月壤受压产生，根据文献[18]，当凸形刚体竖直压入颗粒物质且采样深度达到时，与颗粒物质相互作用的表面的受力为：

=

(1)

式中：为阻力增长梯度，该系数仅由颗粒物质的内摩擦角决定，而与侵入试件的尺寸无关；为颗粒物质的密度；为重力加速度；为刚体前驱面排开颗粒物质的体积。

在稳定钻进阶段，钻头每一时刻排开月壤的体积等于钻杆进入土体的体积，即钻头排开颗粒物质的体积不变，由式(1)可知钻进阻力与作用域内月壤密度呈正相关。此外，钻进压力还包括钻头切削力竖直分量和排粉摩擦力竖直分量，这两部分可等效为回转作用,导致相互作用区域和颗粒循环运动区域的月壤密度变化。因此，设钻进压力修正系数，得：

=·()

(2)

式中：()为采样深度达到时相互作用区域内的月壤密度。

相互作用域内各部分月壤密度的变化如图4所示，钻进距离Δ，进尺速度为，回转速度为，相互作用区域下方待采集月壤区域将有质量为的月壤颗粒进入相互作用区域中，各区域质量变化满足质量守恒定律，可得：

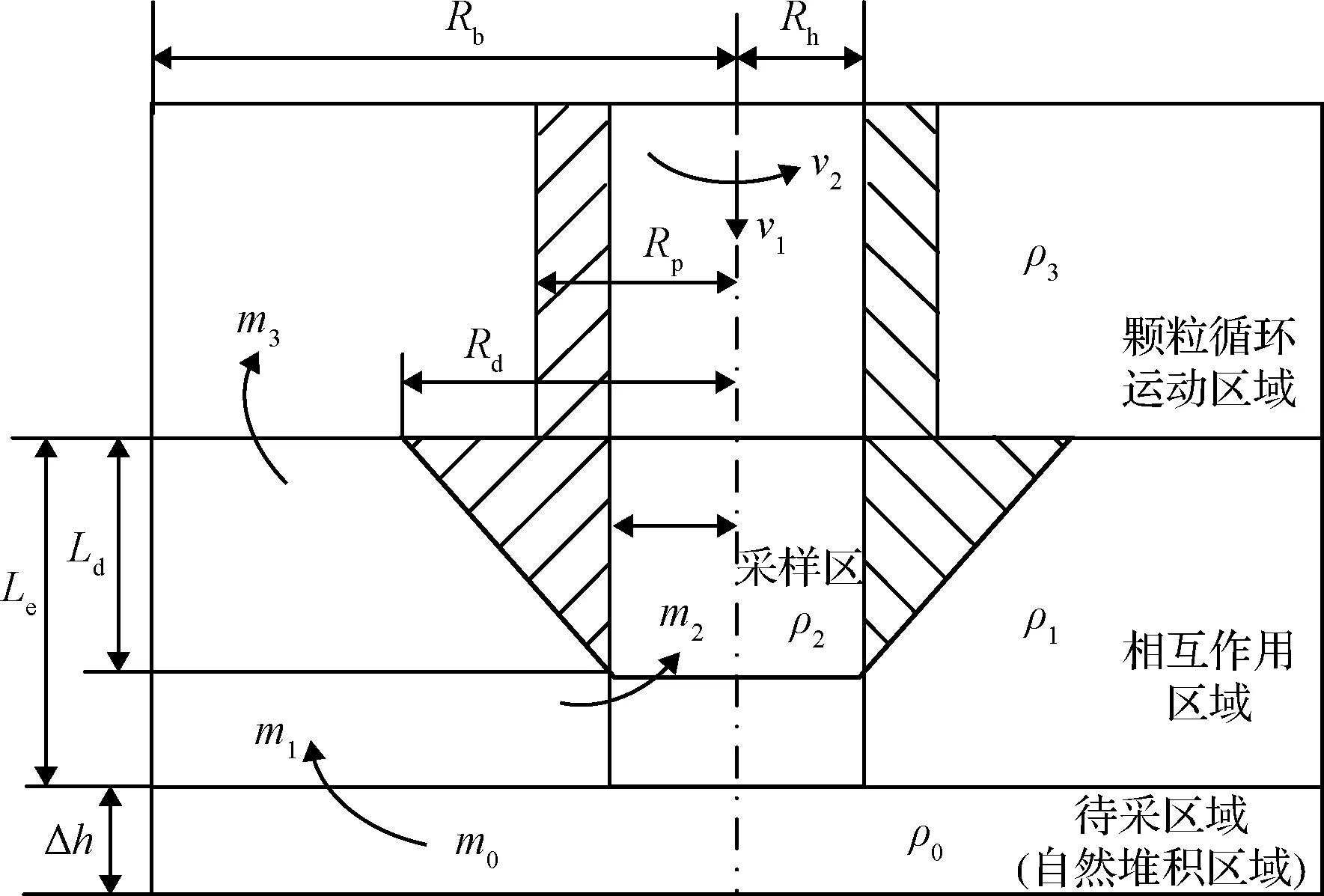
图4 钻进Δh距离后各区域的质量变化示意图Fig.4 Mass change of each zone after drilling a depth of Δhm0+m1+m2+m3=m′1+m′2+m′3

(3)

式中：为钻进Δ距离待采区内月壤质量；为当前时刻相互作用区域内月壤质量；为当前时刻采样区内月壤质量；为当前时刻颗粒循环运动区域内月壤质量；′为钻进距离后相互作用区域内月壤质量；′为钻进Δ距离后采样区内月壤质量；′为钻进Δ距离后颗粒循环运动区域内月壤质量。

式(3)可写为：

+()·+()·+=(+

Δ)·+(+Δ)·+′

(4)

式中：为钻进Δ距离待采区内月壤密度；为钻进Δ距离待采区域的月壤体积；为当前深度相互作用区域内月壤密度；为相互作用区域的体积；为当前深度采样区内月壤密度；为采样区域的体积；为当前深度颗粒循环运动区域内月壤密度；为当前时刻颗粒循环运动区域的体积；′为钻进Δ距离后颗粒循环运动区域的体积；为当前时刻的钻进深度，Δ为下一时刻钻进深度的变化量。

由几何关系可得待采区域的月壤体积为：

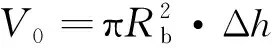
(5)

式中：为相互作用区域的半径。

相互作用区域月壤体积为：

(6)

式中：为相互作用区域的深度；为钻头的长度；为钻头的外半径；为钻孔的内半径；

钻头进样口处采样区域的体积为：

(7)

当前时刻颗粒循环区域的体积为：

=π(-)·

(8)

式中：为颗粒循环区域的深度；为钻杆的外半径。

钻进Δ距离后，颗粒循环运动区域的体积′为：

′=π(-)·(+Δ)

(9)

将式(5)至式(9)代入式(4)中可得相互作用区域内月壤密度的变化率为：

(10)

下文讨论各个区域的月壤密度变化。Mitchell等根据Apollo系列月壤样品得到月壤密度随深度变化的关系为：

=1390056

(11)

式中：为深度。

由于实际试验采用的月壤密实度与Apollo系列月壤样品存在差异，因此引入自然密度修正系数，则相互作用区域下方月壤密度为：

=·

(12)

相互作用区域中部分月壤颗粒会进入取芯管内的采样袋中，将采样袋中月壤颗粒状态简化为自然堆积状态。由于实际采样时样品不可能恰好充满采样袋，因此，设采样密度修正系数为，得到采样区月壤密度为：

=·

(13)

颗粒循环运动区域内的月壤密度均匀且不随钻进深度变化，取值等于被采样月壤的平均密度。

将式(10)、式(12)以及式(13)代入式(2)中，即可得低密实度月壤钻进压力模型，模型中的钻进压力修正系数可以通过试验得到。

3 地面钻采试验

3.1 地面设备及工况

为验证模型的准确性，采用70%密实度的基础模拟月壤进行地面钻采试验。采用钻具综合性能测试设备作为试验系统平台，该平台主要由负载施加单元和钻进驱动单元组成，如图5所示。其中，负载施加单元主要用来支撑固定钻采机构并承载模拟月壤，使钻具能在相应位置完成采样工作；钻进驱动单元又由回转驱动部件、进尺驱动部件、冲击驱动部件和提芯驱动部件组成，各部件紧密配合，完成钻具向下钻入月壤并将月壤收集至取样袋的工作。

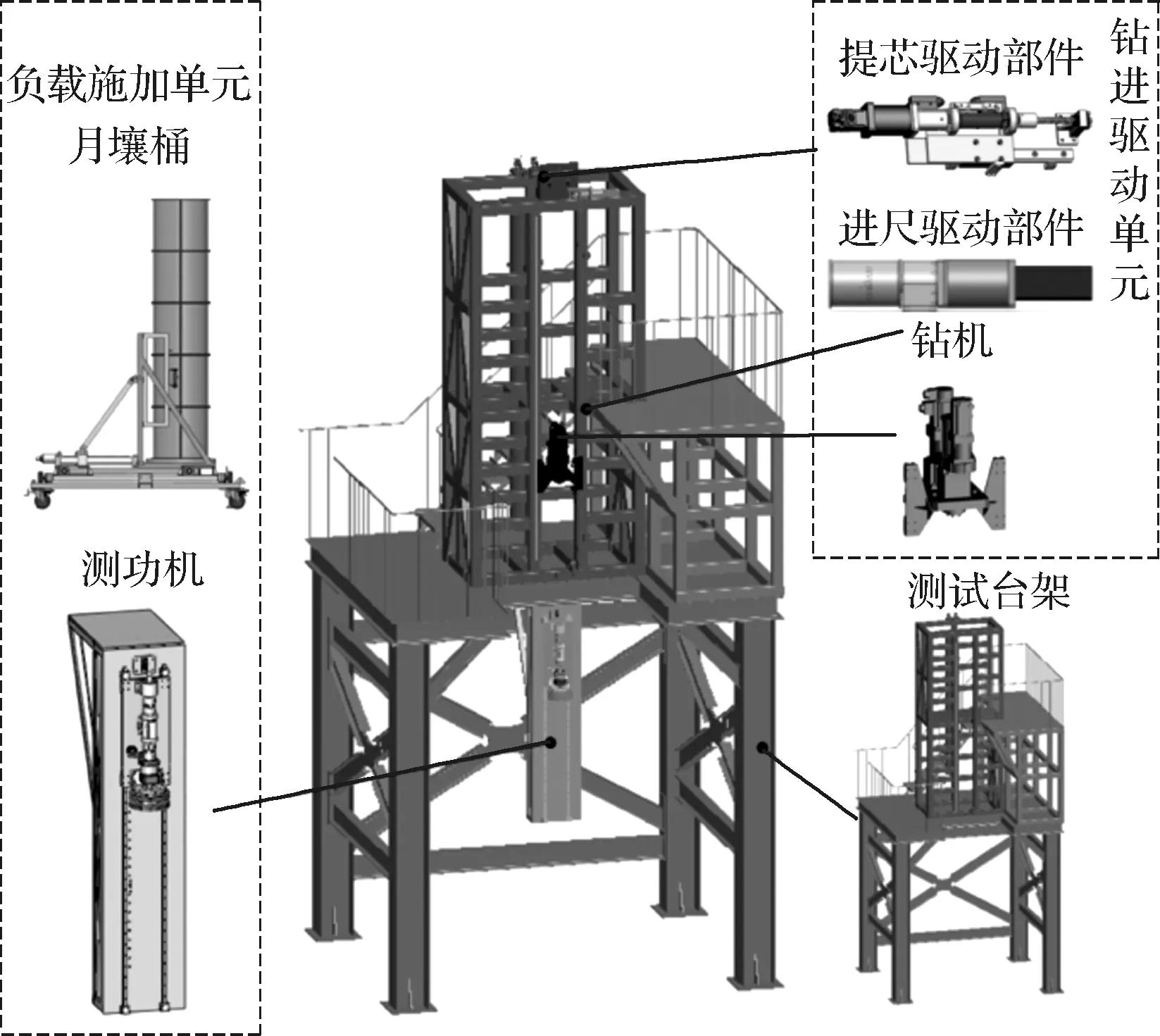
图5 钻具综合性能测试设备示意图Fig.5 Comprehensive performance testing equipment for drilling tools

基础模拟月壤的粒径分布如表1所示，试验月壤的平均密度为1.58 g/cm。由于不存在大颗粒，密度变化符合自然堆积状态，不会出现突变，因此钻进压力变化较为平稳。

表1 模拟基础月壤粒径分布Table 1 Particle size distribution of basic lunar soil simulant

采用的钻具几何尺寸如表2所示，模型计算时采用与实物相同的几何参数。

表2 钻具几何尺寸Table 2 Physical dimensions of the drilling tool

试验矩阵如表3所示，钻进比为回转速度与进尺速度之比。

表3 各试验工况的钻进规程Table 3 Drilling procedures for each test condition

3.2 试验结果

图6为钻进过程中月壤及钻杆的状态，排出的月壤会在钻孔附近堆积，与离散元仿真结果一致。图7为部分采样结果。

图6 地面钻采试验过程Fig.6 Ground drlling test

图7 试验中收集到的部分样品Fig.7 Some samples collected during the test

图8中虚线表示各个工况下滤波后的钻进压力随深度变化的曲线。由试验结果分析可知，在钻进开始阶段钻进压力增长缓慢，当达到某一时刻，钻进压力开始快速增大；钻进压力与钻进比有关，钻进比越大，相同深度处的钻进压力越小；钻进压力的增大速率同样与钻进比有关，但是钻进比越大，增大速率反而越小。

图8 模型计算结果与地面试验结果对比Fig.8 Comparison of simulation results with ground test results

受限于试验设备，采集到的钻进压力波动较大，将试验数据滤波后，经计算得到压力模型中的相互作用区域半径与钻进压力修正系数。不同工况下相互作用区域半径的值满足：

=00235301261

(14)

式中：为钻进比。由式(14)可知相互作用区域半径随钻进比增大而增大，最后趋于稳定。从细观月壤颗粒运动角度分析，钻进比越大，回转的作用越强，钻头附近颗粒的环向流动能量就越大，所带动的周边颗粒就越多，但是能量是逐渐衰减的，越向外侧，能量衰减越快，并且当到达一定范围后能量会急剧衰减，因此钻进比达到一定程度后即使再增大，作用域的边界半径也不会明显增大，最终趋于稳定。

同理，不同工况下钻进压力修正系数的值满足：

=-11791725+7415

(15)

由式(15)可知，钻进压力修正系数随钻进比的增大而减小。从细观月壤颗粒运动角度分析，回转作用越弱，相互作用区域颗粒环向流速减慢，主要向径向运动。反映到宏观上就是,相互作用区域内的月壤密实度越大，竖直方向上月壤承压变形越剧烈。

4 模型分析

4.1 模型计算结果与试验结果对比

图8中实线代表模型计算后的结果，与试验结果对比可知，模型预测的钻进压力变化趋势与试验结果基本一致，虽然无法完全模拟出实际试验时力载波动变化，但是偏差在量级范围内。此外，该模型还反映出了钻进规程(钻进比)与钻进压力之间的关系，钻进比越小，钻进压力越大且随钻深增加而增长的速度越快，符合离散元仿真得到的月壤颗粒运动细观规律和地面试验得到的宏观规律。因此，本文提出的相互作用区域等效方法可以建立钻采过程中宏观现象与细观颗粒运动之间的联系。基于此方法建立的低密实度基础月壤钻进压力模型能够对钻采过程中的钻进压力进行模拟预测。

4.2 模型可扩展性分析

本模型将钻头和钻杆视为一体，从宏观角度分析月壤颗粒的流动规律以及与钻具之间的相互作用，避免了基于微元分析的小尺度局限，无论与钻头接触的是低密度月壤、高密度月壤还是不同尺寸、不同形状的石块，无论钻头构型细节如何变化，均可转化为相互作用区域内月壤等效密度的变化，体现为相互作用区域半径、钻进压力修正系数等相关参数，可由试验测得。该模型在试验修正后可应用于其他土壤工况，相关参数也可通过土力学等理论不断细化和优化，提高仿真精度，在本模型基础上研究其逆过程，则可建立土壤性质反演模型，因此该模型具有良好的可扩展性。

5 结 论

本文通过离散元仿真明确了月壤钻采过程中土壤颗粒的运动规律，从宏观角度建立了新型月壤钻进压力解析模型，通过低密实度基础月壤钻进试验验证了模型的正确性，并得到如下结论：

1)钻采过程中钻头下方月壤颗粒运动呈现向四周扩散状态，钻具周边一定距离范围外的颗粒可近似为静止不动，基于此提出相互作用区域等效方法，该区域为半径和高度一定的圆柱区域，且半径与钻进规程相关。

2)钻进压力主要与钻头下方月壤密度有关，钻进过程中相互作用区域内各部分月壤密度相互转化，利用质量守恒定律建立月壤钻进压力模型，进行了低密实度基础月壤地面钻采试验，钻进压力仿真预测曲线与试验曲线吻合度较高。

3)相互作用区域半径和钻进压力修正系数均与钻进比有关，在70%密实度基础月壤条件下，=00235301261,=-11791725+7415，钻进比越小，钻进压力越大且随钻深增加而增长的速度越快。

4)该模型避免了微元分析的尺度局限性，可通过修正系数适应不同钻采工况，便于优化和反演建模，具有良好的可扩展性。

综上所述，本文建立的钻进压力模型能够为复杂机土作用建模提供新的角度和思路，为月球及其他天体采样技术的研究提供理论支持。