基于能量泛函变分原理的三层有砟轨道垂向振动带隙分析

冯青松，廖宝亮，郭文杰，付景文，陆建飞

(1.华东交通大学 铁路环境振动与噪声教育部工程研究中心，江西 南昌 330013；2.江苏大学 土木工程学院，江苏 镇江 212013)

我国在兴建铁路客运专线的同时，也对既有线进行了大面积的提速改造，用以缓解我国目前紧张的铁路运输状况。在经济欠发达和人口流动量有限的地区，客货混运仍然是该类地区铁路运输的主要方式。此外，列车在轨道上运行时产生的振动以及辐射的噪声会影响乘客的舒适度及沿线居民的生活品质，因而轨道结构的振动及其控制是一大热点课题。固体物理学研究表明周期结构可以产生带隙，并且处于某个带隙频段的弹性波在结构中会迅速衰减而无法传播，这是周期性结构所具有的一大重要物理特性。有砟轨道结构通常是沿铁路线路纵向周期分布的，因而可以视为一种人工周期性结构而具有带隙特性。通过对轨道结构有关参数进行优化设计，可以达到优化其带隙频率的位置与宽度的目的，提高其减振效果，从而为轨道结构减振设计提供新思路。因此，研究周期性有砟轨道结构中弹性波传播特性对于其振动与噪声控制技术的发展具有重要意义。

目前国内外已有许多学者对轨道结构中弹性波的传播特性进行了研究。Thompson等[1]率先进行了轨道结构振动特性的研究，基于行波分析法，建立了连续支撑约束的周期性结构模型，但没有用周期性结构的带隙特性来对其进行分析。Abe等[2]在Thompson研究工作的基础上，将轨道结构改为离散支撑约束，同时将轨枕视为Timoshenko梁，考虑其剪切效应，进而得到结构的振动带隙特性曲线，但并未分析其成因。

自从把带隙特性引入轨道结构的研究中，各种轨道结构带隙特性的求解方法不断涌现。Grassie等[3]把轨道结构视为一种周期梁结构，并采用广义状态矩阵法来推导其导纳函数，最后通过相关的实验进行了验证。Sheng等[4-5]提出了一种基于波数的周期支撑结构在固定和移动谐波荷载作用下结构动态响应的计算方法——2.5维有限元法，并得到了振动传播常数随频率的变化曲线。Nordborg[6]基于傅里叶变换并针对周期性轨道结构的振动响应特性进行了分析，指出在较宽且明显的衰减域内钢轨噪声辐射较小，并且“pinned-pinned”振动可以在周期性连续支撑的轨道中自由传播。易强等[7]基于Bloch定理和传递矩阵法分析了有砟轨道结构的带隙特性，并基于功率流方法分析了弯曲波能量在有砟轨道结构中的传播特性。

可见，国内外学者提出了许多方法来研究周期性轨道结构的振动特性，而这些研究基本是依赖于直接求解轨道结构的振动微分方程组，因而所建立的模型基本为单层或双层模型。结构自由度的增大会大大增加求解振动微分方程组的困难，故鲜有研究选择三层或以上的轨道结构作为研究对象。然而运用能量法求解周期性有砟轨道结构的带隙特性时可以先将振动微分方程等效为积分的弱形式，从而得到各组分能量，在得到系统总能量泛函后对未知系数求极值可转化为求解特征值问题，进而求得结构带隙特性，因而可以避免直接求解复杂的微分方程组，同时也能适用于多自由度、多维度的结构模型。因此，本文以客货混运铁路为研究对象，建立了三层周期性有砟轨道模型，并提出了一种基于能量泛函变分原理及平面波级数展开的混合方法，用以研究轨道结构中弹性波的带隙特性。

1 分析与计算方法

1.1 计算模型

传统的客货混运有砟铁路轨道结构可以简化为连续的弹性三层梁模型[8]，由于轨道结构沿纵向中心线对称，可取其一半进行分析，见图1。轨道结构主要由钢轨、扣件、轨枕、道床和路基组成，其中钢轨考虑为连续梁，扣件仅考虑其垂向刚度，轨枕等效为质量块，道床在考虑其垂向支承刚度的同时又将其等效为质量块，路基仅考虑其支撑刚度。以上所述中考虑为刚度的均可等效为线弹簧。

图1 三层有砟轨道结构简化示意

轨道结构可视为沿纵向周期分布的人工周期结构，取其中一个元胞进行分析。在元胞中建立平面直角坐标系，x为横坐标，w、z和y分别为钢轨、轨枕和道床的垂向位移；钢轨最小周期(即扣件间距)为l0，轨枕质量为mb，道床质量为ms；扣件垂向刚度为kp，道床垂向支撑刚度为kb，路基支撑刚度为ks。

1.2 理论公式

能量泛函变分原理应用的前提是得到系统的总能量泛函，而系统的总能量为应变能与外力势能之和，其中外力势能与系统的动能互为相反数。因此，为了得到系统的总能量泛函，需要先求得钢轨的势能与动能、扣件的势能、轨枕的动能、道床的势能与动能以及道床下弹性路基的势能。

1.2.1 钢轨势能与动能

已有研究表明[9]，轨道结构的“pinned-pinned”频率与扣件间距有关。由于扣件间距较小，如果将钢轨考虑为欧拉梁，所求得的“pinned-pinned”频率结果误差较大，因此本文将钢轨考虑为Timoshenko梁。

Timoshenko梁的振动微分方程为[10]

(1)

式中：w为垂向位移；θ为钢轨转角；ρr为钢轨密度；Er为钢轨的杨氏模量；Ir为截面惯性矩；kr为剪切系数；Gr为剪切模量且Gr=Er/[2(1+μ)]，μ为泊松比；Ar为截面面积；ω为结构特征频率。

根据能量泛函变分原理[11]，将梁结构振动微分方程等效为积分的弱形式，从而可以得到钢轨的应变能的积分表达式为

(2)

式中：l0为扣件间距。

根据固体力学能量变分问题解法中的Rayleigh-Ritz法[12]及平面波级数展开，同时考虑其满足Bloch周期定理，该Timoshenko梁的位移场为

(3)

式中：w(x)为垂向位移；θ(x)为钢轨转角，展开项均为(2c+1)项；j为展开项序号；k为波数；x为梁的横坐标；i为虚数单位；λ(x)为关于x的试函数行向量；Q1、Q2为未知系数列向量，其表达式为

(4)

Q1={w-c,w-c+1,…,w0,…,wc}T

(5)

Q2={θ-c,θ-c+1,…,θ0,…,θc}T

(6)

轨枕和道床的竖向位移分别为z和y，定义向量为

QH={Q1H,Q2H,z,y}

(7)

式中：QH、Q1H、Q2H分别为Q、Q1、Q2的复共轭转置向量，并且QH、Q1H、Q2H均为行向量，Q、Q1、Q2均为列向量。

将式(3)和式(7)代入式(2)可得

(8)

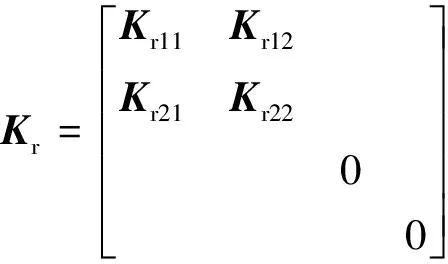
(9)

(10)

(11)

其中，Kr11、Kr12和Kr13中的第a行b列元素为

(12)

(13)

(14)

其中，a,b∈[1,2c+1]，且a,b∈N。

钢轨的动能可表示为

(15)

式中：ρr为钢轨密度；ω为结构特征频率。

将式(3)和式(7)代入式(15)可得

(16)

式中：

(17)

其中，Mr为质量矩阵，且满足

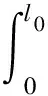
(18)

(19)

对于Mr11及Mr22中的第a行b列元素，则有

(20)

(21)

式中：a,b∈[1,2c+1]，且a,b∈N。

1.2.2 扣件弹性势能

考虑钢轨与轨枕连接处扣件的弹性势能，其表达式为

(22)

式中：kp为扣件垂向刚度。

位移差值为

w-z={λ,O3,-1,0}·Q

(23)

式中：O3为(2c+1)维元素为零的行向量。

将式(23)代入式(22)可得

(24)

式中：ζ11=kpλHλ，为(2c+1)×(2c+1)维矩阵；ζ13=-kpλH，为(2c+1)维列向量；ζ31=-kpλ，为(2c+1)维行向量；O4为(2c+1)×(2c+1)维零矩阵；O5为(2c+1)维元素为零的列向量。

ζ11中的第a1行、第b1列元素的表达式为

ζ11(a1,b1)=kpexp[i(b1-a1)π]

(25)

ζ13为列向量，则其中的第a2行元素的表达式为

ζ13(a2,1)=-kpexp[-i(a2π+kl0/2)]

(26)

ζ31为行向量，则其中的第b3行元素的表达式为

ζ31(1,b3)=-kpexp[i(b3π+kl0/2)]

(27)

式中：a1,b1,a2,b3∈[1,2c+1]，a1,b1,a2,b3∈N。

1.2.3 轨枕的动能

由于轨枕被视为集中质量，因此不考虑其应变能，而只考虑其动能，并且可由下式计算得到

(28)

式中：mt为轨枕质量；O1为(4c+2)×(4c+2)维零矩阵。

1.2.4 道床势能与动能

道床具有竖向刚度，考虑其位移势能为

(29)

式中：kb为道床刚度；z为轨枕竖向位移；y为道床竖向位移。

将道床质量考虑为集中质量，其动能表达式为

(30)

式中：mb为道床等效质量；ρb为道床沿线路中轴线考虑为一半后的线密度，且满足mb=ρbl0；O2为(4c+3)×(4c+3)维零矩阵。

1.2.5 道床下弹性路基势能

道床下路基作为弹性体，需考虑其弹性势能，其表达式为

(31)

式中：ks为路基垂向刚度。

1.2.6 总能量泛函

轨道结构系统的总能量泛函可表示为

Π=Ur+Us+Ub+Up-Tr-Tt-Tb

(32)

对未知系数求极值，即

(33)

于是将系统的振动问题转化为求解特征值的问题，可表示为

(K-ω2M)Q=O6

(34)

式中：K为系统总刚度矩阵；M为系统总质量矩阵；O6为(4c+4)维元素为零的列向量；ω为特征频率。

图1所示有砟轨道结构可视为沿轨道纵向分布的人工周期结构，其简约Brillouin区范围为[-π/l0，π/l0]，则沿该范围对式(34)进行求解，可以得到三层有砟轨道结构的频散曲线图(带隙图)，从而得到其带隙特性。

2 垂向振动带隙特性分析

垂向振动、纵向振动以及扭转振动是轨道结构振动的主要形式，本文选择轨道结构的垂向振动作为研究对象，分析其带隙特性。为此，本文分别通过能量-平面波级数混合法与有限元法计算与绘制图1所示三层周期性有砟轨道结构的垂向振动带隙图，其中所采用的轨道结构参数见表1[8](表1中所示参数均是考虑轨道结构一半之后所取的计算参数)。随后将所得结果进行对比，验证能量-平面波级数混合法计算周期性轨道带隙的准确性。

表1 有砟轨道结构计算参数

值得一提的是，本方法中将钢轨的位移场展开后，其还涉及截断项个数的取值，而由于本方法的收敛性较高，与截断项个数有关的参数c的取值为3时便明显收敛，因此将该值设定为之后的计算分析中c的取值。

轨道结构带隙中1 500 Hz以上频率带隙均为“pinned-pinned”频率，因此为简化分析与研究过程，仅研究0～1 500 Hz范围内的带隙频率。基于能量-平面波级数混合法并运用MATLAB软件编程计算，绘制得到的0～1 500 Hz范围内三层有砟轨道结构带隙见图2(a)，用时5.2 s。

为了分析与研究的方便，引入无量纲参数m，用以代替波数k，且满足关系式：m=kl0/π。由1.2.6节知波数k的取值范围为[-π/l0, π/l0]，因此参数m的取值范围为[-1,1]。

为方便分析低频频段带隙，将图2(a)局部放大后见图2(b)。显然，三层周期性有砟轨道结构在0～1 500 Hz范围内形成了四阶带隙，它们的范围分别为0～54.74 Hz、69.93～135.2 Hz、177.5～265.6 Hz、1 082～1 130 Hz。

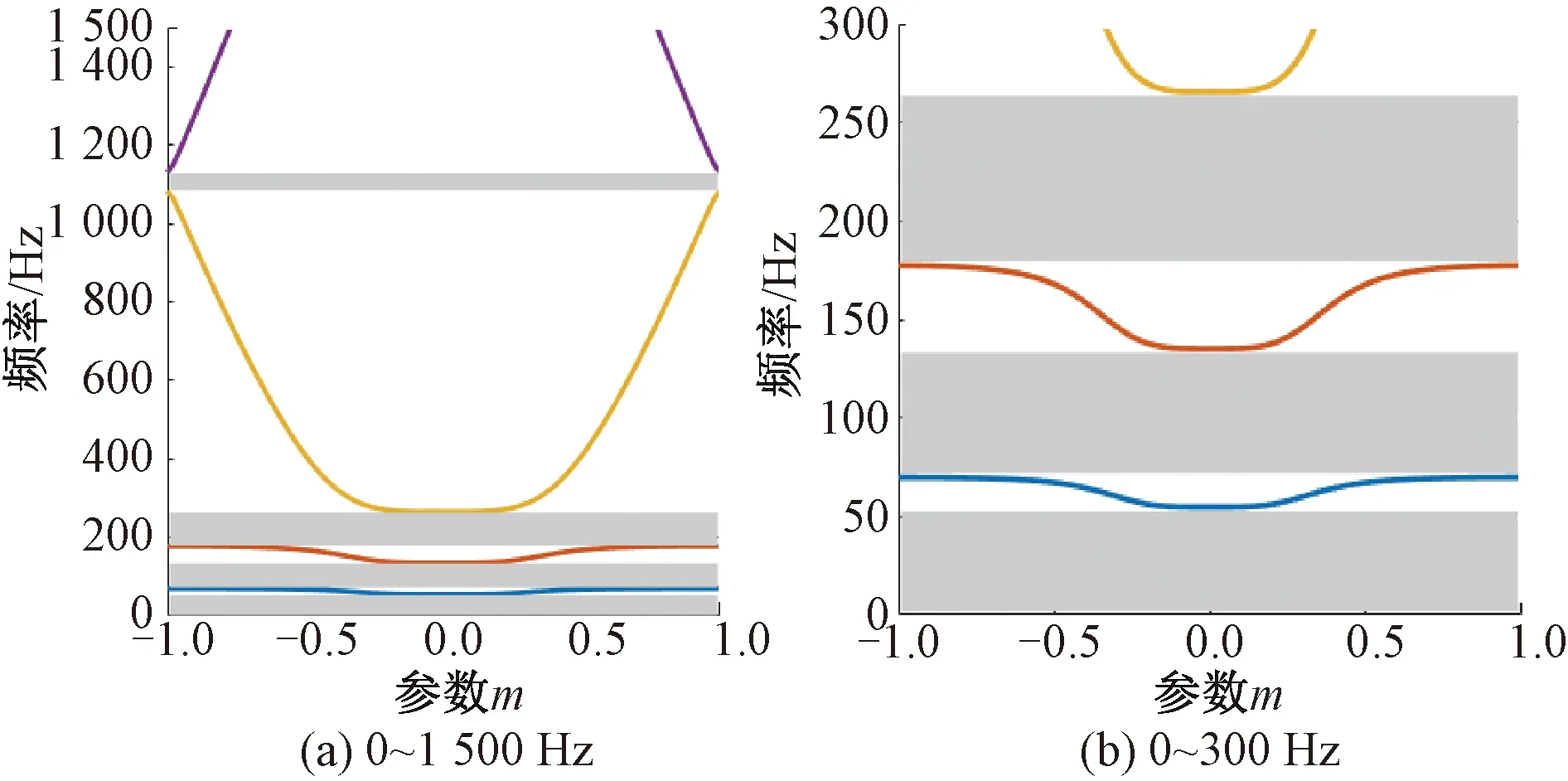
图2 周期性有砟轨道垂向振动带隙(混合法)

为了验证上述能量-平面波级数混合法计算周期性有砟轨道结构带隙特性的正确性，本文借助COMSOL Multiphysics多物理场仿真软件建立了相应的有限元模型并进行仿真分析。有限元模型中钢轨采用实体单元建模；轨枕与道床考虑为质量块；用连接弹簧模拟扣件垂向刚度以连接钢轨和轨枕；用连接弹簧模拟道床垂向刚度以连接轨枕和道床；用连接弹簧模拟路基垂向刚度以连接道床和路基。随后将上述模型进行单元划分，将单元设为Langrage-Quadratic型，出于求解精度的考虑，将其划分为16 544个域单元、6 888个边界元以及1 864个边单元，求解总自由度为86 832个。在钢轨两端添加Floquet周期性边界条件，并选择COMSOL软件中的固体力学模块进行求解，求解时间为23 min 8 s，从而得到周期性有砟轨道结构垂向振动带隙的有限元解，得到0～1 500 Hz内带隙结果见图3(a)，为便于对比分析，将其低频部分局部放大见图3(b)。

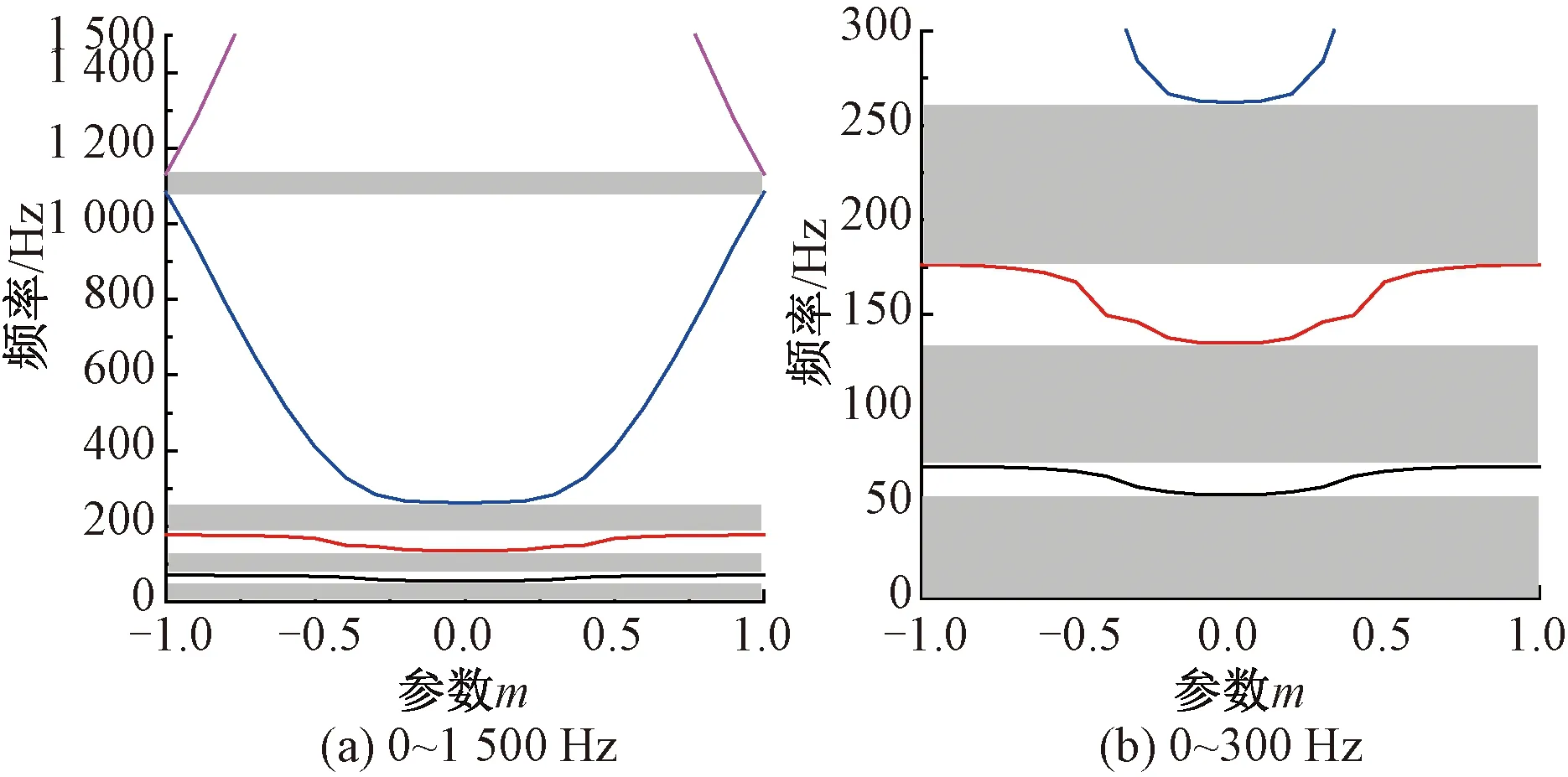
图3 周期性有砟轨道垂向振动带隙(有限元法)

将图2、图3中的带隙频率列表进行对比，见表2。

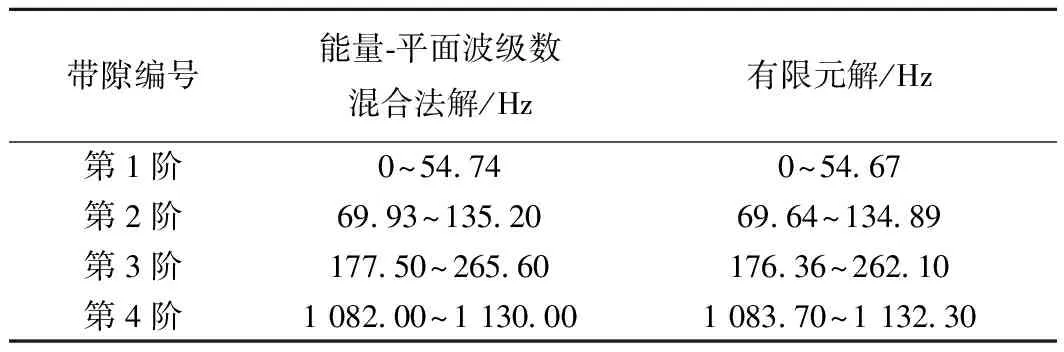
表2 能量-平面波级数混合法解与有限元解带隙频率对比

通过两种求解方式得到的带隙结果对比可以发现，能量-平面波级数混合法与有限元方法所求得的带隙基本一致，带隙频率范围与位置基本吻合，证明了能量-平面波级数混合法在求解周期性有砟轨道结构带隙特性方面的准确性。此外，混合法求解时间5.2 s远远小于有限元仿真计算时间23 min 8 s，说明混合法的计算效率较高。

3 影响因素分析

本节通过控制变量法，在保持其他参数不变的同时，分别改变扣件垂向刚度、道床垂向刚度和路基垂向刚度的值，研究它们对周期有砟轨道结构垂向振动带隙的影响。

3.1 扣件刚度的影响

仅改变扣件刚度，运用能量-平面波级数混合法分析周期性有砟轨道结构垂向振动前四阶带隙的变化情况，见图4。

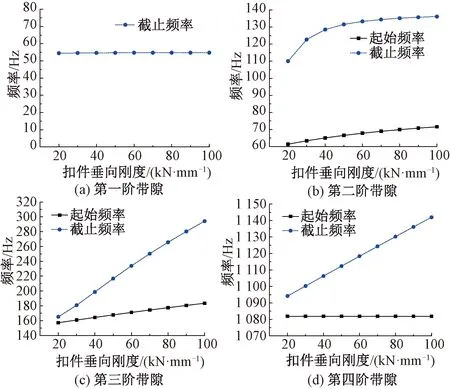
图4 扣件垂向刚度对垂向振动带隙的影响

由图4可知，当扣件刚度从20 kN/mm增加至100 kN/mm时，结构垂向振动0～1 500 Hz带隙中，第一阶带隙基本不受扣件刚度变化影响；第二、三阶带隙起始与截止频率均随扣件刚度的增大而增大，不同的是第二阶所受影响稍小，表现为第二阶带宽增加约16 Hz，第三阶带宽增加约102 Hz；第四阶带隙起始频率基本不受影响，而截止频率随扣件刚度增大而呈线性增大，表现为带宽增大约48 Hz。显然，第二、三和四阶带隙的特性均与扣件刚度相关。

3.2 道床刚度的影响

仅改变道床刚度，分析周期性有砟轨道结构垂向振动前四阶带隙的变化情况，见图5。

图5 道床垂向刚度对垂向振动带隙的影响

由图5可知，当道床刚度从60 kN/mm增加至140 kN/mm时，结构垂向振动0～1 500 Hz带隙中，仅第二阶带隙截止频率和第三阶带隙起始频率随道床垂向刚度的增大而呈线性增大，表现为第二阶带隙带宽增大约42 Hz，而第三阶带隙带宽减小约36 Hz，第一、四阶带隙不受影响。显然，第二、三阶带隙的特性均与道床刚度相关。

3.3 路基刚度的影响

仅改变路基刚度，分析周期性有砟轨道结构垂向振动前四阶带隙的变化情况见图6。

由图6可知，当路基刚度从60 kN/mm增加至140 kN/mm时，结构垂向振动0～1 500 Hz带隙中，仅第一阶截止频率和第二阶起始频率随路基垂向刚度的增大而呈线性增大，表现为第一阶带隙带宽增大约19 Hz，而第二阶带隙带宽减小约15 Hz，第三、四阶带隙基本不受影响。显然，第一、二阶带隙的特性均与路基刚度相关。

图6 路基垂向刚度对垂向振动带隙的影响

4 带隙形成机理分析

本文从0～1 500 Hz频率范围内选择出了四条带隙，并且这四条带隙均由Bragg带隙和局域共振带隙组成。其中，第四阶带隙为Bragg带隙，前三阶带隙为局域共振带隙。

已有文献研究表明[9]，Bragg带隙常出现在第n阶“pinned-pinned”频率处，并且该频率也是Bragg带隙的起始频率。根据“pinned-pinned”频率的特性可知，Bragg带隙的起始频率主要取决于扣件间距以及钢轨的物理参数，并且带隙宽度主要受扣件刚度的影响。由图4(d)可知，第四阶带隙的起始频率基本不受影响，但截止频率随扣件垂向刚度的增大而增大，表现为带宽增大；由图5(d)和图6(d)可知，第四阶带隙基本不受影响，从而验证了第四阶带隙为Bragg带隙。

局域共振带隙的形成主要是由钢轨和周期性排列的局域共振单元所引起。局域共振带隙的起始与截止频率所对应的振动模态可以用“质量-弹簧”模型来进行描述[13-15]。因此，为了进一步分析带隙中局域共振带隙的产生机理，本文建立了三层周期性有砟轨道结构用于带隙分析的“质量-弹簧”模型，见图7。

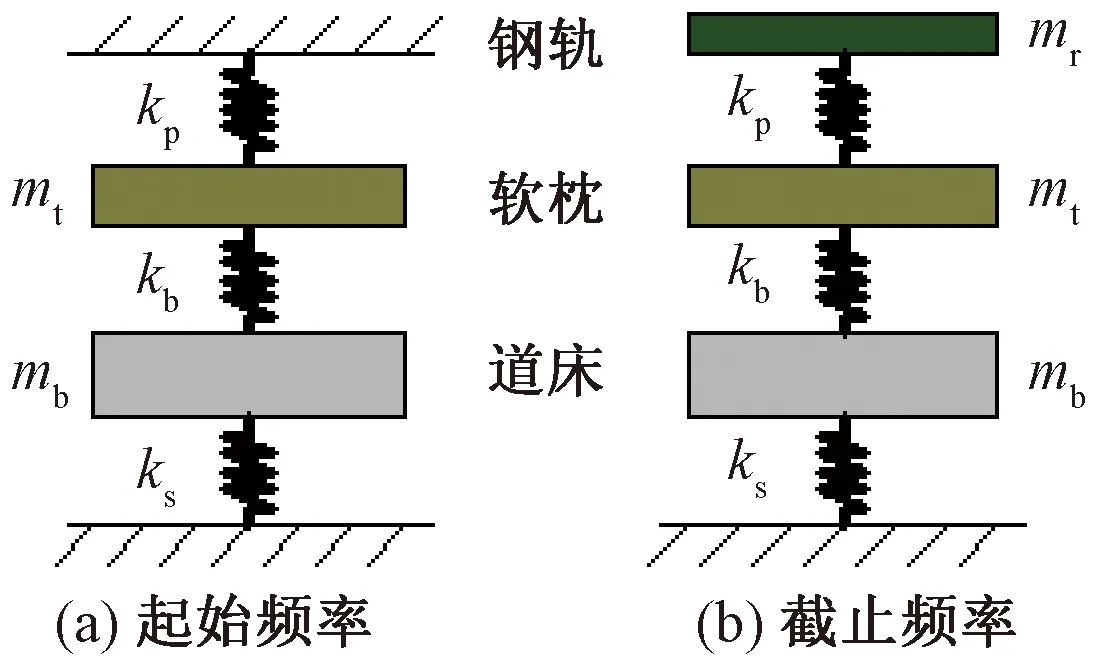
图7 周期性有砟轨道结构带隙分析集中质量模型

由图7(a)可得其特征频率ω满足如下关系式为

(35)

容易得到局域共振带隙的起始频率为

fs1=0

(36)

(37)

式中：ω1，ω2分别为式(35)的实数根；A1=(ks+kb)mt，A2=(kb+kp)mb。

由图7(b)可得其特征频率ω满足关系式

(38)

式(38)可化为

Aδ3+Bδ2+Cδ+D=0

(39)

式中：δ=ω2；A=-mbmtmr；B=mbmtkp+(ks+kb)mtmr+(kb+kp)mbmr；C=-kskpmt-kbkpmt-kbkpmb-kskbmr-kskpmr-kbkpmr；D=kskbkp；mr为钢轨质量且满足mr=ρrArl0。

容易得到局域共振带隙的截止频率为

(40)

式中：δ1,2,3为式(39)的三个正的实数根。

将表1中的各项参数代入式(37)和式(40)中，估算出结构局域共振带隙的起始频率为0、70.7、180.2 Hz；截止频率为54.7、135.3、267.8 Hz。从而估算得到结构局域共振带隙的频率范围为0～54.7 Hz，70.7～135.3 Hz，180.2～267.8 Hz。估算结果与表2中所列前三阶带隙结果基本一致，证明了前三阶带隙为局域共振带隙，并再次证明能量-平面波级数混合法求解轨道结构带隙特性的准确性。

结合第3节中所示的各个带隙频率随三种刚度的变化情况可知，第一阶局域共振带隙主要受路基刚度影响，第二、三阶局域共振带隙主要受道床刚度和扣件刚度影响。这是因为在周期性有砟轨道结构中，位于带隙范围内的低频弹性波无法沿轨道纵向传播，其中一部分直接传入路基中，另一部分则因局域共振而被限制在激振点附近的道床和轨枕中。

5 结论

本文基于能量变分原理及平面波级数展开，同时结合Bloch周期性原理，提出了一种用于求解三层周期性有砟轨道结构带隙特性的能量-平面波级数混合法，并且得到以下结论：

(1) 与现有的方法相比，基于能量变分原理的能量-平面波级数混合法计算量小，计算效率高，收敛性好，同时通过有限元法的验证可以证明能量-平面波级数混合法具有较高的准确性。

(2) 轨道结构在中低频范围内形成了三阶局域共振带隙，并且提高扣件、道床和路基刚度可以提高带隙频率和增大带宽。

(3) Bragg带隙主要受钢轨物理参数、扣件间距和刚度影响，且增大扣件刚度可以有效增大带宽。因此，可以通过合理设计轨道结构参数来调控弹性波的传播。

(4) 在周期性有砟轨道结构中，位于带隙范围内的低频弹性波无法沿轨道纵向传播，其中一部分直接传入路基中，另一部分则因局域共振而被限制在激振点附近的道床和轨枕中。