考虑荷载相互作用的非线性时变疲劳可靠性分析
高 凯,刘 纲,蒋 伟
(1.重庆大学 土木工程学院, 重庆 400045;2.重庆大学 山地城镇建设与新技术教育部重点实验室, 重庆 400045;3.重庆渝富产城运营建设发展有限公司,重庆 401121)
疲劳可靠度是指产品在规定时间内完成预期功能而不发生故障的概率。从20世纪80年代以来,载荷-强度干扰可靠度模型被大量应用于构件或系统疲劳可靠性评估中,但该模型仅能考虑静态可靠度,不适用于复杂动态系统的可靠度分析。这主要是因为受强度退化、荷载变化和荷载累积效应等影响,构件的强度和应力关系一直处于变化状态,构件或系统的可靠度将随时间及荷载作用次数的变化而发生改变,属于时变可靠度范畴[1]。而考虑疲劳损伤累积的可靠性建模方法能考虑载荷时变历程,较好反映结构时变特性,更符合工程实际,所以近年来该类方法已逐渐成为可靠度分析中的常用方法[2]。
疲劳损伤累积模型可以分为线性和非线性累积模型,其中Miner线性模型因其原理和规则简单,在实际工程中得到了广泛应用[3-4]。但在分析变幅荷载作用时,该模型忽略了荷载加载顺序和不同荷载相互作用等因素对疲劳损伤累积的影响,这与实际情况不符。因此,在变幅作用时,该模型的可靠度计算精度不尽如人意[5]。为此,诸多学者利用损伤曲线法、能量法、材料物理性能退化法、连续损伤力学法等非线性损伤累积理论建立疲劳可靠度状态方程[6]。
在非线性累积损伤模型中,文献[7]基于损伤曲线理论,在有效裂纹增长长度和损伤等效的基础上,提出了Manson-Halford(M-H)非线性疲劳损伤累积模型,该模型能处理复杂加载历史下的疲劳损伤,可较好反映结构疲劳损伤随荷载作用次数的变化趋势,且模型参数较少,故适用于非线性损伤分析。文献[8]采用M-H模型成功分析了焊接接头的疲劳特性,并与Miner模型结果进行对比分析,表明M-H模型可用于工程设计。文献[9-10]结合M-H模型和剩余强度退化模型,建立时变疲劳可靠度分析方法,并用两组试验数据进行验证,所得计算结果和试验数据吻合较好。文献[11]利用M-H模型预测了二级和多级荷载作用下构件的疲劳寿命。
应该指出的是,该模型未考虑载荷间的相互作用,其在分析多级载荷作用下的疲劳可靠度时易出现较大误差[12]。另一方面,目前非线性时变疲劳可靠度计算主要采用一次二阶矩法(FOSM)、Monte Carlo法(MCS)等传统方法[13]。但FOSM存在非线性状态方程适应差、忽略高阶项导致计算误差大等问题;MCS存在计算量大、计算效率低等不足,特别是在考虑时变可靠度计算时,其计算效率较低[14]。而近十几年提出的概率密度演化方法(PDEM)在分析可靠度时,对非线性问题有较好的适应性,且计算精度和效率较高[15-16]。
为此,针对M-H模型未考虑荷载相互作用的问题,本文通过荷载幅值对数平方比率指数项计入多幅级载荷的相互作用,提出M-H改进模型,结合改进M-H模型和概率密度演化方程,建立考虑非线性疲劳累积损伤的动态可靠度分析方法;采用标准45钢和螺旋压缩弹簧试验验证所提方法的适用性和准确性。
1 非线性疲劳损伤累积模型
1.1 M-H损伤累积模型
在M-H模型中,构件在应力σi作用下循环ni次的疲劳损伤累积量D为
( 1 )
式中:a0为ni=0时构件的初始裂纹长度;Nfi为构件在应力σi作用下失效的循环次数,即疲劳寿命;B和β为与材料特性相关的参数。构件在初始状态下的裂纹长度a0一般较小,可忽略不计,故通常a0=0[17],因此式( 1 )可改写为
( 2 )
式( 2 )反映了常幅荷载作用下疲劳损伤累积量,即M-H模型。在常幅荷载σ1、σ2、σ3分别作用下的疲劳损伤曲线如图1所示。
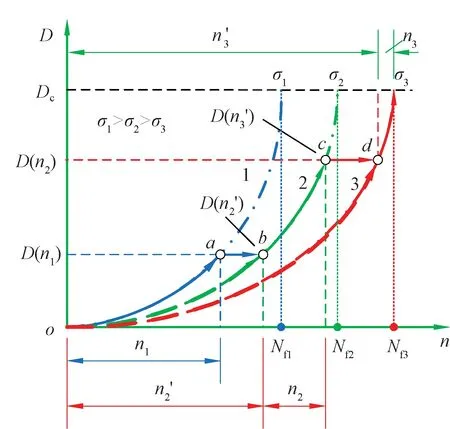
图1 三级应力加载下疲劳损伤累积量
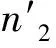
( 3 )
式中:n2′为载荷σ2产生与载荷σ1作用n1次循环相同损伤的等效循环次数。式( 3 )可改写为
( 4 )
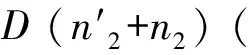
( 5 )
以此类推,可以得到三级荷载同时加载下的疲劳累积损伤模型为
( 6 )
式中:n3′为荷载σ3产生与前两级荷载σ1、σ2作用n1+n2次循环相同损伤的等效循环次数。
1.2 改进的M-H疲劳累积模型
通过式( 6 )可知,多级荷载作用下M-H损伤累积模型仅考虑荷载序列影响,忽略了不同幅级荷载间的相互作用影响。而业界提出通过在荷载循环次数n上引入与荷载水平相关的指数项来解决这一问题[18],从而更准确反映多幅级荷载作用下疲劳累积损伤。借鉴该思路,本文通过引入荷载幅值对数平方比率来考虑荷载间的相互作用影响,即在两级载荷作用时的损伤等效转换过程中,增加荷载幅值对数平方比率指数项,即将式( 4 )改写为
( 7 )
将式( 7 )代入式( 5 ),得到两级不同幅值加载下考虑荷载相互作用的疲劳累积损伤为
( 8 )
若考虑第三级荷载作用,根据损伤等效原理,可将前二级累积损伤量D(n1+n2)转换为第三级荷载循环作用n3′次的损伤量D(n3′)。再根据式( 7 )同时考虑荷载加载顺序和荷载相互作用的影响,则前两级荷载损伤产生的等效循环次数比可表示为
( 9 )
将式( 9 )代入式( 6 ),得到考虑荷载加载顺序和相互作用时三级加载疲劳累积损伤为
(10)
依次类推,考虑荷载相互作用的前k-1级加载损伤可等效为第k级加载作用nk′次后的损伤。
(11)
考虑荷载加载顺序和相互作用的k级加载疲劳累积损伤为
(12)
在M-H模型的基础上,通过引入荷载幅值对数平方比指数考虑各幅级荷载间的相互作用,提出改进M-H模型。
2 基于PDEM的时变可靠度分析法
可靠度分析包含两大步骤:建立结构极限状态函数和可靠度计算。根据改进M-H模型建立多级载荷作用下非线性疲劳可靠度分析的状态函数;利用概率密度守恒原理建立基于状态函数的概率密度演化方程;利用数值求解方法对演化方程进行求解,获取结构的时变疲劳可靠度曲线。
2.1 疲劳可靠度分析的极限状态函数
疲劳可靠度分析的极限状态函数G可表示为
(13)
式中:Dc为疲劳损伤阈值,一般取1[19];n为循环次数;k为多级荷载幅值的数量。当G(n)>0时,表示结构疲劳累积损伤未达到极限值,处于安全状态;当G(n)=0时,结构处于疲劳极限状态。从式(12)和式(13)可知,疲劳极限状态方程中只有不同应力幅下疲劳寿命Nfi是随机变量,在多幅级荷载作用过程中没有新随机源产生,因此系统是一个概率保守系统[20]。为此,可根据概率守恒原理构建疲劳极限状态函数的概率密度演化方程。
2.2 疲劳状态函数的概率密度演化方程
基于概率守恒原理,随机事件的概率密度函数随时间演化的规律可表示为[21]
(14)
式中:Z为感兴趣的物理量(如应力、弯矩、疲劳损伤、变形等);Θ为影响物理量变化的随机变量;θ为随机变量Θ的子集;pZΘ(z,θ,t)为增广系统(Z,Θ)的联合概率密度函数;ΩZ×ΩΘ为增广系统的空间。式(14)经数学处理和变换可以得到增广系统的广义概率密度演化方程为
(15)
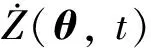
疲劳可靠度分析感兴趣的物理量是疲劳损伤,故将式(15)中的物理量Z用疲劳损伤状态值G替换,而疲劳损伤状态值G是一个与循环次数n有关的函数,循环次数n随荷载作用从0开始逐步、连续增长,具有时间特性,故可用循环次数n替换时间t,式(15)可改写为
(16)
式中:g为疲劳损伤状态值G中的一个元素。式(16)在初始时刻n=0的初始条件为
pGΘ(g,θ,n)|n=0=δ(g-g0)PΘ(θ)
(17)
式中:δ为Dirac函数
(3)CDFU占地面积小,放置灵活,运行稳定,气源既可以选择N 2又可以利用平台天然气,对海上平台适应性强。
联合式(13)、式(17)对式(16)进行求解,并在随机变量空间ΩΘ上积分,得到疲劳损伤随时间变化的概率密度函数为
(18)
通过M-H模型建立的概率密度演化方程涉及的随机变量类型较少,求解过程人为影响因素较少,适用于时变疲劳可靠度分析。
2.3 疲劳概率密度演化方程的数值求解流程
式(16)的解析解较难获得,本文采用PDEM数值方法进行求解,具体计算步骤如下:
Step1代表点的选择。利用数论选点法[22]在随机变量空间ΩΘ内选择nsel个有效代表点,并将空间ΩΘ离散为nsel个子空间,再对子空间进行积分,得到每个代表点的赋得概率Pq(q=1, 2, …,nsel)。
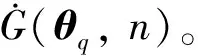
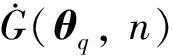
Step4概率密度的积分求解。利用式(18)积分,获得随荷载循环次数变化的概率密度函数。
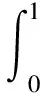
(19)
3 算例分析
为验证改进M-H模型和PDEM可靠度计算方法,利用已有材料疲劳数据,验证所提模型预测疲劳寿命精度;通过两个时变疲劳可靠度分析算例,验证所提改进M-H模型和可靠度分析方法的有效性。
3.1 疲劳剩余寿命预测
为验证改进M-H模型在多幅级荷载作用下的合理性,以30CrMnSiA、铝合金6082T6和动车铝合金三种材料的试验数据为对象[23-24],对比Miner模型、M-H模型及改进M-H模型对材料剩余寿命的预测精度。材料参数B=2/3,β=0.4,结合试验数据,Miner模型、M-H模型和改进M-H模型的计算结果见表1~表3。
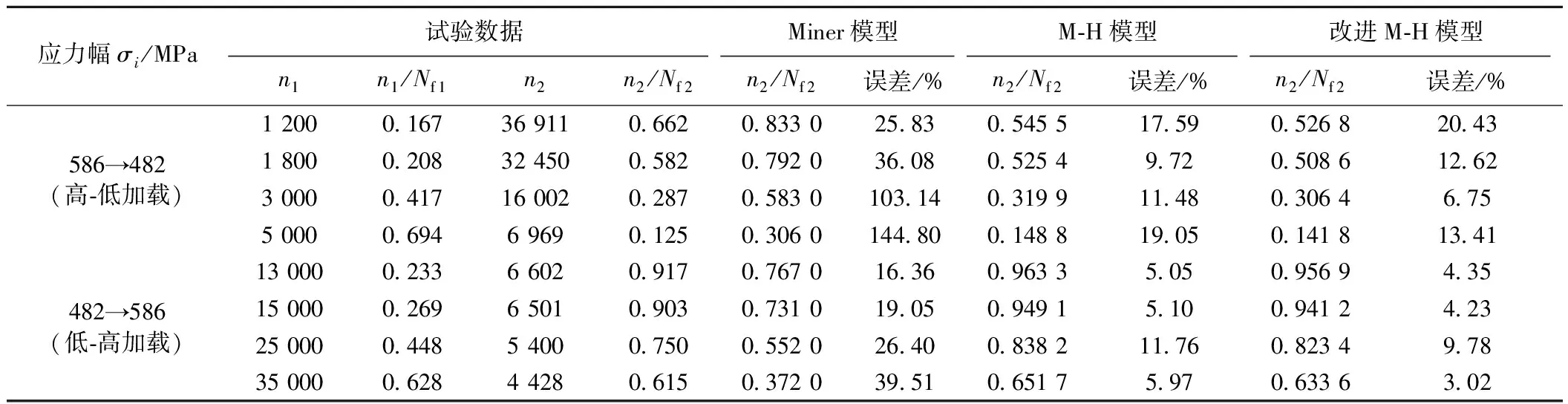
表1 两幅级荷载下30CrMnSiA试验数据及剩余寿命预测结果
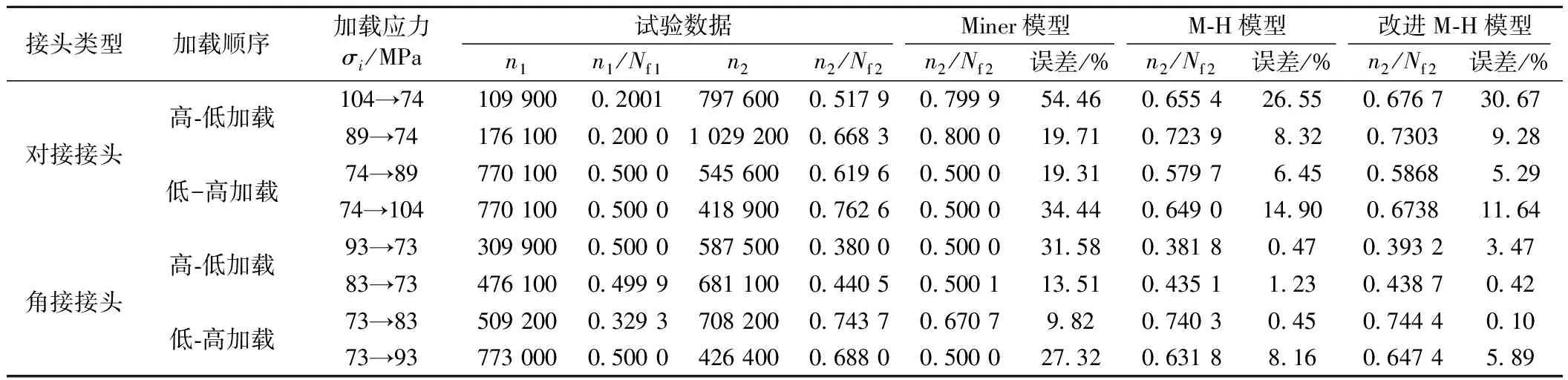
表2 两幅级荷载下动车铝合金焊接接头试验数据及剩余寿命预测结果
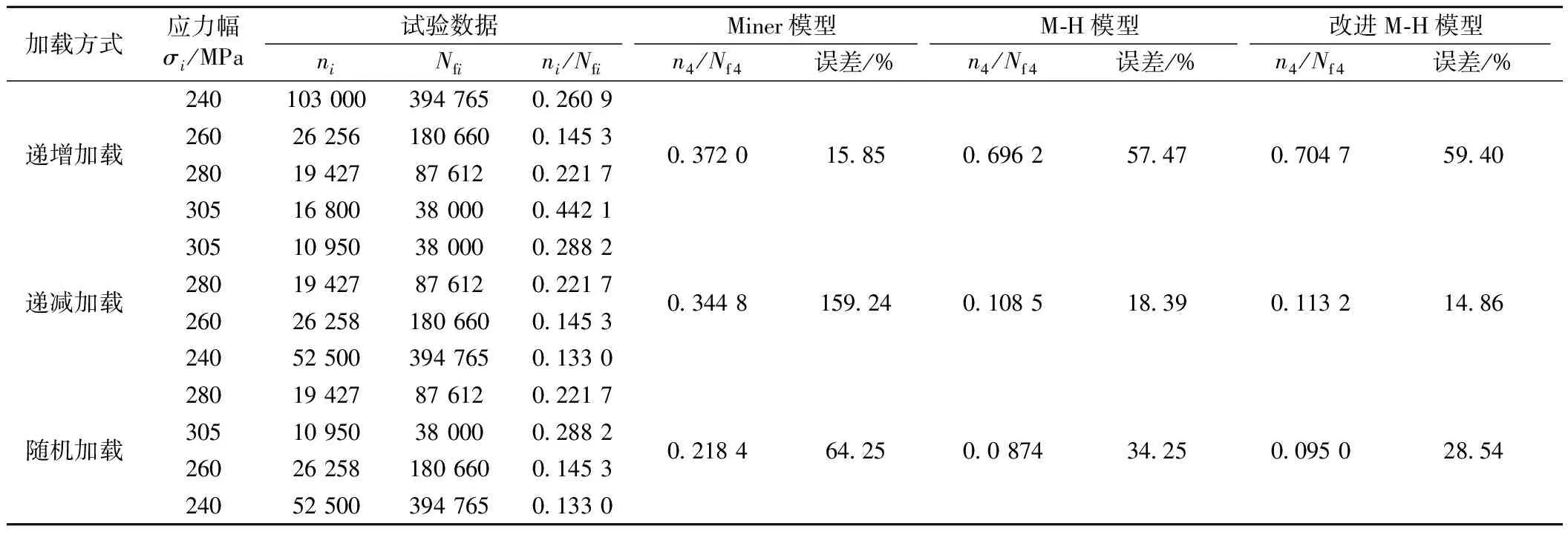
表3 四幅级荷载下铝合金6082T6试验数据及剩余寿命预测结果
从表1、表2可知,两幅级荷载作用下M-H模型和改进M-H模型的预测精度较Miner模型高,且改进M-H模型的预测结果好于M-H模型;在动车铝合金焊接接头试验中,改进M-H模型的预测精度远高于Miner模型和M-H模型;从表3可知,在铝合金6082T6四幅级加载实验中,改进M-H模型的预测精度强于Miner模型和M-H模型。因此,通过不同材料、不同幅级荷载作用下试验数据分析可知,改进M-H模型预测结果与试验数据更相符,其精度优于传统Miner模型和M-H模型。
3.2 PDEM时变疲劳可靠度分析
(1)标准45钢时变疲劳可靠度分析
文献[25]针对标准45钢在三种恒幅荷载(366、331、309 MPa)的疲劳试验数据进行统计,得出三种恒幅荷载对应的疲劳寿命Nf服从正态分布:Nf1~N(45 027,9 917),Nf2~N(151 422,52 286),Nf3~N(658 944, 209 045)。利用改进M-H模型和PDEM可靠度分析方法对两幅级循环荷载(高低(H-L)331 MPa→309 MPa、低高(L-H)331 MPa→366 MPa)的试验数据进行时变疲劳可靠度分析。同时,将Miner、M-H模型和PDEM可靠度方法相结合,进行时变可靠度对比分析,结果如图2、表4、表5所示。
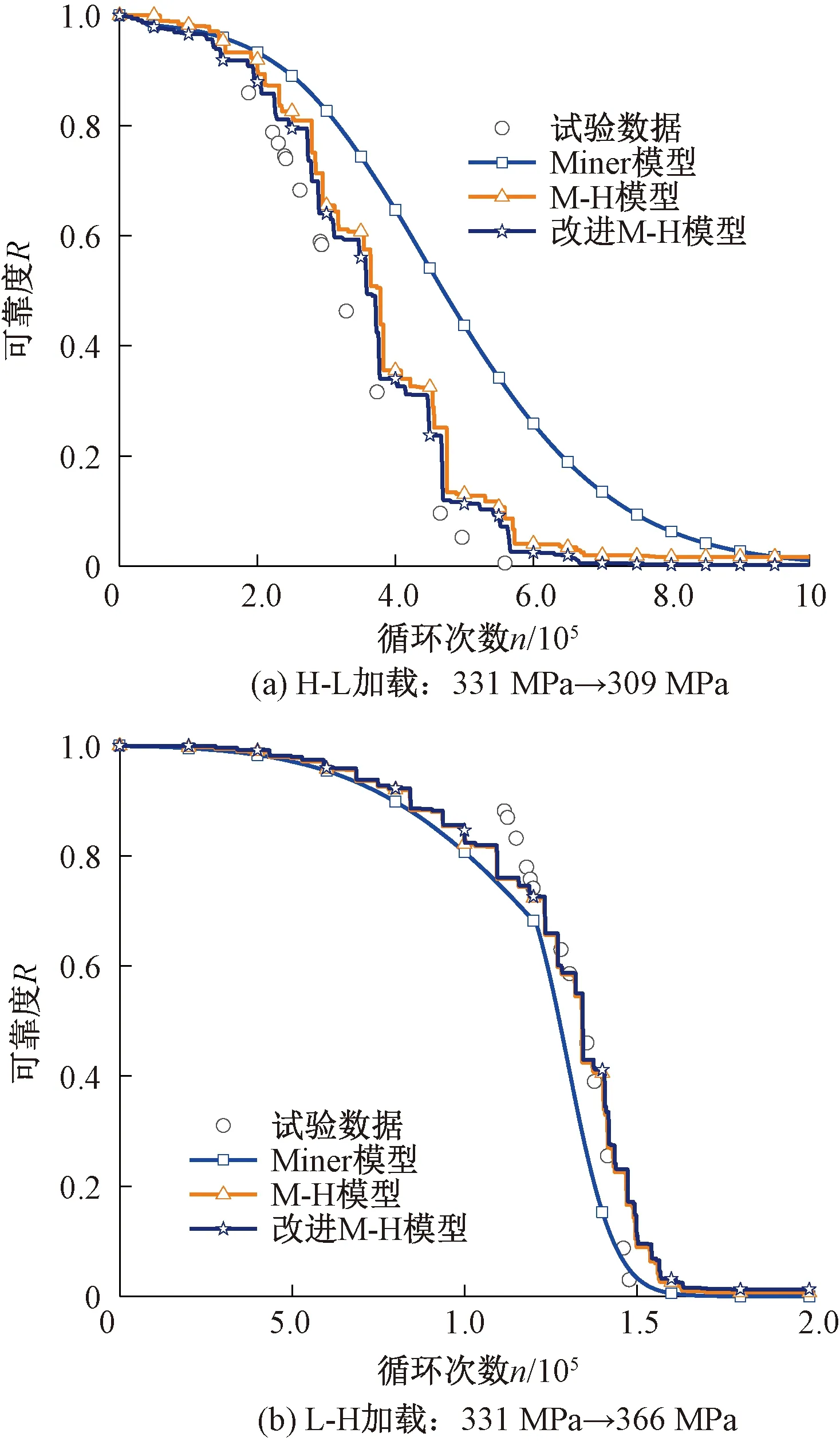
图2 不同加载方式下标准45钢时变疲劳可靠度曲线
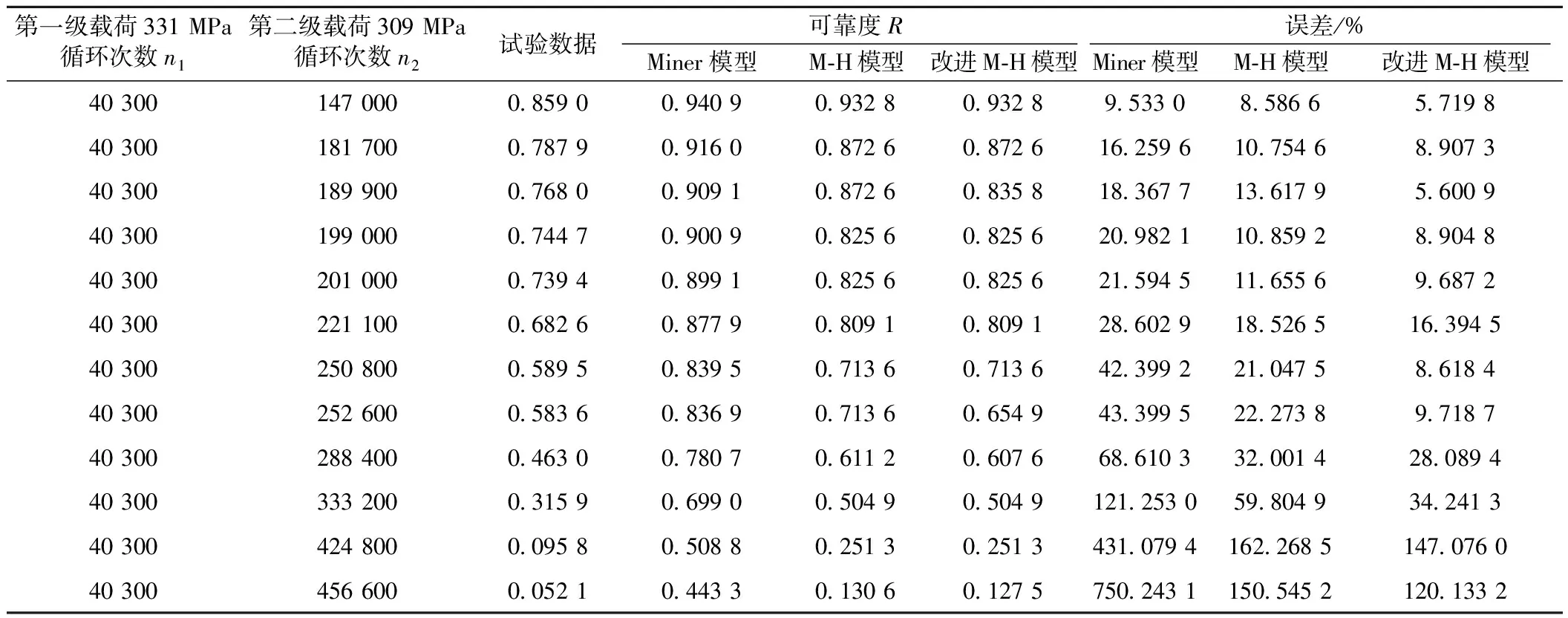
表4 H-L工况下标准45钢时变疲劳可靠度计算对比
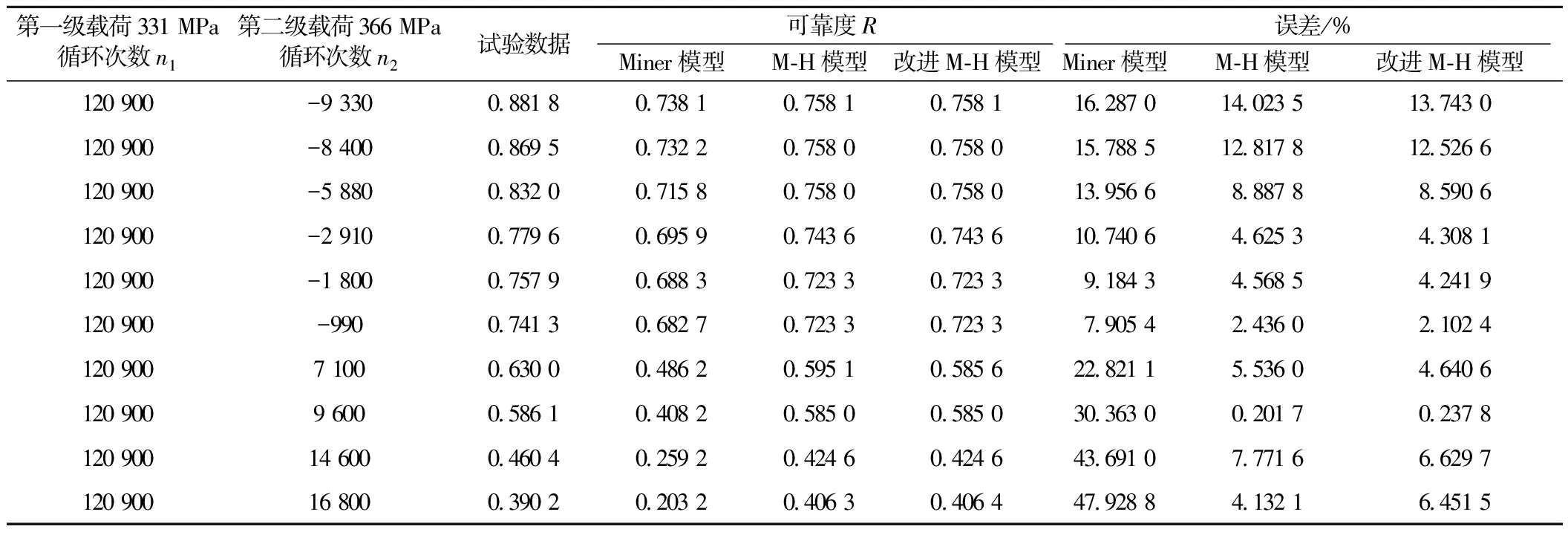
表5 L-H工况下标准45钢时变疲劳可靠度计算对比
从图2可知,在两级加载作用时,M-H模型和改进M-H模型得到的时变疲劳可靠度曲线与试验数据拟合较好,而Miner线性模型效果较差,表明改进M-H模型和可靠度计算方法能较好应用于构件时变疲劳可靠度计算。从表4、表5可知,改进M-H模型所得可靠度值与试验数据误差最小,这主要因为该模型考虑了载荷次序效应和载荷间相互作用效应,可得到更高的计算精度。
(2)螺旋压缩弹簧时变疲劳可靠度分析
为进一步验证所提PDEM可靠度分析法的准确性,针对Zaccone开展的螺旋压缩弹簧疲劳试验进行分析[26]。该试验采用三级荷载高低(H-L)加载:435 MPa→360 MPa→320 MPa和三级荷载低高(L-H)加载:320 MPa→360 MPa→435 MPa。三种恒幅荷载的疲劳寿命Nf服从正态分布,其统计特征从高至低分别为:Nf1~N(64 616,9 692)、Nf2~N(320 222,53 947)、Nf3~N(867 130,156 303)。为对比PDEM方法的计算精度,将改进M-H模型与常用FOSM和MCS结合进行时变可靠度计算,并用MCS计算结果作为参考,使用2范数相对误差指标进行评价。
(20)
式中:R(n)代表PDEM或FOSM法得到的时变疲劳可靠度曲线;RMCS(n)代表由MCS计算得到的时变可靠度曲线。计算结果如表6和图3所示。

表6 不同可靠度分析方法与MCS的相对误差
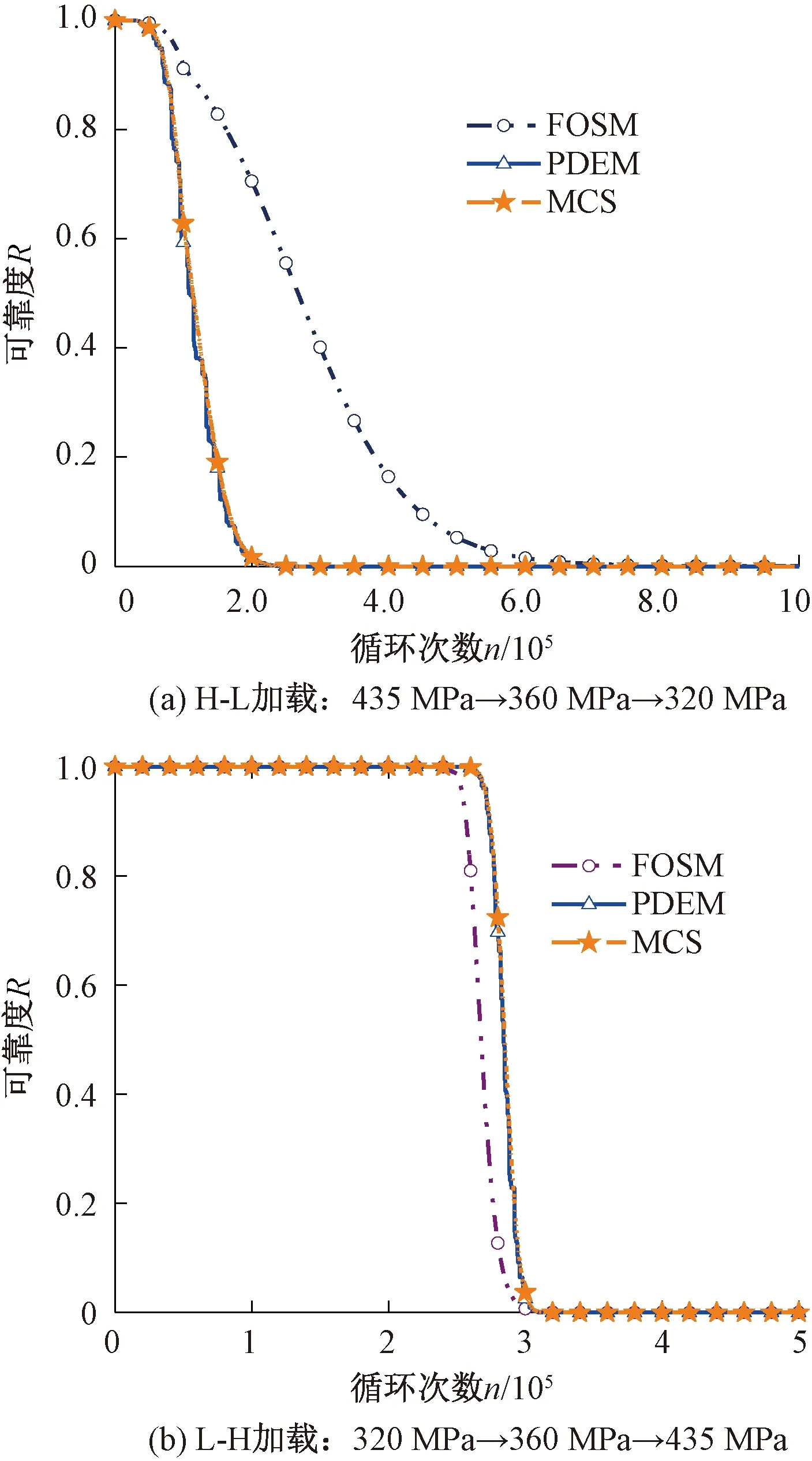
图3 不同疲劳可靠度分析方法在多级荷载作用下的比较
从表6和图3可知,在H-L加载和L-H加载工况下,PDEM法计算的时变疲劳可靠度曲线与MCS法所得曲线拟合更好,且相对误差较小,表明在时变疲劳可靠度分析时具有较高精度。应该指出的是,在同一台个人计算机上,MCS法的计算时间为14 456 s,而PDEM方法的计算时间仅为726 s,PDEM方法的计算时间约为MCS法的1/20。
4 结论
针对非线性时变疲劳可靠度在多幅级加载下计算精度低、传统时变疲劳可靠度方法计算效率不高的问题,通过改进M-H模型考虑荷载相互作用对疲劳损伤的影响,基于概率密度演化理论建立PDEM时变疲劳可靠度分析方法,并通过疲劳试验验证所提方法的适用性,得到如下结论:
(1)基于M-H理论提出可同时考虑加载顺序和相互作用影响的非线性疲劳损伤累积模型,与Miner模型和M-H模型相比,所提改进M-H模型能更好表征疲劳损伤演变特征,更适合用于剩余疲劳寿命预测。
(2)基于改进M-H模型和概率密度演化理论,建立PDEM非线性时变疲劳可靠度分析方法,与传统可靠度分析方法相比,所需的随机变量类型少,人为影响小。
(3)通过实验算例表明,改进M-H模型和PDEM可靠度分析方法计算精度好于Miner模型和原M-H模型,且计算效率是MCS法的20倍。为此,在多幅级加载情况下,所提改进M-H模型和PDEM可靠度分析方法计算效率快、精度高,可更好适应实际工程的需求。

