基于Copula函数的列车定位惯性单元剩余寿命预测方法
上官伟,巴明明,孟月月
(1.北京交通大学 电子信息工程学院, 北京 100044;2.北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044;3.北京市电磁兼容与卫星导航工程技术研究中心, 北京 100044)
高速铁路的快速发展,对列车定位技术提出了更高的要求。基于全球卫星导航系统(Global Navigation Satellite System, GNSS)和惯性测量单元(Inertial Measurement Unit, IMU)的列车组合定位方式,可以实现列车动态的精准定位,保障列车定位的连续性、自主性,减少列车定位对轨道电路和应答器等地面设备的依赖,降低铁路建设投入以及运营维护成本,是列车定位技术未来的重要发展方向[1]。作为其中的关键设备,确保组合定位系统中IMU在服役期间的工作性能,对保障系统的定位精度和运行可靠性十分重要。列车定位惯性单元(以下简称“惯性单元”)是高集成度、高可靠性的捷联式惯性导航系统,主要由惯性传感器和电子部件组成。捷联式惯性导航系统直接固定在运载体上,其中精密部件惯性传感器直接承受高速列车的振动、冲击以及角运动。随着运行时间的积累,惯性单元的性能会发生退化,当退化达到一定程度时,测量系统不再满足列车定位精度的要求,意味着惯性单元的有效使用寿命也随之终结。
针对上述问题,国内外开展了大量关于惯性导航系统的寿命预测研究,主要通过设备的性能退化数据,评估、预测设备服役期间的健康状态或剩余使用寿命(Remaining Useful Life, RUL)。设备性能评价指标是实现RUL精确预测的重要基础。现有的数据驱动RUL预测方法[2],从采用不同元数性能参量的角度可分为单性能参量和多元性能参量两大类。
单性能指标的RUL预测方法极其丰富,根据目标设备自身性能表征特点、性能数据采集的条件以及工程需求不同,进行RUL预测的思路也会不同。Huang等[3]利用状态空间刻画一个带自适应漂移的非线性Wiener过程模型,推导了退化漂移状态条件下RUL预测的显示表达式。王瑞峰等[4]建立基于Gamma退化过程的状态空间模型,采用EM-PF算法估计模型参数,并据此求得RUL的概率密度和分布函数。Lei等[5]提出一种基于Wiener过程且考虑四源不确定性的随机性能模型,通过离线数据与在线数据的联合估计,实时获得轴承的剩余寿命。Wang等[6]进一步利用一个基于多隐状态带非线性漂移的扩散过程,进行可充电电池RUL的预测。
目前针对具有多性能评价指标的复杂设备,进行健康状态评估、RUL预测的方法主要有两种途径: ①采用数据融合的技术,先将多元性能参数信息融合后进行单特征的提取,再采用单性能参量的RUL预测方法;②直接对现有性能退化模型或者RUL预测模型进行扩展,采用相关性描述技术,准确、有效建立多元性能参量间的关系,确保RUL预测的精度。金晓航等[7]针对轴承具有二元性能指标,提出一种基于二元维纳过程的RUL预测方法,并利用AIC准则选择Copula函数进行描述两个性能指标间的相关性。Hao等[8]针对LED灯的二元性能参量采用二元非线性扩散过程构建退化模型,并基于Copula函数描述二元性能参量的依赖关系,利用蒙特卡洛(MCMC)算法进行参数估计,实现退化设备的可靠性评估。Peng等[9]提出一种基于逆Gaussian的二元退化模型,采用Copula函数建立联合分布,并利用两阶段贝叶斯方法进行退化过程和Copula函数参数估计。
针对惯性单元的RUL预测是对其进行健康管理、维修维护时,所需的重要健康状态评估信息。纵观当前PHM领域技术的研究重点可知,RUL预测的关键是如何考虑预测的不确定性因素,建立合理的性能退化模型,获得RUL的概率密度分布并提高RUL预测精度。周源等[10]采用加速度计的零位电压百分比增量作为加速度计的性能退化参数,基于逆Gaussian过程建立性能退化模型,实现加速度计的剩余寿命预测。Miao等[11]针对惯性器件陀螺仪提出一种小波分析和SVM结合的方法,采用小波分析进行陀螺仪性能数据的预处理,利用SVM对处理后的数据进行建模,实现陀螺仪的剩余寿命预测。滕飞等[12]以加速度计加速退化数据为对象,提出了一种较为客观、实用的加速退化数据统计分析方法,其特点是基于加速因子不变原则进行加速退化数据建模,结合 Matlab软件中的相关函数实现参数估计及可靠寿命预测。
根据上述文献研究现状,提出一种列车定位惯性单元的RUL自适应预测研究方法。首先,从IMU结构组成和功能性质角度出发,选取惯性传感器陀螺仪和加速度计的随机误差指标评价设备性能状态,构建IMU的性能评价指标体系。其次,采用具有普适性的非线性漂移维纳过程建立性能指标退化模型。基于首达时间概念获取RUL的概率密度函数(Probability Density Function,PDF),在此基础上,利用Copula理论描述二元性能指标间的动态相关性,建立二元性能退化模型及RUL的联合分布。再次,根据参数分步估计的思想,先对退化模型参数利用期望最大化(Expectation Maximization, EM)和Rauch-Tung-Striebel(RTS)后向平滑联合算法,实现退化模型参数的实时自适应估计;再利用极大似然估计(Maximum Likelihood Estimation, MLE)算法更新Copula函数的相关性参数。最后,通过对比预测结果,证明本文提出的RUL预测方法可以有效减小预测的不确定性、提高预测精度。
1 列车定位惯性单元的性能指标选取
作为列控系统的重要装备,列车定位单元普遍使用基于GNSS和IMU的组合定位方式,其结构见图1。IMU作为其中的重要组成部分,对其开展基于性能状态的寿命预测具有重要意义。惯性单元性能的主要评价标准是测量信息的精准度。近年来,中国学者结合实际应用,普遍采用随机漂移中的随机游走系数作为惯性器件的性能评价指标[13]。
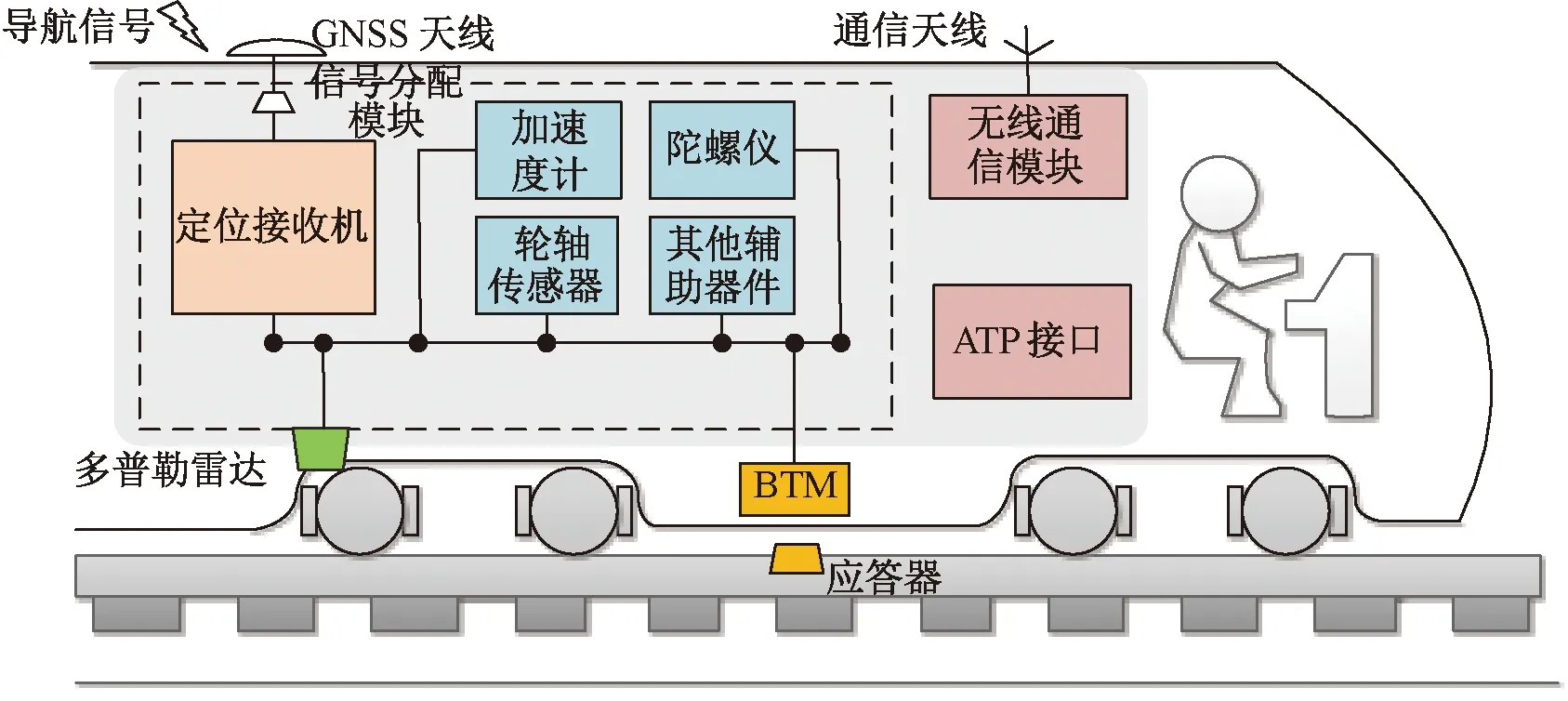
图1 基于GNSS和IMU组合的列车定位系统结构
本文的研究对象为实验室自主研发的列车定位系统中所采用的微机电型惯性测量单元(MEMS-IMU)。该型号惯性单元的产品标准规格说明中,明确标明随机游走系数是该型号惯性单元内MEMS惯性器件的主要性能指标。因此,本文针对列车定位惯性单元的性能指标体系为加速度计的速率随机游走系数和陀螺仪的角度随机游走系数。
本文用于研究验证的数据是对目标惯性单元失效前近2年服役过程中周期性监测得到的测量数据。根据实验需求和实际应用安排,针对目标惯性单元每7 d作为一个采样间隔进行性能监测。在相同的采集条件下,性能监测采集周期共计85周,总计85组性能退化数据。
高速列车具有沿轨道水平运动的特点,根据列车定位系统车内实验的安装方式,可知惯性单元的主要敏感轴为x轴与y轴。
针对目标惯性单元退化周期内的监测数据,采用Allan方差法[14]对敏感方向上惯性器件的测量数据进行性能指标辨识,所得每个监测点的性能退化量见图2。
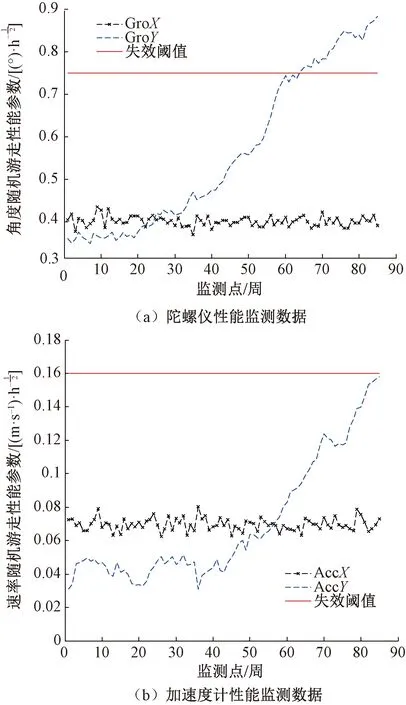
图2 IMU关键部件性能监测数据
由图2可知,沿敏感方向y轴的惯性传感器,监测获得的性能指标参数具有明显的退化趋势。因此,为有效评估设备的健康状态,列车定位惯性单元的性能评价指标参数为y轴加速度计和陀螺仪的随机游走系数。
根据列车定位系统的精度指标要求,结合实验室列车组合定位系统中目标惯性设备的性能指标评价体系,惯性单元性能的失效阈值设定情况如表1所示。
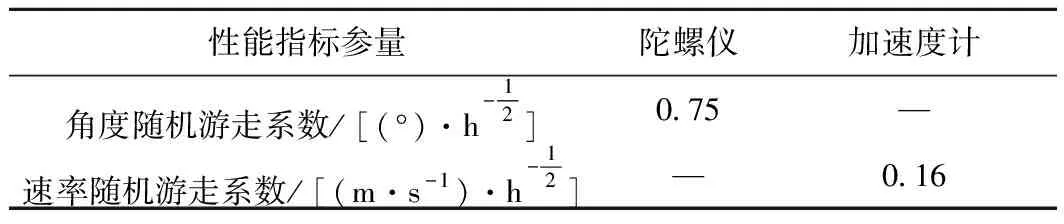
表1 惯性单元性能指标的失效阈值
2 基于Copula函数的惯性单元剩余寿命建模方法
2.1 单性能参量的剩余寿命建模
2.1.1 单性能参量的性能退化模型
由第1节可知,列车定位惯性单元的性能状态可由陀螺仪和加速度计的性能指标共同表征,且两种惯性器件的退化监测数据均呈现非单调、连续波动的特点,表明单部件的性能退化过程具有明显的随机性和时变不确定性。对此本节将基于具有一般性带有非线性漂移Wiener过程进行单部件的性能退化建模。
假设单部件的性能退化过程为{X(t),t≥0},基于带非线性漂移Wiener过程建立的性能退化模型为
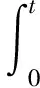
( 1 )
性能退化轨迹的个体差异性见图3。由图3可以看出,实际退化过程中,设备性能状态退化估计,不仅和当前时刻的性能退化量相关,而且依赖于设备历史性能退化轨迹。
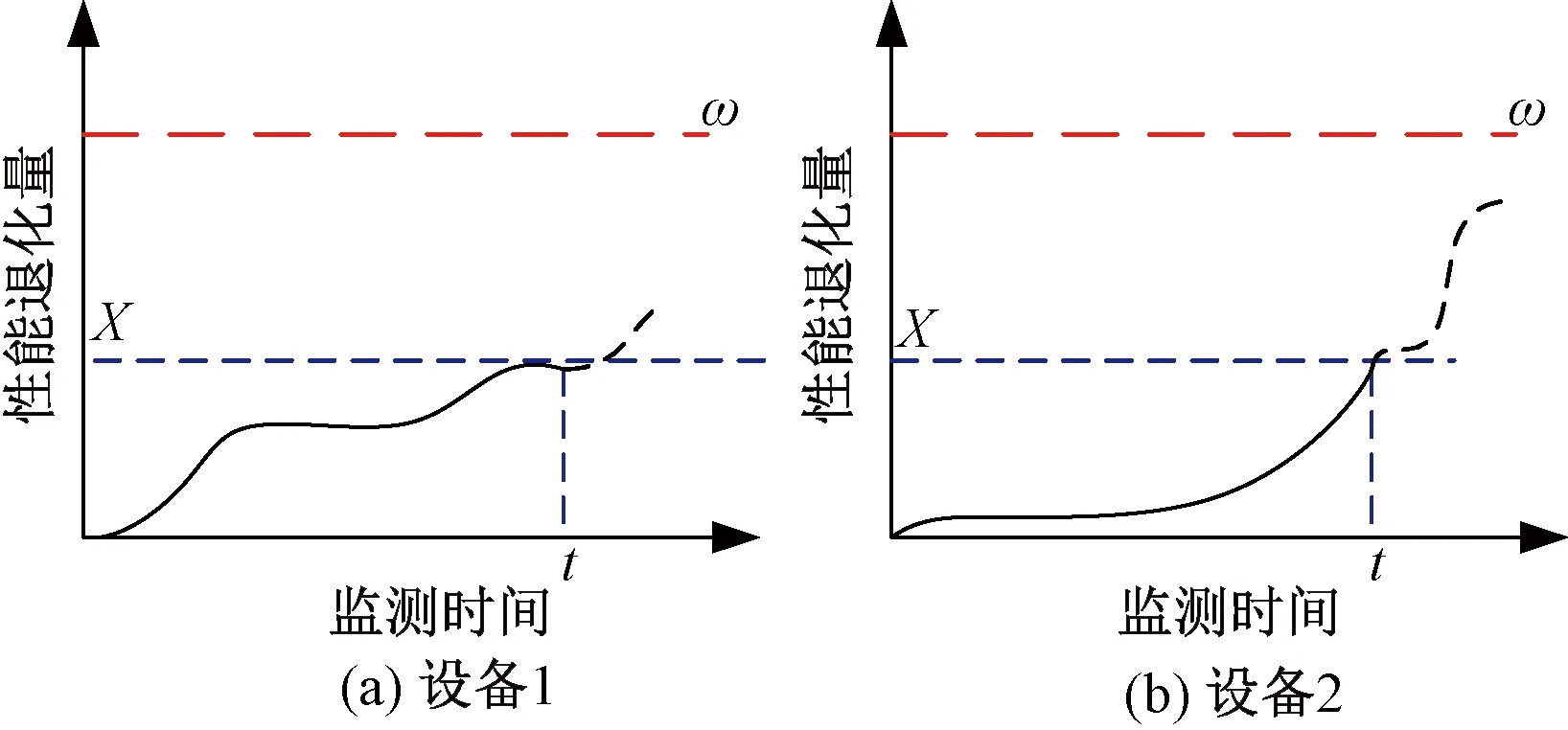
图3 性能退化轨迹的个体差异性
为了充分利用设备性能退化轨迹信息,假设当前监测时刻为tk,单部件的性能退化模型可以重构为以下状态空间模型
( 2 )

依据式(2)和STF滤波技术的高斯特性可知,基于X0:k的漂移状态λx的概率密度分布为高斯分布,即
( 3 )
2.1.2 单性能参量的RUL分布
基于性能退化过程首达时间的概念,认为当性能退化过程{X(t),t≥0}初次到达预先设定的性能指标失效阈值ω时,判定部件发生了失效。因此,性能退化模型{X(t),t≥0}对应寿命的数学定义为
T=inf{t:X(t)≥ω|X(0)<ω}
( 4 )
根据式(4),文献[16]给出退化过程基于首达时间的寿命概率密度函数如下
( 5 )
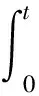
Lk=inf{lk:X(lk+tk)≥ω|X0:k}
( 6 )
由文献[2]的相关推论可知,基于性能退化过程的状态空间模型式( 2 )和部件运行到当前时刻的全部监测数据X0:k,监测时刻tk处RUL的概率密度分布fLk|X0:k(lk|X0:k)为
( 7 )
综上所述,每当监测获取新的性能退化数据xk,可通过漂移状态λk的更新机制,依赖全部历史监测数据X0:k,并利用式(7)自适应的更新RUL的概率密度分布,实现RUL的实时预测。
2.2 二元性能参量的相关性分析方法
2.2.1 二元Copula函数原理
Copula函数是把多个随机向量X1,X2,…,XN的联合分布函数F(x1,x2,…,xN)与各自对应的边缘分布函数u1,u2,…,uN相连接的函数,表达式为
F(x1,x2,…,xN)=C(u1,u2,…,uN;θ)
( 8 )
式中:C(u1,u2,…,uN;θ)为Copula函数。其中,θ为相关性参数;ui为第i(i=1,2,…,N)个随机变量的边缘分布。
Sklar定理是用来证明Copula函数存在性的定理。其中,针对二元变量联合分布的Sklar定理为:
假设H(x,y)是边缘分布分别为F(x)、G(y)的二元变量联合分布函数,则必定存在一个Copula函数C(u1,u2)满足H(x,y)=C[F(x),G(y)]。若F(x),G(y)是连续函数,那么C(u1,u2)唯一确定;相反,若F(x)、G(y)是一元分布函数,C(u1,u2)是Copula函数,则H(x,y)是具有边缘分布为F(x)、G(y)的二元联合分布函数。
2.2.2 二元Copula函数选择方法
根据Sklar定理,在已知Copula函数具体表达形式的前提下,可以更加灵活地建立多元变量间的联合分布。
选择对多元变量间相关性描述适配度较高的Copula函数,有助于提高基于二元性能退化过程RUL预测的精度。本文基于性能指标的边缘分布和Coupla相关基础理论,通过边缘分布的二元直方分布特性及其与经验Copula函数的欧氏距离,综合评判选取最佳适配Copula函数来描述两个性能变量间的动态相关性。
定义经验Copula:设(xi,yi)(i=1,2,…,n)为取自二维总体(X,Y)的样本。将X,Y的经验分布函数分别记为Fn(x)和Gn(y),得到样本的经验Copula函数定义如下
(9)
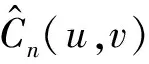
2.3 二元性能参量的剩余寿命建模
2.3.1 二元性能参量退化过程
假设基于二元性能指标设备的性能退化过程Z(t)={X1(t),X2(t),t≥0},其中,Xi(t)(i=1,2)为2.1.1节中描述的单部件性能退化过程,并且满足以下假设:
假设1:设备两个性能指标的退化过程均可利用带线性或非线性漂移的Wiener过程进行建模,如式(1)。
假设2:针对同一设备,两个性能指标的监测时间和间隔保持同步。
假设3:两个性能指标的退化存在相关性,且相关性可以利用某种二元Copula函数进行合理描述。
假设4:当设备的任意一个性能退化过程的退化量超过其对应失效阈值时,视作设备失效,设备的失效阈值向量记为W=[ωi],i=1,2。
2.3.2 RUL联合分布模型
假设设备在当前监测时刻tk未发生失效,根据式(6)和二元性能退化过程失效定义(假设4),基于二元性能指标设备的RUL定义如下
(10)
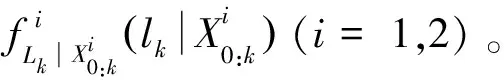
(11)
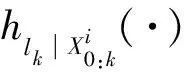
(12)
3 预测模型参数分步自适应更新方法
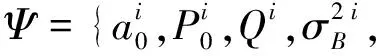
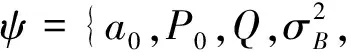
3.1 性能退化模型参数自适应估计算法
假设单性能指标退化模型中“隐含”状态λ的历史数据为Υk={λ0,λ1,…,λk},EM算法的基本原理是通过最大化联合似然函数p(X0:k,Υk|ψ)来逼近参数的极大似然估计。
图4为EM算法过程,L(θ)为完全数据的极大似然函数,B(θ,θi)为极大似然函数的下界函数,当且仅当θ=θi时,两函数值才相等。在E步,已有一个估计的参数值(初始化或上次迭代计算出的参数),但是此时这个参数值对应B(θ,θi)的值不等于L(θ)的值。因此在E步以当前的估计参数,极大化B(θ,θi),使得该参数对应的B(θ,θi)与L(θ)的数值相等。结果见图4,θ=θi处极大似然函数与下界函数的函数值相等。在M步,求出使得B(θ,θi)取得极大的参数θi+1,然后将其作为下一次迭代的当前参数值。
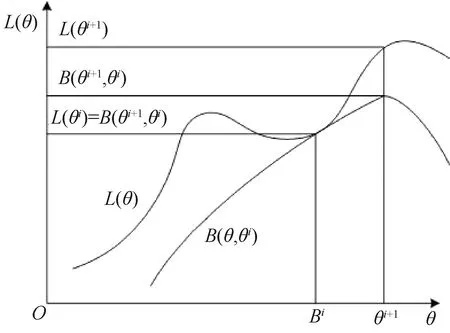
图4 EM算法过程图
EM算法主要步骤包括:
E步-对似然函数求期望得
(13)
M步-求极值
(14)
最后,通过EM算法循环迭代可得到ψ的最终估计值。
其中,根据单性能指标退化过程的状态空间模型式(2),E步-计算期望可以表示为
(15)
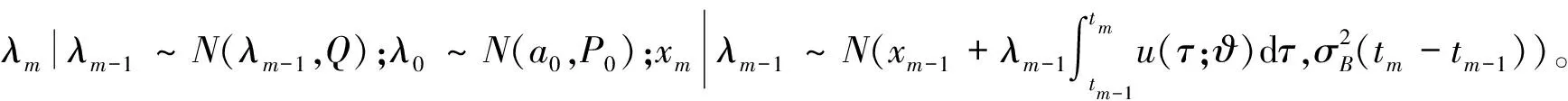
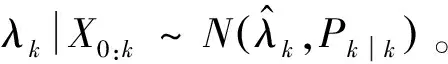
Step2后向迭代最优平滑估计。
form=k:1
Step3协方差初始化。
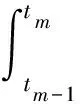
Step4平滑协方差的后向迭代计算。
Zm|k=Pm|mJm-1+Jm(Zm+1|k-Pm|m)Jm-1
(16)
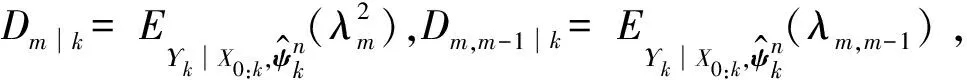
(17)
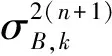
(18)
3.2 Copula函数未知参数估计
(19)
于是得到对数似然函数为
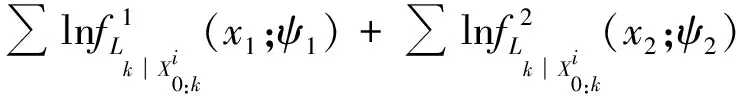
(20)
求解对数似然函数的最大值点,即可得Copula函数的未知参数的估计为
(21)
未知参数向量Ψ自适应的更新估计流程如下。
Step1将模型参数Ψ分成两部分:ψ退化模型参数和Copula函数的参数θ。
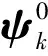
Step3基于EM算法性能退化模型参数的自适应预测:
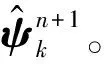
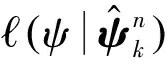
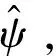
4 仿真测试与验证
本节针对第2、3节提出的列车定位惯性单元的RUL自适应预测方法,利用第1节中描述的惯性单元性能退化的实际监测数据,进行实验分析和模型、算法的有效性验证。
4.1 惯性单元性能监测数据分析
根据铁路应用RAMS标准,列车定位惯性单元中惯性器件的失效阈值如表1所示,陀螺仪的性能退化轨迹于第64个监测点达到失效阈值,加速度计的性能退化轨迹于第85个监测点首次到达失效阈值。由设备失效定义推知,该实验设备在初始监测点的真实RUL为64周。
4.2 基于单性能指标的剩余寿命预测
陀螺仪和加速度计在每个监测点处的实际退化量与一步预测结果的均方误差(MSE)见图5。预测的退化轨迹在前期由于数据不够充足与实际退化轨迹略有出入。此外,陀螺仪和加速度计性能退化量预测MSE的期望分别为0.71×10-2与0.64×10-4。特别的在设备判定的失效监测点处,陀螺仪性能退化量预测的MSE为0.21×10-2,加速度计性能退化量预测的MSE为0.47×10-4。表明本文采用的非线性漂移Wiener过程可以对不同类型的惯性器件的退化过程进行有效建模。
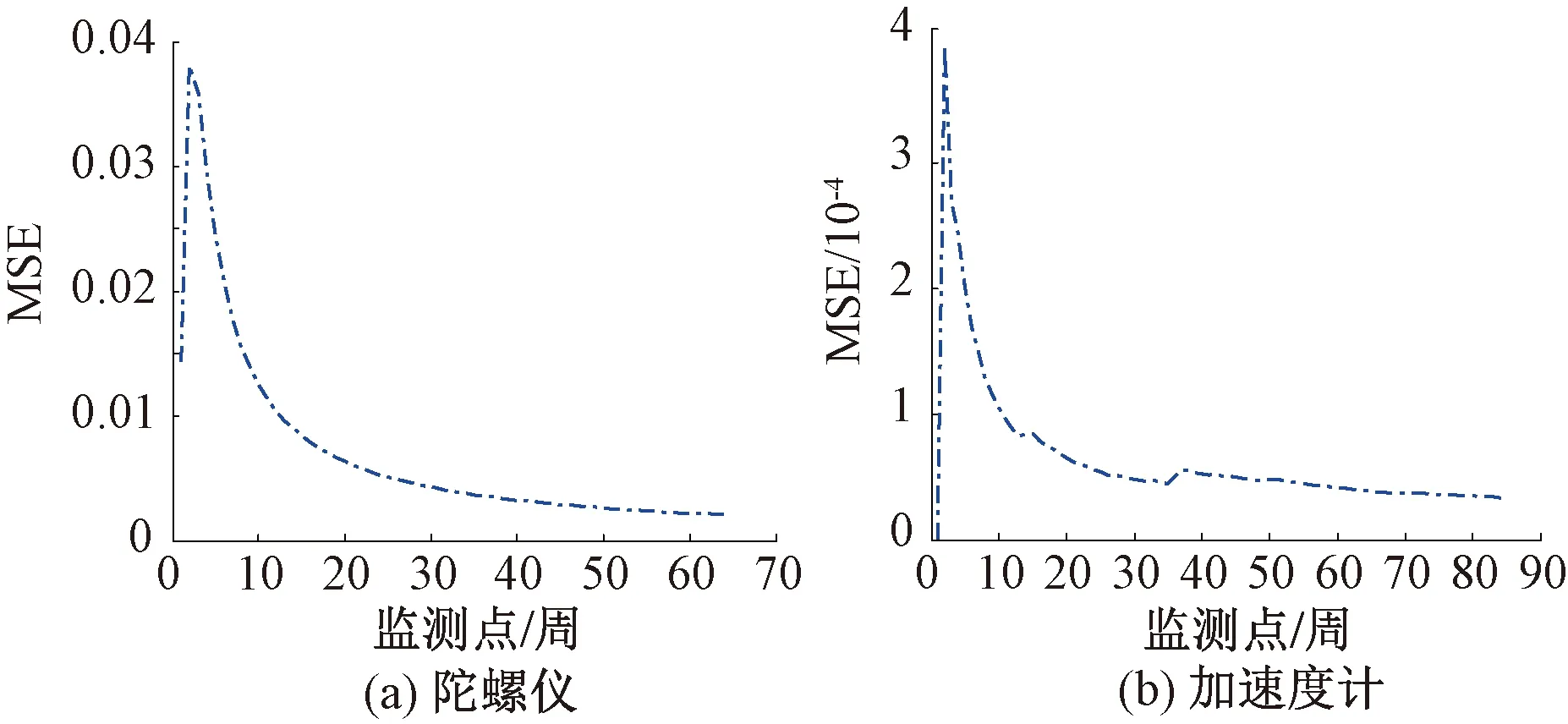
图5 惯性器件性能退化量一步预测的MSE
由式(17)和式(18)计算可以得到陀螺仪、加速度计性能退化模型参数随着性能监测数据的累积,在各监测点自适应估计、更新的轨迹见图6、图7。由图6、图7可见,模型参数可以敏感性能退化过程的状态变化保持更新。与参考文献[10]中使用EM算法对共轭先验分布函数超参数值进行估计方法相比,本文提出的参数分步自适应估计的方法不受先验初始化信息的影响,具有良好的鲁棒性,为实现RUL的自适应预测奠定基础。
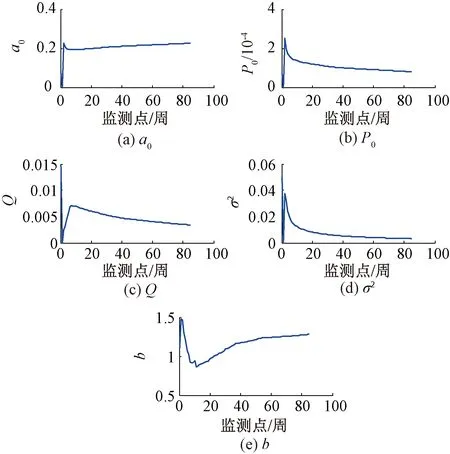
图6 陀螺仪性能退化模型参数更新曲线
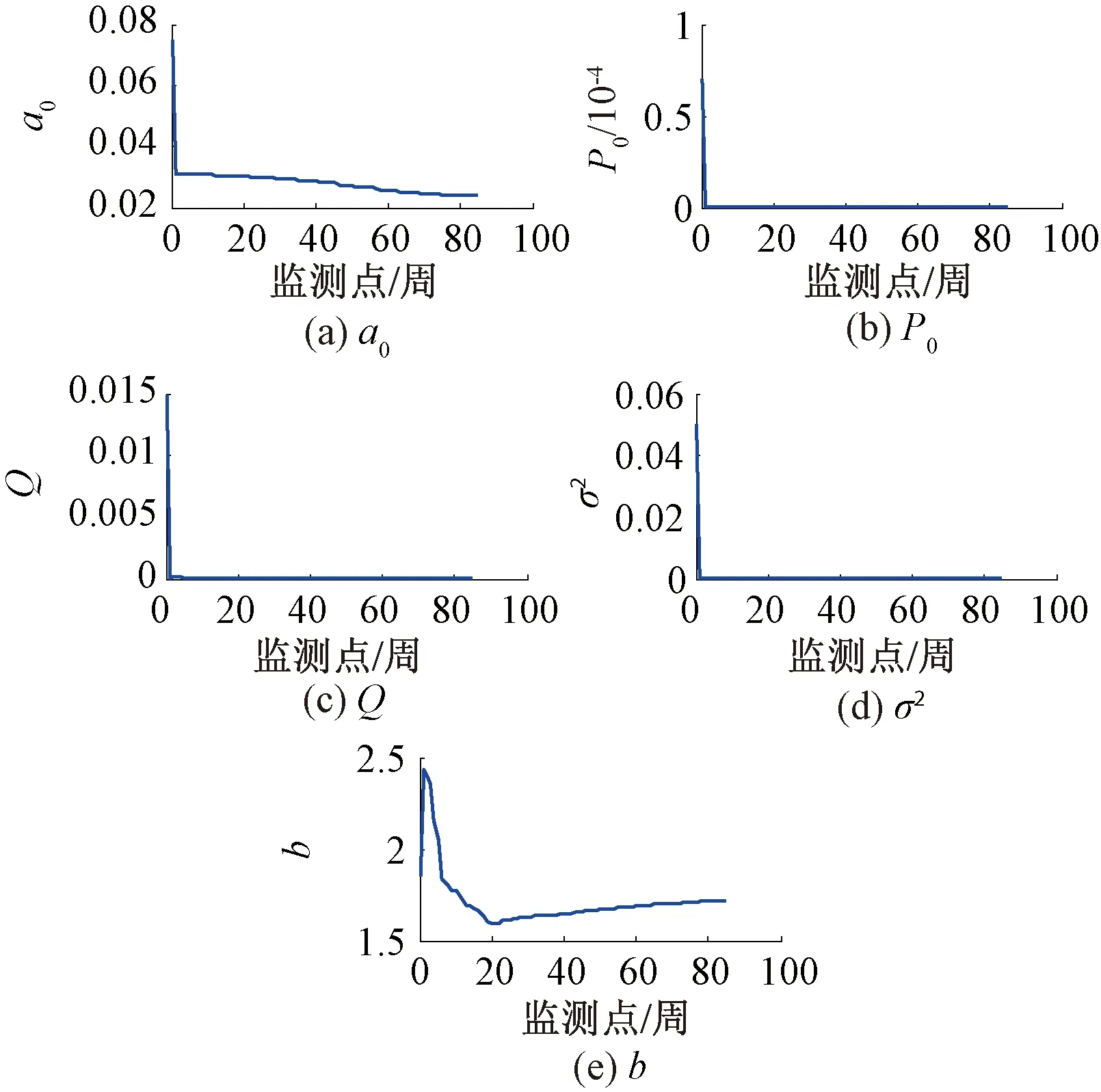
图7 加速度计性能退化模型参数更新曲线
已知各惯性器件的失效点,由此可推出在每个监测点处惯性器件的实际RUL。为进一步定量评价RUL预测结果,定义实际RUL与RUL预测的期望均方误差(EMSE)为
(22)
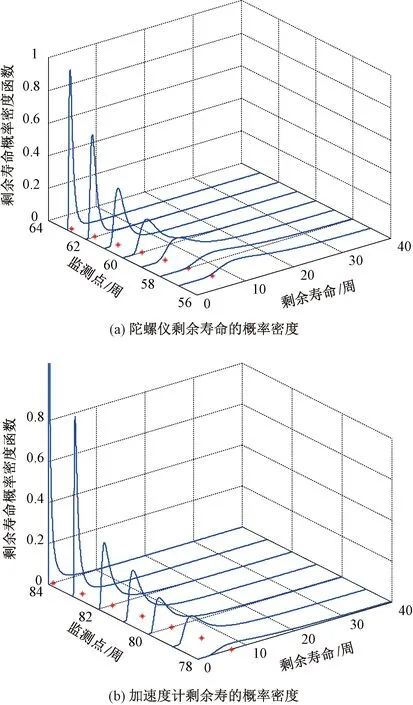
图8 单性能指标RUL自适应预测结果
图8(a)、图8(b)为惯性器件失效前多个关键监测点处剩余寿命的PDF曲线,可看出预测的PDF曲线包含实际剩余寿命点,并随着监测数据的累积曲线逐渐变窄,意味着RUL预测的不确定逐渐减小。
图9(a)、图9(b)为惯性器件在各个监测点剩余寿命预测的EMSE,在惯性器件各自的失效点处,陀螺仪RUL预测的EMSE为0.72,加速度计的EMSE为0.33。通过观察EMSE曲线可以得出随着数据累计RUL的预测精度将不断提高。
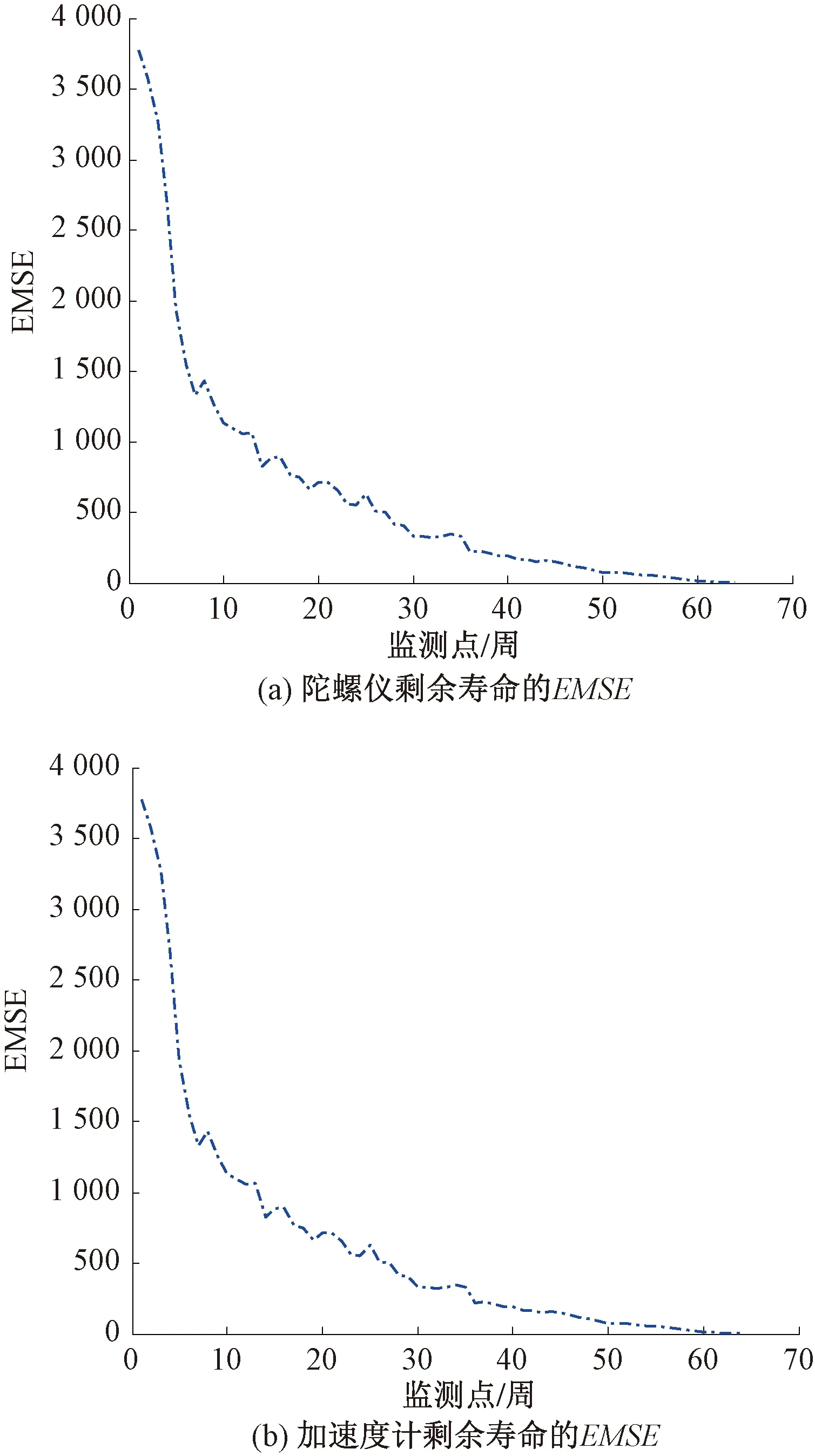
图9 单性能指标RUL的EMSE
4.3 基于Copula函数的剩余寿命预测
通过将设备失效前多个关键监测点处的二元分布直方图,与不同形式Copula函数的分布密度图进行对比,可以初步选定的Copula函数类型有Gaussian、Frank和Gumbel函数。接着,根据极大似然估计的方法对相应Copula函数的未知参数进行估计,并据此求解欧氏距离,依据距离越小相关性描述越精准的原则,选定Gumbel函数作为描述二元变量相关性的Copula函数。
完成Copula函数选择和基于式(21)的参数极大似然估计后,根据式(12)计算设备的实时剩余寿命概率密度函数,得到设备RUL概率密度曲线见图10。
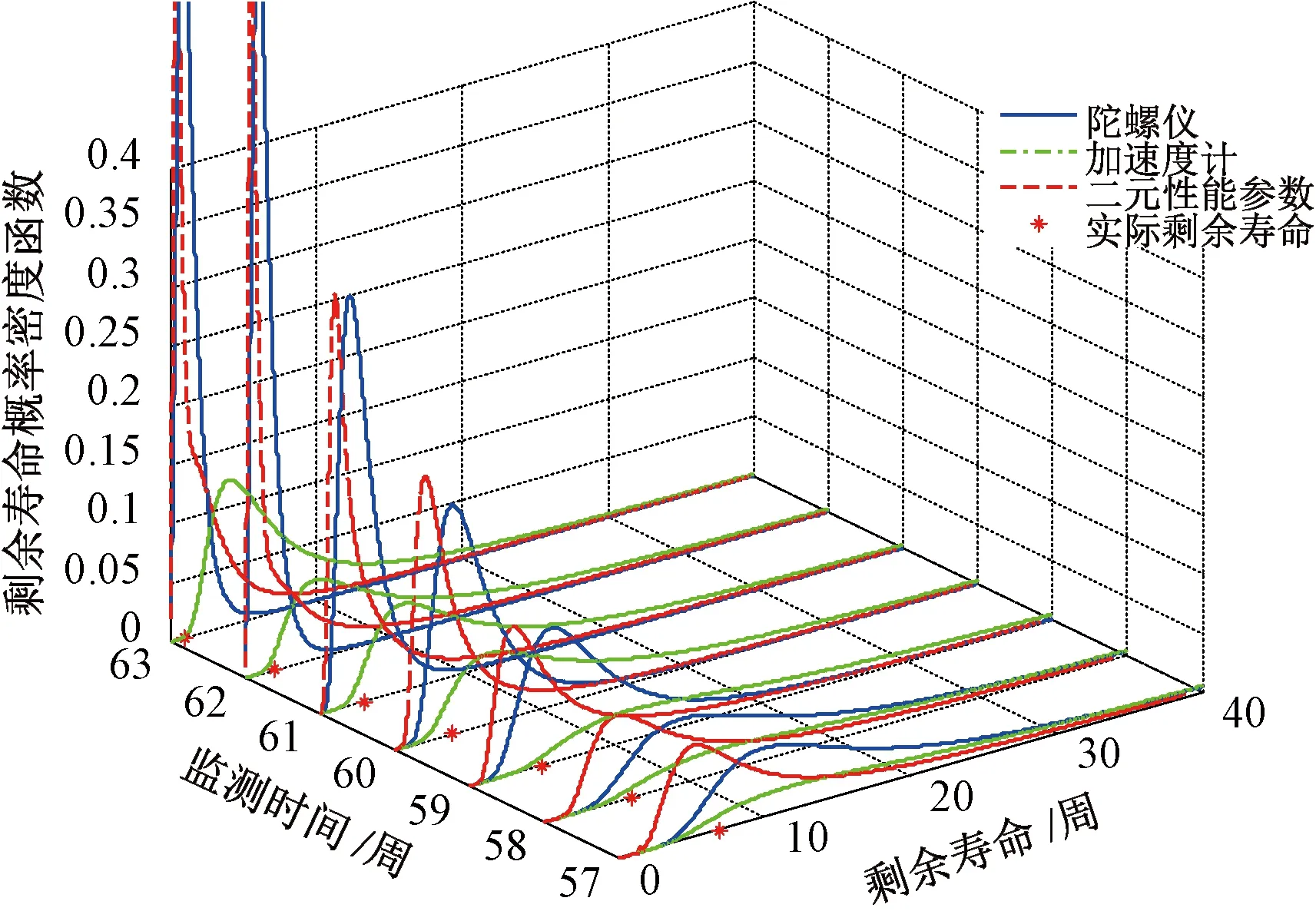
图10 RUL概率密度曲线
蓝色实线是陀螺仪的PDF预测曲线,绿色点划线是加速度计的PDF预测曲线,红色虚线为基于陀螺仪和加速度计二元性能参量的PDF预测曲线。相较于另外两条PDF曲线,二元性能参量的预测曲线方差较小、收敛更加集中、尖锐,具有较高的峰值。
在失效前的最后6个监测时刻,分别采用陀螺仪性能指标、加速度计性能指标和二元性能参量3种不同性能退化指标,计算RUL预测期望值,并计算预测的RUL期望值与实际RUL的均方相对误差(MRE)为
(23)
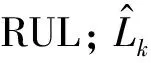
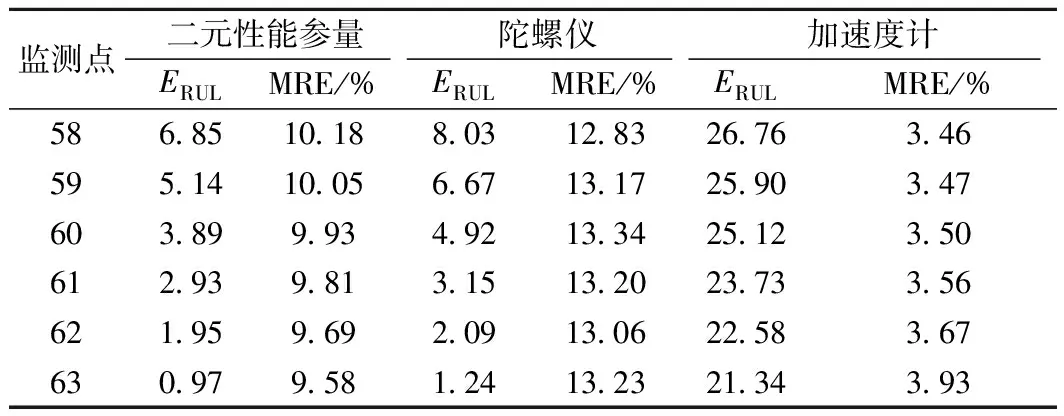
表5 基于3种性能指标方案的RUL预测的期望和MRE
由表5可知,在失效前最后6个监测时刻,考虑二者相关性RUL预测期望值的平均MRE为9.87%,基于陀螺仪RUL预测的平均MRE为13.14%。可明显看出本文提出的基于Copula函数的二元性能参量剩余寿命预测方法可以充分利用设备组成部件的性能退化信息,提高RUL预测精度。
5 结论与展望
本文主要针对列车定位惯性单元RUL预测方法进行研究,基于列车定位惯性单元的性能评价指标体系,构建了基于Copula函数的二元性能参量剩余寿命联合分布模型,并采用未知参数自适应分步更新的方法,实现RUL的自适应更新预测。结果表明,本文提出的基于二元性能参量的RUL预测方法可以提高预测精度,对存在多个退化变量且它们关系未知的设备的剩余寿命预测有着重要的参考价值。
后续工作中在列车定位惯性单元具有较多退化、失效数据时,可以结合机器学习与随机过程方法预测设备RUL,进一步丰富RUL预测结果,提高RUL的预测性能。

