高速道岔尖轨弹性波频散特性研究
陈 嵘,龚 政,胡辰阳,徐井芒,刘 乐,王 平
(1.西南交通大学 高速铁路线路工程教育部重点实验室,四川 成都 610031;2.西南交通大学 土木工程学院,四川 成都 610031)
道岔作为高速铁路线路的薄弱环节及养护维修的重点和难点,其构造复杂、状态多变、病害繁多,是影响行车平稳性与安全性的关键基础设施[1]。道岔尖轨是道岔结构的重要组成部件,尖端由60D40钢轨铣削加工而成,跟端压型为区间线路所采用的CHN60钢轨断面形状,其弹性波传播特性的研究,对道岔钢轨伤损病害的无损检测[2]以及揭示弹性波作用下裂纹的动态扩展机制[3]具有指导性作用。基于此,迫切需要开展高速铁路道岔尖轨弹性波传播特性的基础理论研究,以保证高速铁路的安全运营。
钢轨截面几何形状复杂,在较高频率下很难使用解析方法建立弹性波波动方程,对其频散特性进行求解分析。为此,众多学者结合有限元法,发展了适合复杂波导结构频散特性求解的数值方法[4]。其中,半解析有限元法因其计算效率高、求解简便,已成为求解异形波导截面弹性波频散特性的最常用方法。Aalami[5]于1973年首次证明了半解析有限元法对任意波导截面的适用性,只需对结构横截面进行离散,用谐波指数函数描述沿波传播方向的位移,从总体运动方程解得特征值后,便可获得频散特性曲线;Hayashi等[6]将该方法应用于钢轨的频散特性求解,绘制了钢轨在100 kHz频率以内的相速度和群速度频散曲线,并通过试验验证了结果的正确性;王嵘等[7]基于该方法,推导并求解了存在初始应力钢轨的波动方程,得到了存在初始应力下钢轨频散曲线。此外,有学者利用波有限元法[8]、振动模态分析法[9]等对区间线路等截面钢轨弹性波传播特性进行研究。
区间线路等截面钢轨弹性波传播特性研究成果较多,道岔尖轨由于截面非对称以及沿线路纵向变化的特性,其弹性波传播特性相关研究相对较少。严寅中[10]基于传统有限元方法,建立了12号道岔尖轨瞬态分析模型,研究不同频率弹性波在尖轨中的时域传播规律,并与试验结果较好地吻合。范振中[11]将道岔尖轨不同部位近似成不同厚度的平板波导,基于解析方法推导并求解了不同部位关键厚度下的频散方程,研究了道岔尖轨各部位的兰姆波最优激发频率与激发角度。Zhang等[12]采用连续小波变换方法对尖轨内接收到的声发射波信号进行频域分析,研究了尖轨缺陷信号的兰姆波频散特性,以实现轨底缺陷的识别和定位。付连著等[13]采用半解析有限元法计算了道岔60AT钢轨的相速度、群速度频散曲线,结合仿真与试验确定了适用于60AT钢轨轨腰及轨底窄边检测的弹性波模态及频率。
可以看出,道岔尖轨弹性波传播特性研究刚刚起步,且大多数研究仅从时域的角度出发,通过试验或有限元仿真研究特定频率弹性波传播特性,尚不能系统地描述道岔变截面钢轨弹性波传播特性。基于此,本文通过建立考虑截面纵向变化的高速铁路道岔尖轨弹性波传播特性分析方法,提出包含截面位置信息的三维频散曲面,揭示弹性波在高速铁路道岔钢轨中的传播规律,进一步地可以结合三维频散曲面和波结构的能量分布特性,指导道岔变截面钢轨弹性波无损检测激励频率和激励模式的选取,研究弹性波作用下道岔钢轨裂纹的动态扩展机制。
1 钢轨频散特性
高速道岔尖轨由60D40钢轨加工而成,其前端经过铣削形成变截面区段与基本轨贴靠,进而引导车辆的行驶方向,跟端采用热锻成型工艺过渡为CHN60钢轨断面形状,并与道岔连接部分钢轨焊接成整体[14],图1为道岔尖轨加工示意图。
对道岔尖轨弹性波传播特性的研究,首先要分析弹性波在60D40和CHN60两种形状断面钢轨内的频散特性。其中,CHN60钢轨广泛应用于区间线路,相关频散特性的研究较为成熟[15-17],而关于60D40钢轨频散特性的研究仍处于起步阶段,且两种钢轨频散特性不同。本节求解得到60D40钢轨和CHN60钢轨的频散曲线,对比两种钢轨在10 000 Hz内的波结构特征,分析其频散特性。
1.1 求解钢轨频散特性的半解析有限元法
对于截面非规则的钢轨,在较高频率下,无法建立解析解的波动方程研究弹性波的频散特性。使用半解析有限元法,首先对两种钢轨截面进行有限元离散,网格划分结果如图2所示,图中每个节点都具有空间上的三个自由度,弹性波在x方向上传播,横断面在yz平面。
沿弹性波传播方向x的位移用简谐波的振动方式表示,用空间分布函数描述任意一点在横截面平面yz的振幅,即
(1)
式中:t为时间;ξ为波数;ω为弹性波角频率。
结合哈密尔顿余能原理,推导可得等截面钢轨弹性波的波动方程[5]为
(2)
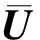
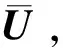
1.2 结合波结构的频散特性分析
基于半解析有限元法,通过对CHN60钢轨和60D40钢轨波动方程特征值以及特征向量的求解即可得到弹性波频散曲线和相应的波结构。图3为两种钢轨自由状态下0~10 000 Hz范围内波数频散曲线,此处求解得到的CHN60钢轨频散曲线与采用半解析有限元方法的文献[16]和基于钢轨周期子结构波导模型的文献[18]一致。
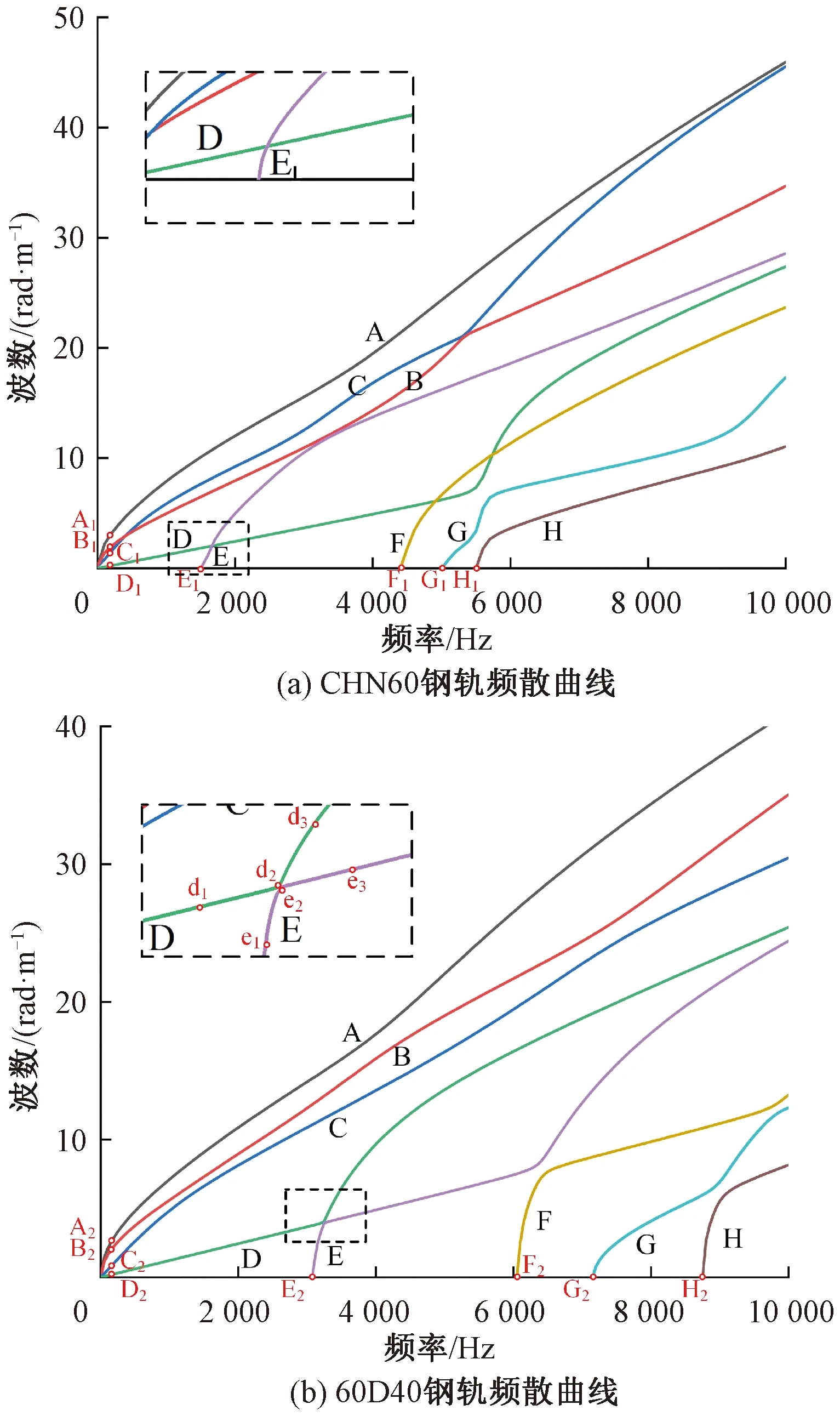
图3 钢轨频散曲线
如图3所示,每条频散曲线代表一种在钢轨中可传播的波模式,组成频散曲线的每个点都包含该波模式在特定频率和波数的振动特征信息。在10 000 Hz以下频率范围内,两种钢轨均存在8种波模式,图3中分别以字母A~H命名。对于任一固定的波模式,波数为零时对应的频率为其截止频率,意味着该模式弹性波可传播的最低频率,并随着频率的升高,其波数逐渐增大。
两种钢轨中均存在四种截止频率为0 Hz的基本波模式,分别对应频散曲线上的A、B、C和D。图4绘制了两种钢轨200 Hz下各频散曲线上圆圈标注的频率-波数点对应的波结构,并标注其波数。
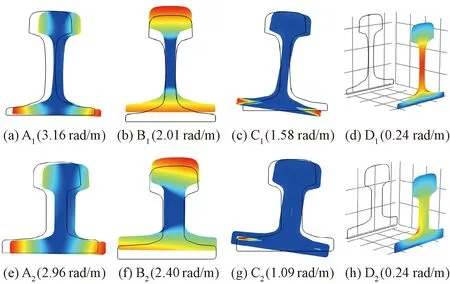
图4 两种钢轨200 Hz各波模式对应波结构
可以看出,这四种波模式在200 Hz时表现为横向弯曲、竖向弯曲、扭转以及纵向伸缩,对应波数依次减小。CHN60钢轨与60D40钢轨相比,横向弯曲波,扭转波的波数较大,竖向弯曲波的波数较小,而纵波的波数相同,这均能由铁木辛柯梁理论得到较好解释,频率较低时波数与相对应的变形刚度相关。
波模式类型随频率的增大而增多。在所研究的频率范围内,两种钢轨均存在四种截止频率不为0的波模式,经过对波模式对应的波结构进行分析,结合能量分布特点和变形模式发现,在截止频率附近CHN60钢轨的E、F、G、H波模式分别与60D40钢轨中的E、H、G、F波模式类似,这是由于两种钢轨构造的相似性,导致其波模式在截止频率下的相似性。图5绘制了两种钢轨相似波模式下波数为0的波结构,并标注其截止频率。可以看出,虽然波结构相似,但是其截止频率有较大差异。相似波结构下,CHN60钢轨截止频率均小于60D40钢轨。这是由于CHN60钢轨各部分较60D40钢轨更为长细,相应的变形刚度更低,较低频率下可出现该种波模式。
由图4和图5中可知,虽然两种钢轨D和E波模式对应的波结构类似,但在图3中,CHN60钢轨D和E两种波模式对应的频散曲线相互交叉穿过,而60D40钢轨D和E两种波模式对应的频散曲线表现为相斥偏转。为进一步说明这种现象,在60D40钢轨D和E两种波模式对应的频散曲线偏转区选取6个频率-波数点,并绘制其波结构,如图6所示。
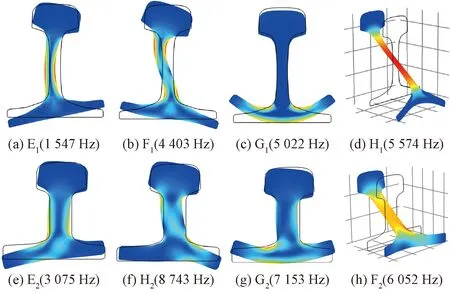
图5 两中钢轨相似波模式截止频率对应波结构
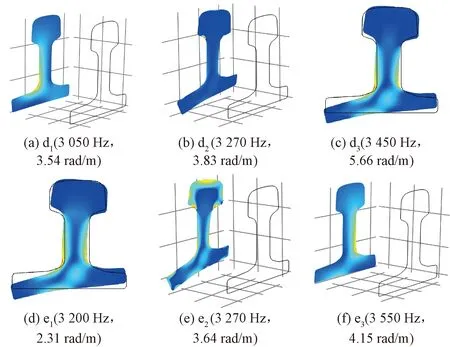
图6 偏转区各波数点对应波结构
可以看出,在曲线偏转区域的波结构具有D、E两种波模式的波结构特性,既有d1和e3波结构中沿纵向的位移,又有e1和d3波结构中轨头轨底相对轨腰的转动。在偏转区域后,两种波模式的波结构发生互换。这是由于在截面对称的钢轨中,正对称和反对称的波模式相互独立、互不影响,故对应的频散曲线交叉穿过。例如,CHN60钢轨频散曲线中正对称的D波模式与反对称的E和F波模式对应的频散曲线均相互交叉穿过,而正对称的G和H波模式的频散曲线相斥偏转。由于截面非对称的60D40钢轨中波模式不存在对称性,所以频散曲线均以曲线偏转的形式出现。
2 考虑变截面因素的频散特性分析方法
2.1 方法概述
为研究弹性波在高速铁路道岔变截面钢轨中的传播特性,首先要建立合理的道岔变截面钢轨弹性波传播特性数值分析方法。
波导结构频散特性与截面形式有直接关系。考虑高速道岔变截面钢轨实际截面沿纵向连续缓慢变化的特征,在局部表现出与等截面钢轨相似的弹性波传播特性,经过对不同位置各断面频散曲线求解,发现相近断面之间的频散曲线基本一致,对于截面连续变化的变截面钢轨,其频散特性沿波导纵向连续缓慢变化。基于此,本文提出包含截面位置信息的三维频散曲面来描述高速道岔钢轨变截面钢轨弹性波传播特性。首先将变截面道岔钢轨沿纵向划分成n段,横断面间距应保证能够反映钢轨断面的纵向连续变化特征,分别计算变截面钢轨n+1个断面的频散曲线,然后将不同断面类似波模式的频散曲线按照纵向位置拟合生成“波数-频率-位置”三维频散曲面,如图7所示。
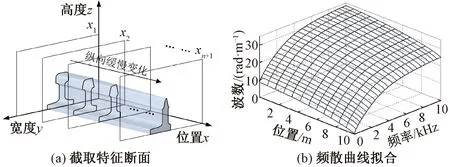
图7 频散曲面建立过程示意
频散曲面可以反映出不同位置断面的频散曲线以及相似波模式频散特性沿纵向的变化规律,结合频散曲面上的“波数-频率-位置”点对应的波结构,进一步对弹性波在变截面钢轨中传播规律进行研究。
2.2 道岔尖轨频散曲面
本文针对18号高速道岔直尖轨,其变截面区段全长11 792 mm,顶宽由0过渡为72.2 mm,以顶宽1 mm为步长截取特征断面,未考虑磨耗和螺栓孔等影响截面完整性的因素。由于尖轨并无扣件系统的约束,且自由放置在滑床台板上,因此,钢轨考虑为无约束状态,基于半解析有限方法,求解各特征断面的频散曲线。
此处选取道岔尖轨铣削加工过程中四个关键控制断面的频散曲线进行对比分析,其分别位于道岔直尖轨的尖端、中间位置及铣削跟端,顶宽分别为0、35、40、72.2 mm,断面形式及其频散曲线如图8所示。
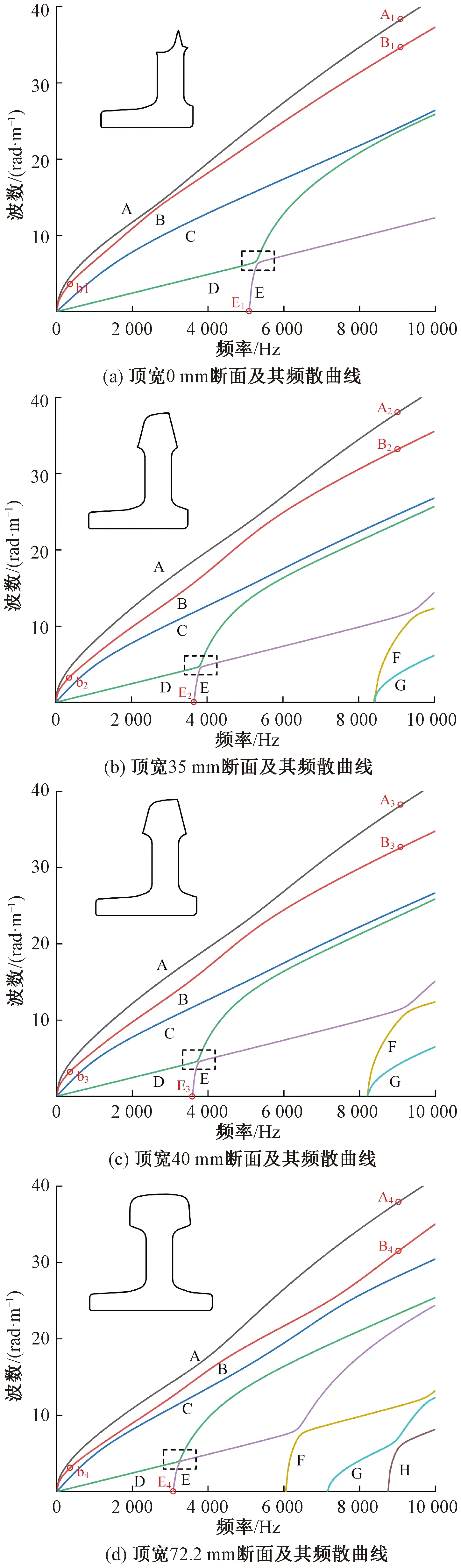
图8 不同顶宽断面频散曲线
在10 000 Hz以下频率范围内,四个断面中均存在四种截止频率为0的波模式,分别对应频散曲线上的A、B、C和D。对于截止频率不为0的各断面相似波模式,其截止频率大小从顶宽0断面至顶宽72.2 mm断面逐渐减小,波模式逐渐增多。由于截面沿纵向连续缓慢变化,频散曲线可以考虑为连续变化,顶宽35 mm断面与顶宽40 mm断面由于截面特性相近,各波模式对应的频散曲线基本一致。
此外,可以看出,四个断面中D波模式和E波模式对应的频散曲线均以曲线偏转的形式出现,这与前文结论是一致的。从顶宽72.2 mm断面至顶宽0断面,随着截面非对称特性的增强,这种曲线偏转的现象更加明显,进一步说明波导截面非对称特性与曲线偏转现象有直接联系。
基于频散特性沿纵向连续缓慢变化的特性,根据各断面频散曲线及其纵向位置分别绘制截止频率为0的A波模式与截止频率不为0的E波模式在10 000 Hz以下频率范围内三维波数频散曲面,如图9所示。
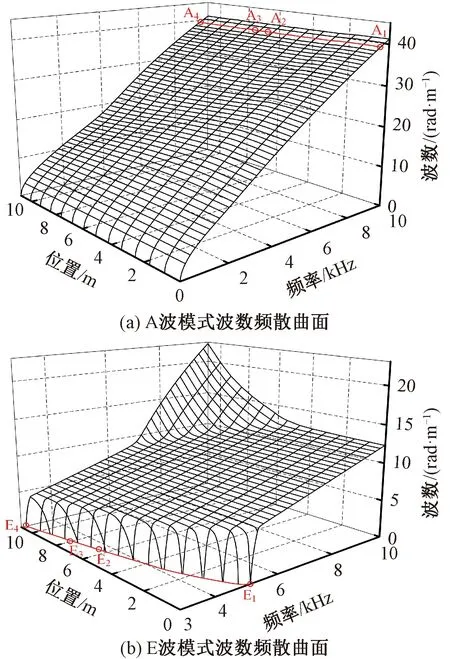
图9 波数频散曲面
对于不同位置断面的A波模式,频散曲线相近,频散特性沿纵向连续缓慢变化,当频率较高时,相同频率下的波数沿纵向基本一致,类似于等截面构件中的传播特性,说明该模式波在沿纵向传播时具有良好的一致性,受截面变化因素的影响较小。在E波模式频散曲面中,不同位置断面的截止频率不同,该模式波在由后端向前传播时,某些频率成分无法通过,发生反射或模式转换,形成一种高通滤波的作用。
2.3 变截面尖轨波结构特性研究
为进一步研究频散特性沿变截面尖轨纵向连续变化的特性,在不同顶宽断面频散曲线上以圆圈标注选取若干频率-波数点,并在频散曲面相应位置进行标注,如图8和9所示,各断面相近频散曲线用同一英文字母表示,以数字代表不同顶宽断面,绘制各波数-频率点相应波结构,通过不同断面波结构以及对应的波数或截止频率的变化规律进一步说明频散特性连续变化的特性。
在频率较低时,各断面均存在四种基本波模式:横向弯曲、竖向弯曲、扭转以及纵向伸缩,分别对应频散曲线的A、B、C和D波模式。图10所示为各断面B波模式200 Hz下波结构,表现为沿中性轴竖向弯曲,其波数与竖向弯曲刚度相关,随着顶宽与竖向抗弯刚度的增大波数逐渐减小。
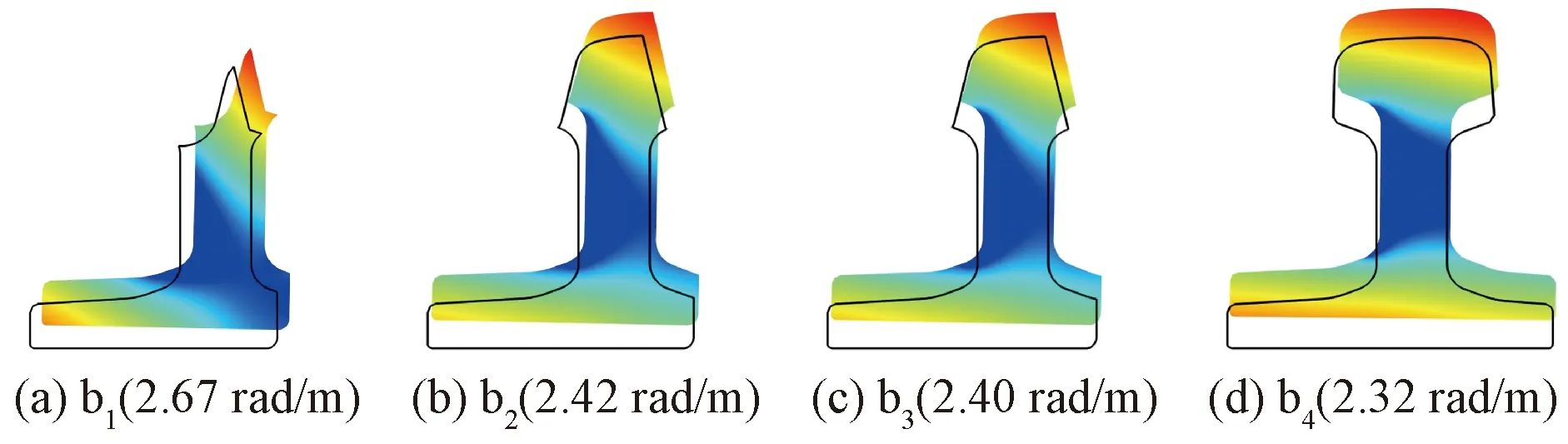
图10 各断面B波模式200 Hz波结构
当频率较高时,截面模态由整体的弯曲转化为局部的振动,图11和12分别为各断面A和B波模式9 000 Hz下波结构,其波数大小与局部振动区域的截面特性相关。对于A波模式,振动由全截面的竖向弯曲转换为集中在工作边方向轨底处,由于未经剖切,在不同位置钢轨截面特性保持一致,故在相同频率下各断面波结构与波数基本一致。可以发现,该波模式在较高频率下对应的波结构沿纵向具有良好的一致性,可以考虑作为道岔尖轨断轨监测或轨底裂纹检测的优选波模式。
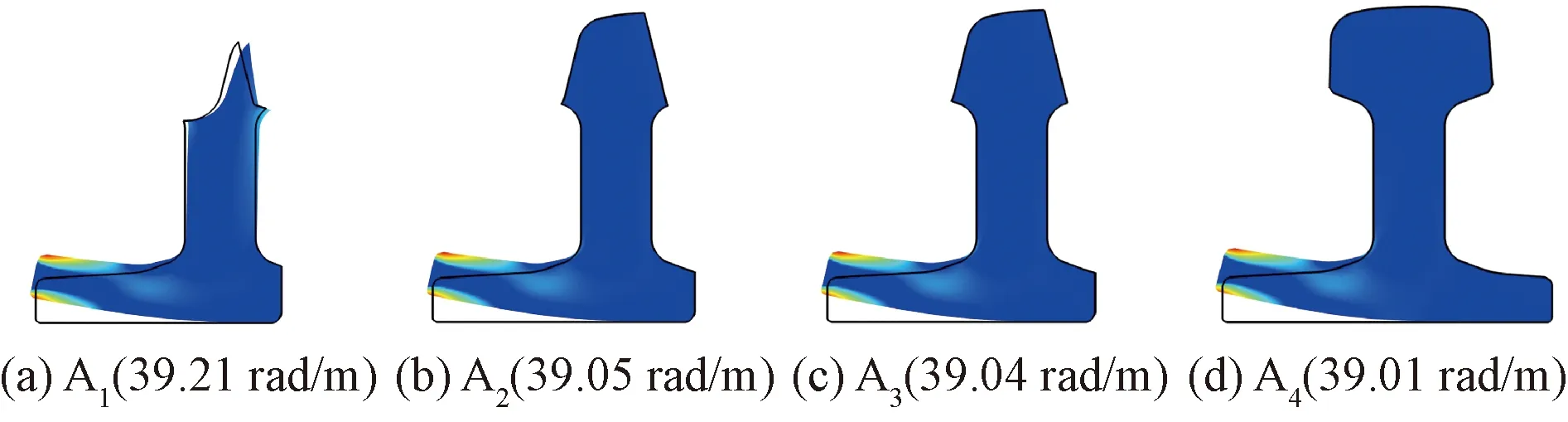
图11 各断面A波模式9 000 Hz波结构
对于横向弯曲模式,振动由全截面横向弯曲转换为集中在轨头处,由于轨头处经过铣削,在相同频率下,顶宽越大,其波数越低。
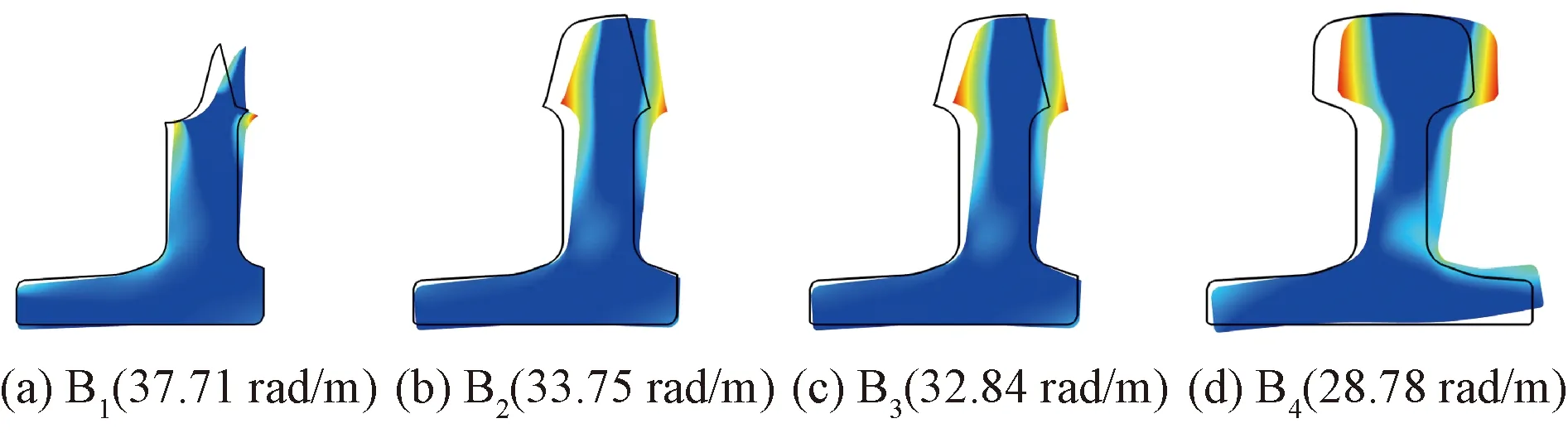
图12 各断面B波模式9 000 Hz波结构
对于截止频率不为0的各断面E波模式,其能量主要集中在轨腰与工作边方向轨底处,表现为轨腰与工作边轨底的相对转动,其波结构如图13所示,顶宽越大时,轨腰与轨底相对转动的刚度越低,该波模式的截止频率逐渐减小。
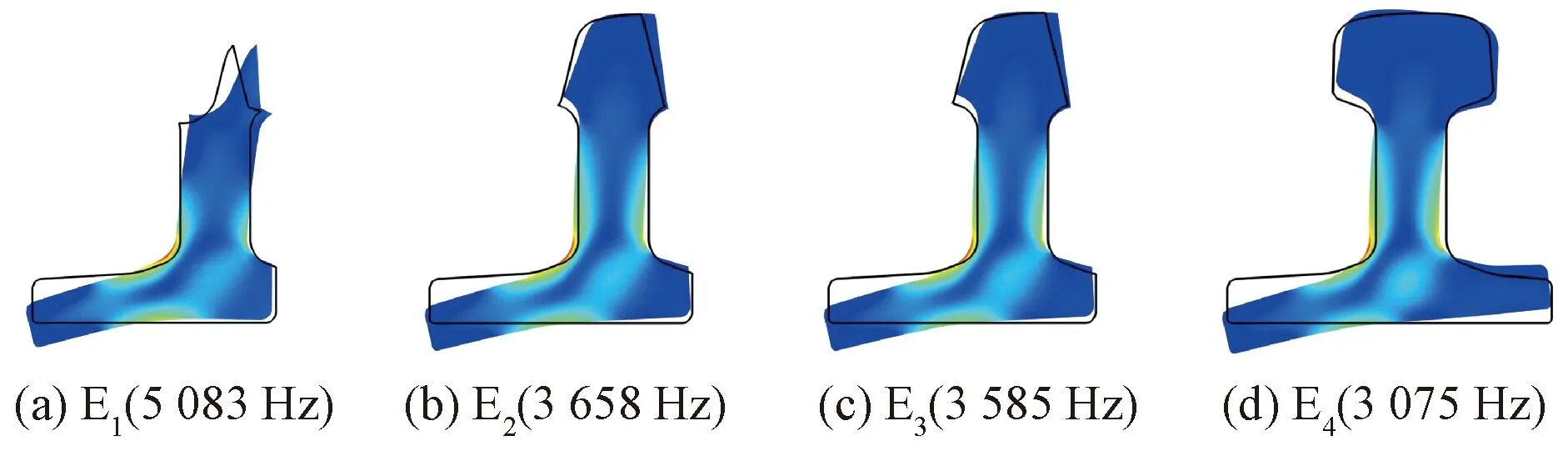
图13 各断面E波模式截止频率波结构
3 结论
本文针对高速道岔尖轨,基于半解析有限元法,求解得到尖轨跟端60D40钢轨和区间线路CHN60钢轨的频散曲线,对比两种钢轨在10 000Hz内的波结构特征,分析其频散特性。对于尖轨尖端由60D40钢轨铣削加工而成的变截面钢轨,首次提出了考虑截面位置信息的三维频散曲面对其弹性波传播特性进行研究,得到以下结论:
(1)CHN60钢轨和60D40钢轨存在相似的波模式,但是由于截面特性的差异,其相同频率下的波数或截止频率存在一定差别。
(2)60D40钢轨由于截面非对称特性,其频散曲线均会发生曲线偏转,并且非对称特性越强时,这种现象越明显。
(3)弹性波的频散特性以及相对应的波结构沿着道岔变截面钢轨的纵向连续缓慢变化。频率较高时,部分波模式的振动会集中于局部,其频散特性与局部截面特性相关。由于轨腰和工作边方向轨底未经剖切,存在某些特定的波模式,其频散特性沿纵向有良好的一致性,可以作为弹性波伤损检测的优选模式。
道岔钢轨结构复杂,现有研究多从时域角度出发,通过有限元仿真或试验研究特定频率或特定模式的弹性波传播特性,有一定的局限性。本文结合半解析有限方法,从频域角度出发,首次提出了频散曲面,对道岔变截面钢轨弹性波传播特性进行研究。下一步,将采用现场试验和有限元仿真,结合二维傅里叶变换,对变截面尖轨中时域导波信号进行处理,与求解得到的频散曲面进行对比验证,进一步研究该方法的有效性。

