变截面波形钢腹板组合箱梁剪力滞效应的比拟杆法求解

周 聪，汪建群，李立峰

(1.湖南科技大学 结构抗风与振动控制湖南省重点实验室，湖南 湘潭 411201；2.湖南科技大学 土木工程学院，湖南 湘潭 411201；3.湖南大学 土木工程学院，湖南 长沙 410082)

波形钢腹板组合箱梁具有自重轻、预应力导入效率高、完全避免腹板开裂等诸多优势，因此在我国得以迅速推广，目前已发展成为我国钢-混组合桥梁领域一种极具竞争力和发展前景的桥型[1]。同时，由于变截面梁相较于等截面梁具有跨越能力更强及应力分布更合理等特点，因而较后者在实际工程中应用更广泛。近年来，国内外学者针对该组合箱梁的力学性能开展了深入的研究，包括抗弯[2]、抗剪[3]、抗扭[4]以及波形钢腹板屈曲[5-6]等。

当薄壁箱梁承受竖向荷载时，由于上、下翼缘板发生面内剪切变形而导致翼缘板内纵向正应力沿横向不均匀分布，产生剪力滞现象。作为薄壁箱梁的一种基本力学特性，剪力滞效应在过去几十年间一直是研究热点。薄壁箱梁剪力滞效应的分析方法主要包括弹性理论解法、基于最小势能原理的能量变分法、比拟杆法和数值解法等。目前，针对传统薄壁箱梁剪力滞效应的研究已较为系统和完善。

剪力滞效应同样是波形钢腹板组合箱梁的基本力学特性之一。近年来，学者们提出了一些理论方法来分析该结构的剪力滞行为。文献[7-9]基于能量变分法对等截面波形钢腹板组合箱梁的剪力滞行为进行了理论分析。其中，吴文清[7]采用余弦函数来描述主梁的翘曲位移函数，李立峰等[8]、冀伟等[9]则选取了三次抛物线。向宇[10]、周茂定等[11]采用比拟杆法分析了等截面波形钢腹板组合箱梁的剪力滞效应，并进行了模型试验和数值模拟来验证分析方法的准确性。基于能量变分法并将钢腹板的剪切变形考虑在内，陈水生等[12]研究了等截面单箱多室波形钢腹板组合箱梁的剪力滞行为。文献[13-15]采用不同的广义位移函数来描述顶板、底板及悬臂板的翘曲位移函数，并基于能量变分法提出了用于评估等截面波形钢腹板组合箱梁剪力滞行为的理论方法。以上研究均针对等截面梁。迄今为止，针对变截面波形钢腹板组合箱梁剪力滞效应的研究较为有限。周勇超等[16]通过对比发现，采用二次抛物线来描述主梁的位移特征比采用其他曲线具有更高的计算精度。在此基础上，基于最小势能原理推导了变截面波形钢腹板组合箱梁剪力滞效应的控制微分方程，并采用差分法进行求解。

由上可知，在已有的波形钢腹板组合箱梁剪力滞效应理论分析方法中，多数基于能量变分法提出，并采用不同的曲线来描述主梁的翘曲位移函数。但是，目前位移函数的选取仍缺乏统一的准则，而位移函数又会显著影响理论方法的计算精度。此外，能量变分法的推导较为复杂，导致其难以在工程上广泛应用。相对而言，比拟杆法作为剪力滞效应的传统分析方法，具有易于推导、计算精度高和适于编程等诸多优势。该方法已被成功应用于波形钢腹板组合箱梁的剪力滞效应分析，并展现出了良好的适用性和精度[10-11]。但是，相关研究均只针对等截面梁，而由于变截面效应的影响，适用于等截面梁的理论方法不再适用于变截面梁的求解，需要重新进行推导。除此之外，在采用比拟杆法分析波形钢腹板组合箱梁剪力滞效应的相关文献中[10-11]，研究对象均为单箱单室截面，未讨论该方法在单箱多室截面中的适用性，因而具有局限性。

本文将通过理论推导，建立用于分析变截面波形钢腹板组合箱梁剪力滞效应的修正比拟杆法，并采用有限元方法验证所提出理论方法的有效性和准确性。探讨不同参数对变截面波形钢腹板组合箱梁剪力滞行为的影响规律。

1 修正比拟杆法-单箱单室截面

首先考虑具有单箱单室截面的变截面波形钢腹板组合箱梁，见图1(a)。在距梁左侧x处截取一横截面，该横截面尺寸见图1(b)。图1中，bo、bu分别为混凝土顶、底板的宽度；b1为钢腹板中心线至顶板最外侧的距离；b2为钢腹板中心线至桥轴中心线的距离；to、tu(x)、tw(x)分别为混凝土顶、底板和波形钢腹板的厚度；h1(x)、h2(x)分别为截面形心至混凝土顶、底板中心线的距离；h(x)为混凝土顶、底板中心线之间的距离；bo、bu、b1、b2、to沿主梁长度方向为常数；tu(x)、tw(x)、h1(x)、h2(x)、h(x)沿主梁长度方向为变量。将该变截面梁等效地离散为多根加劲杆与连接它们的薄板组成的加劲杆-薄板等效结构体系，见图1(c)。在推导过程中将混凝土顶、底板分别等效为9根和5根加劲杆，各杆的编号见图1(c)。

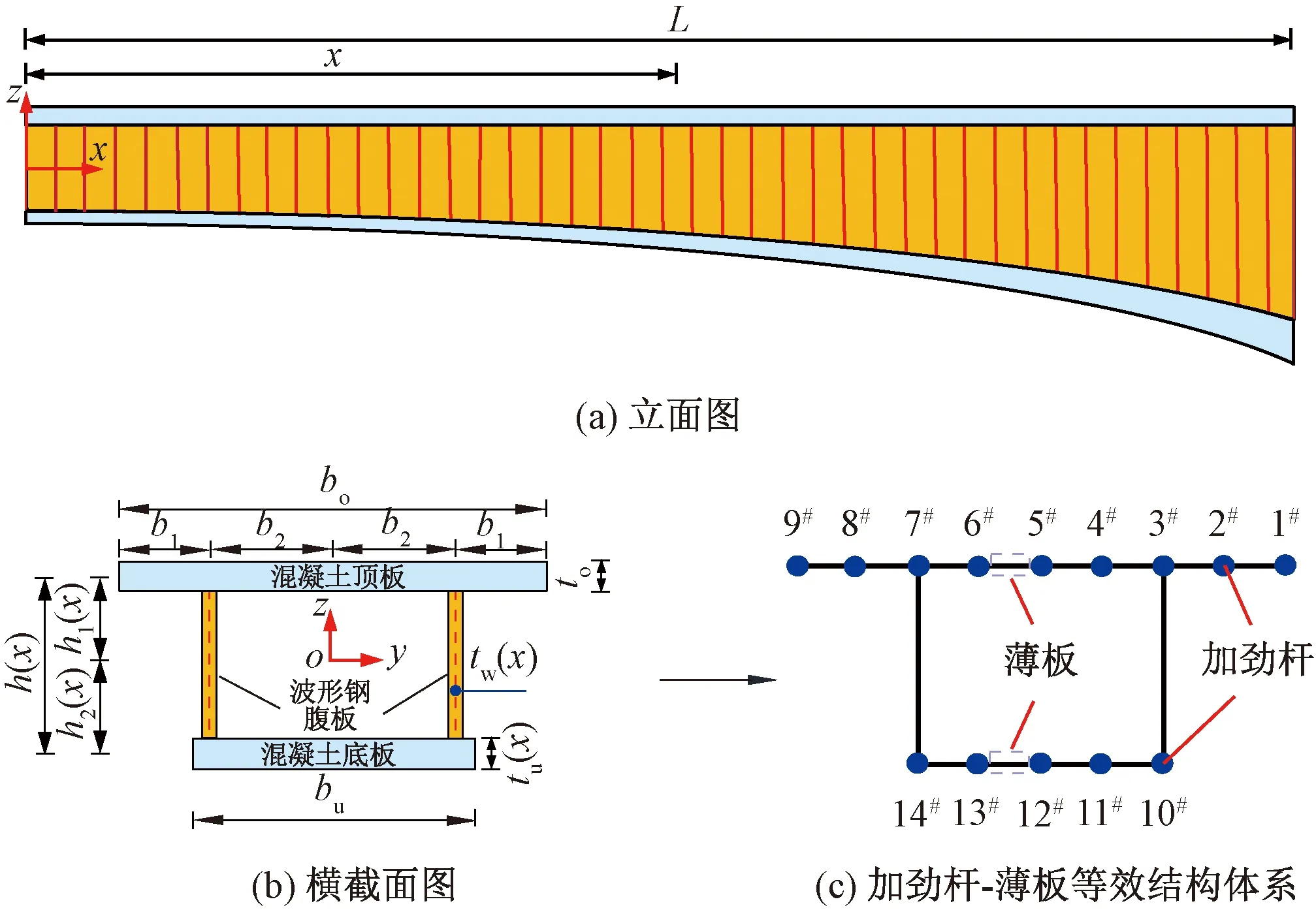
图1 变截面单箱单室波形钢腹板组合箱梁

1.1 基本假定

本文在推导过程中用到了如下基本假定：

(1)在加劲杆-薄板等效结构体系中，加劲杆仅承担轴力，等效薄板仅传递剪力，且忽略泊松效应的影响。

(2)忽略波形钢腹板的轴向刚度。

(3)结构处于弹性阶段。

1.2 加劲杆等效面积计算

波形钢腹板组合箱梁混凝土顶、底板的正应力σo(x)和σu(x)为

(1)

式中：M(x)为作用在截面上的弯矩；I(x)为横截面对形心轴的惯性矩；Aoe(x)、Aue(x)分别为混凝土顶板和底板的等效翼缘面积。

根据基本假定(2)，在计算I(x)时可忽略波形钢腹板的贡献[17-18]。由式(1)可得

Aoe(x)=toe(x)bo=β1(x)tobo

(2)

Aue(x)=tue(x)bu=β2(x)tu(x)bu

(3)

式中：toe(x)、tue(x)分别为混凝土顶、底板的等效翼缘厚度；β1(x)、β2(x)为系数，即

(4)

(5)

由于波形钢腹板组合箱梁的抗弯刚度基本完全由混凝土上、下翼缘板承担，因此β1(x)≈1,β2(x)≈1。在接下来的推导过程中，可令toe(x)=to(x),tue(x)=tu(x)，由此对计算结果造成的误差可忽略不计。之后，再将顶、底板等效翼缘面积集中于各加劲杆上。由图1(c)可知，加劲杆可分为两类，分别为不与腹板相交的加劲杆(1#～2#、4#～6#、8#～9#、11#～13#)和与腹板相交的加劲杆(3#、7#、10#、14#)。对于顶、底板内不与腹板相交的加劲杆的面积为

(6)

(7)

式中：i为加劲杆编号；yi-1、yi+1分别为第i-1、i+1根加劲杆距截面中心线的水平距离，其中y0=b1+b2,y5=0。

而对于与腹板相交的加劲杆，除了将顶、底板等效翼缘面积汇聚于此外，还需依据抗弯刚度等效的原则将腹板面积按比例集中于该处的加劲杆上。由于波形钢腹板对抗弯刚度的贡献可忽略不计，因此与腹板相交的加劲杆面积同样可按式(6)、式(7)计算。

上述推导过程表明，由于波形钢腹板组合箱梁具有特殊的结构形式，其加劲杆面积的计算与常规混凝土箱梁时的情形有所区别。

1.3 控制微分方程的建立

根据结构和荷载的对称性，取比拟杆等效模型的右半部分进行分析，其受力情况见图2。

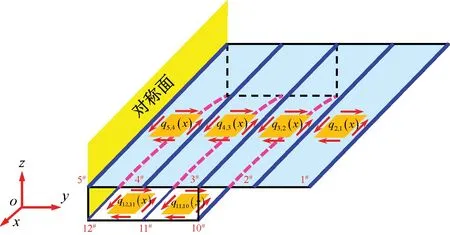
图2 比拟杆等效模型受力示意

在距自由端x处截取微梁段Δx，可建立顶板1#～5#加劲杆的平衡方程为

(8)

式中：Ni(x)为第i根加劲杆的轴力；qi+1,i(x)为第i根和第i+1根加劲杆之间薄板内的剪力流；qE(x)为与混凝土顶板交界处波形钢腹板内的水平剪力流。同时，相邻两根加劲杆之间薄板上微块的剪切角变化率可表示为

(9)

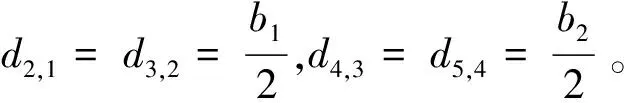
将qi+1,i(x)=Gcγi+1,i(x)toe(x)代入式(9)可得

(10)

式中：Gc为混凝土的剪切模量。

由式(10)可分别建立顶板内1#～4#四块薄板的协调方程为

(11)

同样的，对于下翼缘板，可建立关于加劲杆的3个平衡方程以及关于薄板的2个变形协调方程，但在推导过程中需考虑底板倾角的影响，限于篇幅此处不再详细说明。

1.4 波形钢腹板内剪力流大小

由式(8)可知，腹板内剪力流的大小将直接影响加劲杆轴力的计算结果，从而影响最终的剪力滞效应水平。Zhou等[19]的研究表明，与等截面时的情形所不同的是，由于变截面效应的影响，变截面波形钢腹板组合箱梁中腹板剪应力的计算需将弯矩和轴力引起的附加剪应力考虑在内。本文基于微元体平衡条件来推导变截面梁中钢腹板剪力流的计算公式。

在变截面梁上取微梁段dx进行分析，见图3(a)。其中Q(x)、N(x)分别为作用在截面上的剪力和轴力，α(x)为两端截面形心连线与水平方向的夹角，β(x)为混凝土底板底面与水平方向的夹角。由力矩平衡条件可得

(12)

微梁段横截面上距梁顶为y(x)位置处的正应力可表示为

(13)

式中：A(x)为横截面面积，在计算A(x)和I(x)时可忽略波形钢腹板的影响；yc(x)为截面形心至梁顶的距离。

在微梁段的钢腹板上以水平截面OO′截取其以上部分为分离体，对分离体进行受力分析，见图3(b)。根据分离体水平方向的平衡条件可得

图3 变截面波形钢腹板组合箱梁钢腹板剪力流计算

(14)

式中：qE(x)为与上翼缘板交界处波形钢腹板内水平剪力流；D(x)为横截面上剪力流计算点以上区域的水平合力。

根据基本假定(2)，波形钢腹板不承担轴力，D(x)为

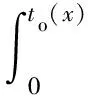
(15)

qE(x)=qQS+qME+qNS

(16)

式中：qQS、qMS和qNS分别为竖向剪力、弯矩和轴力引起的附加剪力流(单箱单室截面情况下)；Aa为等效梁的顶板横截面积；Sa(x)为Aa对截面中性轴的面积矩。

在式(16)中，变截面波形钢腹板组合箱梁中腹板内剪力流由qQS、qME和qNS三部分组成，这与等截面时的情形有着显著的区别。对于变截面简支梁及悬臂梁而言，主梁内没有轴力，此时式(16)可以简化为

(17)

1.5 边界条件

(1)简支梁

对于简支梁而言，其左、右两端部截面处顶、底板内各加劲杆的轴力为零，可得

Ni(0)=Ni(L)=0

(18)

(2)悬臂梁

对于悬臂梁而言，其自由端处顶、底板内各加劲杆的轴力为零，可得

Ni(0)=0

(19)

其嵌固端处各薄板由于受到约束而不能发生剪切变形，可得

qi,i-1(L)=0

(20)

1.6 控制微分方程的求解

传统的比拟杆法[20]首先推导得到一系列平衡方程、变形协调方程以及物理方程，再联立方程得到关于加劲杆间薄板剪力流函数的二阶微分方程组(方程组中包含5个二阶微分方程)，并采用算子解法(消去法)或样条函数逼近法进行求解。该种求解方法对于等截面梁是有效的。然而，对于变截面梁而言，由于变截面效应的影响，各加劲杆面积沿梁长方向会发生变化。因此，在建立薄板剪力流函数的二阶微分方程组时会产生关于加劲杆面积的微分形式，导致难以得到数值解。本文将联立推导得到的平衡方程、变形协调方程以及物理方程(式(8)、式(11)、式(17))，得到关于混凝土顶板内加劲杆轴力和薄板剪力流函数的一阶微分方程组(方程组中包含9个一阶微分方程)，并根据已有边界条件，采用Matlab中提供的库函数bvp4c直接进行求解。

改革开放以来，国家教育部门针对学生的运动技能评价标准及要求多次发布重要文件，力求在政策上引领教师认真教学，学生努力学习。[1]从2007年到2016年，国家连续发布了四个政策性文件，文件中明确提到了让学生掌握一至两项运动技能，这说明了青少年技能掌握与其健康成长效益之间关系密切，同时也表明“技能掌握”目标的艰难。体育界知名学者毛振明教授曾撰文指出：学生熟练掌握一项以上体育运动技能已经是“百年困境”[2]。

根据上述求解流程，采用Matlab编制了相应的求解程序。运行程序可得到顶板(底板)内加劲杆正应力沿梁长方向的分布函数，从而得到各横截面处混凝土顶、底板的剪力滞系数。

2 修正比拟杆法-单箱多室截面

接下来考虑具有单箱多室截面的变截面波形钢腹板组合箱梁，箱室数为n，横截面见图4(a)。同样地，可将该变截面梁离散为加劲杆-薄板等效模型，其中混凝土顶、底板分别等效为2n+5和2n+1根加劲杆，各杆编号见图4(b)。当箱室数量改变后，加劲杆平衡方程以及波形钢腹板内剪力流表达式均需重新进行推导，以下分别进行说明。

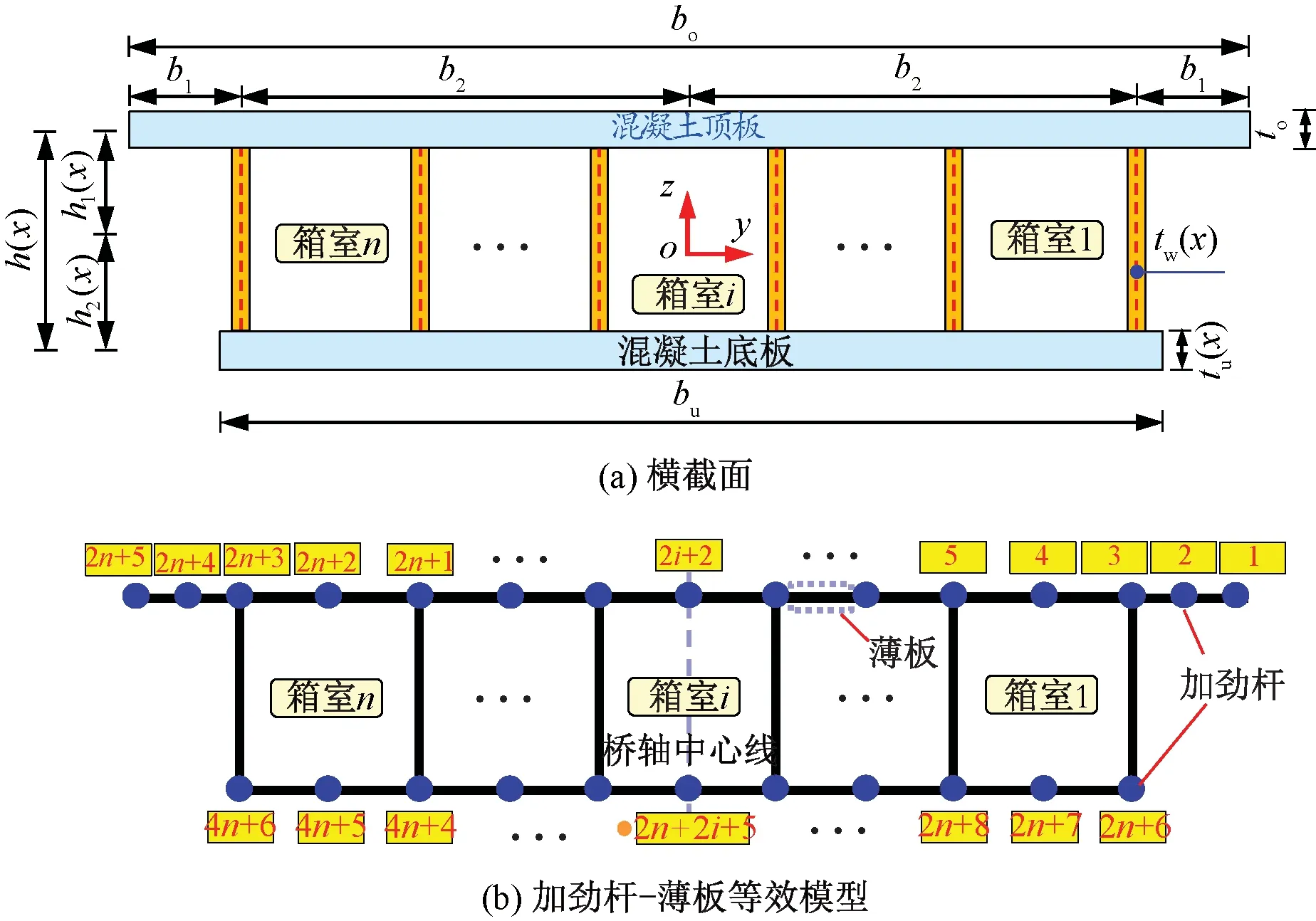
图4 单箱多室截面的比拟杆等效模型示意

2.1 加劲杆平衡方程

与单箱单室时的情形类似，取比拟杆等效模型的右半部分进行分析。顶板1#～(n+3)#((n+3)为桥轴中心线处加劲杆)加劲杆的平衡方程可表示为

(21)

由式(21)可知，当箱室数n分别为奇数和偶数时，各加劲杆平衡方程的表达式是有所区别的。主要原因在于当n为奇数时，桥轴中心线处加劲杆不与钢腹板相连，而当n为偶数时，该加劲杆与钢腹板相连，在建立平衡方程时需考虑钢腹板剪应力的影响。

2.2 波形钢腹板内剪力流大小

从单箱单室变为单箱多室后，腹板数量变为n+1。因此，钢腹板内剪力流的计算公式可修正为

qE(x)=qQM+qMM+qNM

(22)

式中：qQM、qMM和qNM分别为竖向剪力、弯矩和轴力引起的附加剪力流(单箱多室截面情况下)。

对于变截面简支梁和悬臂梁，由于主梁内没有轴力，同样可对式(22)进行简化，消除由轴力引起的附加剪力流qNM。在此基础上，建立单箱多室截面的控制微分方程，并根据已有边界条件对微分方程进行求解。

3 算例1：变截面单箱单室悬臂梁

3.1 本文理论方法验证

变截面波形钢腹板组合箱梁常采用悬臂浇筑法进行施工，在合龙前主梁一直处于悬臂状态。本算例取滁河大桥在施工过程中的最大悬臂阶段进行分析，以验证本文理论方法的适用性。为简化计算，忽略端部和跨中横隔板以及波形钢腹板内衬混凝土。单箱单室悬臂梁示意见图5。由图5(a)可知，该悬臂梁长44.8 m，梁高从3 m渐变至6.5 m，混凝土底板厚度从0.3 m渐变至0.7 m，且均按1.6次抛物线渐变。混凝土顶、底板的宽度分别为16、8 m，波形钢腹板厚度为15 mm，横截面及波形钢腹板的具体尺寸见图5(b)。混凝土及钢材均假定为线弹性材料，两者弹性模量分别为34 500、210 000 MPa，泊松比分别为0.2和0.3。除考虑结构自重外，在悬臂梁端部施加2 000 kN竖向集中荷载来模拟挂篮荷载。

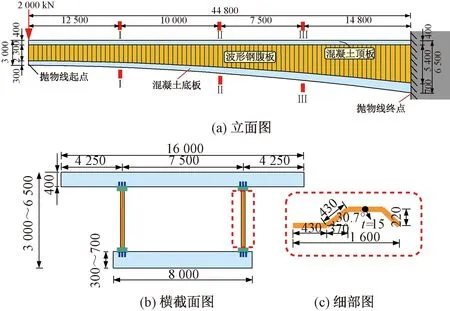
图5 单箱单室悬臂梁示意(单位：mm)

采用Ansys建立算例梁的空间实体有限元模型，见图6。混凝土顶底板和波形钢腹板分别采用Solid185和Shell181单元进行模拟。需要说明的是，模型中采用MPC法来实现混凝土翼缘板与波形钢腹板之间的连接，以确保实体单元与壳单元之间弯矩的传递[21]。为保证计算精度，采用映射法划分网格。

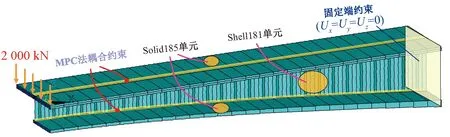
图6 算例梁有限元模型(1/2模型)

修正比拟杆法及实体有限元模型的Ⅰ-Ⅰ、Ⅱ-Ⅱ和Ⅲ-Ⅲ截面处混凝土顶、底板正应力结果见图7，其中Ⅰ-Ⅰ、Ⅱ-Ⅱ和Ⅲ-Ⅲ截面分别距悬臂端12.5、22.5、30 m。由图7可知，各计算截面处的理论结果与有限元结果均吻合很好，最大误差仅为1.36%，由此证明了本文所提出理论方法的有效性。同时，图7中结果还表明，在结构自重以及端部集中荷载共同作用下，截面Ⅰ-Ⅰ的混凝土顶板和底板均出现负剪力滞现象，顶、底板与钢腹板交界处的剪力滞系数分别为0.98和0.99；而截面Ⅱ-Ⅱ和截面Ⅲ-Ⅲ的顶、底板则呈现出十分微弱的正剪力滞效应，最大剪力滞系数仅为1.004。

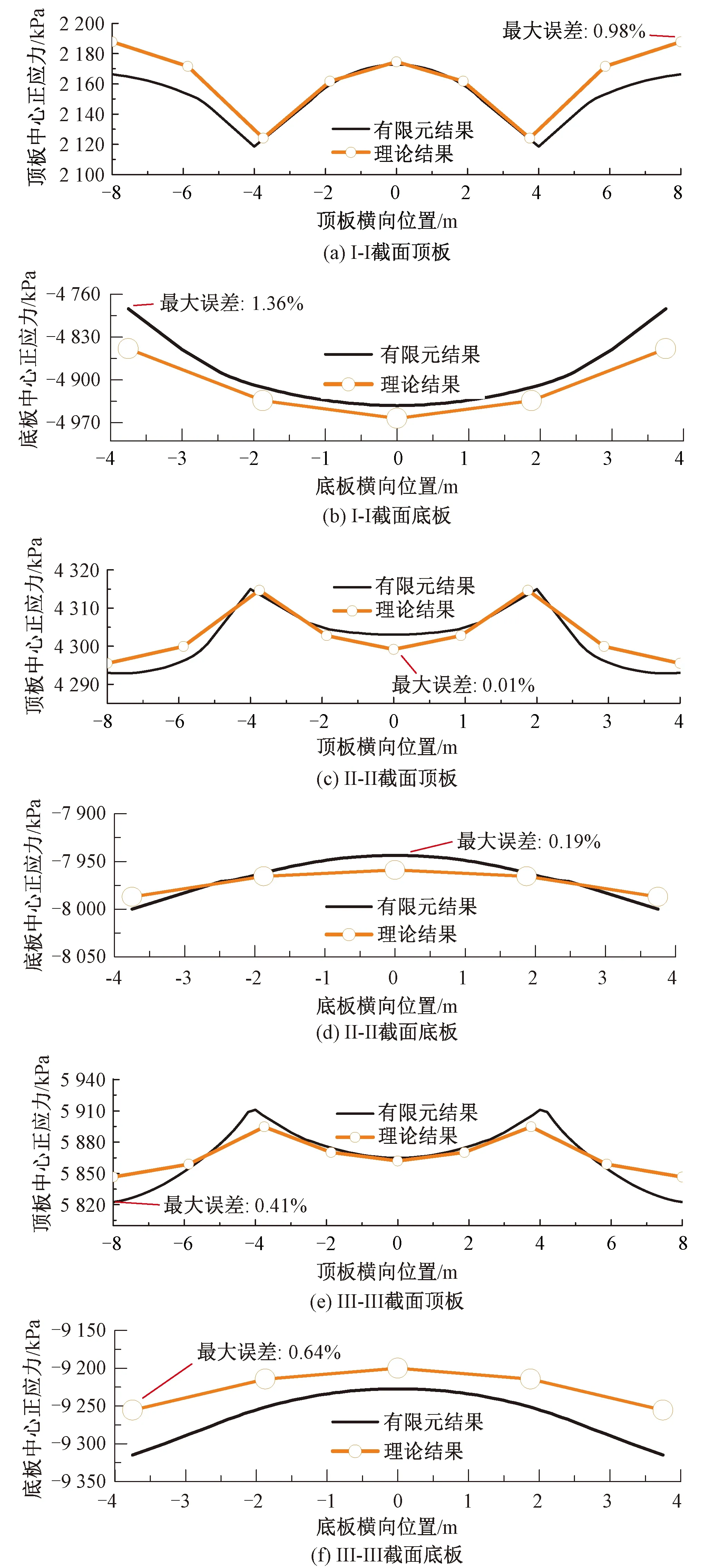
图7 有限元结果和理论结果对比-算例1

3.2 加劲杆个数对计算结果的影响

本文理论模型在推导时将混凝土顶、底板分别等效为9根和5根加劲杆。为探讨等效加劲杆个数对本文理论方法计算精度的影响，将混凝土顶板分别等效为5根和13根加劲杆，对应的混凝土底板则分别等效为3根和7根加劲杆，见图8。然后，对本文理论方法进行重新推导。将混凝土顶板等效为5根、9根和13根加劲杆时的情形分别称为五杆、九杆和十三杆修正比拟法。

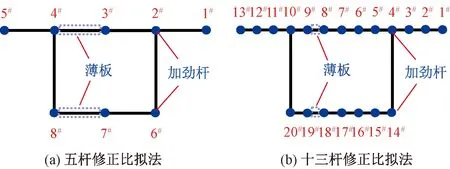
图8 五杆及十三杆修正比拟法

以3.1小节中单箱单室悬臂梁为例，将五杆、九杆和十三杆修正比拟法以及有限元模型给出的Ⅱ-Ⅱ截面处混凝土顶板正应力结果列于图9。由图9可知，由五杆、九杆和十三杆修正比拟法计算得到的理论结果均十分接近(最大仅相差0.08%)，且均与有限元结果吻合良好。尽管修正比拟杆法的计算精度对加劲杆个数不敏感，但加劲杆个数越多能更好地反映正应力沿横向的分布规律。一般而言，将混凝土顶、底板分别等效为9根和5根加劲杆时即可满足要求。

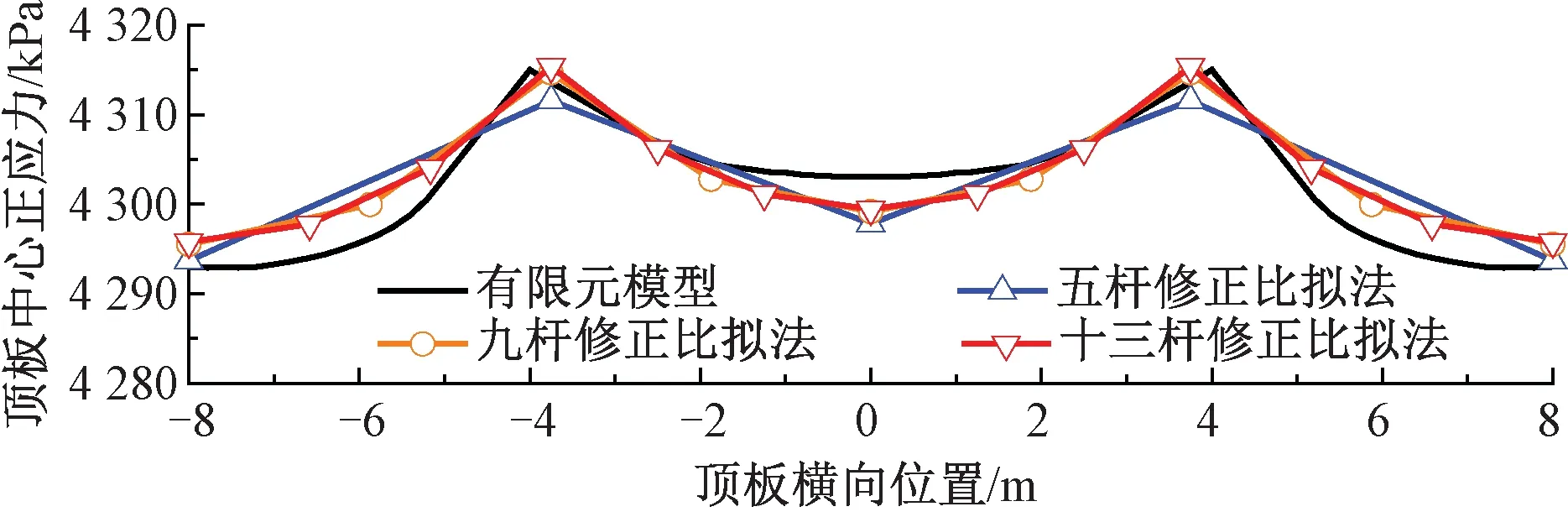
图9 加劲杆个数对计算结果的影响

4 算例2：变截面单箱三室悬臂梁

为验证本文理论方法在单箱多室情况下的适用性，将算例梁1改为单箱三室截面，见图10，主梁的其余结构布置形式、边界条件以及材料特性等均不变。在悬臂梁端部施加2 000 kN竖向集中荷载，同时考虑结构自重的影响。采用Ansys建立了该变截面单箱三室悬臂梁的空间实体有限元模型。

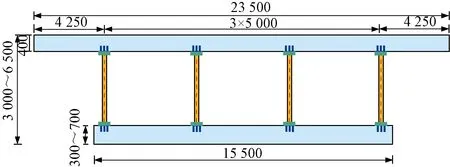
图10 单箱三室悬臂梁横截面图(单位：mm)

将修正比拟杆法及有限元模型的Ⅰ-Ⅰ、Ⅱ-Ⅱ和Ⅲ-Ⅲ截面处混凝土顶板正应力结果见图11，上述三个截面的位置与算例1中一致(见图5)。由图11可知，各截面的理论结果与有限元结果均吻合较好，最大误差仅为1.77%，表明本文理论方法同样适用于单箱多室情形。由图11可知，在端部集中荷载和结构自重共同作用下，变截面波形钢腹板组合箱梁从悬臂端的负剪力滞效应逐渐过渡到固定端的正剪力滞效应，悬臂梁中部(截面Ⅱ-Ⅱ附近)为正、负剪力滞的过渡区域，剪力滞效应十分微弱。

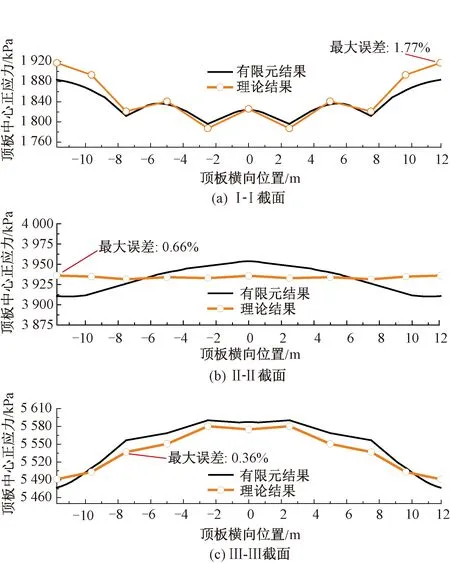
图11 有限元结果和理论结果对比-算例2

5 参数分析

变截面箱梁的剪力滞效应受诸多因素影响，主要包括宽跨比、梁高比和荷载形式等。基于本文提出的修正比拟杆法，采用参数分析来检验上述因素对变截面波形钢腹板组合箱梁剪力滞效应的影响规律。由于变截面梁桥在施工阶段基本处于悬臂状态，因此选取算例1中的悬臂梁进行分析，沿梁长施加200 kN/m均布荷载(为简化计算，未考虑结构自重)。用混凝土顶板与波形钢腹板交界处的剪力滞系数大小λe来表征剪力滞效应的程度，λe大于或小于1分别表示正、负剪力滞效应。为防止各因素间的相互干扰，在分析某单个因素的影响规律时，保持其他因素不变。

5.1 宽跨比

维持该变截面梁的跨度不变，宽度(两波形钢腹板的中心间距)分别取5.5、7.5、9.5、11.5 m，对应的宽跨比分别为0.12、0.17、0.21、0.25。宽跨比对λe沿梁长分布的影响规律见图12。由图12可知，随着宽跨比的增加，变截面波形钢腹板悬臂箱梁的剪力滞效应更突出。具体而言，当宽跨比从0.12提高到0.25时，离悬臂端7.5 m处的λe值从0.72降到了0.51，降幅为29%(需要说明的是，对于负剪力滞效应来说，λe值越小表明剪力滞效应更显著)。但宽跨比的变化并不会改变正、负剪力滞区段分割点的位置。

图12中靠近悬臂端区段内λe值为负数。该现象表明在该区段内，与波形钢腹板交界处的混凝土顶板正应力值与采用初等梁理论计算得到的正应力值符号相反。

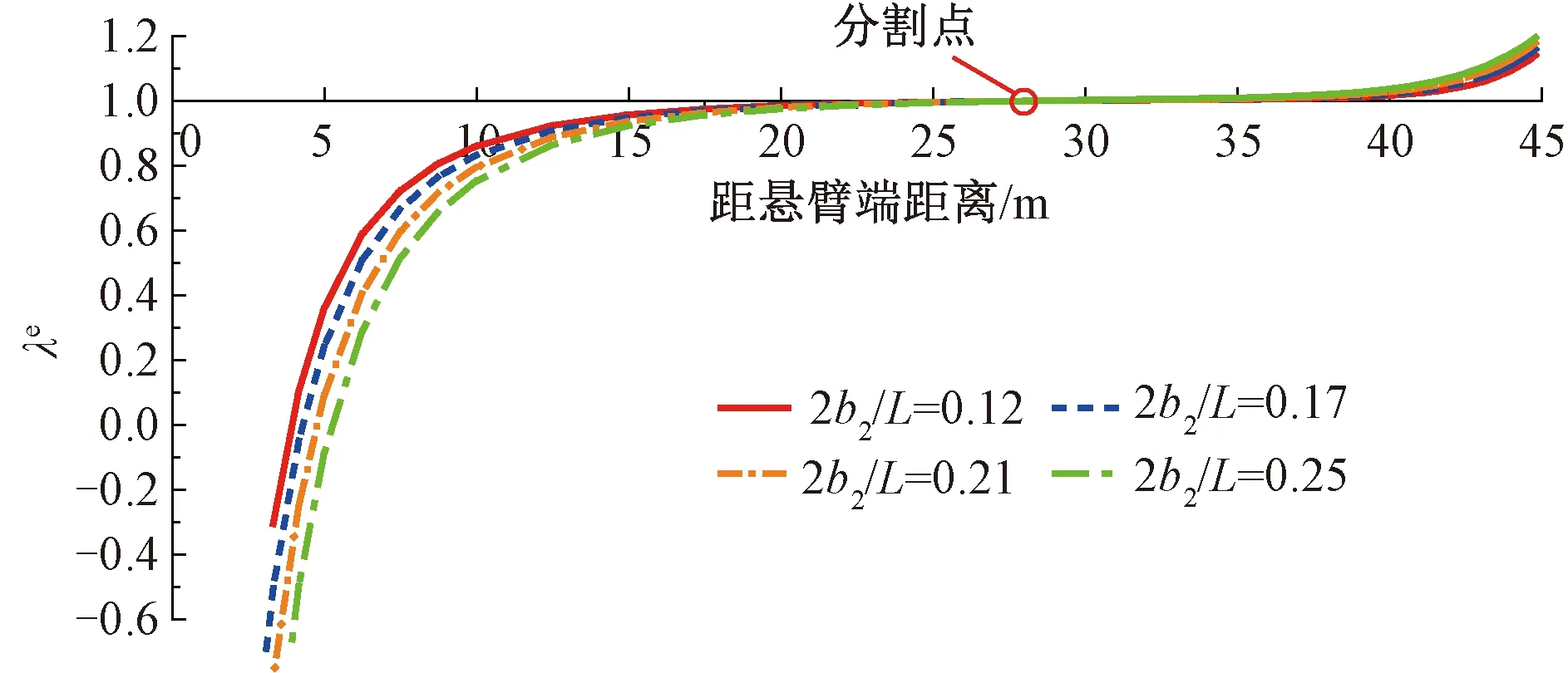
图12 宽跨比对剪力滞效应的影响

5.2 梁高比

维持固定端梁高为6.5 m不变，取悬臂端梁高分别为1.5、3.0、4.5、6.5 m，对应的梁高比ξ(悬臂端梁高与固定端梁高之比)分别为0.23、0.46、0.69、1.0。需要说明的是，梁高比为1.0即等截面梁的情形。将不同梁高比情况下λe沿梁长的分布规律见图13。由图13可知，随着梁高比的增加，变截面波形钢腹板悬臂箱梁的剪力滞效应也随之增强，等截面梁的剪力滞行为比对应的变截面梁更显著。图13中结果还表明，随着梁高比的增加，正、负剪力滞区段分割点越靠近固定端，即负剪力滞效应所占区段增长。

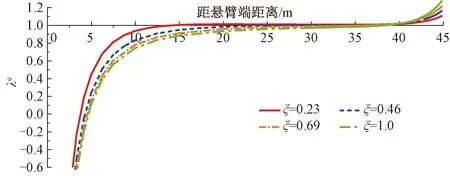
图13 梁高比对剪力滞效应的影响

5.3 荷载形式

为探讨不同荷载形式对变截面波形钢腹板悬臂箱梁剪力滞效应的影响规律，考虑四种常用荷载，分别为悬臂端集中荷载(2 000 kN)、均布荷载(200 kN/m)以及两种三角形分布荷载(最大荷载集度为400 kN/m，见图14。不同荷载作用下λe沿梁长的分布规律见图15。由图15可知，荷载形式不仅会对该组合箱梁剪力滞效应产生显著影响，同时也会改变正、负剪力滞区段分割点的位置。具体来说，由荷载产生的竖向剪力朝固定端增加得越迅速，则引起的剪力滞效应越显著，且正、负剪力滞区段分割点的位置越靠近固定端。就本算例而言，在端部集中荷载作用下，竖向剪力朝固定端增加速率为0，因此该荷载工况下悬臂梁的剪力滞效应最弱，最大剪力滞系数仅为1.09，而三角形分布荷载造成的剪力滞效应则最为显著。此外，对于三角形分布荷载2、均布荷载和三角形分布荷载1而言，三种荷载工况下正、负剪力滞区段分割点离固定端的距离分别为22.4、16.8、8.1 m，与其竖向剪力朝固定端增加速率的快慢相一致。端部集中荷载作用下混凝土顶板内仅出现正剪力滞行为，可视作正、负剪力滞区段分割点无限靠近固定端。

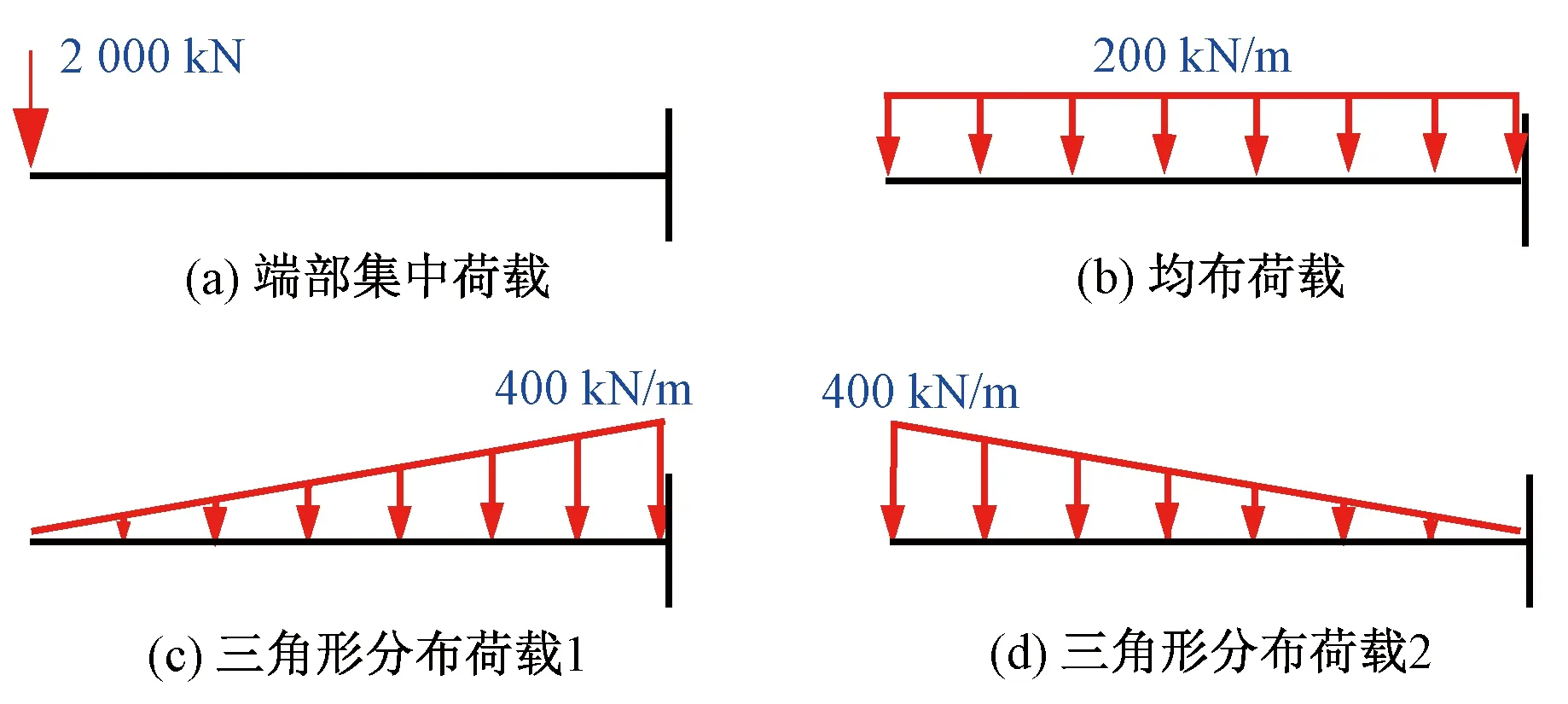
图14 四种不同荷载形式

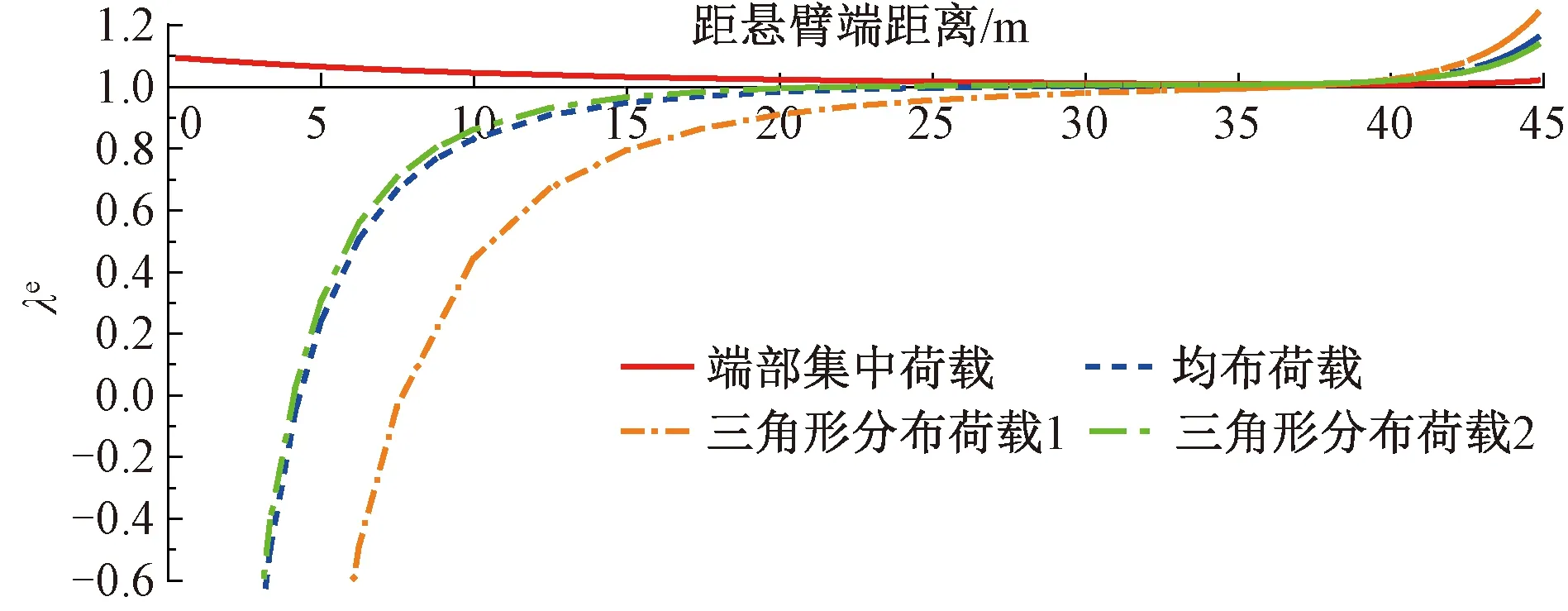
图15 荷载形式对剪力滞效应的影响

6 结论

针对传统比拟杆法仅能分析等截面梁剪力滞效应的不足，本文在充分考虑变截面波形钢腹板组合箱梁结构和受力特性的基础上，对传统比拟杆法进行了重新推导，提出了用于分析该结构剪力滞效应的修正比拟杆法，并采用有限元手段验证了所提出理论方法的适用性。然后，完成了参数分析来探讨不同因素对变截面波形钢腹板悬臂箱梁剪力滞行为的影响规律。主要结论如下：

(1)数值算例结果表明，本文提出的修正比拟杆法适用于单箱单室和单箱多室截面，且具有良好的精度，为分析变截面波形钢腹板组合箱梁的剪力滞效应提供了一种有效且便捷的途径。

(2)等效加劲杆个数对修正比拟杆法的计算精度影响较小，但加劲杆个数越多能更好地反映正应力沿横向的分布规律，建议将混凝土顶、底板分别等效为9根和5根加劲杆。

(3)增加宽跨比或梁高比会引起更严重的剪力滞效应。宽跨比的变化并不会改变正、负剪力滞区段分割点的位置；但随着梁高比的增大，正、负剪力滞区段分割点会更加靠近固定端，负剪力滞区段会增长。

(4)对于不同的荷载形式，由荷载产生的竖向剪力朝固定端增加得越迅速，引起的剪力滞效应越显著，且正、负剪力滞区段分割点的位置越靠近固定端。