桥上钢弹簧浮置板的结构振动声辐射特性研究

张晓芸，张小安，王开云，石广田，黄志丹

(1.兰州交通大学 机电工程学院， 甘肃 兰州 730070；2.西南交通大学 牵引动力国家重点实验室列车与线路研究所， 四川 成都 610031)

城市轨道交通能够极大的提高居民的日常出行效率，解决城市交通拥堵等诸多问题。而城市轨道交通主要修建于城市繁华地带，在运营时常会引起很多环境问题，主要包括环境振动、噪声以及电磁辐射等。其中以噪声问题最为突出，包含轮轨噪声、空气噪声、集电噪声等，并且当振动能量较大时也能引起周围建筑物振动辐射噪声。当列车在高架线路运行时，将会引起桥梁基础结构振动进而辐射噪声，导致此线路上的噪声整体水平更高。目前关于城市轨道交通所引起的环境问题，主要集中在环境振动方面的研究，即如何降低列车运营时对周围结构的振动影响。因此针对轨道结构各部件均进行了很多减振措施的研究与研发工作，例如钢轨阻尼器、钢轨动力吸振器(钢轨)，科隆蛋扣件、GJ-Ⅲ扣件(扣件系统)、弹性支撑块式轨道、梯形轨道(轨枕)、橡胶浮置板轨道、钢弹簧浮置板轨道(道床)等多种减振产品，现已广泛应用于城市轨道交通的建设中。

在上述所提到的多种减振产品中，以钢弹簧浮置板的减振效果最为显著[1]，目前在城市振动敏感区域已被广泛铺设。关于浮置板轨道的研究最早始于1977年，Grootenhuis[2]首先研究了几种用于减小轨道交通振动传播的浮置板结构。Cui等[3]采用柔度法对简谐激励下的浮置板轨道和普通整体轨道的动力学响应以及减振效果进行了研究，表明两者相比浮置板的减振效果更好。李增光等[4]建立了符合轨道动态特性的力学模型，采用动柔度方法分析了浮置板的隔振性能及其影响因素。Lombaert等[5]通过建立三维数值模型，以轨道-土壤间的相互作用和土壤属性对浮置板轨道在自由场中的减振效果进行了研究。Schillemans[6]对浮置板轨道的减振效果进行了评估，指出浮置板轨道具有良好的减振效果。韦红亮等[7]通过有限元法和现场试验的方法对高架桥上的钢弹簧浮置板轨道结构的减振特性进行了分析。

除了研究浮置板轨道的隔振性能外，很多学者也对浮置板在服役过程中的动力学性能进行了大量的研究工作。Zhai等[8]基于车辆-轨道耦合动力学理论，系统研究了钢弹簧浮置板轨道在时域和频域内车速、浮置板长度、厚度以及钢弹簧的分布等因素对钢弹簧支点力的影响。Shi等[9]采用格林函数法建立了车辆-钢弹簧浮置板-桥梁耦合动力学模型，对整体系统中高频段的动力学响应以及影响参数进行详细的研究。王建伟等[10]对钢弹簧浮置板轨道结构中的钢弹簧隔振器刚度和阻尼的频率和幅值之间的依赖性进行了试验研究。刘维宁等[11]对钢弹簧浮置板的低频特征进行了现场测试，研究了钢弹簧浮置板的轨道弹簧刚度、支承间距的变化对低频振动的影响。

此外，很多学者也对钢弹簧浮置板轨道结构进行了优化和改进，以解决浮置板轨道结构自身问题以及提高其相关性能。韦凯等[12]通过建立车辆-钢弹簧浮置板轨道垂向耦合动力学模型，以扣件系统中的刚度和阻尼作为参数，分析了钢弹簧浮置板轨道在频域内的随机振动特性。张龙庆等[13]以浮置板轨道结构为对象，在模态分析的基础上确立了浮置板上附加动力吸振器的最优刚度、阻尼和附件位置，同时对动力吸振器在不同质量比下的吸振特性以及低频振动控制特性进行了分析。杨吉忠等[14]以短型钢弹簧浮置板轨道为基础，建立了一种被动式减振轨道结构，指出此种轨道结构可以有效抑制13 Hz附近的振动。

在高架线路上铺设钢弹簧浮置板轨道，最主要的目的是为了减小传递至桥梁结构的振动能量，同时也能够降低桥梁结构辐射的噪声。但相关的研究表明，虽然钢弹簧浮置板轨道减小了桥梁结构的振动，却反而增大了其自身的振动。冯读贝等[15]基于车辆-轨道耦合动力学理论与有限元法，对高架简支箱梁上的非减振轨道，钢弹簧浮置板轨道以及被动式动力减振浮置板轨道下的低频振动特性进行了研究，指出在15～30 Hz内钢弹簧浮置板轨道是通过增大自身振动得以降低桥梁的振动。刘小强等[16]对32 m简支箱梁上钢弹簧浮置板轨道结构的垂向振动传递特性进行了研究，同样得出与整体无砟轨道相比，在低频段浮置板轨道虽然能降低桥梁的振动，但自身反而增大。文献[7]也得到了类似的研究结果。

综上所述，桥上铺设的钢弹簧浮置板轨道自身振动增大，很可能增强其自身的声辐射。因此本文基于列车-轨道-桥梁相互作用理论对钢弹簧浮置板的动力学响应进行求解，以钢弹簧浮置板轨道的动力学响应作为输入，采用声学边界元法对钢弹簧浮置板的结构声辐射进行分析。系统研究了这种具有良好减振效果的轨道结构自身的声辐射问题，为既具有良好减振效果，又辐射低噪声的环保型减振轨道结构的研制提供一定的理论依据。

1 数值分析

轨道交通中列车运行于高架线路，整体系统包含车辆子系统、轨道子系统以及桥梁子系统，三者的动力学方程可分别表述为

(1)

(2)

(3)

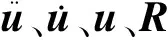
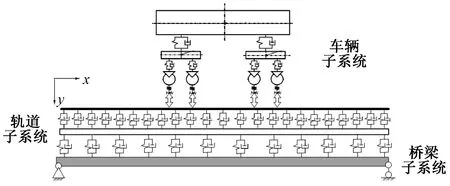
图1 车辆-轨道-桥梁动力相互作用示意

首先建立车辆-浮置板轨道耦合动力学模型，以美国铁路线路不平顺六级功率谱密度为激励，采用翟婉明院士[20-21]提出的显示积分方法计算轮轨相互作用力。线路基础结构则采用三维有限元模型，包括钢弹簧浮置板轨道以及32 m箱梁桥；其中箱梁桥有限元模型采用Shell63单元进行模拟，弹性模量、泊松比及密度分别为38 GPa、0.2和2 500 kg/m3，钢弹簧浮置板轨道的有限元模型及动力学参数见图2和表1，扣件和钢弹簧间距取0.625 m，浮置板的长、宽、高分别为25.2、2.7、0.25 m；将轮轨力作为移动荷载施加到线路基础结构有限元模型对其动力学响应进行求解，所得结果可为后续声学求解提供准确的声学边界条件。

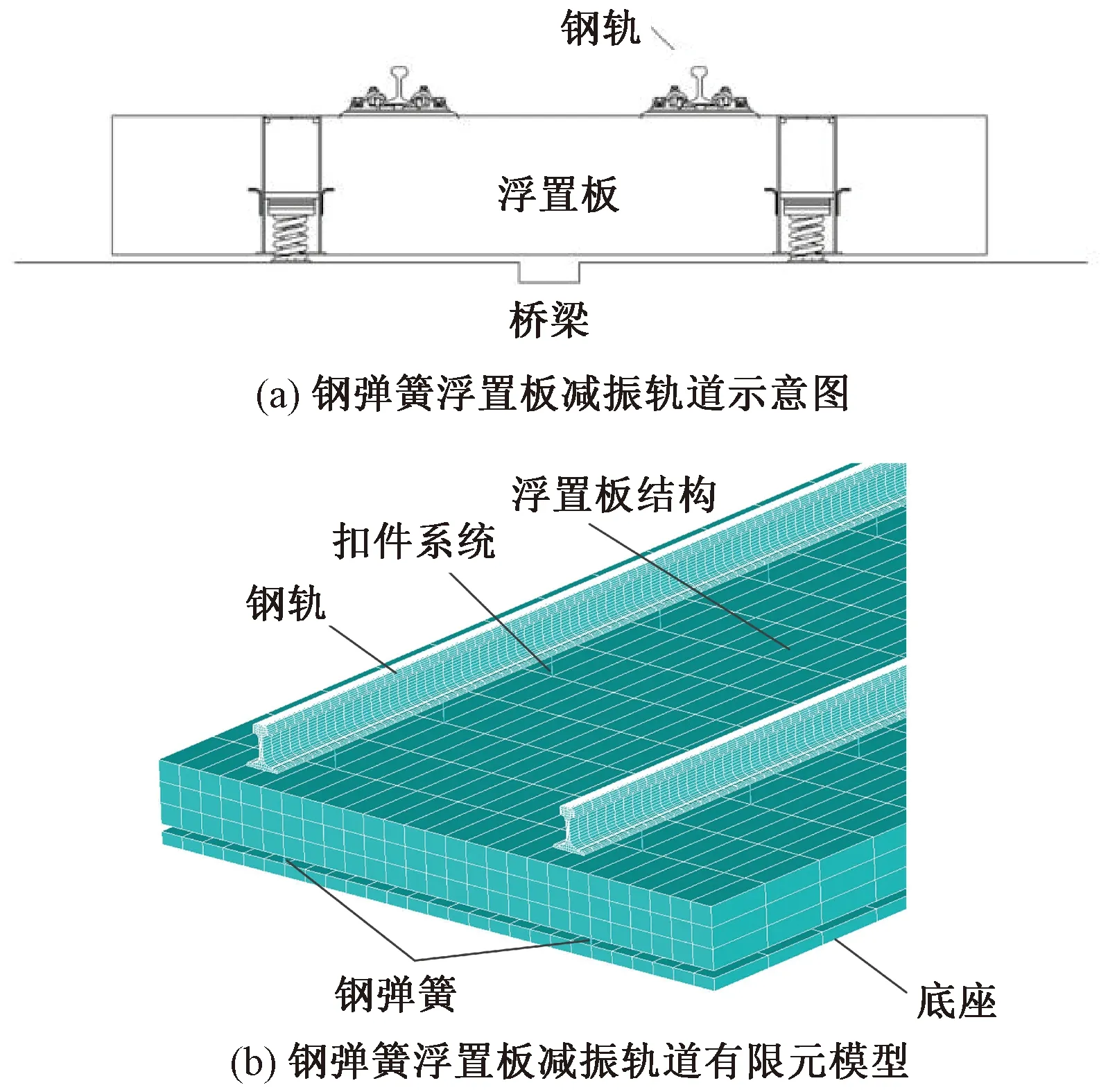
图2 桥上钢弹簧浮置板减振轨道

表1 轨道有限模型的单元类型及动力学参数

利用边界元法求解结构声辐射问题时首先需要满足波动方程、Neumann边界条件以及Sommerfeld辐射条件。对于浮置板结构，可采用直接边界元法，即利用空间的格林函数获得流体域声场中的Helmholtz积分方程，即

(4)

式中：p为声压；vn为结构边界振动法向速度；k=ω/c为波数，ω为圆频率，c为声速；i为虚数单位；ρ0为流体密度；r=|X-Y|；X为结构表面上的任意一点；Y为声场中任意点；A为结构表面积；β为法向矢量与矢径r的夹角。

结构经过单元划分后，结构振动表面的节点边界量可利用形函数表示，并利用每个节点作为源点离散Helmholtz积分方程，即可获得结构表面的声压向量与法向振速的关系为

Qpb=Pvb

(5)

式中：Q和P为对称的复数满秩矩阵；pb和vb分别为边界节点声压和法向速度向量。

由式(5)得

pb=Zvn

(6)

式中：Z=Q-1P为结构振动时的声阻抗矩阵。再利用Helmholtz积分方程可得外声场的声压[22]

p(Y)=Mp+Nvn

(7)

式中：M和N为求解外场点声压时的影响矩阵。

2 钢弹簧浮置板轨道振动声辐射分析

2.1 浮置板结构振动声辐射特性分析

选取浮置板结构中心位置作为研究对象，对计算获得的浮置板中心点时域和频域振动加速度响应进行分析，见图3。由图3可知，在低频段内(0～150 Hz)，浮置板结构的振动密集；振动最为剧烈的主振频段为210～235 Hz，最大值可达2.7 m/s2；并且在425～475 Hz也有较小浮动的振动。

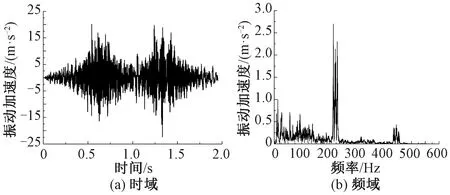
图3 浮置板中心点垂向振动加速度响应

以浮置板结构为中心，选取跨中左右各25 m、上下各10 m的区域作为浮置板结构声辐射的研究对象。研究声场场点的选取见图4，场点的间隔为1 m。

浮置板的声辐射功率见图5，由图5可知，在浮置板的低频主振频段声辐射最强，是由于剧烈的振动激发浮置板结构辐射噪声，这也是结构辐射噪声的一般特性。由振动特性可知，425～475 Hz频段内的振动幅值与150 Hz以下的低频段相近，但在较低频段内的声辐射更强。由声场中不同场点的声压可知，与浮置板处于水平位置的声压最小，远场上方次之；在浮置板正上方区域的声压最大。

远场区域的声压，即SF1、SF2以及SF3的声压频谱曲线见图6，由图6可知，主振频段与其他小振幅振动区段的声压级极为接近，因此剧烈的振动并不是决定远场区域声辐射的主要因素。由于所选的声场区域上下对称，浮置板结构处于中心位置，因此SF1和SF3的声压基本一致。另外在同一垂向声场，在浮置板水平方向上的场点声压远小于其他声场。

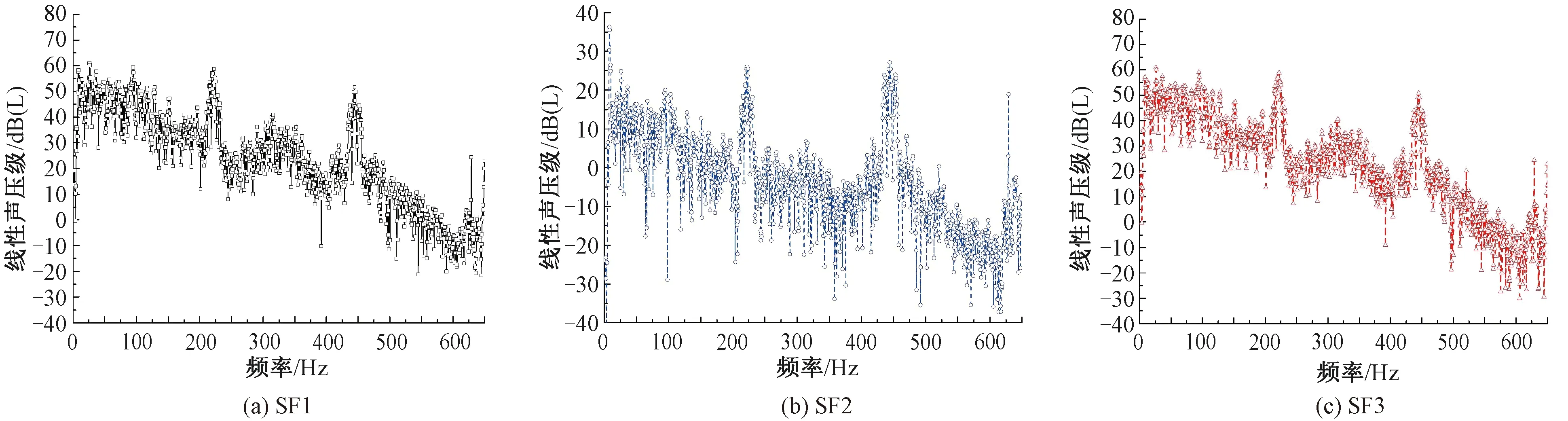
图6 远场区域声辐射特性

如图7所示，浮置板结构的正上方区域，在同一场点主振频段与0～150 Hz低频段所辐射的声压相近，并且这两个频段的声压均高于425～475 Hz。正上方声场的声压随着距离增大而逐渐减小，尤其是在0～150 Hz最为明显，声压的减小幅度也逐渐变小，间隔2 m依次减小2.2、1.6、1.4、1.2 dB。

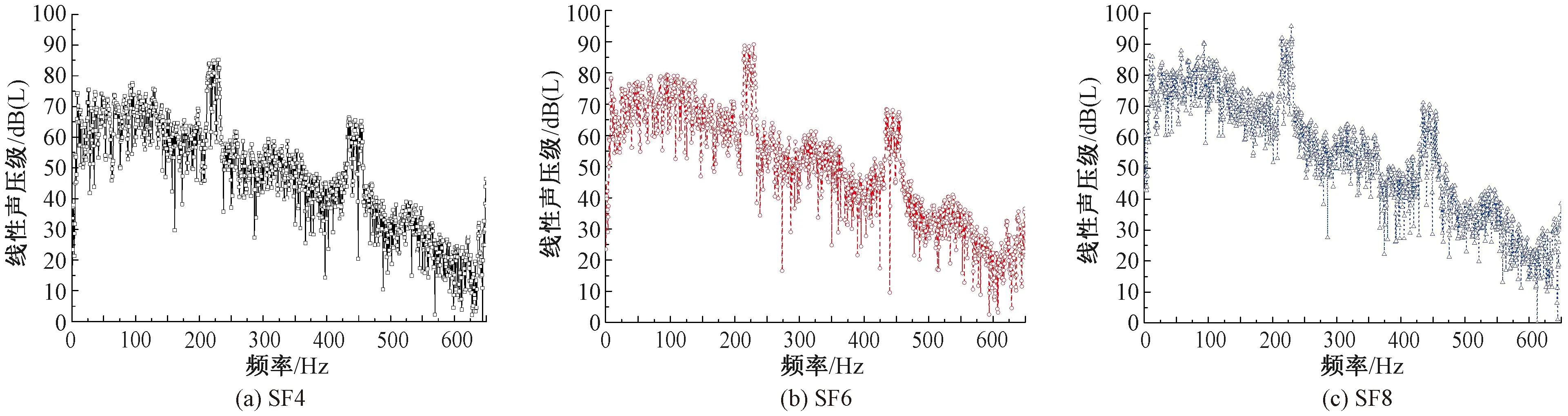
图7 正上方区域声辐射特性

2.2 浮置板结构振动声辐射机理研究

为了进一步探究浮置板结构的振动声辐射，利用上述正上方区域声压的分析与其振动加速度云图相结合对其声辐射特性做进一步研究。浮置板在外激励作用下部分频率点的振动加速度云图见图8。

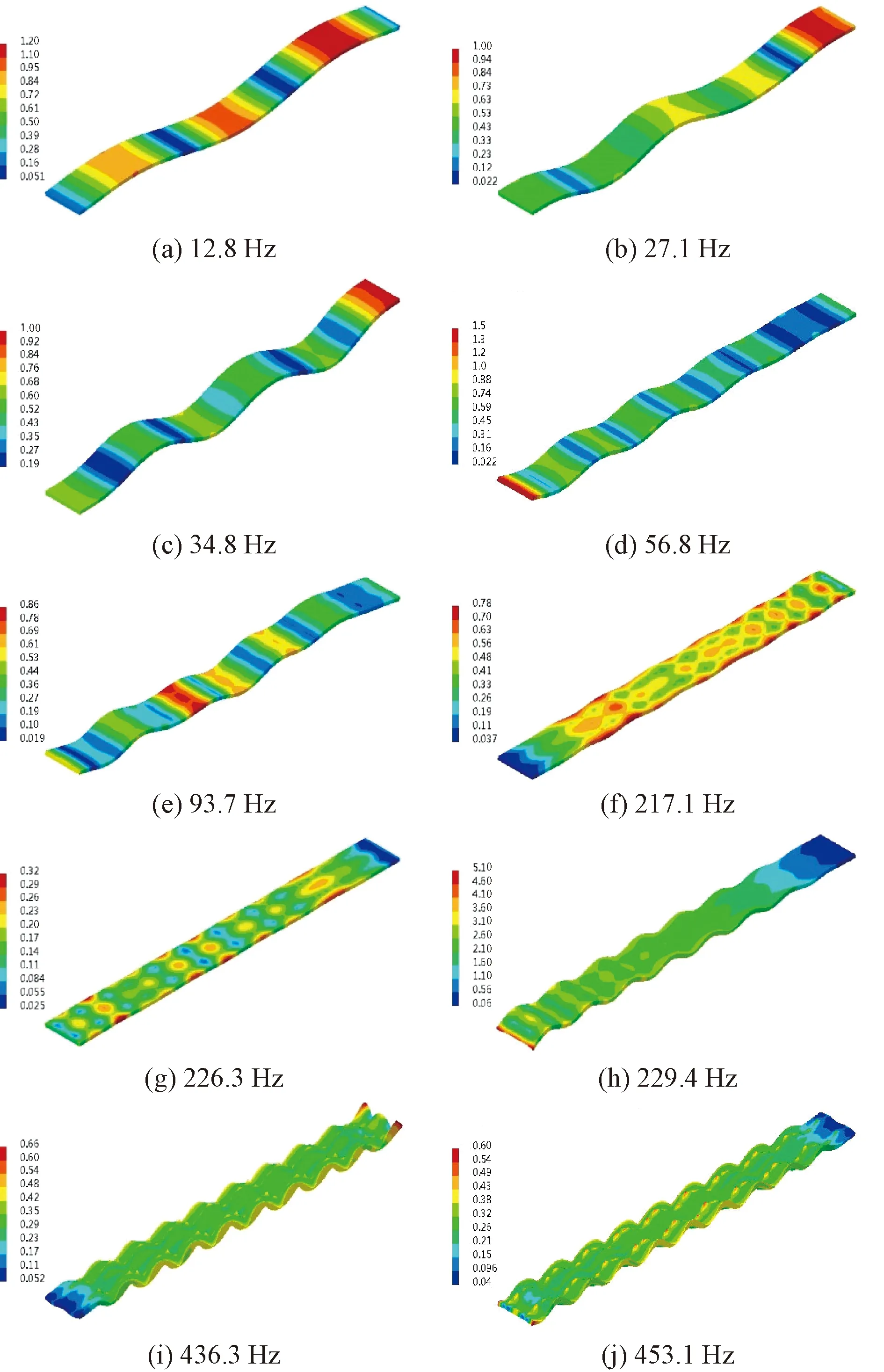
图8 钢弹簧浮置板结构在外激励作用下的振动加速度云图(单位：m/s2)

由图8可知，钢弹簧浮置板结构的振动形式主要体现为纵向上的整体弯曲振动以及局部振动。在不同的频率下所占据的地位不同，在某些频率下则两者共同作用。不同频率下的浮置板结构的振动形式、振动加速度幅值以及场点SF8的声压见表2。

由表2可知，浮置板结构的整体弯曲振动是影响其中低频段声辐射的主要因素，当整体振动的幅值较大时(229.4 Hz)，浮置板向外辐射的声压较大；浮置板结构的声辐射在0～150 Hz和210～235 Hz的声压幅值接近；浮置板的部分振型及其振动加速度云图见图9和图10。由图9和图10可知，在频率较低时，浮置板的振型与外激励下的振动形式吻合度较高，并且固有频率与振动频率相近，表明浮置板在此频段容易发生共振现象，并由此增强了其声辐射能力，因此在低频段的声辐射能力与主振频段相比也能够辐射很强的声波，均高于425～475 Hz。为了进一步证实上述结论，进一步分析17.4 Hz时浮置板结构的振动声辐射特性，浮置板中心点的振动加速幅值为0.05 m/s2，但SF8处的声压为63.4 dB；在210～235 Hz频段，整体振动时的声辐射强于局部振动；如216.1 Hz与217.1 Hz相比较，两者的振幅分别为0.58、0.50 m/s2，声压分别为78.2、81.0 dB。

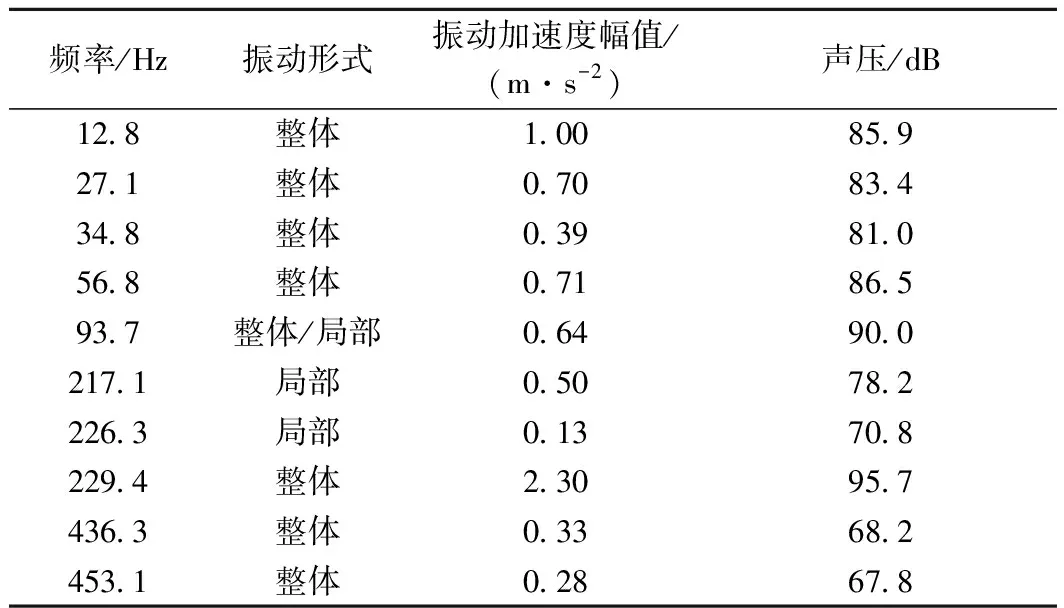
表2 声场场点SF8振动声辐射特性

图9 钢弹簧浮置板结构振动加速度云图(单位：m/s2)

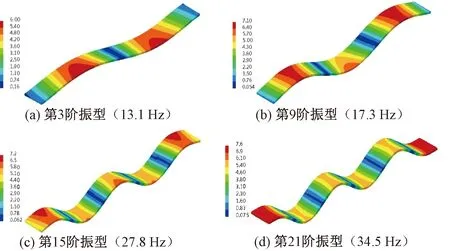
图10 钢弹簧浮置板结构的部分振型位移云图(单位：mm)

2.3 整体与局部振动特性对声辐射的影响

由浮置板的声辐射规律可知，由于未考虑声波在传播过程中反射和衍射等边界条件，浮置板结构的声辐射在垂向上沿浮置板结构上下对称，向上部和下部区域逐渐扩散，随距离的增加而逐渐减小，在水平位置的声压最小；频率较低时浮置板的声辐射规律较为规则，但随着频率的增加而变得复杂；由其振动特性可知，在频率很低时，浮置板的整体弯曲振动占主导地位，局部振动特性的影响较小；而随着频率的增大，局部与整体振动特性共同作用，导致浮置板结构的声辐射规律变得更加复杂。浮置板的声辐射规律也印证了图6中所体现的在浮置板水平方向声场的声压较小的原因。

低频时的浮置板垂向上的辐射声压随距离的增加而逐渐减小，与理想声源的声辐射类似；而在主振频段以及中频段，由于浮置板的局部振动特性也逐渐体现，导致其声辐射并不遵循理想声源的辐射规律向外辐射声波，见图11。

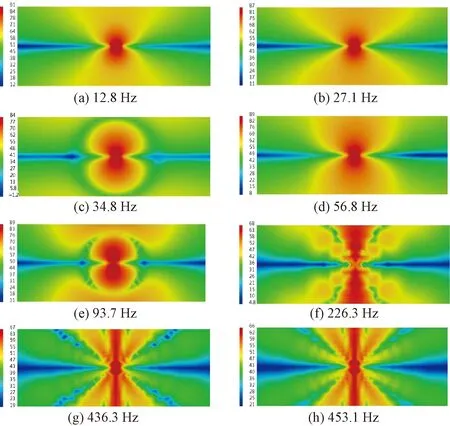
图11 钢弹簧浮置板的声辐射规律(单位：dB)

由图8和图11可知，随着频率的增大局部振动对其声辐射的影响也同时增强；浮置板结构的整体振动与局部振动相比，前者对其声辐射强度的影响更大，而对其辐射规律的影响却与之相反。对不同频率下的声辐射规律对比可知，当浮置板结构的振动特性表现为完全的整体弯曲振动时，其结构声辐射的规律较为规则；当整体和局部振动特性共同作用时则变得逐渐复杂；局部振动占主导地位的声辐射规律最为复杂。由浮置板振动特性可知，浮置板结构在纵向上呈两列弯曲振动，对斜上方区域声压的影响明显增强。

3 结论

本文通过建立相关的理论模型对桥上钢弹簧浮置板结构的声辐射机理及其特性进行了详细的分析。主要结论如下：

(1)建立钢弹簧浮置板轨道的三维有限元模型，才能很好地研究浮置板结构的整体和局部振动特性。

(2)浮置板在中低频段的振动也十分明显，主要以纵向弯曲振动为主，同时存在局部振动特性，并且局部振动特性并不是均匀的分布；浮置板在主振频段不以规则的同幅值正弦形式发生弯曲振动，其幅值呈逐渐递增或递减。

(3)钢弹簧的浮置板结构在主振频段其声辐射能力最强，在较低频段内也有很强的声辐射。浮置板在自由声场中，在其水平位置的声压最小，远场上方次之。浮置板正上方区域的声压最大，声压随着距离增大而逐渐减小，尤其是在0～150 Hz表现的最为明显，声压的减小幅度逐渐变小。

(4)浮置板结构的整体弯曲振动是其声辐射的主要因素，在频率较低时容易发生共振现象增强其声辐射能力。

(5)自由声场中浮置板结构的声辐射在垂向声场上是对称的，向上部和下部区域逐渐扩散；频率较低时浮置板结构的声辐射规律较为规则，但随着频率的增加逐渐变得较为复杂；当浮置板结构的整体弯曲振动占主导地位时声辐射较为规则，局部与整体振动特性共同作用时其声辐射规律变得复杂。

此外，由于列车通过时形成的声源众多，在对混凝土轨道结构进行声辐射的测试过程中很难对其进行区分。因此针对混凝土轨道结构自身声辐射的现场测试技术有待进一步的研究。