基于假设分布的重载货车关键结构剩余寿命预测方法

朱 涛，尹敏轩，王 超，肖守讷，杨 冰，阳光武

(西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

我国铁路货车现有的检修制度以日常检查(列检)、定期检修(段修、厂修)的计划预防修为主，虽能保证列车安全运行，但存在过度检修现象，造成检修成本的浪费。近年来，基于状态监测数据的检修模式[1-2]由于其前瞻性、检修效率高、安全可靠等特点，被广泛应用于能源、航空航天、轨道交通等工业领域[3-5]。状态修可根据先进的状态监测和诊断技术提供铁路货车状态信息，根据对设备实际状态的评估和未来预期，基于运行维护最优化原则确定维护介入时间点及相应的维护措施，具有良好的经济效益和发展前景[6-9]。

重载铁路货车零部件按其失效特征可分为四类，即轮轴、转向架、车体、钩缓系统、制动系统等关键零部件；车轮踏面、制动闸片、心盘磨耗盘等规律磨耗件；橡胶件、侧架和摇枕等性能衰退件；以及垫片、螺帽、弹簧等批量更换件。对上述零部件进行健康状态监测，建立故障监测指标体系[10]，挖掘关键指标和失效规律的映射关系，从而构建剩余寿命预测模型，是状态修实施的关键要素。车钩作为机车和车辆、车辆和车辆之间连挂和传递纵向作用力的关键部件，因纵向交变载荷引起的疲劳断裂是其常见的失效模式；同时受其他冲击载荷、缺陷和车钩内部接触关系的随机性，探伤的不完备性，以及裂纹尺度的不确定性影响，车钩服役寿命分散性极高，基于解析方法建立用于其剩余寿命预测模型十分困难。在车钩剩余寿命预测方面，目前大多采用仿真方法研究其在某一裂纹条件下的裂纹扩展规律和剩余寿命[11-12]，缺少试验验证；基于台架试验数据得到车钩安全服役里程随可靠度的变化曲线[12-14]，虽能用来预测剩余寿命，但没有与具体运用状态相结合，预测精度有限。

本文提出一种基于假设分布的重载货车关键结构剩余寿命预测方法，在获取结构服役历史中少量退化数据的基础上，可构建合理的结构剩余寿命预测模型。基于该方法，以重载货车车钩为研究对象，将基于线路实测载荷时间序列编制得到的载荷谱作为车钩服役环境，进行疲劳台架试验，基于假设分布对车钩退化数据进行拟合，得到剩余寿命预测图。当有新的车钩裂纹监测数据时，以已服役里程、裂纹位置、裂纹尺寸和可靠度为输入，预测车钩剩余寿命，整体技术路线如图1所示。

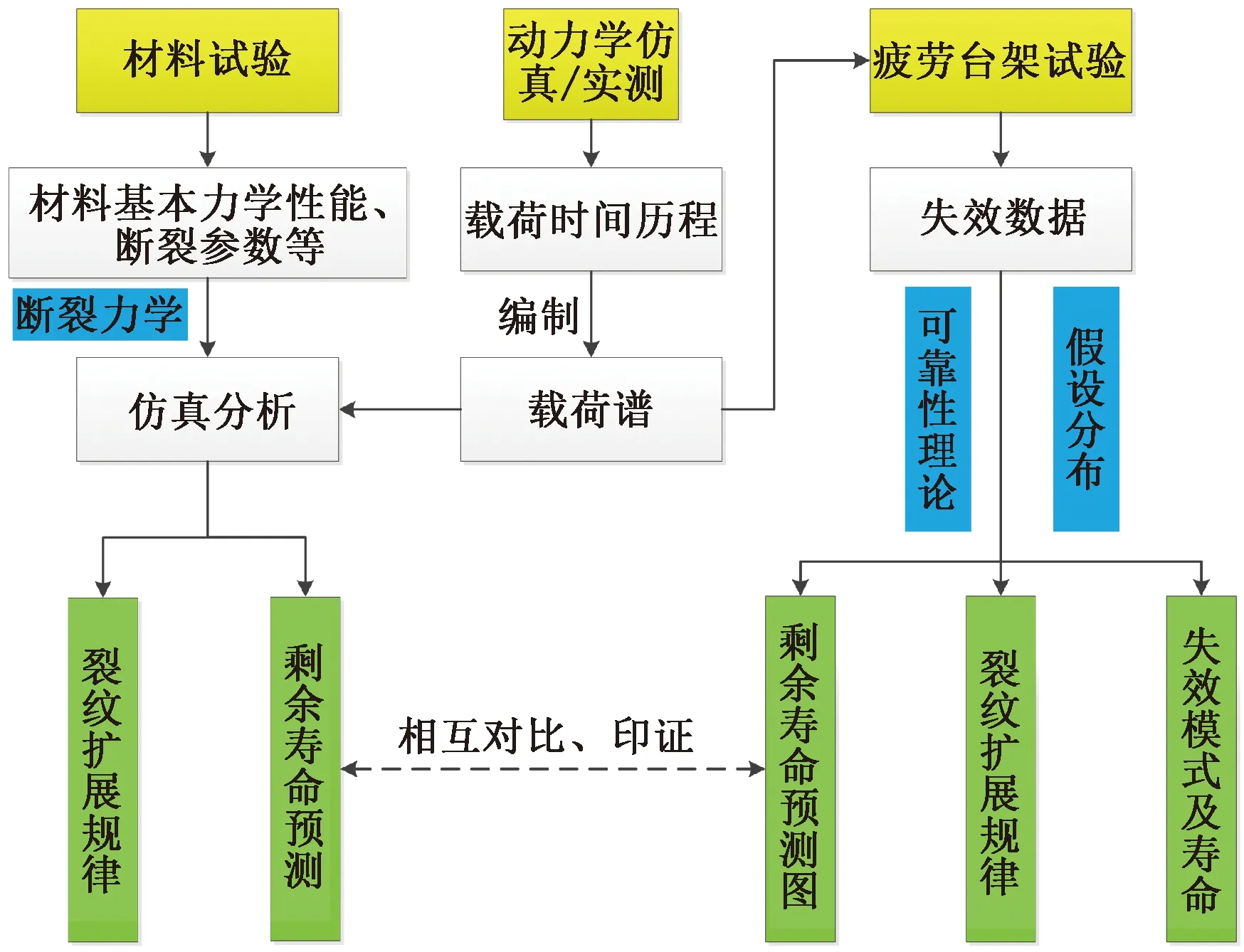
图1 剩余寿命预测整体技术路线

1 可靠性指标与假设分布检验

结构可靠性指结构在规定条件和规定时间下完成预定功能的概率，常用的可靠性指标有可靠度、失效率、平均工作时间等。

若结构服役寿命t的概率密度函数为f(t)，可靠度R(t)定义为服役寿命大于某一规定值t的概率，即

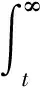
( 1 )

累积失效概率，又称不可靠度，可表示为

F(t)=1-R(t)

( 2 )

计算结构可靠度的关键在于获取结构失效概率密度函数f(t)。对于大样本问题(容量超过50或70)，一般根据数据直接确定概率密度函数；对于小样本问题，可以综合考虑总体拟合效果、疲劳失效机制和算法的安全性，从常用统计分布类型，即三参数Weibull分布(3PWD)、二参数Weibull分布(2PWD)、正态分布(ND)、对数正态分布(LND)、极小值分布(EMVD1)、极大值分布(EMVD2)和指数分布(ED)中选择良好假设分布[15]。基本流程如下：

(1)将数据由小到大排序，基于中位秩计算经验失效概率Pem(xi)

( 3 )

式中：n为数据总数。

(2)基于线性回归，分别用上述常用统计分布类型拟合(xi，Pem(xi))数据，得到各统计分布参量以及拟合相关系数RXY。

(3)对于高可靠度问题，通过计算dF1和dF2来判断尾部预测安全性。

对于左尾部问题，有

dF1=Pem(x1)-Pth(x1)

( 4 )

dF2=Pem(x2)-Pth(x2)

( 5 )

对于右尾部问题，有

dF1=Pem(xn)-Pth(xn)

( 6 )

dF2=Pem(xn-1)-Pth(xn-1)

( 7 )

式中：Pth(xi)为实际失效概率。

综合考虑拟合相关系数、疲劳失效机制和尾部预测安全性，确定良好统计分布类型。

2 载荷谱编制

关键零部件载荷-时间历程的获取可通过线路实测或列车动力学仿真两种途径，当获取载荷时间历程后，可基于以下步骤编制台架试验载荷谱(以车钩纵向载荷为例)。

(1)去除车钩压力，只保留车钩拉力

试验车钩为铸造件，表面粗糙度高，在纵向力的反复作用下容易产生疲劳裂纹，且疲劳裂纹萌生寿命占全寿命的比重较小，几乎可以忽略，只需要考虑车钩裂纹扩展寿命，因此，车钩压力对车钩疲劳寿命几乎没有影响，只需保留拉伸载荷作为车钩疲劳台架试验载荷输入。

(2)对车钩拉伸载荷进行雨流计数

线路实测的车钩载荷时间历程能综合反映重载货车在不同运营工况、线路条件、牵引吨位等多因素影响下的完整车钩载荷信息，但作为随机交变载荷，其特性很难量化，且不宜直接用于结构疲劳试验和可靠性分析，需要采用雨流计数法将随机交变载荷简化为能真实反映车钩受载情况的载荷谱。雨流计数的原则是当交变载荷对应的应力-应变关系构成一个迟滞回线时，就形成一个完整的循环。通过雨流计数法的处理，可以得到每次循环下的载荷均值Fm、幅值Fb以及相应的频次。

(3)等寿命载荷转换

为利于试验，将雨流计数结果转换为脉动载荷，考虑实际台架试验中，车钩力不可能完全卸载到0，因此将载荷的下限统一定为50 kN，采用图2所示等寿命载荷转换图确定每一循环载荷上限Fmax[16]。图2中，Fa为等效载荷幅度，R为应力比。根据文献[17]确定车钩的破坏载荷，因为钩舌的破坏载荷较小，作为车钩破坏载荷相对安全，所以Fb定为3 430 kN。

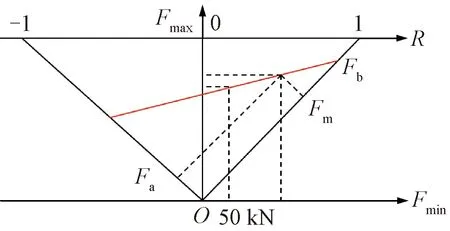
图2 等寿命载荷转换

(4)去除无损载荷

当载荷幅小于某一数值时，结构最大应力幅不大于其疲劳极限，或者含裂纹结构的裂纹前沿应力强度因子幅不大于裂纹扩展阈值，可认为结构不产生损伤。对于铸造车钩来说，裂纹萌生对疲劳寿命影响较小，因此以裂纹前沿应力强度因子幅小于阈值的载荷幅为下限，去除无损载荷。

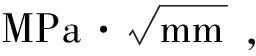
图3 钩舌下牵引凸缘根部安全服役临界裂纹

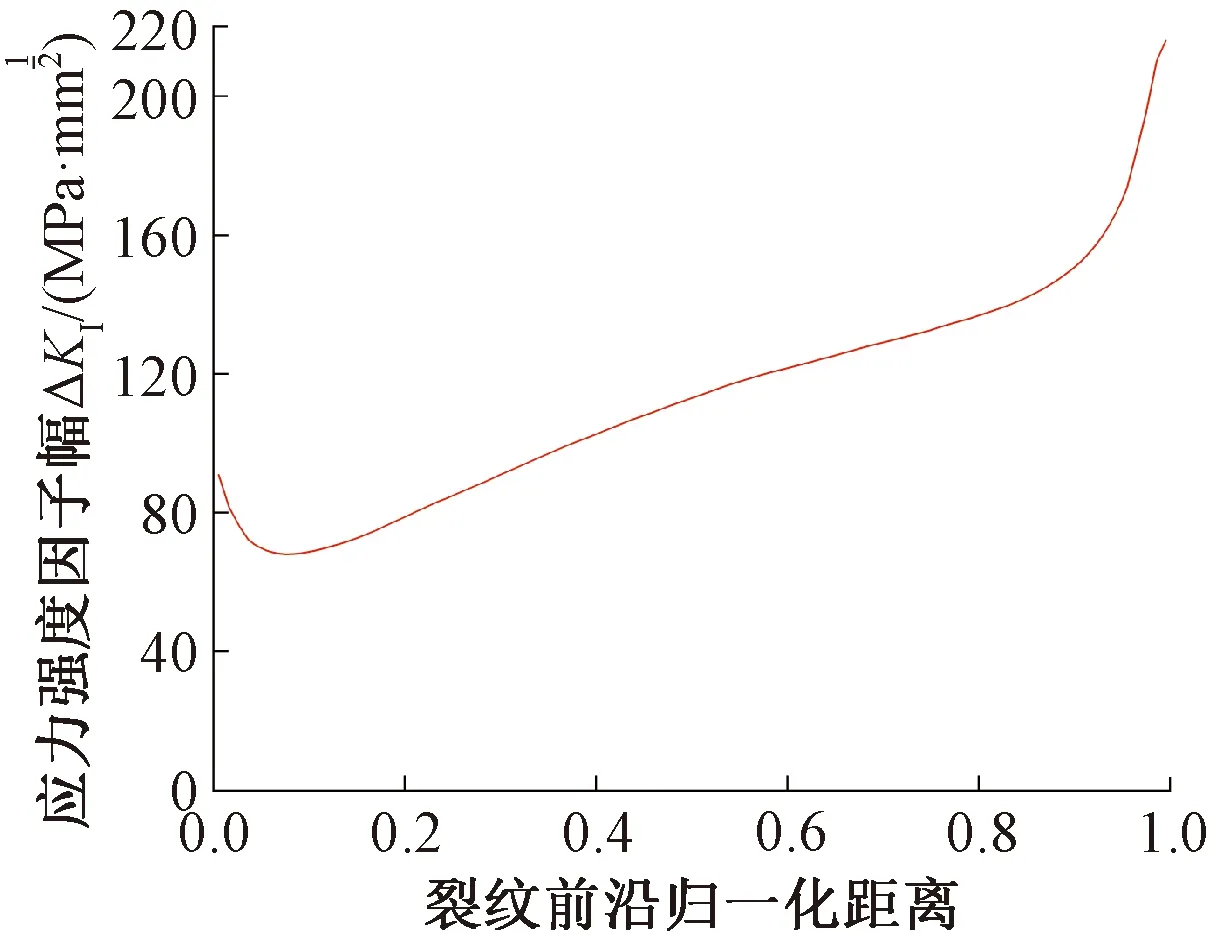
图4 50～185 kN纵向拉力作用下裂纹前沿应力强度因子

(5)载荷分级及损伤当量折算

为方便台架试验施加载荷，可对载荷分级处理成载荷谱，级数越多，载荷谱越接近原始载荷时间历程，但相应会增加台架试验的实施难度和试验周期。当载荷分级完成后，若小载荷频次过多，可基于当量损伤折算[18]将部分小载荷折算至大载荷，以缩短试验周期。

基于以上步骤，最后得到的车钩台架试验载荷谱如图5所示。

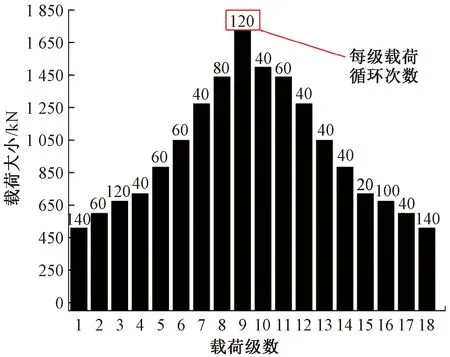
图5 车钩台架试验载荷谱

3 车钩台架试验及数据分析

基于图5车钩台架试验载荷谱，以及车钩疲劳试验台进行完整车钩装配体疲劳台架试验。在试验前，对试件进行荧光探伤，以确保试件没有明显的初始制造缺陷。试验过程中，每3～5个完整载荷循环对车钩进行拆解探伤，同时记录载荷循环次数、裂纹位置和裂纹尺寸。

基于试验结果，车钩裂纹通常出现在钩舌上下牵引凸缘根部、内腕面中部以及钩体下牵引凸缘根部，因钩舌下牵引凸缘、内腕面裂纹和钩体下牵引凸缘裂纹扩展至临界尺寸而失效。

以钩体下牵引凸缘裂纹为例，开展基于假设分布的车钩剩余寿命预测方法研究。通过线性插值计算相同寿命分数下的钩体下牵引凸缘根部裂纹表面长度，见表1。对于样本容量小于等于10的情况，可用Grubbs(格拉布斯)准则法进行异常数据的判断和剔除，经计算，各寿命分数下的异常值见表1标记数据(带*)。裂纹长度均值和变异系数的变化规律如图6所示。

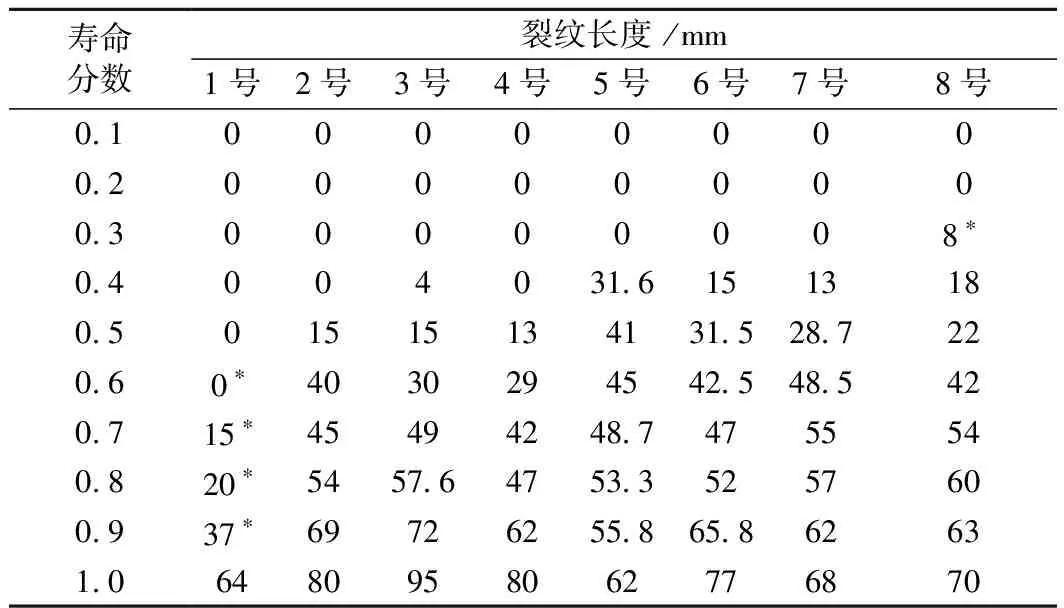
表1 钩体下牵引凸缘裂纹长度随寿命分数演化数据

从图6可以看出，钩体下牵引凸缘裂纹长度均值随着寿命分数的增加而恒增加，而变异系数逐渐减小并趋于稳定，寿命分数大于0.7后，分散性较小。原因是裂纹扩展初期，应力集中部位产生多段小裂纹，小裂纹位置和尺寸的随机性致使分散性较大，在循环载荷的作用下，小裂纹逐渐融合成一条疲劳主裂纹后，裂纹位置相对固定，裂纹尺寸较长且方便测量，此时数据分散性较小。

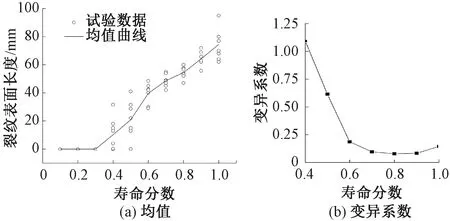
图6 裂纹均值和变异系数随寿命分数的变化

分别采用3PWD、2PWD、ND、LND、EMVD1、EMVD2作为一定寿命分数下裂纹长度的假设分布，并比较各分布函数下的线性相关系数RXY，从而判断假设分布是否合理。表2给出了各假设分布下的拟合相关系数，因寿命分数0.1、0.2、0.3下的裂纹长度数据均为0，表2仅给出其他寿命分数下的裂纹长度数据拟合相关系数。

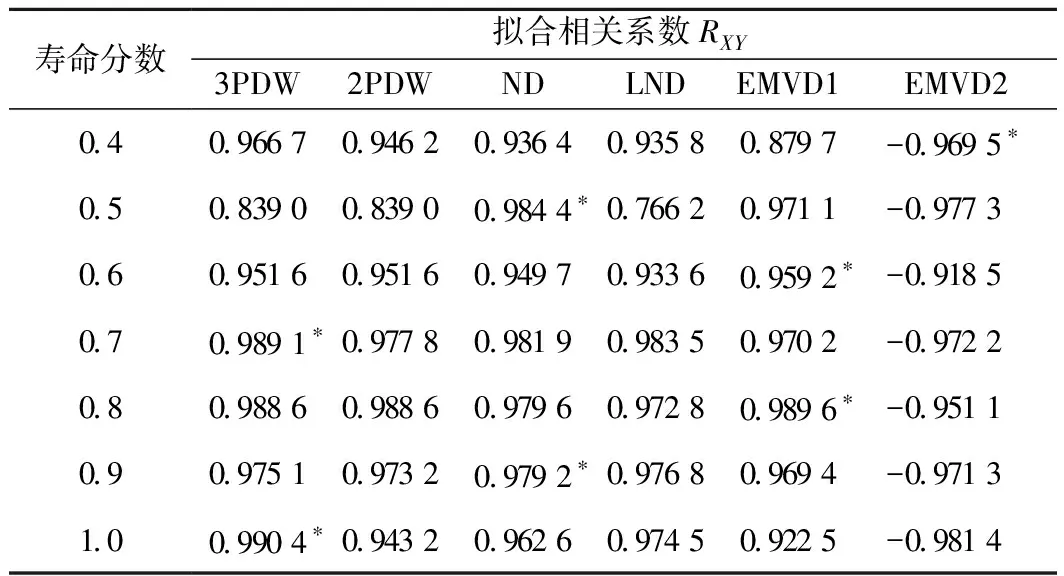
表2 裂纹长度数据在各假设分布下的拟合相关系数

从尾部预测的安全性角度进行分析，表3给出了上述6种假设分布右尾部失效概率经验值与预测值之差(即dF1和dF2)。dF1xn时能给出偏于保守的估计。

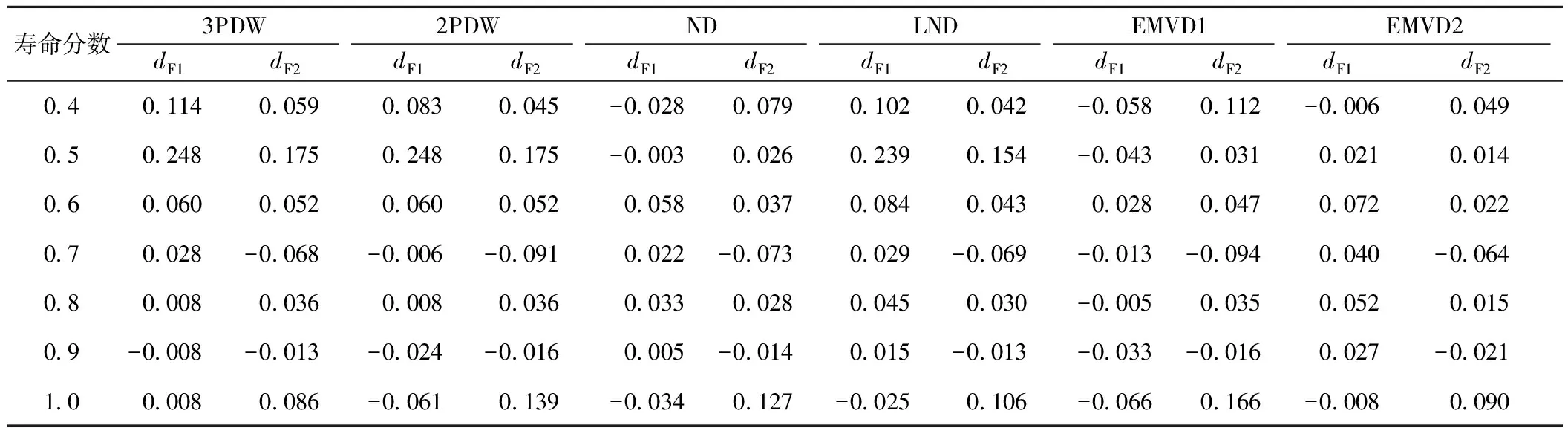
表3 6种假设分布对裂纹长度的右尾部拟合误差

综合考虑拟合程度与尾部预测安全性，EMVD1可作为钩体下牵引凸缘根部裂纹长度数据的良好假设分布。表4给出了不同寿命分数下表面裂纹长度数据的EMVD1累积失效概率函数参量。图7给出了相应的累积失效概率曲线。

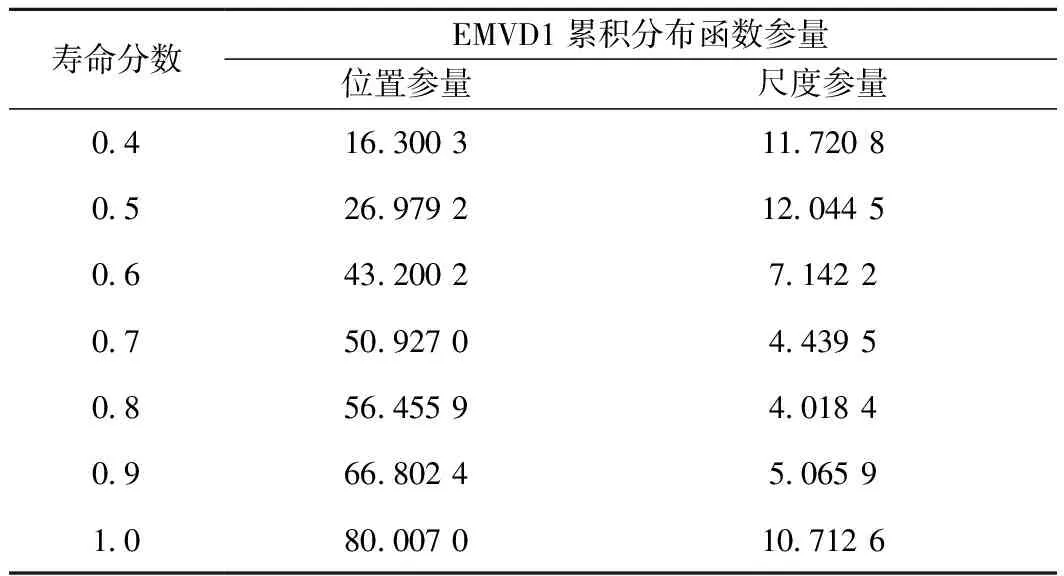
表4 裂纹长度数据的EMVD1累积失效概率函数参量

4 基于断裂力学的结构裂纹扩展分析方法

对于无可用试验退化数据的情况，可在试验获取结构材料断裂力学参数的基础上，通过有限元法，对结构进行裂纹扩展仿真分析，预测一定裂纹尺寸下的结构剩余服役寿命。

4.1 材料基本性能及断裂参数获取

首先，从车钩实物中截取单轴拉伸试样及CT试样，以应变控制或位移控制加载，单调拉伸直至单轴拉伸试样破坏，获得材料应力-应变曲线及基本力学性能。其次，基于文献[19]，使用柔度法，利用COD引伸计测量裂纹长度，首先预制疲劳裂纹，需在小载荷下进行数万至数十万次循环预制疲劳裂纹，保证裂纹尖端的尖锐；利用恒载增K法，测定da/dN>10-5mm/cycle的裂纹扩展速率，用降K法测定裂纹扩展阈值ΔKth，采用Paris公式进行数据拟合，获得裂纹扩展速率参数C、m。基于文献[20]，测定材料裂纹失稳扩展断裂时的断裂韧性KIC。车钩材料(铸造E级钢)具体参数见表5。

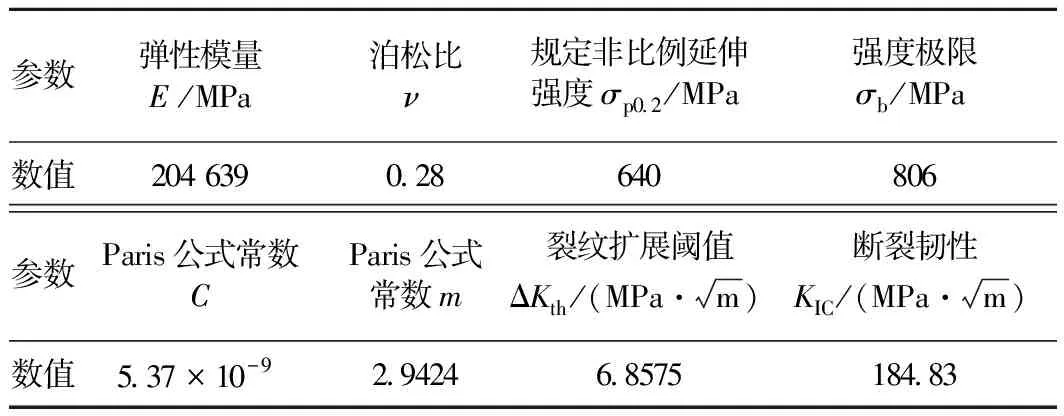
表5 车钩材料(铸造E级钢)基本力学性能及断裂参数

4.2 结构裂纹扩展仿真分析方法

基于获取的材料参数，建立一定边界条件下的结构剩余寿命预测有限元模型，通过对引入缺陷下结构应力分布分析，提取危险部位的应力，进行三维裂纹扩展分析和剩余寿命预测。具体的裂纹扩展分析流程如图8所示。

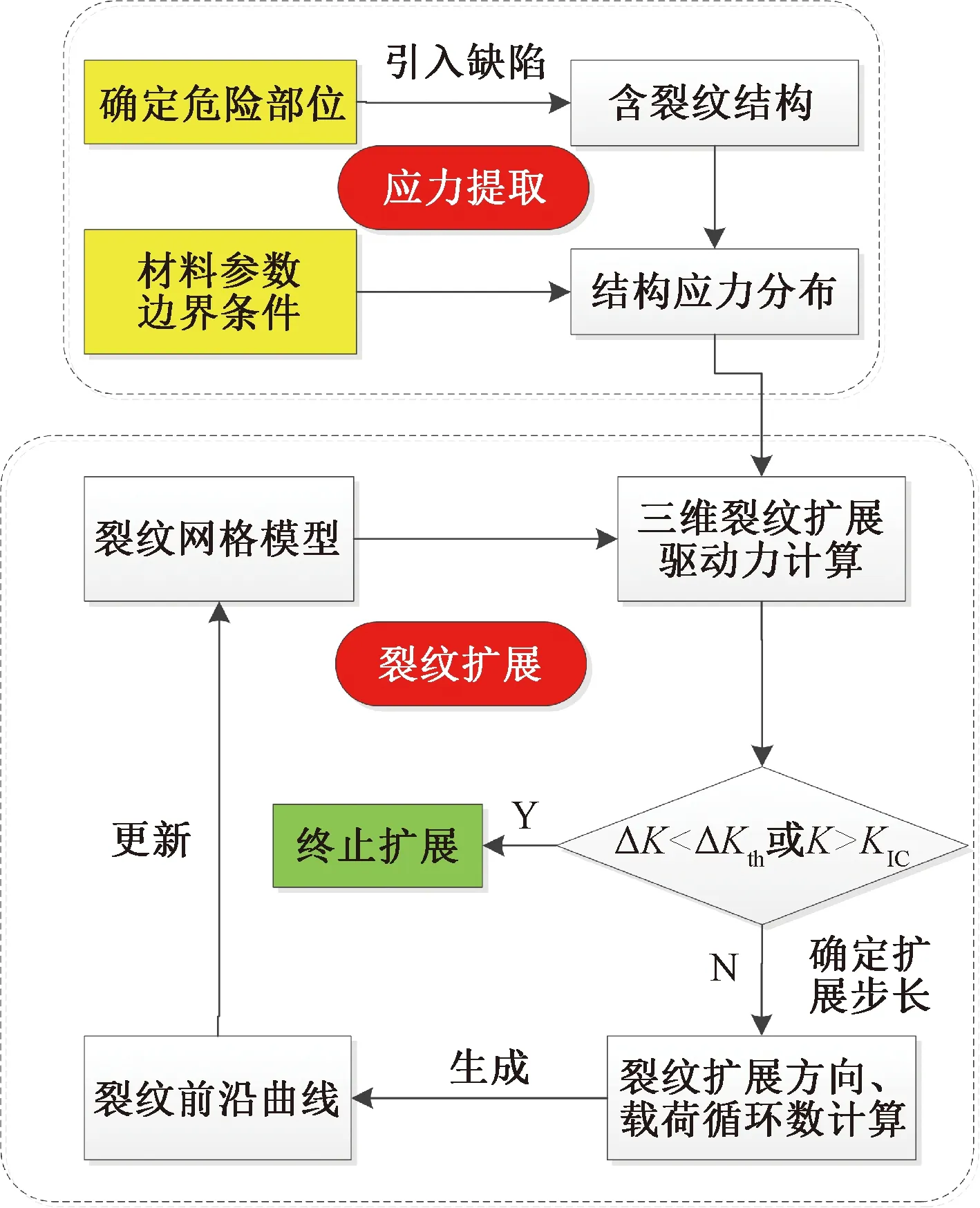
图8 裂纹扩展分析流程

4.3 钩体下牵引凸缘裂纹扩展分析

基于文献[21]研究成果，半车钩有限元计算模型(如图9所示)能较好地模拟车钩在纵向牵引力作用下的真实受力状态。依据半车钩有限元模型建立钩体下牵引凸缘局部子模型，在图5所示载荷谱作用下，对结构在下牵引凸缘根部应力最大处引入长4 mm、深0.8 mm的初始半椭圆表面裂纹，并基于图8所示流程，在通用有限元分析软件的基础上，结合二次开发程序进行钩体裂纹扩展分析，子模型初始裂纹状态和失效临界状态如图10所示，图11给出了计算所得裂纹表面长度随服役里程的变化曲线。

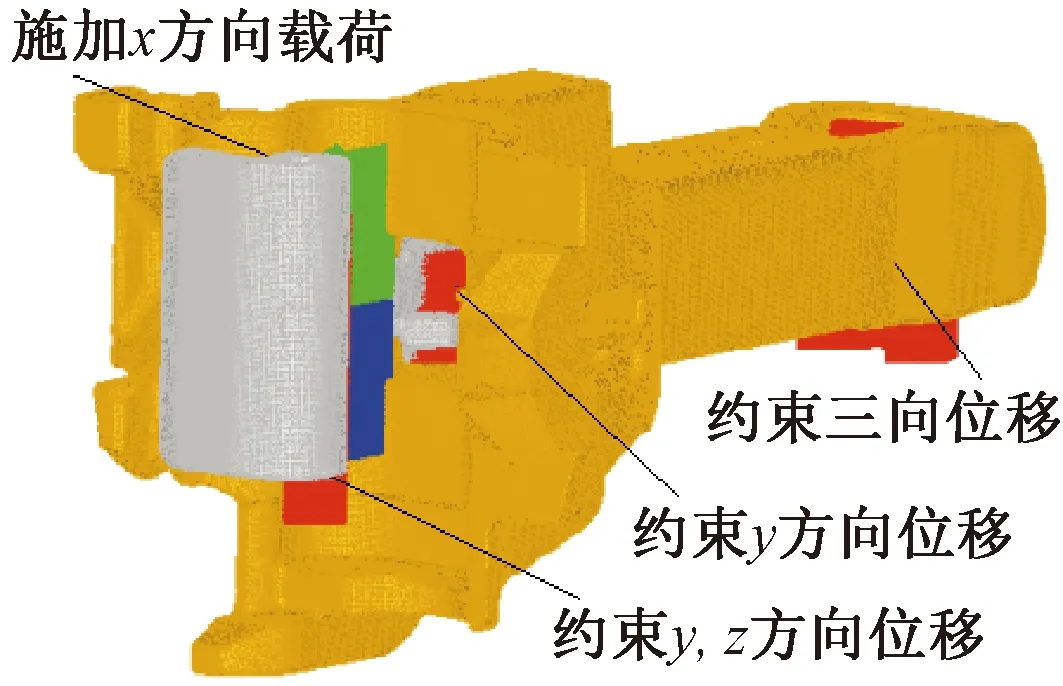
图9 车钩有限元计算模型

图10 钩体下牵引凸缘根部初始裂纹及失效临界状态

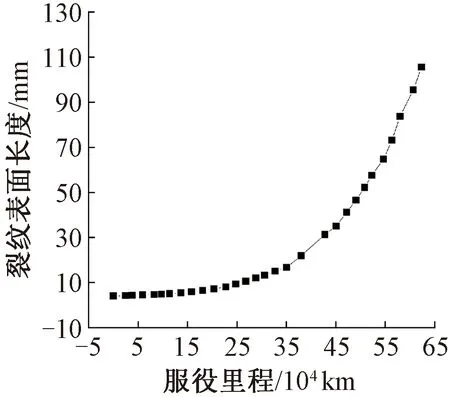
图11 裂纹表面长度随服役里程的变化

5 钩体剩余寿命预测模型

基于图7，给定钩体下牵引凸缘根部裂纹表面长度和可靠度(或累积失效概率)，可进行钩体剩余寿命预测。具体方法如下：假设某钩体已经服役了kkm，通过探伤检测到下牵引凸缘根部裂纹长30 mm(对应图7中横坐标)，当失效概率为0.05时(对应图7中纵坐标)，可在图中作出一个点，这个点落在寿命分数为0.6～0.7的曲线中间，通过线性插值可得到服役寿命约为全寿命的67%，因此全寿命应为1.49kkm，即此钩体的剩余运用里程为0.49kkm，且这一结论具有95%的可靠度。

对于无可用试验数据的情况，可基于图8，在钩体下牵引凸缘根部应力最大处引入初始裂纹，通过基于断裂力学的有限元分析方法，分析钩体结构在图5所示疲劳载荷谱下的剩余服役寿命，结果如图11所示。

图12分别给出了7个钩体基于假设分布的剩余寿面预测结果、基于仿真分析的剩余寿命预测结果与实际剩余寿命的对比。由于钩体材料、工艺制造等方面的分散性，在图5所示载荷谱循环作用下，相同结构的钩体在裂纹位置、数量及尺寸上均具有一定的差异性，从图12可以看出，7个钩体的服役寿命均有所不同，从150万km到300万km不等，此外每个钩体出现可视裂纹所对应的里程也有所不同；基于假设分布的剩余寿命预测均值与实际剩余寿命趋势基本一致，当探伤里程较短时，误差相对较大，随着探伤里程的增大，多段小裂纹融合成主裂纹后，预测精度较高。整体来看，平均相对误差为38.35%，考虑到铸造件本身的分散性较大，以及磁粉探伤精度误差，平均相对误差在工程应用可接受范围之内。基于仿真分析的剩余寿命预测结果相对保守，原因在于仿真分析未考虑车钩结构不同部位多裂纹对车钩系统可靠度的影响[22]。

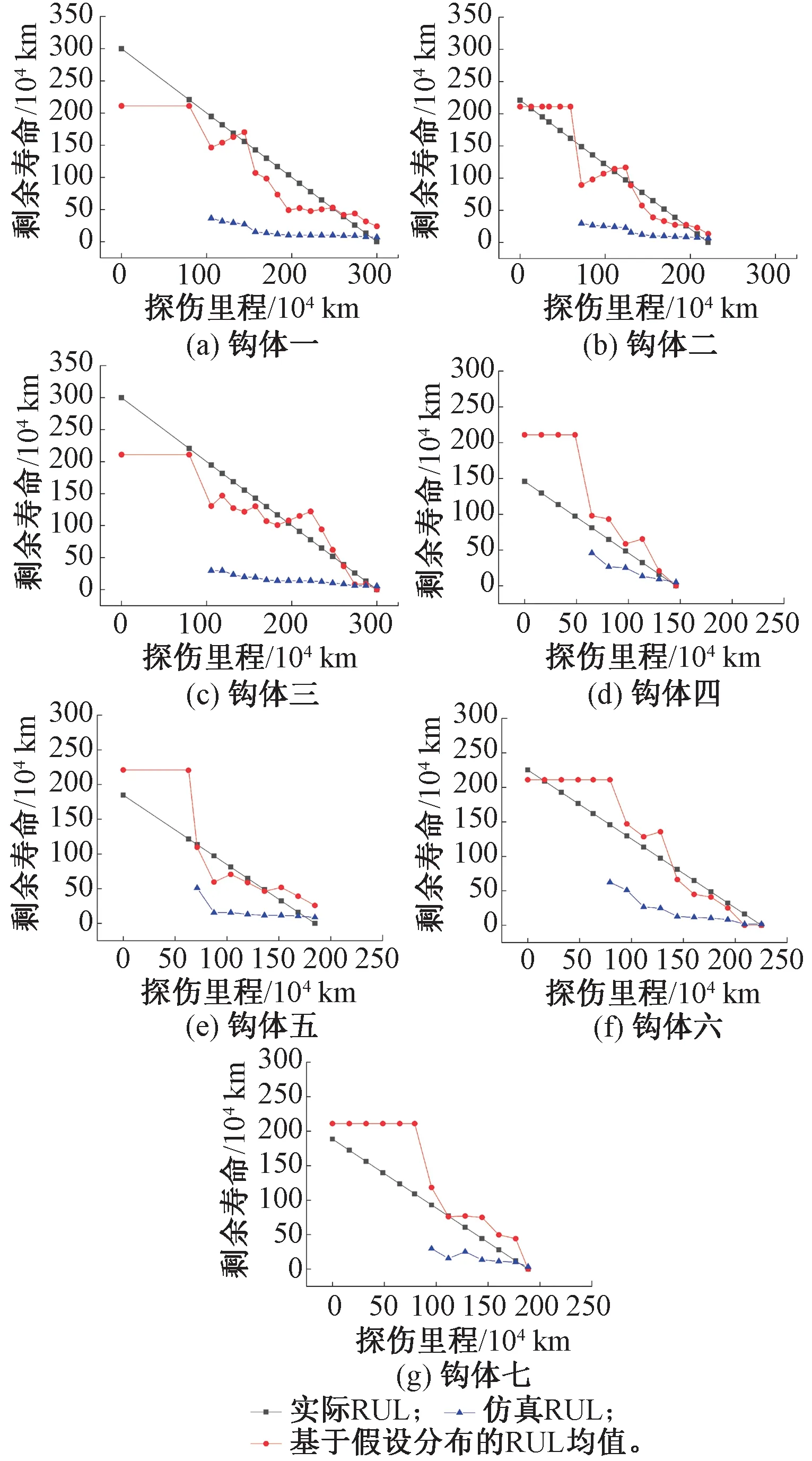
图12 预测剩余寿命与实际剩余寿命对比

6 结论

(1) 提出基于假设分布的重载货车关键结构剩余寿命预测方法，给出完整的寿命预测流程，并以车钩为例，给出了详细的结构载荷获取、载荷谱编制、台架试验、数据分析、累积失效概率曲线绘制、剩余寿命预测等方法要素。

(2) 以重载货车钩体为研究对象，基于假设分布的剩余寿命预测均值与实际剩余寿命趋势基本一致，整体平均相对误差为38.35%，在工程应用可接受范围之内，且相对误差随着探伤里程的增大呈减小趋势。

(3) 对于无可用试验数据的情况，可基于断裂力学理论对车钩进行裂纹扩展仿真分析来预测一定裂纹尺寸下的剩余服役寿命，若结果过于保守，可进一步考虑车钩结构不同部位多裂纹对车钩系统可靠度的影响来提高预测精度。

本文的研究结果对于重载货车关键零部件剩余寿命预测、结构优化设计、货车状态修的实施、经济效益的提高和应用安全性具有重要的理论和工程指导价值。