基于双尺度度量的改进模糊均值曲线聚类方法研究

陈甜甜，高亚静，卢占会*

（1.华北电力大学数理学院，北京 102206；2.中国华能集团碳中和研究所，北京 100031）

0 引言

随着电力网络的智能化发展，数据采集的密集化程度越来越高，电力网络中存在许多随时间变化表现出明显曲线特征的函数型数据［1］，如风电功率曲线、光伏功率曲线、电力负荷曲线等，有效挖掘数据的价值是电力系统运营的关键环节［2］。其中，对函数型数据聚类，即曲线聚类，可以有效挖掘数据信息，在新能源出力特性分析［3］、典型场景提取［4］、电能质量评估［5］、电力负荷曲线聚类［6］等方面具有重要的应用价值。

曲线聚类的研究已经比较深入，常用的聚类算法主要有：K-means、模糊C 均值（Fuzzy C-means，FCM）、密度峰值聚类（Density Peaks Clustering，DPC）、高斯混合模型聚类（Gaussian Mixture Model，GMM）、自组织映射神经网络（Self-Organizing Map，SOM）等。其中模糊C均值聚类算法在运行时间、准确度、稳定性及聚类效果等方面均表现较好，并因其结构简单而广为应用［7］。但模糊C 均值聚类算法存在聚类数目难以确定、初始聚类中心的选取对算法的聚类效果比较敏感、容易陷入局部最优等缺点［8］，因此很多文献对算法进行了改进。一方面，采用搜索式算法对聚类算法进行优化：文献［9］利用模拟退火遗传算法优化FCM 算法初始聚类中心的选取，并采用评价模糊聚类效果的Xie-Beni（XB）指标对聚类数目进行确定，提升了算法的聚类效果；文献［10］利用灰狼算法的全局搜索能力，搜寻较好的初始聚类中心，降低聚类结果陷入局部最优的可能性。但搜索式算法需人工设置的参数较多，算法性能与参数设置有关，且算法收敛速度较慢。另一方面，结合其他聚类算法设计初始聚类中心的选取：文献［11］使用改进K-means 算法确定初始聚类中心，并引入粒度原理确定最佳聚类数；文献［12］利用快速爬山技术，对标准FCM 的初始聚类中心进行改进，实现用电负荷数据的精准聚类；文献［13］采用系统聚类法来确定初始聚类中心。上述改进初始聚类中心的方法均能有效提高聚类算法的稳定性，但这些方法均基于欧氏距离进行设计，而由函数型数据构成的曲线具有维度高、时序性强等特点，欧氏距离只考虑了曲线对应时间点的数值分布特性，很难反映曲线间的形状相似度［14-15］，并且随着聚类数目的增大，很难寻找到曲线形状差异较大的初始聚类中心，使得聚类算法的聚类效果不佳。

为了解决上述问题，本文对FCM 聚类算法进行改进，即对该算法初始聚类中心的确定进行改进，引入皮尔逊距离与动态时间弯曲（Dynamic Time Warping，DTW）距离来度量曲线间的纵向与横向形状相似度，提出一种基于双尺度度量的密度峰值算法来确定初始聚类中心。为进一步提升聚类效果，利用改进熵权法将皮尔逊距离与DTW 距离结合作为FCM 聚类算法中的相似性度量。改进后的聚类算法能在初始聚类中心确定过程中从2个方向考虑曲线之间的形状相似性且人工设置参数较少。由于风电出力具有随机性与不确定性，易受到温度、风速等环境因素的影响且随时间呈现一定的变化规律［16-18］，其对应的实测数据属于电力行业中典型的函数型数据；同时，对风电曲线进行双尺度聚类，可以反映周期内风电出力的形态变化特征，对含风力发电地区电网规划和调度策略的制定具有重要意义［19-20］。因此，以风电实际出力数据进行聚类分析来验证所提算法的正确性和有效性。

1 FCM算法基本理论

FCM 算法流程如图1 所示，总结FCM 算法的基本步骤如下。

图1 FCM聚类算法流程Fig.1 FCM clustering algorithm flowchart

（1）给定聚类数目c、初始化聚类中心V()0、模糊指数值m以及迭代精度ε。

（2）计算样本与聚类中心间的欧氏距离。

（3）根据式（4）确定隶属度矩阵U。

（4）根据式（5）修正聚类中心。

上述聚类过程中，样本聚类数目c、初始聚类中心V()0需利用先验知识进行确定，成为应用FCM 聚类算法的关键。

2 FCM算法的改进策略

针对电力行业中由函数型数据构成的曲线聚类问题，本文利用FCM 聚类算法对其进行聚类，并针对算法的初始聚类中心选取进行改进，引入皮尔逊距离与动态时间弯曲距离来衡量曲线间的形状相似度，结合密度峰值聚类算法确定初始聚类中心，并在此基础上将皮尔逊距离与DTW 距离融合起来，构建FCM算法新的相似性度量。

2.1 皮尔逊距离

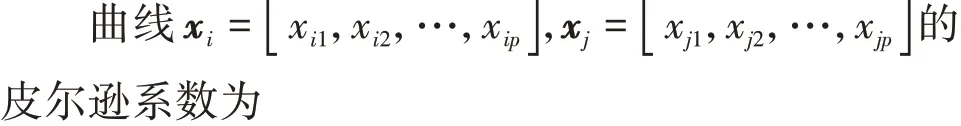
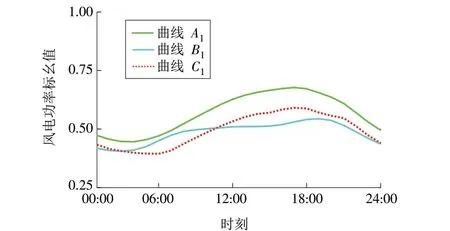
图2 日时序曲线（用皮尔逊距离衡量）Fig.2 Daily time series curve（measured by Pearson distance）

2.2 动态时间弯曲距离

时 间 序 列xi和xj的DTW 距 离dDTW(xi，xj) =L(p1，p2)。

相比于欧氏距离与皮尔逊距离，DTW 距离显示出不同于这2 种距离的优势。如图3 所示，讨论日时序曲线C2关于日时序曲线A2和B2的相似度，采用 欧 氏 距 离 衡 量 得，deu(A2，C2) = 0.139 2，deu(B2，C2) = 0.112 6，采用皮尔逊距离衡量可得dPearson(A2，C2) = 0.196 8，dPearson(B2，C2) = 0.094 3，均表明曲线C2与曲线B2更接近。但事实上，日时序曲线C2的变化趋势与曲线A2更一致，形状更接近。此时若采用欧氏距离与皮尔逊距离进行相似度衡量则容易出现误差，导致聚类结果产生偏差。而采用DTW 距离衡量日时序曲线的相似度，则可以得到dDTW(A2，C2) = 0.352 9，dDTW(B2，C2) = 0.361 5，表 明曲线C2与曲线A2更接近。

图3 日时序曲线（用动态时间弯曲距离衡量）Fig.3 Daily time series curve（measured by dynamic time warping distance）

由2.1 节可知，皮尔逊距离可以在一定程度上衡量2 条曲线间的形状相似度，通过分析皮尔逊距离公式可知，将曲线xi移动到axi+b，曲线xj移动到cxj+d（其中a，b，c，d为常数）后，皮尔逊距离的值不发生改变。因此，根据皮尔逊距离显示出的平移不变性，皮尔逊距离可以更好地描述曲线间的纵向形状相似性。而在2 条曲线幅值接近的情况下，DTW距离可以有效衡量2条曲线间的横向形状相似性。

2.3 基于2种度量的初始聚类中心选取

标准FCM 算法需要人工选取初始聚类中心，初始聚类中心不同，聚类结果会相差甚远。若从原始样本中随机选取初始聚类中心，聚类结果不稳定且容易陷入局部最优。为寻找合适的初始聚类中心，本文借鉴密度峰值聚类算法的思想［24］，并且根据函数型数据构成的曲线特性，用DTW 距离作为描述曲线间横向相似度的指标，用皮尔逊距离作为描述曲线间纵向形状相似度的指标，寻找局部密度高且与高密度样本间距离较远的样本作为初始聚类中心。

2.4 FCM算法中的相似性度量

由2.1，2.2 节可知，皮尔逊距离可以描述2 条曲线间纵向形状相似度，DTW 距离可以有效度量2条曲线间的横向形状相似度。因此，本文综合采用皮尔逊距离与DTW 距离，提出一种兼顾曲线纵向与横向形状的相似度衡量方法。

式中：dDTW，max与dPearson，max分别为数据集内所有曲线DTW距离与皮尔逊距离的最大值；dDTW，min与dPearson，min分别为数据集内所有曲线2种距离的最小值。

根据皮尔逊距离与DTW 距离的特性可知，综合距离D(xi，xj)的值越小，2条曲线的相似度越高。为了更加准确地利用综合距离衡量2条曲线间的相似程度，本文采用改进熵权法来确定式（10）中2 种相似度指标的权重［26］。该方法是根据各指标的熵值大小来衡量指标间的差异，由此确定各指标的权重，即相似度衡量指标的值相差越大，则其对应的熵值就越小，该指标包含的有效信息越多，对应的权重越大。具体计算步骤如下。

（1）计算熵值hg。在有G个指标、T个被评价对象的问题中，第g个指标的熵值由式（12）—（14）决定。

显然，对于所有曲线样本，被评价对象为2个样本间的距离，评价指标为通过比例系数调整后的皮尔逊距离与DTW距离。

2.5 改进FCM算法流程

改进FCM 算法流程如图4 所示，具体算法步骤如下。

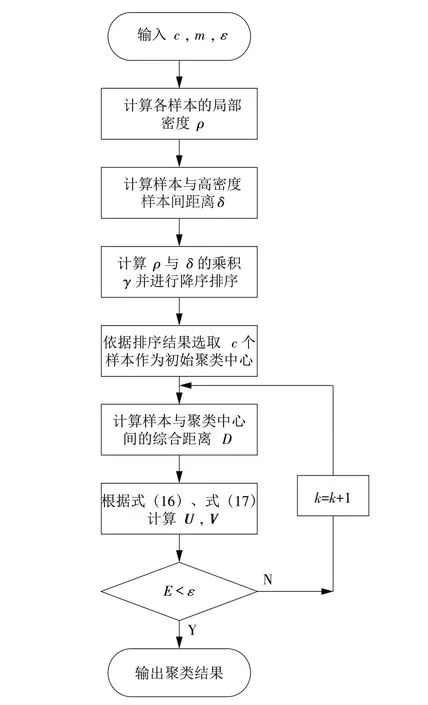
图4 改进FCM聚类算法流程Fig.4 Improved FCM clustering algorithm flowchart

（1）输入聚类数目c、模糊指数值m以及迭代精度ε。

式中：1 ≤i≤n，1 ≤j≤c。

根据式（16）、式（17）更新隶属度矩阵V与聚类中心矩阵U。

3 聚类有效性评价指标

聚类的有效性一般通过聚类评价指标来评价，如误差平方和、XB 指标、Davies-Bouldin Index（DBI）指标、Calinski-Harabasz Index（CHI）指标等。本文选取基于综合距离的XB 指标来确定最优聚类数［27］，并从评价曲线形状相似度的角度出发，构建指标SI来辅助评价曲线聚类效果。

3.1 最优聚类数的确定

聚类的有效性主要通过类间距离和类内距离来衡量。XB 指标综合考虑了类间的分离度S1和类内的紧密度M1。采用XB 指标来确定聚类过程中的最优聚类数。

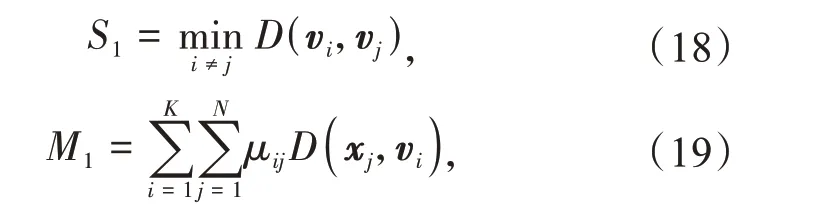
式中：K为聚类数；vi为第i类的聚类中心；xj为样本；N为样本数；μij为样本xj属于第i类的隶属度；D(·)为综合距离函数。

3.2 曲线形状相似度指标

以簇内所有曲线与该簇聚类中心的综合距离平均值S2作为该簇曲线形状相似度指标，其值越小，表明簇内曲线相似度越高。

ISI仅从类内的紧密度角度进行评价，随着聚类数的增大，该指标值不断减小，因此，无法精确确定聚类算法的聚类数。但作为一种辅助聚类效果评价指标，当聚类数目确定时，不同算法的SI 指标越小，则类内曲线越相似，即聚类效果越好。

4 算例分析

本文以美国西部地区2020 年366 条日风电出力曲线为试验数据集进行算例分析。由于风电出力通常具有明显的季节分布特性，因此，首先选取该地区春季风电出力数据进行聚类分析来验证算法的有效性，然后对该地区其余季节风电出力数据进行聚类。

4.1 基于2种算法的春季风电出力曲线聚类

在对曲线进行聚类前，首先对每条曲线采取除以该曲线中元素最大值的归一化处理方法，该方法可将数据映射到(0，1]范围内而不改变曲线形状且能减少算法的迭代次数，然后采用标准FCM 算法与改进FCM算法对77条春季风电出力曲线进行聚类。

4.1.1 最优聚类数的确定

由于FCM 聚类算法需人工确定聚类数目，而聚类数c的取值范围为2至总样本数，为缩小最大聚类数的取值范围，本文采用近邻传播(Affinity Propagation，AP）聚类算法来确定最大聚类数为10［28］，此时，聚类数c的取值范围为[2，10]。为确定最优聚类数，在取值范围内设置不同的聚类数依次进行聚类并记录XB 指标的值。采用标准的FCM 算法进行对比，对比了聚类数K的取值为2～10 的情形，试验各进行30 次，对于每个聚类数，取对应的XB 指标最小值作为该算法在聚类数下的最优聚类结果，试验结果如图5所示。

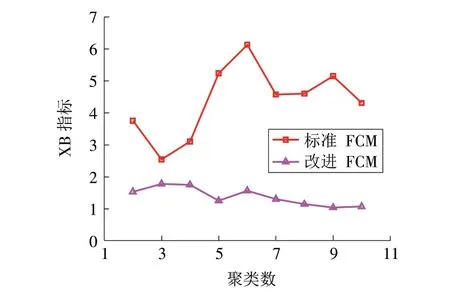
图5 基于XB指标确定最优聚类数Fig.5 The best clustering number based on XB index

由图5 可知，改进FCM 算法的XB 值均小于标准FCM 聚类算法，且当聚类数为5 时，改进FCM 算法对应的XB 值第1次达到最小，因此本文将聚类数定为5。

4.1.2 2种算法聚类结果及聚类效果评价

采用2 种方法分别对77 条日风电出力曲线进行聚类和作图，结果对比如图6所示。

观察图6 可以发现，标准FCM 算法得到的第1、第2 类曲线簇中包含明显不属于该类的曲线，存在曲线错分的情况。进一步对比2种算法的簇内曲线形状相似度S2以及2 类算法的聚类评价指标，结果见表1、表2。

由表1 可见，改进算法的前4 类S2均小于标准算法，第5 类指标值稍大一些。但综合图6、表2 中XB，SI指标值看，改进FCM算法聚类效果更佳。

表1 2种算法簇内形状相似度对比Table 1 Comparison of the shape similarity in clusters of the two algorithms

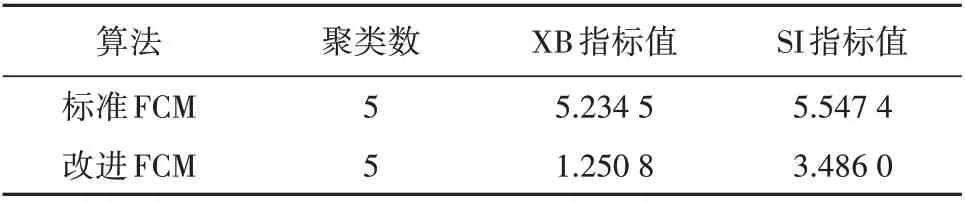
表2 2种算法聚类评价指标对比Table 2 Comparison of the clustering evaluation indexes of the two algorithms

图6 2种算法聚类结果对比Fig.6 Comparison of the clustering effects of the two algorithms

提取2 种算法聚类得到的聚类中心如图7 所示。观察图7a，标准FCM 算法得到的各聚类中心曲线仅在幅值上有区别，尤其是第1 类与第3 类中心曲线的形态几乎一致，在实际中应分为一类。而观察图7b，改进FCM 算法得到的聚类中心曲线在注重曲线幅值大小的同时，曲线形态上也有所区别，对比第1类与第3类曲线，第1类曲线呈缓慢下降再上升的趋势，而第3 类曲线呈现出先上升后下降的趋势，应分为2类。因此，采用改进FCM算法聚类可以对曲线类别有较为精细的划分。

图7 2种算法的聚类中心对比Fig.7 Comparison of clustering centers of two different algorithms

由于算法的稳定性也是衡量算法性能的重要指标，因此本文根据各聚类数下30 次试验中XB 指标达到最小值的次数来衡量算法的稳定性。对比改进FCM 和标准FCM 算法在聚类数为5～10 情形下的10次XB指标，如图8所示。

从图8 可以看出：标准FCM 算法在各聚类数下XB 指标结果相差大，稳定性较差；而改进FCM 算法聚类结果基本一致，具有较高的稳定性。

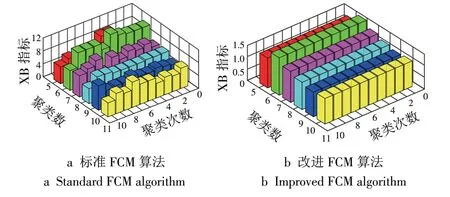
图8 不同聚类数下2种算法的XB指标Fig.8 XB indexes of two different algorithms with different clustering numbers

4.2 改进FCM算法性能分析

为更深入地研究文本提出的改进FCM 算法在初始聚类中心选取以及相似度度量方面的综合性能，采用春季风电出力数据，从仅改进初始聚类中心与仅改进相似度度量2个方面选取几种方法进行对比分析。

4.2.1 初始聚类中心选取对算法的影响

为验证算法在初始聚类中心选取方面进行改进的必要性，在相似度度量均选取综合距离的基础上，对比分析改进K-means 法（文献［11］所述方法）、欧氏密度峰值及本文方法，各改进聚类算法的性能指标见表3。

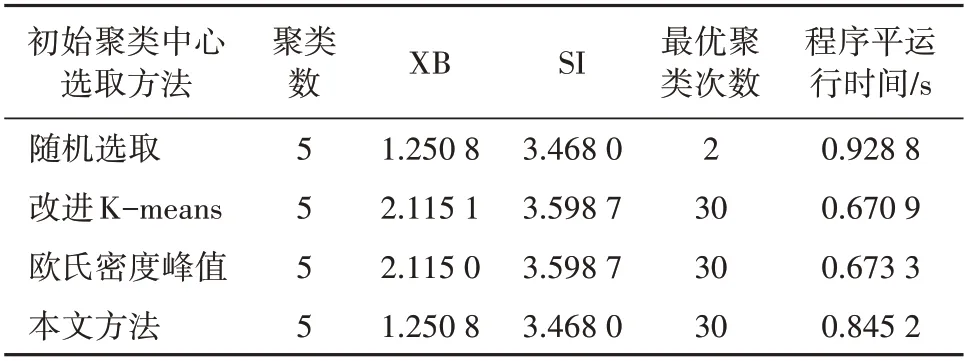
表3 初始聚类中心选取方法对比Table 3 Comparison of the selection method for initial cluster center

由表3 可知，在各程序平均运行时间相差不超过0.3 s 的情况下，相较于随机选取方法，采用各种初始聚类中心选取方法选取初始聚类中心得到的聚类结果稳定性较优，这表明FCM 算法的稳定性是由初始聚类中心的选取所决定的。但通过表3还可以看出，其他2 种初始聚类中心选取方法得到的XB值与SI 值均大于本文方法，进一步对比3 种方法在各聚类数下的XB指标（如图9所示），随着聚类数的增大，改进K-means 法与欧氏密度峰值法的XB 值与本文方法相差较大，容易得到局部最优结果。

图9 初始聚类中心选取对聚类效果的影响Fig.9 Influence of the initial clustering center selection on clustering effect

4.2.2 相似度度量对算法的影响

在曲线聚类过程中，相似度度量的选取是重要的一部分，为消除初始聚类中心选取对算法的影响，这里在确定初始聚类中心的基础上，采用欧氏距离、皮尔逊距离、DTW 距离以及综合距离（本文方法）作为算法的相似度度量。通过反复试验和研究，得到各改进聚类算法确定的最优聚类数与XB指标，见表4。

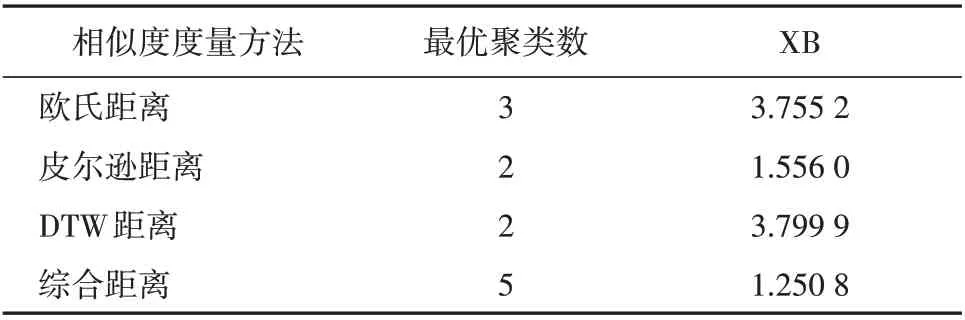
表4 各相似度度量方法XB指标对比Table 4 Comparison of XB index of different similarity measurement methods

通过表4 可以看出，相似度度量不同导致算法的最优聚类数不同。相较于其他距离，使用综合距离作为算法的相似度度量的XB 指标值最小，划分的聚类数较细，得到的聚类结果较优。进一步对比聚类数为5 时各相似度度量方法的性能指标，见表5。

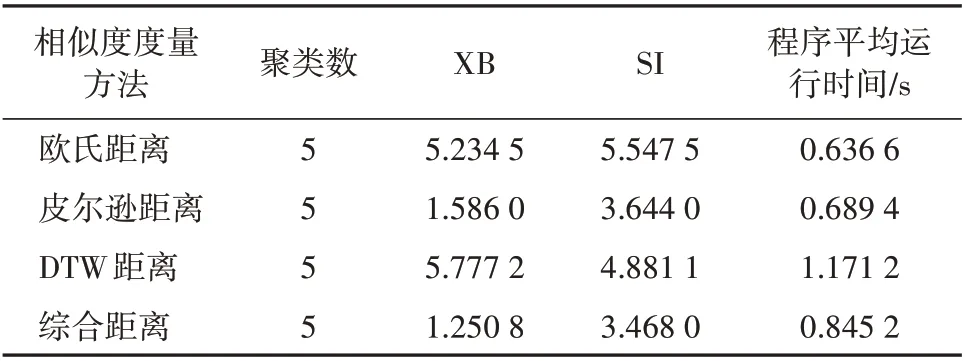
表5 聚类数为5时各相似度度量方法性能指标对比Table 5 Performance indicators of similarity measurement methods with a clustering number of five

通过表5 可以看出，在聚类数均为5 的情况下，相较于欧氏距离与皮尔逊距离，利用综合距离作为相似度度量方法的运行时间有所增加，这是由于DTW 距离的计算复杂度高。但采用综合距离作为相似度度量方法得到的XB，SI 值最小，在各程序运行时间相差较小的情况下，聚类效果大幅提升。

由于综合距离中的权重指标也是影响算法性能的指标，为验证改进熵权法确定的权重指标较优（调整皮尔逊距离权重值为0.495 1，DTW 距离权重值为0.504 9），对综合距离的权重指标选取进行对比，见表6。

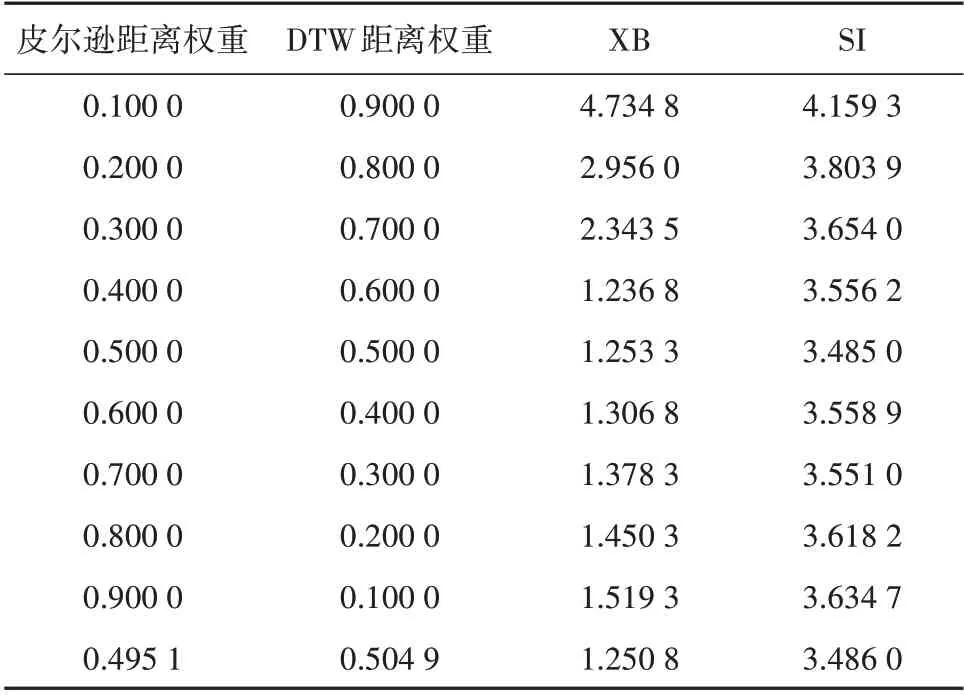
表6 综合距离权重选取对比Table 6 Comprehensive distance weight selection comparison

从表6 可以发现，利用改进熵权法确定权重可以减小权重参数对聚类算法效果的干扰，在得到较优的聚类效果的同时，减少了参数设置带来的试验次数。

4.3 其余季节风电出力聚类结果

利用本文所提算法对该地区其余季节风电出力数据进行聚类，所得结果如图10—12所示。提取春夏秋冬季节聚类中心作为该地区风电出力典型场景，如图13所示。

图10 夏季风电出力聚类结果Fig.10 Clustering results of wind power output in summer

由图10—13 可以看出，该地区春、夏、秋、冬季风电出力分别有5，3，4，5 种典型场景，不同季节下的典型场景曲线形态差异明显，具有明显的季节分布特性。图10 表明，该地区夏季风力较小，风电出力整体变化平缓，昼夜风电出力波动不明显；而图12 中第2 类、第4 类典型场景表明该地区冬季昼夜风电出力波动性大、峰谷明显，呈现出明显的反调峰特性。

图11 秋季风电出力聚类结果Fig.11 Clustering results of wind power output in autumn

图12 冬季风电出力聚类结果Fig.12 Clustering results of wind power output in winter

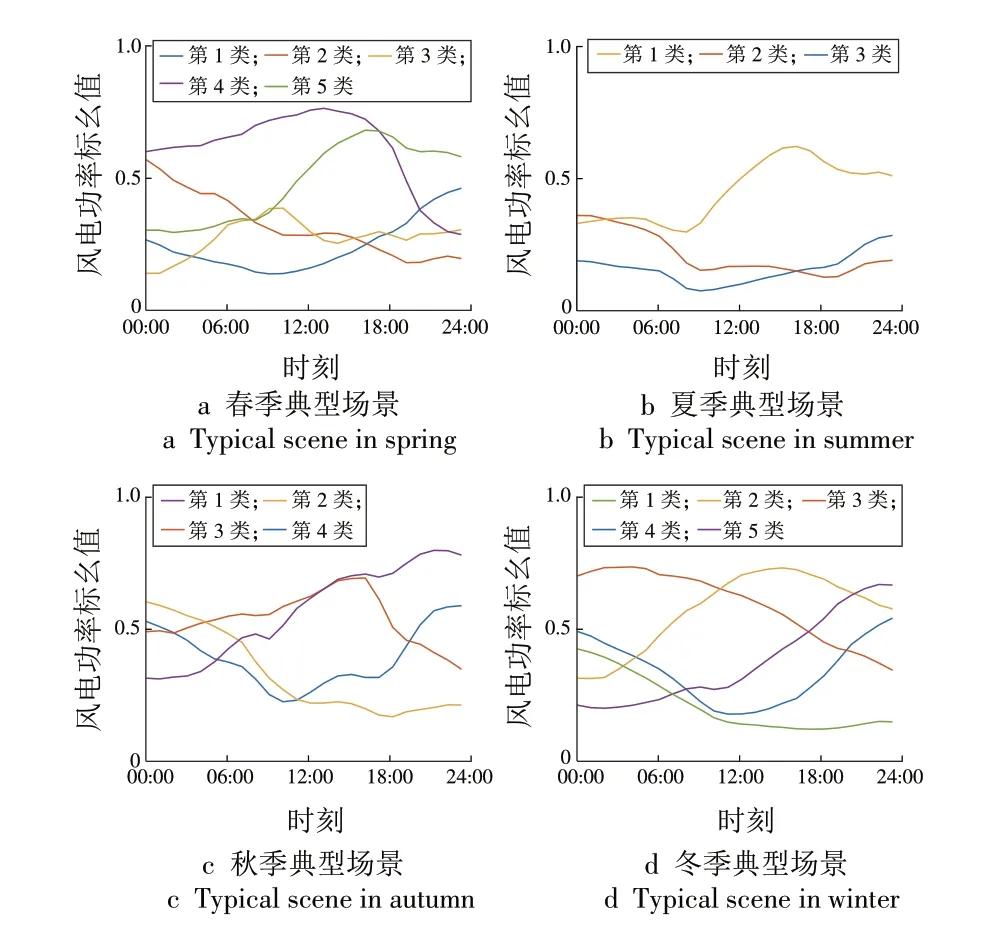
图13 春夏秋冬风电出力典型场景Fig.13 Typical wind power output curves in different seasons

由此可见，在分类结果较为准确的情况下，本文所提聚类算法在地区风电出力场景选取方面也具有一定的实用性与科学性。

5 结论

本文针对函数型数据构成的曲线聚类问题，对FCM 算法提出了基于双尺度度量的密度峰值初始聚类中心选取方法和基于改进熵权法的综合相似性度量方法，通过算例验证可得出以下结论。

（1）本文提出的初始聚类中心选取方法可以很好地提升FCM 算法的稳定性，并且与一般以欧氏距离为基础的选取方法相比，聚类效果更好，不容易陷入局部最优。

（2）本文所提的基于改进熵权法的综合相似度度量方法兼顾日负荷曲线的纵向形状相似性与横向形状相似性，可以有效避免聚类过程中曲线的误分，具有良好的聚类效果。

（3）改进FCM 聚类算法可以从曲线形态方面区分各类曲线且得到较为精细的曲线划分结果。