控制器参数对AGC调节性能的影响

曹子飞，杨栋，吴茂坤，王友龙，潘凤萍，吴振龙

（1.华电莱州发电有限公司，山东烟台 261441；2.南方电网电力科技股份有限公司，广州 510080；3.郑州大学电气工程学院，郑州 450001）

0 引言

“双碳”目标下构建新型电力系统，会有风能、光伏等新能源大规模并入电网，燃煤机组需要通过快速响应的自动发电控制（Automatic Generation Control，AGC）指令来吸纳大规模新能源［1］。为了衡量机组AGC 响应过程中的性能，目前国内采用AGC调节性能指标对参与AGC的机组进行考核［2］。AGC调节性能指标主要包括调节速率、调节精度和响应时间，三者均有明确的定义和计算方法。

许多学者已对优化AGC 运行进行了研究：文献［3］通过分析AGC 控制中的常规问题，得到影响控制的关键因素，并对控制回路进行优化；文献［4］考虑通过高压供热机组汽机主控、锅炉主控和燃料主控的控制优化，提升AGC 调节性能；文献［5］建立AGC 分析模型并提出高比例水电系统的AGC 频率偏差系数整定流程，应用验证了该方法的有效性。此外，文献［6］对AGC 调节运行中安全措施、指令核对、参数设置等方面可能面临的问题都进行了讨论。

比例-积分（Proportional-Integral，PI）控制器在燃煤机组的控制中占据着主导地位，并在未来一段时间内保持主导地位［7-8］。分析不同PI 控制器参数对AGC 调节性能影响，对理论上优化控制器参数具有重要的意义。本文通过单一变量法分析控制器参数对于AGC 调节性能的影响，总结参数优化的方法。

协调控制系统（Coordinated Control System，CCS）是燃煤机组参与AGC调节的重要控制回路，基于直接能量平衡（Direct Energy Balance，DEB）的CCS 是应用最广泛的控制结构［9］。结合工程实际，本文研究了DEB 结构下控制器参数对AGC 调节性能的影响。首先介绍AGC 调节性能指标的计算方法，并分析各自的特点；然后介绍了基于DEB 结构的CCS，并对CCS 的控制难点（如强非线性、强耦合等）进行分析；通过单一变量法分析DEB中6个控制器参数对AGC调节性能的影响，并总结优化AGC调节性能时的参数优化方向；最后对本文工作进行总结和展望。

1 AGC调节性能计算方法

AGC 调节性能指标主要包括调节速率、调节精度和响应时间3个指标［2］。

1.1 调节速率

调节速率是指机组响应AGC 指令的速率，一般分为上升速率和下降速率。

煤粉炉在升降负荷的过程中会出现跨启停磨点的过程：若计算机组响应AGC 指令时跨启停磨点，调节速率的计算需要消除启停磨的影响，反之则不需要考虑。综上可知，实际调节速率的计算如下

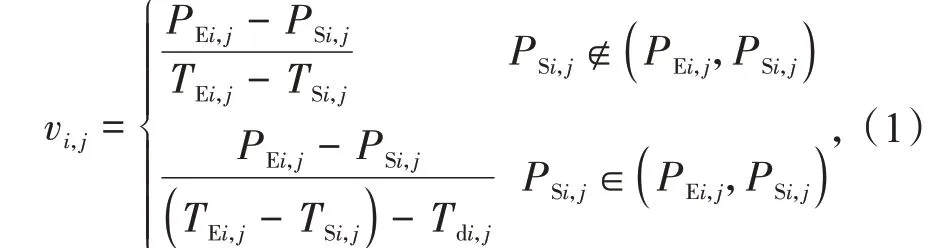
式中：vi，j是第i台机组第j次响应AGC 指令的调节速率，MW/min；PEi，j和PSi，j分别为i机组结束和开始响应时的功率，MW；TEi，j和TSi，j分别为机组响应AGC结束和开始的时刻，min；Tdi，j是第j次响应过程中启停磨实际消耗的时间，min。

基于式（1）可以得到调节速率指标

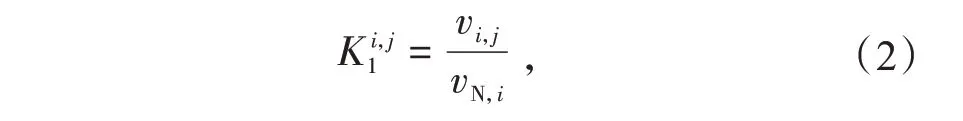
式中：vN，i为不同机组的标准调节速率，MW/min。不同类型机组vN，i单位时间（1 min）调节量占额定有功功率（Pe）的百分比不同，见表1。一般情况下，K i，j1实行最高限制，即K i，j1≤1.2。

表1 不同类型机组的标准调节速率Table 1 Standard regulation rate of different types of units

1.2 调节精度

调节精度指机组在稳定运行过程中，实际出力和功率设定值之间的差值。

在机组平稳运行过程中，对实际出力和功率设定值的差值进行积分，然后得到的积分除以积分时间，可以得到该稳定过程中的调节偏差量，即

1.3 响应时间

响应时间，是指能量管理系统（Energy Management System，EMS）发出指令后，机组在原出力点的基础上可靠地跨出与调节方向一致的调节死区所用的时间。

第i台机组第j次响应AGC指令的响应时间

2 基于直接能量平衡的协调控制系统

2.1 CCS模型状态变量

CCS 是机组参与AGC 调节的核心系统，具有强非线、强耦合等控制特点［10］。以某300 MW 直吹式制粉系统汽包炉机组的非线性CCS 模型为例进行分析。该模型是基于能量守恒和物料守恒并通过必要的简化建立，通过6 个微分方程描述CCS动态［11］

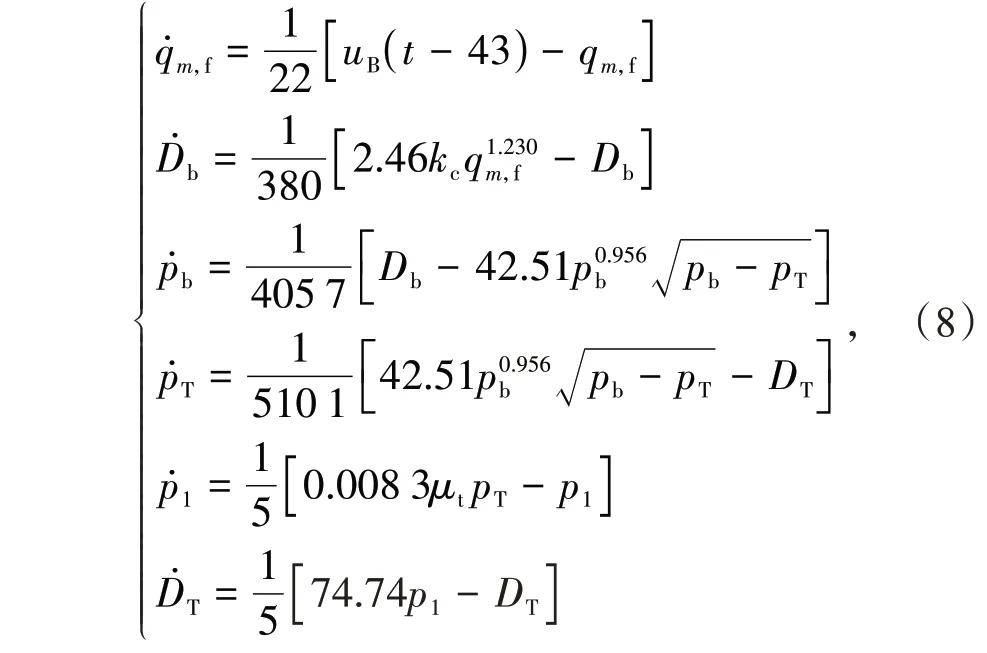
式中：qm，f，Db，DT分别为煤粉质量流量、汽包蒸汽蒸发量、汽机通汽流量，t/h；pb，pT，p1分别为汽包压力、主蒸汽压力、调节级压力，MPa；uB为给煤量，t/h；μt为汽机阀门开度，%；kc为煤量变化的归一化指标，其标称值为1。uB，μt为CCS 模型的输入量u1，u2；PT和机组功率输出Ne（MW）为CCS 模型的输出量。机组功率输出可以通过下式进行计算

由于越来越多的燃煤机组参与深度调峰，为分析机组在全工况范围内的AGC 调节性能，本文展开了30%～100%负荷工况下的分析，CCS 在此区间的典型工况参数见表2。

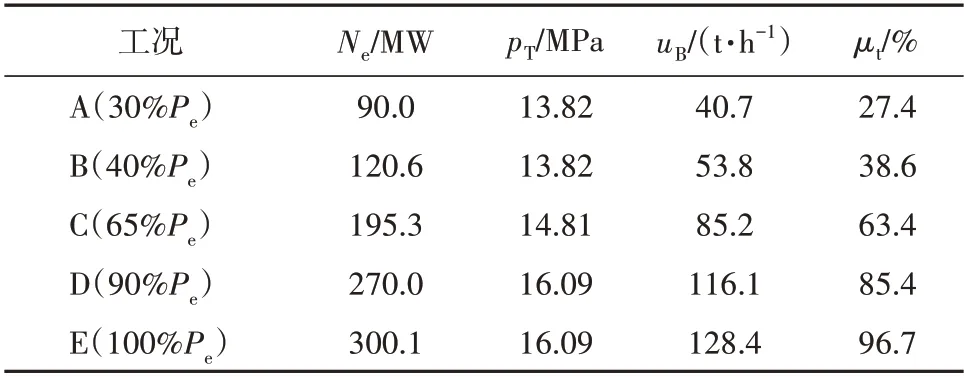
表2 CCS典型工况下的参数Table 2 Parameters under typical CCS working conditions

2.2 CCS变量特性分析

对式（8）描述的CCS 非线性特性、强耦合以及大范围变工况特性进行分析。

对非线性特性采用Vinnicombe 间隙度（νg）进行定量计算［12］，νg≥0.4 时可以认为系统具有较强的非线性［13］。图1 为以工况E（额定工况）和A（超低工况）为基准工况下CCS 的νg分布。由图1可知，无论以工况E 或A 为基准工况，CCS 会多次出现νg≥0.4，意味着CCS具有很强的非线性。

图1 典型工况下νg分布Fig.1 Distributions of νg under different working conditions

采用相对增益矩阵（Relative Gain Array，RGA）分析系统的耦合特性，λij为多变量系统第i个输入到第j个输出的相对增益。表2 中5 个工况的相对增益矩阵分布如图2 所示。由图2 可知，所有工况在不同频率段的相对增益值会有一个明显的转折区间：在低频段，主对角占优，即|λ12|和|λ12|接近1；在中频段，|λij|的值进行转换；在高频段，主对角占优，即|λ11|和|λ22|接近1。CCS具有很强的耦合性，在设计控制策略时必须要考虑回路的耦合作用。

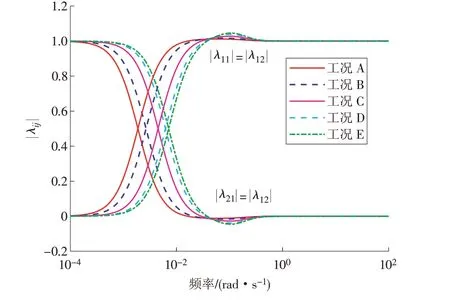
图2 典型工况下|λij|分布Fig.2 |λij|distribution under different working conditions

得到5 个工况下线性化模型的开环阶跃响应，如图3 所示，u1，和u2的阶跃值均为1。从图3 可知，随着工况变化，协调控制系统的动态特性发生了很大的变化，特别是图3c 和3d。此外，由于任一输入量对2 个回路均有明显的影响，说明系统存在很强的耦合作用。需要说明的是，机组在高负荷和低负荷时，即负荷在30%～40%Pe和90%～100%Pe时，采用定压运行；在中间负荷段采用滑压运行。

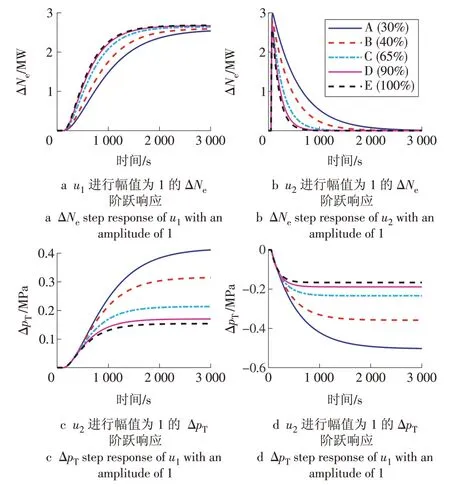
图3 不同工况下系统开环响应Fig.3 Open-loop responses under different working conditions

CCS 常用以DEB 控制结构为基础的控制策略［14］，本文采用的CCS 控制框图如图4所示，其中主蒸汽压力回路的被控量采用热量信号代替主蒸汽压力，热量信号采用下式计算

3 控制器参数对AGC调节性能的分析

CCS 中的控制器为pT回路和Ne回路的反馈控制器GpT(s)和GNe(s)，pT回路的前馈控制器Gff(s)，其中s为拉普拉斯算子，具体控制流程如图4所示。控制器参数结合优化算法与经验调试的方法，得到其标称值：GNe(s) =kp1+ki1/s= 1.95 + 0.11/s；GpT(s) =kp2+ki2/s=50.1+0.025/s；Gff(s)=kpfd+kdfd/(52s+1)=0.35 + 7.84/（52s+1），其中kp1和ki1分别为功率回路的比例增益和积分增益；kp2和ki2分别为主蒸汽压力回路的比例增益和积分增益；kpdf和kdfd分别为功率回路前馈控制器的比例增益和微分增益。

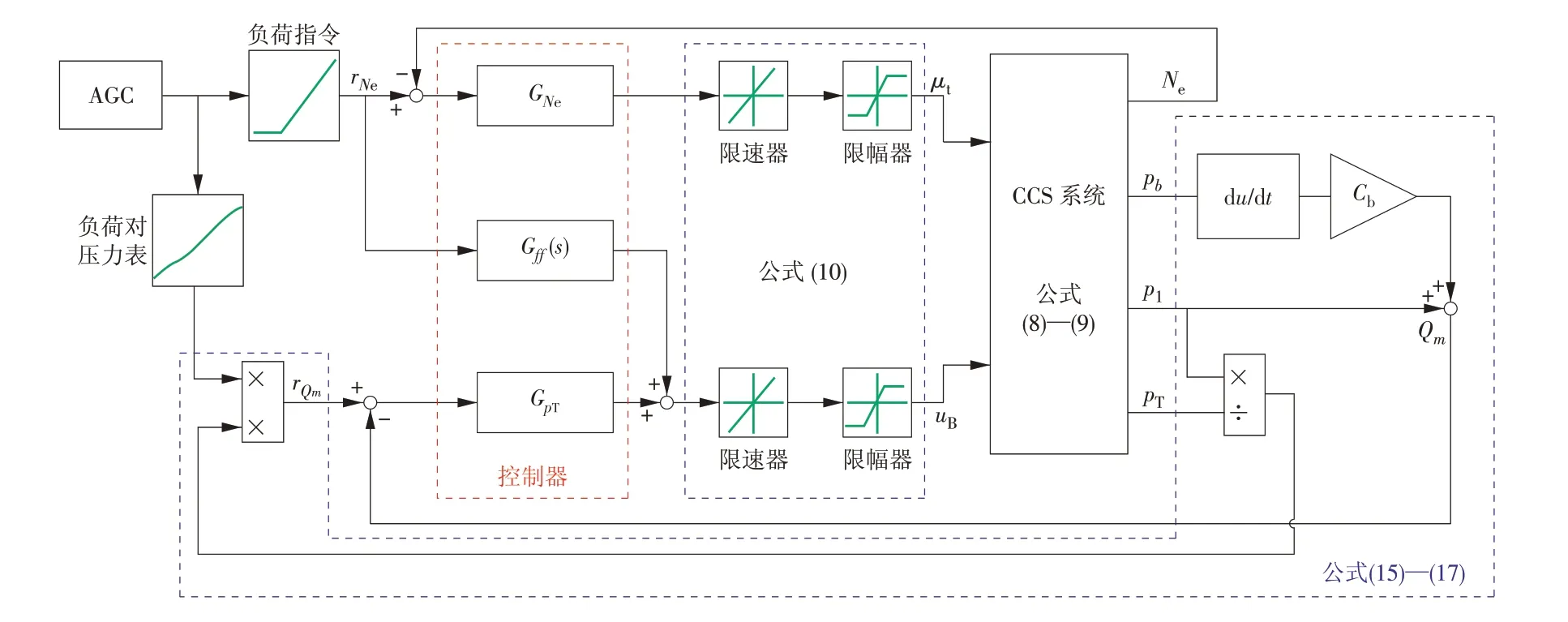
图4 基于DEB的CCS控制流程Fig.4 The control structure of the CCS based on DEB

本节中所有仿真均是基于Matlab 和Simulink 平台展开。此时CCS 的输出和系统控制量分别如图5和图6 所示，可知整个仿真过程中共有5 次AGC 响应过程，包含3 次升负荷和2 次降负荷过程。整定的控制器能够保证CCS 具有满意的控制效果，输出功率能够快速跟踪AGC 设定值，主蒸汽压力在AGC指令变化时会有一定的反调。

图5 标称参数时CCS输出Fig.5 CCS outputs with nominal parameters

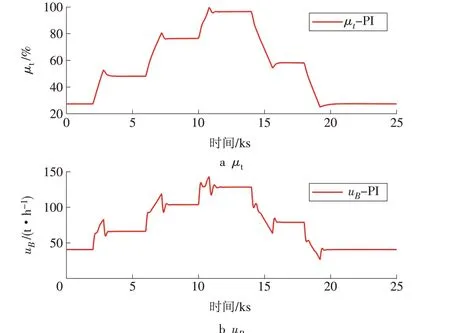
图6 标称参数时CCS控制量Fig.6 CCS control signals with nominal parameters

为了反映CCS 在运行中的各种扰动，设置煤质波动kc= 1 + 0.05 sin(0.01t)，且功率输出存在噪声功率为0.000 1 dBW 的测量噪声。此时，采用单一变量对GpT(s)，GNe(s)和Gff(s)的6个参数进行逐一分析，如图7—12 所示，其中：K i，jm的上标表示第i台机组在j次响应AGC 的动作，下标m为1，2，3 和p，分别表示AGC 调节性能的调节速度、调节精度、响应时间和总性能指标。各自参数的设置变化分别为：kp1∈[0.6，6.0]，ki1∈[0.05，0.15]，kp2∈[20，70]，ki2∈[0.005，0.060]，kpfd∈[0.1，0.6]，kdfd∈[2，12]。需要说明的是，当其中一个参数变化时，其他参数均为标称值。

由图7 可知，kp1会对AGC 的调节性能产生明显影响：随着kp1的增加，K1，j1和K1，j3会逐渐增加，当达到一定程度时，K1，j1和K1，j3的上升速度快速加快；由于K1，j2先 增 加 后 快 速 下 降，导 致K1，jp先 增 加 后 快 速下降。

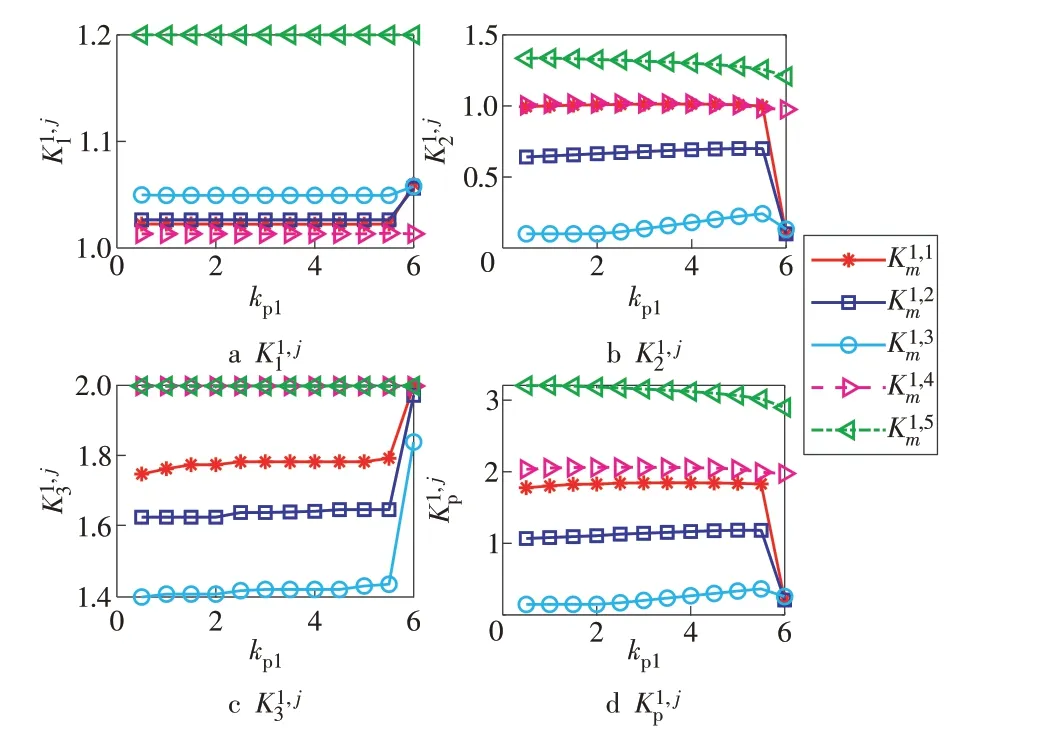
图7 AGC调节性能指标随kp1变化趋势Fig.7 AGC regulation performance indexes varying with kp1

由图8 可知，ki1与AGC 的4 个调节性能指标均呈现正相关，特别是与K1，42和K1，jp的相关性更强。

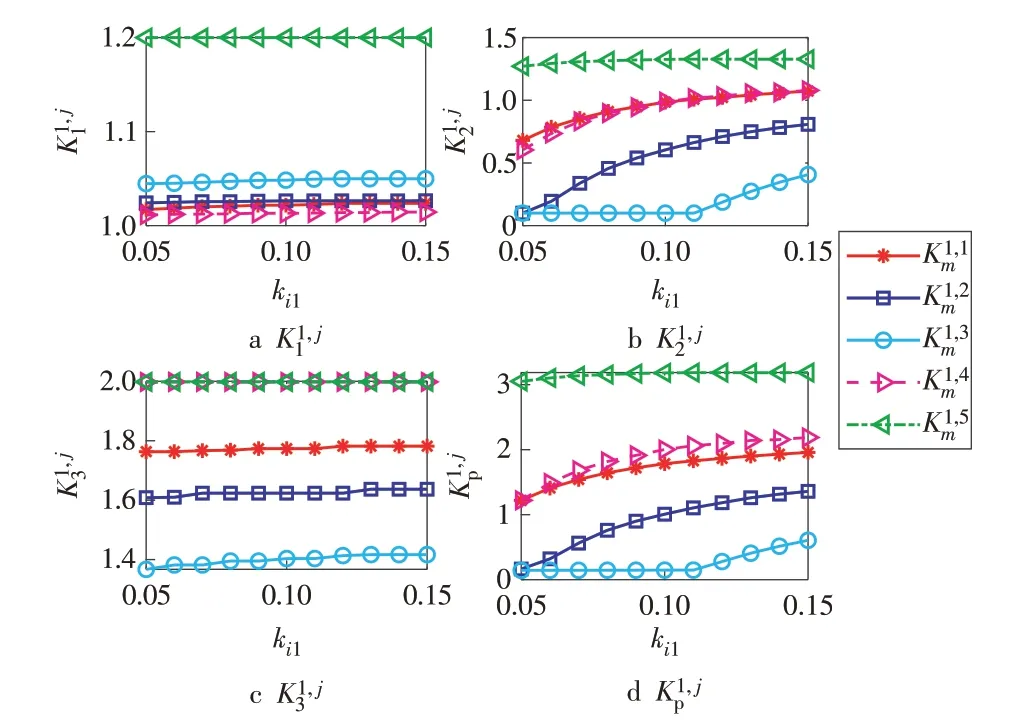
图8 AGC调节性能指标随ki1变化趋势Fig.8 AGC regulation performance indexes varying with ki1

由图9 可知，随着kp2的增加，K1，42表现为明显上升，而K1，41和K1，43的变化不确定，在不同工况下会有不同的趋势，但整体变化幅值较小。由于kp2变化占据K1，jp的 主 导 地 位，使 得K1，jp的 变 化 与kp2保 持一致。

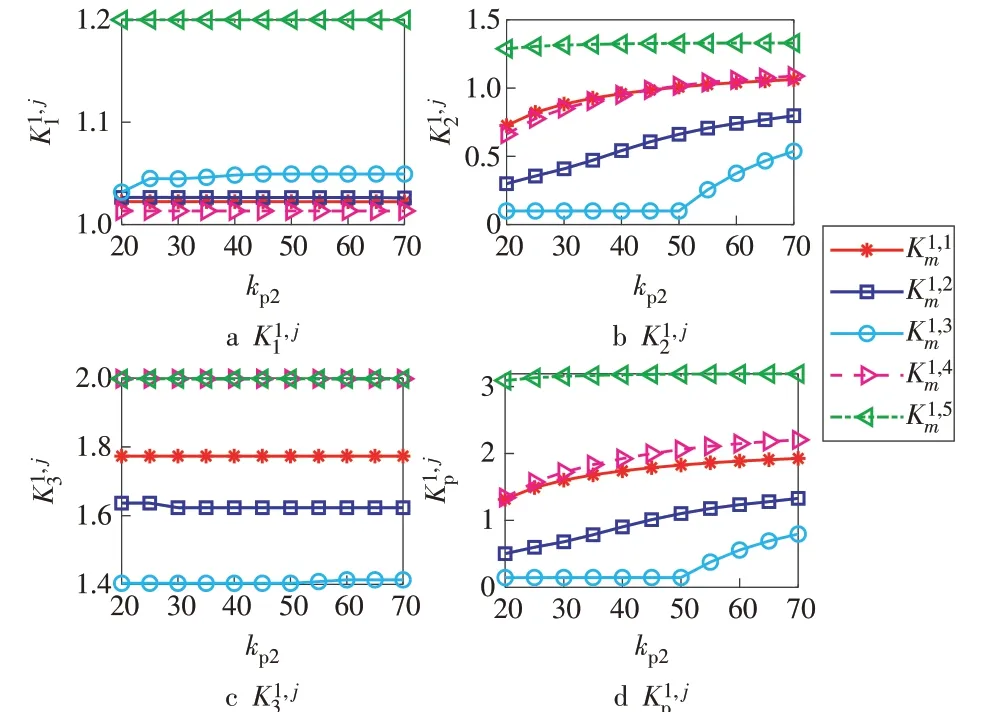
图9 AGC调节性能指标随kp2变化趋势Fig.9 AGC regulation performance indexes varying with kp2

从图10 可知，当ki2在变化范围内，所有AGC 调节性能指标波动较小，在第4 次AGC 响应过程中，K1，42和K1，4p表现为较弱负相关，变化幅值较小。

图10 AGC调节性能指标随ki2变化趋势Fig.10 AGC regulation performance indexes varying with ki2

图11 表明kpfd的变化时，K1，42和K1，4p表现为一定的负相关，和K1，31表现为正相关，在更多的不同工况下与AGC各调节性能指标关联性较小。

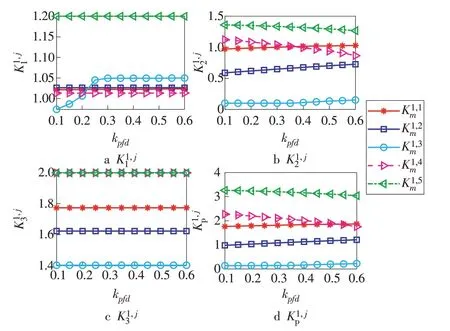
图11 AGC调节性能指标随kpfd变化趋势Fig.11 AGC regulation performance indexes varying with kpfd

图12表明kdfd与所有AGC调节性能指标均未表现有明显的关联性。

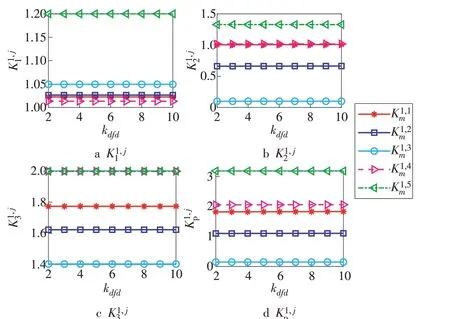
图12 AGC调节性能指标随kdfd变化趋势Fig.12 AGC regulation performance indexes varying with kdfd

总的来讲，kp1，ki1和kp2对AGC 调节性能指标具有明显的关联性。为提高AGC 调节性能，建议适度增加kp1、合理增加ki1和kp2。ki2，kpfd和kdfd对AGC 调节性能指标的影响不明显，在参数调整时，调整ki2，kpfd和kdfd对于提升AGC调节性能作用不明显。

4 结论

本文关注基于DEB 控制结构的控制器参数对于燃煤机组AGC 调节性能的影响。首先对AGC 调节性能指标：调节速率、调节精度与响应时间的定义与计算方式进行介绍。基于此，介绍CCS 模型，并对CCS 的耦合性、非线性等控制难点进行分析。结合直接能量平衡控制结构，在已经优化的控制器参数基础上，通过单一变量法分析控制器参数对调节速率、调节精度与响应时间的影响。

本文主要结论如下：功率回路的比例和积分增益以及主蒸汽压力回路的比例增益对于AGC 调节性能指标具有明显的关联性，为提高AGC 调节性能，可以适度增加功率回路的比例增益，合理增加功率回路的积分增益以及主蒸汽压力回路的比例增益。主蒸汽压力回路的积分增益、前馈回路的比例增益和微分增益对AGC 调节性能指标的影响不明显，调整上述参数对于提升AGC 调节性能作用不明显。

上述结论为提高AGC 调节性能时的燃煤机组控制器参数优化提供了方向性指导，下一步工作考虑将上述结论应用于实际机组的AGC 调节性能优化。