有源电力滤波器直流电压简单模糊比例控制
梁曦文,王映品*,李林,谢运祥
(1.海南师范大学物理与电子工程学院,海口 571158;2.华南理工大学电力学院,广州 510640)
0 引言
目前非线性负载迅速增多使电能质量问题加重,主要是电流谐波、无功负荷与功率因数低。电流谐波不仅恶化功率因数、降低系统效率,而且容易造成设备过热、敏感设备损耗与电容爆炸等问题[1]。因此,电流谐波抑制与功率因数校正非常重要。
有源电力滤波器(APF)是有效补偿谐波与无功电流的装置,它通常由电流滤波器、电力变换器与直流电容组成[2]。
APF控制系统包括电流内环与电压外环。电压外环是保持直流电容电压在参考电压并储能为补偿谐波电流提供能量。因此对直流电压控制相当重要。为了减少能量损失与提升APF 补偿性能,有学者根据不同负载自适应实现低直流电压控制[3-6]。三相四线系统或多电平变换器包含多个直流电容,存在各电容电压保持平衡的控制[7]。文献[7]分别控制上电压与下电压同时保证电压平衡与总电压。
总电压的控制是电压外环的关键[8-9],通常使用比例积分(PI)控制。然而定PI 参数很难同时达到快速响应与精确补偿性能。大量学者提出有关直流电压的控制算法[10-12]。文献[10]提出一种双滑模比例积分算法(DSM-PI)控制APF直流电压,控制器的PI 参数在瞬态时不断切换而在稳态时固定在某值。但这种控制器设计存在很多问题,如没必要瞬态时不断切换PI参数,在稳态时PI参数固定在平均值也不合理。文献[12]在PI 控制基础上建立直流环节的传递函数揭示系统稳定条件,提出变比例积分(VPI)控制器,满足直流环节电压控制的动态特性和稳态补偿性能。当直流环节电压在参考电压附近时PI 值很小,远离参考电压时PI 值非常大,因此存在电压偏移和难以保证稳定的问题。
模糊逻辑是一种工作在输入不精确且处理非线性的鲁棒算法。模糊逻辑将语言逻辑控制与描述的模糊关系用于精确的模型。很多学者将模糊逻辑控制用于APF[13-18]。
文献[15]提出一种模糊比例加卷曲积分算法用于三相APF 电流控制。文献[16]提出模糊逻辑用于电流与电压控制,控制器有49个模糊规则。文献[17]在模糊逻辑控制中产生反向信号消除三相APF 直流电压超调与未达参考值,然而在瞬态时很难生成精确的反向信号。文献[18]所提算法与文献[17]一样,只是用于单相APF。文献[19]提出一种模糊逻辑控制器用于APF 直流电压控制,并在电网不平衡工况下补偿谐波与无功。文献[20]提出的模糊逻辑控制器基于直流电压的误差与误差变化估算参考电流峰值,该构建需要49个多输入单输出(MISO)模糊规则,算法复杂还没有根据最优化原则。
直流环节电容必须提供有功功率补偿谐波电流,因此直流环节电压的脉动稳态是不可避免的。根据比例积分控制器的原理,如果比例系数Kp太大就会注入大量谐波电流源电流,严重影响电源电流的补偿性能[21]。
通过分析得到最优控制参数是在瞬态时,为了快速收敛,比例增益Kp应该较大;在稳态时,为了提高谐波抑制性能,Kp应该较小。
因此,本文基于广义逼近的模糊控制提出一种简单模糊比例控制算法调节直流电压。该算法遵循以上的目标实现比例增益Kp在瞬态时较大;在稳态时较小。另外,该模糊算法只有3条规则,非常简单,经过仿真与试验验证该算法的性能较好。
1 三相LCL有源电力滤波器电路
三相LCL 有源电力滤波器电路如图1 所示。图中,udc为直流电压;Cdc为直流电容;L1/R1为变换器侧L滤波阻抗;L2为电网侧L滤波阻抗;C为滤波电容;Vcx为变换器输出电压;ipx为变换器输出电流;icx为APF 补偿电流;iL为负载电流;usx为电源电压。下标x代表a,b,c相。
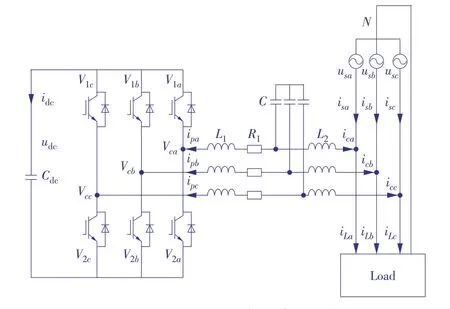
图1 三相LCL有源电力滤波器电路Fig.1 Circuit of a three-phase LCL APF
2 直流电压控制分析

2.1 直流电压与补偿性能的关系
由图2 分析d轴电流分量,在理想情况下电流跟踪误差ied=0,有
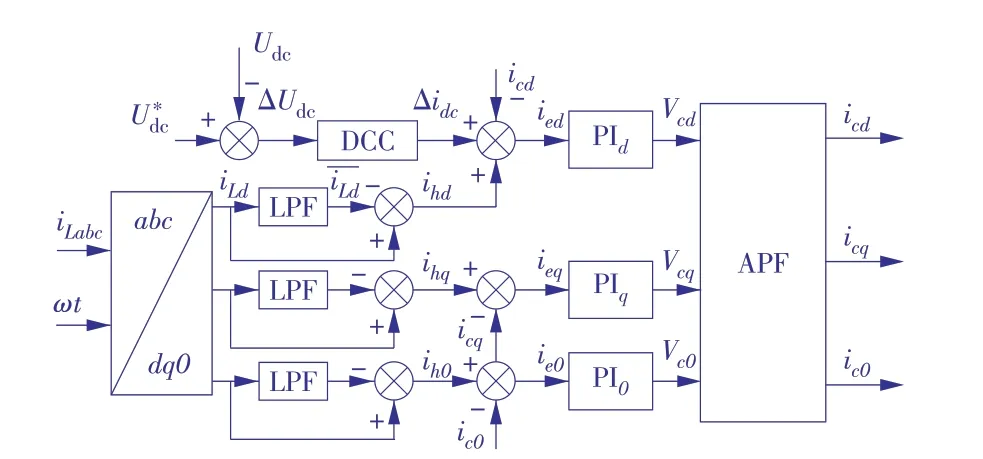
图2 APF控制系统Fig.2 Control system of an APF

理想的补偿电网电流isd应该等于负载直流分量iˉLd。忽略检测误差,电网电流的谐波都是由直流电压的调节电流Δidc注入的。

综上分析,直流电压偏差ΔUdc与直流控制器输出Δidc、补偿电流icd的积分成正比。因此只要有谐波补偿直流电压就会有波动,这是不可避免的。由于主要谐波是5 次与7 次,所以直流电压的波动主要是6次基波。
从式(4)与式(5)可知,较大的比例系数Kp会给电网电流注入较大的谐波电流。
2.2 直流控制器在瞬态时的影响分析
现有的直流控制研究多数都采用了P/PI 控制,下面分析PI参数在瞬态时的影响规律。
2.2.1 PI控制器比例系数Kp对系统的影响
仿真中设定在t=0.1 s时减小负载,在t=0.2 s时改变参考电压,设定积分系数Ki=0 时在一系列比例系数Kp下进行仿真,研究APF 的直流电压在补偿初期、负载突变与参考电压变化工况下系统的响应特性。最终仿真数据结果如图3 所示。图中Kp02,Kp05,Kp1,Kp2,Kp5,Kp10,Kp20分别代表Kp=0.2,0.5,1.0,2.0,5.0,10.0,20.0。
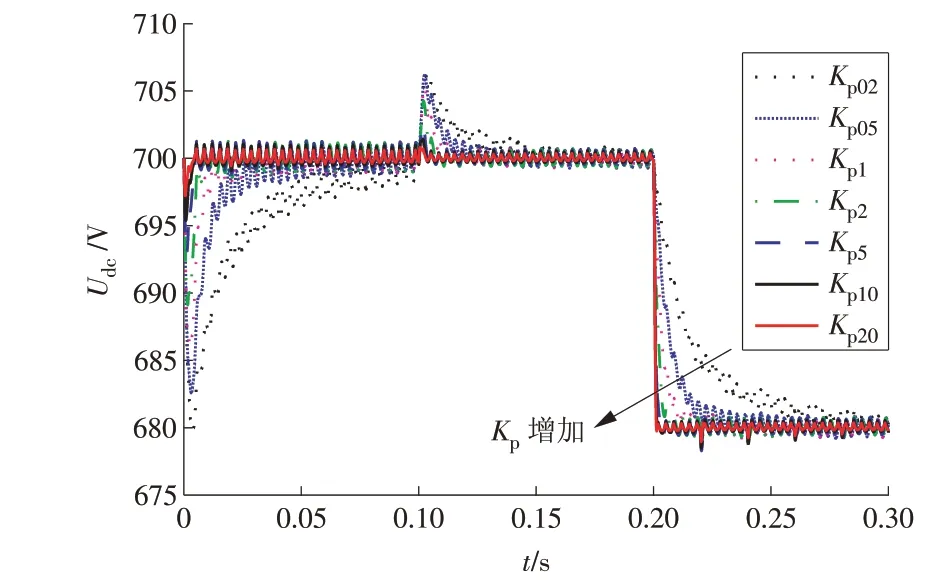
图3 比例系数Kp对系统的动态影响Fig.3 Influence of Kp on dynamic characteristics of the system
由图3 可知,如果比例系数Kp增大,APF 在补偿初期、负载突变与参考电压变化时直流电压的响应速度将加快,而且不会超调。
2.2.2 PI控制器积分系数Ki的分析
补偿系统在t=0.1 s时减小电阻负载,在t=0.2 s时降低直流参考电压,设定比例系数Kp=0.5 时分析积分系数Ki对直流电压在补偿初期、负载突变与参考电压变化阶段的影响曲线。仿真结果如图4 所示。图中Ki1,Ki10,Ki100,Ki1000分别代表Ki=1,10,100,1 000。
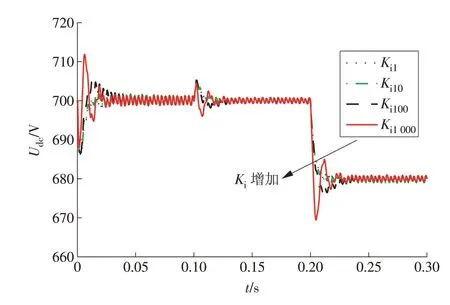
图4 积分系数Ki对系统的动态影响Fig.4 Influence of Ki on dynamic state of the system
从图4 中可以看出,增大积分系数Ki的值,补偿初期、负载突变与参考电压变化时的响应速度加快了,但也造成超调量加大。该系统参数变化的特点符合二阶系统。
2.3 直流控制器在稳态时的分析
在稳态时电网电流的谐波是一个重要的评价指标,下面分析PI参数在稳态时的影响规律。
2.3.1 不同比例系数Kp的谐波含量分析
采用不同的比例系数Kp分别进行仿真,应用Matlab 自带的FFT 工具分析仿真结果在稳态时的电流频谱,提取低频谐波与开关谐波(SW)数据,如图5所示。
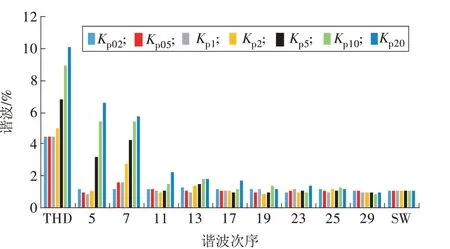
图5 不同Kp仿真时的谐波分布Fig.5 Harmonic components with different Kp
由图5可知,当Kp=0.5时的总谐波值最小,等于4.42%,加大比例系数Kp时,总谐波畸变率(THD)值明显升高,特别是5,7次等低次谐波,高次谐波变化不明显。
2.3.2 不同PI积分系数Ki的分析
设定比例系数Kp=0.5 时,对一系列积分系数Ki分别进行仿真,然后用Matlab 自带的FFT 工具提取稳态时的电网电流频谱,提取的谐波数据如图6 所示。图中Ki0代表Ki=0。
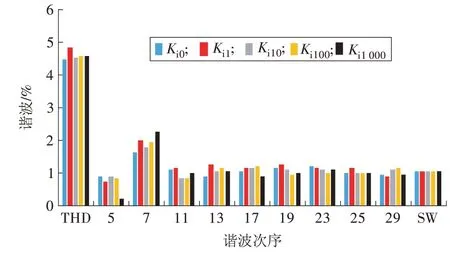
图6 不同Ki时的谐波含量Fig.6 Harmonic components with different Ki
由图6 可知,随着积分系数的改变对稳态的电流谐波变化不大。
通过以上参数的影响规律分析可知,如果用比例(P)控制器,在任意参数下直流侧电压都不会超调。当比例系数Kp增大时,直流电压响应速度会加快但同时电流谐波含量也会增大;而加大PI 控制器的积分系数Ki,则会提升直流电压的响应速度,但同时也会加大直流电压超调,而对稳态时的谐波补偿影响不大。
由以上理论与仿真分析可得出直流侧电压控制策略:在瞬态时增大Kp,使电压快速响应;在稳态时减小Kp,减少电压谐波注入电网电流。
3 所提控制算法
经上述分析得出,APF 直流侧控制器最优算法应该在瞬态时具有较大的比例系数,使动态响应快速;在稳态时实现较小的比例系数,降低电网电流谐波。目前常用的PI 控制难以实现该要求,而最近一些学者提出的变PI 控制也没有很好地达到该性能。
本文基于模糊控制理论,提出了一种简单模糊比例(SFP)控制器来控制APF 直流侧电压。模糊输入信号取直流电压偏差值ΔUdc,模糊控制输出是比例系数Kp。所提的直流侧SFP 控制系统示意如图7所示。该算法基于模糊控制算法,独特之处是设计模糊控制器时根据参数影响规律与最优的输入输出关系。所设计的模糊算法隶属关系集合物理意义明确,并实现了最简洁的模糊关系实现预期输出效果。
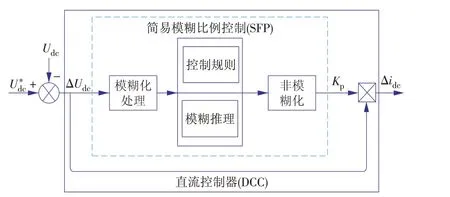
图7 APF直流侧控制系统示意Fig.7 DC-link voltage controller of the APF
所提SFP 模糊控制器主要由4 部分组成:模糊化处理、控制规则、模糊推理、非模糊化。下面详细介绍各部分的功能与设计过程。
3.1 模糊化处理
该控制模糊变量直流电压误差数值化的方法如图8 所示。该模糊器的隶属函数由2 个三角形和3 个梯形单元构成,将这5 个单元命名为负大(NL)、负小(NS)、零区(ZE)、正小(PS)、正大(PL)。物理意义:ZE 为电压误差较小,表示在稳态;NL 和PL 为误差较大,表示在瞬态;NS 和PS 为瞬态与稳态的过渡段。模糊化映射关系为


图8 输入变量ΔUdc的模糊化隶属函数图形(截图)Fig.8 Fuzzy membership function with input variable ΔUdc(screenshot)
3.2 控制规则
该模糊控制的输出是直流控制器的比例系数Kp。输入信号是直流电压偏差ΔUdc,所以该模糊规则是为了实现Kp与对应ΔUdc的映射。因为ΔUdc分5个单元,且Kp的取值只与ΔUdc的绝对值有关,所以只要3 条规则就可以。将其关系用模糊规则的ifthen语句表达,SFP控制器的模糊规则见表1。
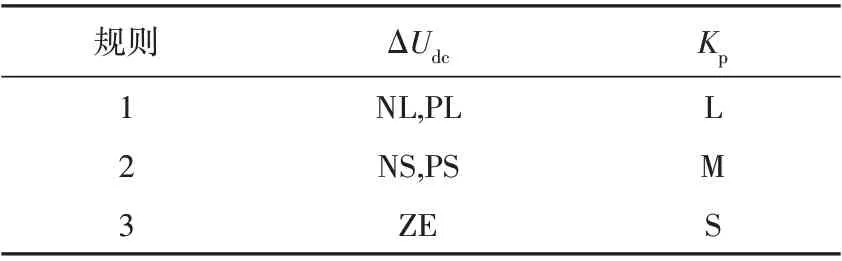
表1 SFP控制器的模糊规则Table 1 Fuzzy rules of the SFP controller
3.3 模糊推理与非模糊化
所提SFP 控制器只要3 条简单的模糊规则。本模糊控制器算法采用Mamdani最小推理机。该推理机简单且物理意义明确,而且操作方法可以通过直接获得。
输出变量Kp的清晰化隶属函数图形如图9 所示。拟采用重心法进行解模糊化。计算比例系数Kp重心法(COG)的值为

图9 输出变量Kp的清晰化隶属函数图形(截图)Fig.9 De-fuzzy membership function with output variable Kp(screenshot)

式中:μ(Kpi)为Kpi参数的隶属度;Kpi为Kp集计算出的点值;COG值为Kp的数值;m为集合的数量。
按照以上4步运算得到输入输出对应关系的精确曲线,如图10所示。所获得控制器的比例系数Kp在稳态时(ΔUdc为ZE区)取较小值;在瞬态时即电压偏差超过稳态值时Kp迅速增大,并限制了最大值。
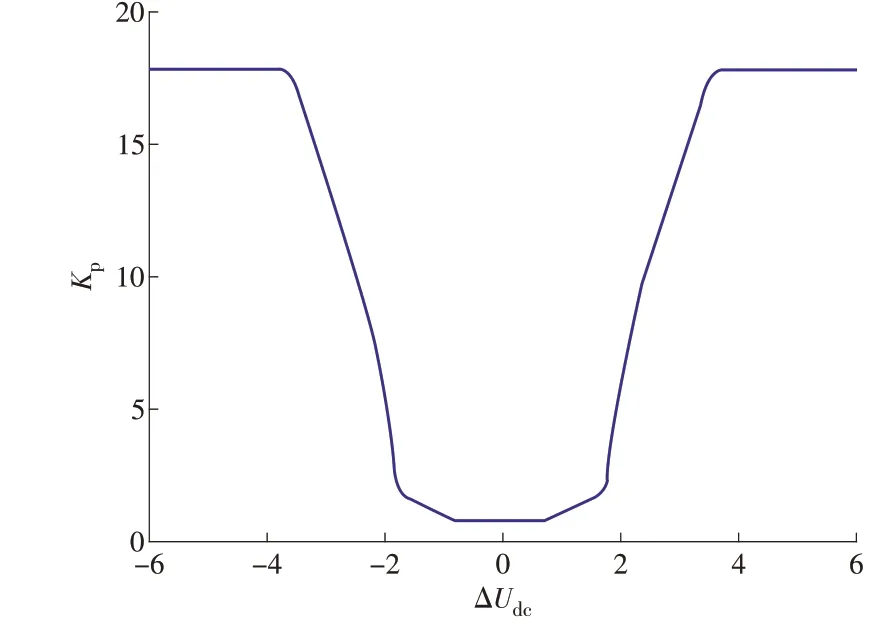
图10 SFP控制器的输出曲面观察器Fig.10 Curved observer for the output of the SFP controller
4 仿真分析
应用Matlab/Simulink 建立模型仿真,输出接的三相不控整流器负载是阻性负载,APF 控制器的电流环是PI 控制,PI 控制器的参数是Kp=4,Ki=200,APF 系统参数见表2。仿真对比分析了直流侧采用VPI 控制器[9]与PI 控制器算法的仿真结果,分析该控制器的特性。
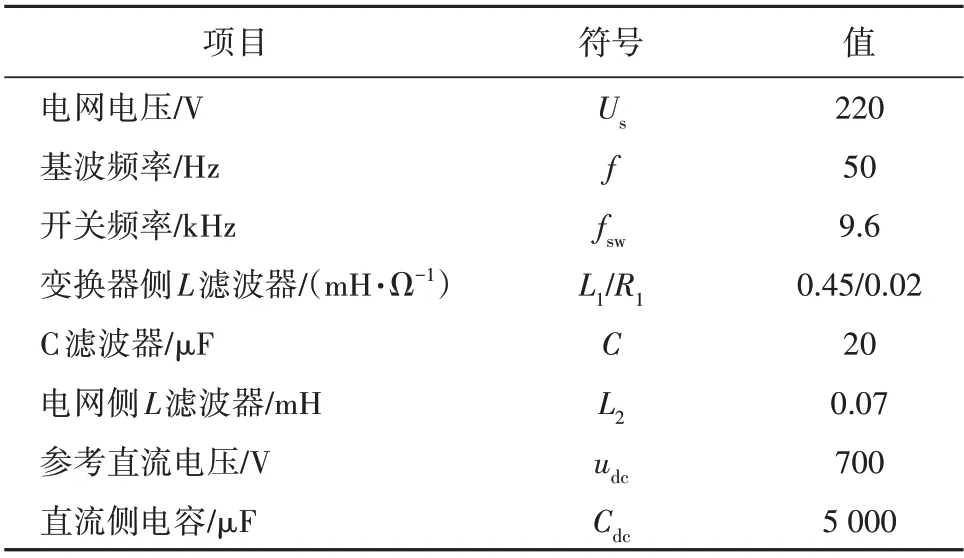
表2 APF系统参数Table 2 APF system parameters
直流侧采用VPI 控制器时,PI 参数按照Kp=0.5|ΔUdc|,Ki=10|ΔUdc|。采用PI 控制器时的参数设Kp=0.5,Ki=10。
仿真在时间t=0.1 s时减小负荷,在t=0.2 s时把参考电压变到680 V。对比3 种控制算法的直流电压如图11所示,对比电网电流曲线如图12所示。
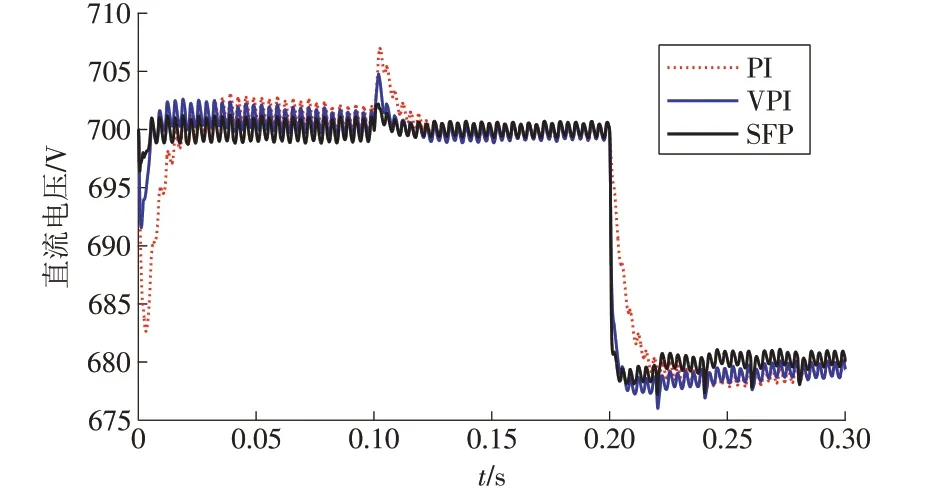
图11 直流电压对比Fig.11 Comparison of the DC-link voltage

图12 补偿后电网电流对比Fig.12 Comparison of the compensated source current
在图11中初始阶段与负载变化时,所补偿的参考电流发生较大变化,对直流侧电压产生一定冲击。
当用定PI 控制器时,直流侧电压收敛时间长且偏差较大;当用VPI控制器时,直流电压响应速度较快且冲击较小,但稳态电压与参考电压有一定偏差;而使用所提的SFP控制器,直流电压响应快波动较小,且稳态电压基本没有偏差。
在减小负载时,所提SFP 控制算法的直流电压响应性能最好,稳定时间为0.010 s,超调量为2 V。采用VPI 控制器的稳定时间为0.012 s,超调量为5 V。采用PI控制器的性能最差:稳定时间为0.023 s,超调量为7 V。
在t=0.2 s时把原来直流电压700 V参考电压变到680 V,所提SFP 算法稳定时间为0.003 s,最大误差为2.0 V。采用VPI 控制器的稳定时间为0.004 s,最大误差为2.8 V。采用PI 控制器的性能最差,稳定时间为0.018 s,最大误差为2.2 V。
由图11 可知,SFP 控制器在突变状态比例系数较大时能够使直流电压快速达到稳定,而在稳态时比例系数较小,直流电压的纹波也较小。
由图12可知,采用各种控制算法补偿后的电网电流在稳定时THD 相差不明显,因为所设计的比例系数比较接近,但动态响应特性差别较大,所提SFP控制器有独特的优势。
稳态时,对比各直流控制器电网电流的THD 值见表3。

表3 各控制算法的电网电流THD值Table 3 THD value of the source current obtained by different algorithm %
由表3 可知,设置的所有控制算法都可以补偿到电网电流达到IEEE 519—2014 标准的5%以下。SFP控制算法在各种工况下的谐波THD值均小于PI控制与VPI控制。
图12 也说明了SFP 控制器在突变状态比例系数较大,电流能够快速达到稳定,而在稳态时比例系数较小,因此直流纹波注入电网电流的谐波含量也较小。
综上所述,所提SFP 控制算法在稳态时与瞬态时的性能均较好,实现了稳态时谐波较小、瞬态时响应速度快且没有超调。
5 试验结果与分析
为了验证所提APF 直流侧SFP 控制算法,编程并搭建了三相三线APF 试验平台,核心控制器用TI公司的TMS320F28335 芯片,试验采用Tektronix 示波器进行数据采集,试验采用参数与仿真相同,试验装置如图13所示。

图13 三相APF试验样机Fig.13 Prototype of the three-phase APF
5.1 在负载突变工况
在负载电阻由10 Ω 变到20 Ω 时,采用PI 控制与所提SFP控制器的试验结果如图14、图15所示。
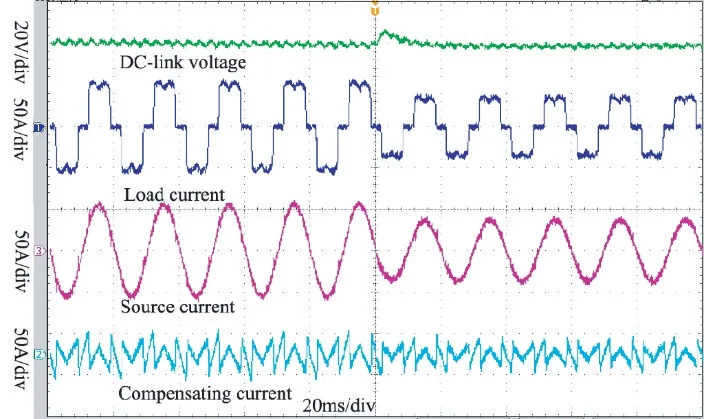
图14 PI控制器在负载变化时的试验结果(截图)Fig.14 Experimental results of the PI controller with variable load(screenshot)
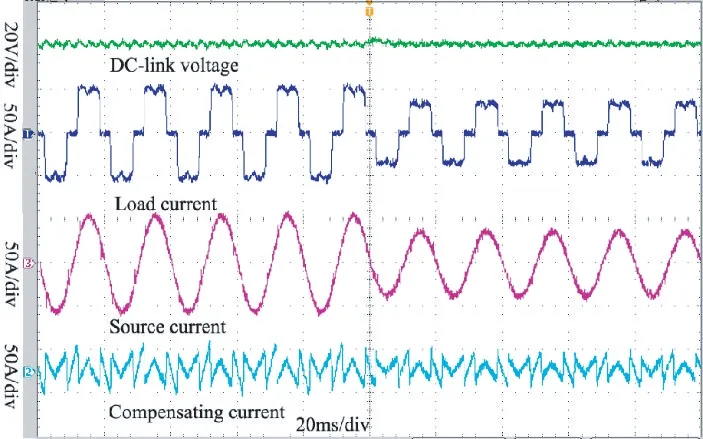
图15 SFP控制器在负载变化时的试验结果(截图)Fig.15 Experimental results of the SFP controller with variable load(screenshot)
对比图14 与图15 可知,当负载变化时采用PI控制器的系统直流侧电压波动较大、稳定较慢。而采用SFP 控制的系统直流侧电压波动较小、稳定快速。采用所提SFP 控制的电网电流响应较快,且较接近正弦波,PI 控制与SFP 控制器测得的THD 分别为4.92%与4.71%。
5.2 改变参考电压工况
当设定直流参考电压值由700 V变到680 V时,采用PI 控制与SFP 控制测得的试验结果如图16、图17所示。
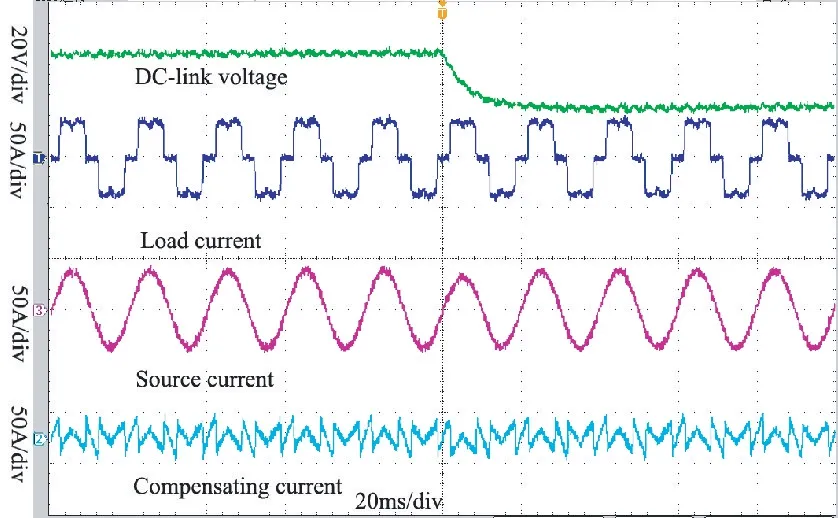
图16 PI控制器在参考电压变化时的试验结果(截图)Fig.16 Experimental results of the PI controller with variable reference voltage(screenshot)

图17 SFP控制器在参考电压变化时的试验结果(截图)Fig.17 Experimental results of the SFP controller with variable reference voltage(screenshot)
对比图16 与图17 可得,采用PI 控制时直流侧电压需要较长才能时间达到参考电压值,而采用SFP 控制能够快速达到电压值。采用SFP 控制电网电流也能够快速稳定,测得PI 控制与SFP 控制的THD分别为4.86%与4.64%。
6 结论
本文分析了直流电压的机理并提出一种SFP控制算法进行直流电压控制。
通过仿真对比PI 控制与VPI 控制,从结果可以得出所提控制算法在稳态时谐波抑制好,在瞬态时响应速度快。并通过试验对比PI 控制,所提算法简单,适用范围广,能够推广到其他系统抵抗瞬态干扰与提高稳态性能。

