以学生为中心的高中数学课堂设计——“直线与圆的位置关系”复习课

江苏 段赛花

习总书记在党的十九大明确提出加快建设创新型国家.本文以学生为中心设计高中数学课堂，尝试让学生站在系统高度上俯视数学，让课堂更开放、更多元、更创新.以学生为中心的课堂设计采用“三看一注意”：一看，几何问题代数化(解析几何本质)；二看，几何问题几何化(看图秒杀)；三看，几何问题向量化(2008年引入教材)；一注意：数形一体，动静结合.从一题多解到多题一解，始终以学生为中心展开变化.

笔者的课堂每一道题都有甲乙两名学生与一名老师讨论，解题应当自出机杼，想出自己的解法.首先，要不断总结，琢磨已有解法，从细微处开始留心，看看能不能省去一两步？能不能换一个角度？能不能将条件减弱或结论加强？很多时候，递进式命题会拿去第一问，直接让学生思考第二问，倘若学生毫无反应，再把第一问添加上去.整个习题解完以后一起回头再看.变一变，编一编，解一解.最高境界，一堂课只解一道题，一道题包含整个单元知识.有时候循着学生的思路前进，得出新的解法，当然很好，如果走下去，发现此路不通，到不了目标，那也很好，知道了这条路走不通，不再坚持也是一种收获.

笔者班级内有一个特别喜欢钻牛角尖的学生，首先需要肯定他的想法，鼓励他找到简单而一般的解法，即使已有好的解法，也应注重研究其他思路：还可以从何入手？有哪几个关键步骤？解决问题的办法之一就是不断变更问题，直到它变得容易处理.如若将结论当做已知，虽然原命题成立，逆命题不一定成立.但在有某种唯一性时，可以同时成立，这种方法是同一方法.有时候还会用原命题的等价条件逆否命题来研究问题，获得一种崭新境界.本文中的“秒杀”法在填空、选择题中让学生能够高屋建瓴、一眼看穿.

一、课堂以学生为中心，如何选择经典题

有效的数学教学需要学生积极地参与自己的学习过程，也就是要求学生扮演一个主动学习者的角色，通过事物的本质可以知道这在整个事件中的作用和运作规律.首先，教师要担当学生数学学习促进者的角色，不断激发学生与生俱来的自主数学学习的意识；其次，教师要促进学生自主“守法”“用法”“立法”，让学生逐步形成“自适应”的数学学习策略与方法.选题要吻合“三看一注意”.

抛出问题：已知圆M:x2+(y-6)2=16,点P是直线l:x-2y=0上的一个动点,过点P作圆M的切线PA,PB,切点分别为A,B.

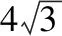
(2)若△PAM的外接圆为圆N,试问:当点P在直线l上运动时,圆N是否过定点?若过定点,求出所有的定点的坐标;若不过定点,说明理由;

(3)求线段AB长度的最小值.

解析：(1)学生1：由题意知,圆M的半径r=4,圆心M(0,6),

∵PA是圆的一条切线,∴∠MAP=90°，

(2)学生2：圆N过定点.

设P(2a,a),∵∠MAP=90°,∴经过A,P,M三点的圆N以MP为直径,

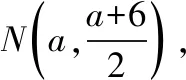
即x2+y2-6y+a(-2x-y+6)=0,

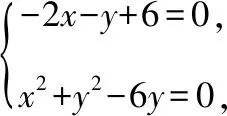
学生3：直径式方程更快，从严谨性角度，需要用向量证明一下.

即x2+y2-2ax-ay-6y+6a=0 ①,

圆M:x2+(y-6)2=16,

即x2+y2-12y+20=0 ②,

②-①得2ax+(a-6)y+20-6a=0,

即为直线AB的方程.

学生5：等面积法

至此，初步达到“三看一注意”，学生的解法殊途同归，都转化为与|MP|有关的问题，实现两个动点化归为一个动点的问题，以静制动.一题多解，为变题铺垫，更为学生编题埋下伏笔.

二、课堂以学生为中心，如何建构深度学习

一是要强调过程性学习；二是要强调挑战性学习；三是要强调创造性的学习.“数学教育是数学的再创造.”数学学习实际上是一种通过不断质疑与探究，发现、理解、消化、应用、整合、创生新知的过程.

从变题开始，用“三看一注意”引导，实现多题归一.

学生8：求切线长|AP|的最小值.

有学生9追问了为何不是求最大值.通过学生8的解答，恍然大悟.

学生10：求S四边形AMBP的最小值.

因为学生9的追问，此处不再有学生提出求最大值的问题.

学生10说，是学生5给了他灵感.

学生11：求∠APB的最大值.

师：“你是怎么想到的？”

学生11展示点P在直线上的运动，看张角变化.先猜想再论证，把“三看一注意”的第二看演绎地很完美.解析几何本质上还是几何问题.

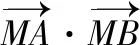
编题需要反复推敲，数字的设计，答案的美丽，知识点的融会贯通均需考虑在内.倘若学生能掌握“三看一注意”，能够站在命题人的角度思考问题，一定能够高屋建瓴，从系统的高度俯视数学.开放题的编题更具挑战性，编一编，解一解，再修一修.远离题海才能更胜一筹.把学生往前推，老师慢慢往后退，课堂是属于学生的.

学生15：求直线AB过定点问题.他用两圆方程相减得到直线AB方程，再转化为恒成立问题.此处，教授“秒杀”方法，用类比推理.

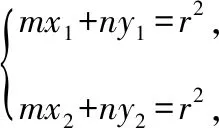
问题由学生提出，教师需提升“三看一注意”的第一看，突出解析几何的本质：几何问题代数化.

三、课堂以学生为中心，如何注重知识的整体性与关联性

利用“三看一注意”，以相关关系的视角审视数学知识的发展，以关联的方式去学习，在似乎没有关系的知识之间架起一座座桥梁，在相关性中拓展学生的思维，引导学生完整地经历问题的提出和问题解决及数学思想方法的提炼和概括过程.

挑战题：(2012·苏州大学高考预测卷)若实数a,b,c成等差数列，点P(-1,0)在动直线ax+by+c=0上的射影为M，点N(3,3)，则线段MN长度的最大值是________.

传统解法消参，找出定点A(1,-2)，寻找到AP为直径的隐形圆，转化为定点到圆上点的距离问题，找到圆心不动是关键，以静制动.学生16从结构a-2b+c=0中比较直线方程直接看出定点A，值得肯定，这便是数学的直觉.进一步揭秘命题人的意图，为他们自己编出高质量的习题埋下伏笔.几何画板的运用，提升学生深刻领悟“三看一注意”的注意：数形一体，动静结合.

一节课的总结特别重要，围绕点在圆上运动和点在直线上运动，从点到线再到面，拓展到两圆问题，运动中蕴含不变，最后回归到2019版人教版A选择性必修第一册99页的15题：已知点P(-2,-3)和以点Q为圆心的圆(x-4)2+(y-2)2=9.

(1)画出以PQ为直径，点Q′为圆心的圆，再求出圆Q′的方程；

(2)设圆Q与圆Q′相交于A，B两点，直线PA，PB是圆Q的切线吗？为什么？

(3)求直线AB的方程

第三问中再试一次“秒杀法”，让数学直觉来得更猛烈一些.学生编题不能全面总结，可以再添如下经典,

已知圆C:(x-1)2+y2=r2(r>0)与直线l:y=x+3.

(1)若直线l上有唯一的一个点P，使得过P点作圆C的两条切线互相垂直，求r；

(2)若r=2，且直线l上存在点P，过点P作圆C的两条切线夹角为60°，求点P的横坐标.

答案：(1)2;(2)P(-3,0)或(1,4)

本节课紧紧围绕“三看一注意”，激发了学生提出问题，研究问题的兴趣.演绎数学本质：大胆猜想，小心求证.研究解析几何最重要的方法是坐标法、综合法、向量法.在千差万别之中，存在着保持固定不变的形态的事项.抓住本质，就能以学生为中心设计出创新型的数学课堂.正如苏东坡面对奔流不息的江水和永不休止的月亮圆缺交替变化，在《赤壁赋》中唱到：逝者如斯，而未尝往也；盈虚者如彼，而卒莫消长也.宇宙万物，若既从变化的方面去看它，同时又从不变的方面去看它，就会看到如苏东坡所说的那种情形.从一方面去考查它，会看到它是瞬息万变的，而若从另一方面去考查它，只会看到这种变化的内部，却俨然存在万世不变的实体.

老师眼中心中都要有学生，专业能力极强的老师，课堂设计特别完美，若一个人讲得滔滔不绝，眼中能看到学生，但不太理会学生的思维，按照自己设计的程序行云流水，一气呵成，这课是讲给专家听的，倘若来个外行呢？讲得外行也明白，才是本事.浅入深出，层层递进，等一等学生的灵魂.课堂的关键是学生领悟，哪个来听课，都要初心不变.老师是为学生服务的，心中有学生，站在他们的角度，慢一点又何妨？学生想不出，等；学生算不出，等.学生的潜能无限.课堂上，等一等，就有很多新的发现；有学生想出各种解法，有学生计算卡住，点拨一下，老师几乎不用讲，学生兴致勃勃来板演，问题就暴露出来了.