基于RBF神经网络的短时降水量预测方法研究*

张启凡 王永忠 马俊逸

（1.中国商飞民用飞机试飞中心 上海 201323）（2.中国民用航空飞行学院 广汉 618300）

1 引言

对流天气是我国夏秋两季多发的天气现象，短期的强对流天气受到地理条件等多种因素的影响，在预报上有很大的难度，且易产生各类气象灾害［1］。针对降水量预测问题，研究人员提出了多种的预测方法。传统降水量预测大多采用数值预报方法［2］，张祥［3］等提出的加权型马尔科夫模型，屈文岗［4］等基于滑动平均马尔可夫预测模型。李文辉［5］等提出时间序列均生函数模型。陈程［6］提出了一种结合卷积神经网络和GRU得到了Conv GRU模型。Qing-hua Miao等［7］结合卷积和长时记忆神经网络改进季风降水预测。

诸多研究中鲜有用影响降水的气象指数或因子对短时降水量进行数值预测。本文从物理量参数回归分析的思想出发，选取并计算了影响降水的物理参数。综合这些物理量参数利用多元线性回归模型和拟合效果较好的BP神经网络、RBF神经网络模型对短时降水量进行预测并对得到的仿真结果进行误差分析，从而选取最优的预测模型。

2 数据的获取与处理

降水数据选用北京怀柔区2007年1月1日至2017年12月31日的地面逐日降水资料。基础物理量参数由美国国家环境预报中心（NCEP/NCAR）每天四次更新的（2.5°×2.5）再分析数据下载得到nc数据文件，本文使用Matlab中相关函数对其进行读取。在对nc文件中var数据进行读取之前需要将该地区的经纬度坐标做格点化处理方可进行读取从而获取研究所需的基本物理变量。经同化处理前的降水数据如表1所示，格点坐标数据如表2所示。筛选2007～2017年间共计180组数据编入训练集。

表1 降水样本示例（地球坐标）

表2 降水样本示例（格点坐标）

3 基于多元线性回归的降水量预测模型

3.1 多元回归模型变量的选择

多元回归模型有三个主要特征：线性、方差齐性、残差为正态分布［8］。在实际预测问题中通常很难判定一个变量是相关的，理想的模型需要尽可能低的残差，又需要有尽可能少的变量。故在选择变量时将尽可能减少待估计回归系数的数量并参考因变量之间和因变量与自变量的物理关系。

结合降水产生过程的物理量方程，综合考虑强降水产生的三个必要条件，充沛的水汽，大气的动力和大气稳定度。选择q、RH、|FH|、FZ、∇p·六项物理量参数建立模型。

上述指数的相关计算公式如下：

通过Matlab编程读取格点坐标信息下的nc数据集中的变量参数并计算上述指数，整理为模型的输入数据集共180组，随机选取30组作为测试集。

3.2 多元线性回归预测结果及评价

依据上述参数及数据建立多元回归模型并进行预测以及检验分析，所得结果如表3所示。

表3 多重判定系数

R、R2，调整R2反映线性回归方程拟合度，取值范围为0至1，越接近1拟合度越好。

由F检验的结果，sig=0.000＜0.05表明支持原假设，也就是线性回归方程显著。

由t检验的系数得到回归方程：

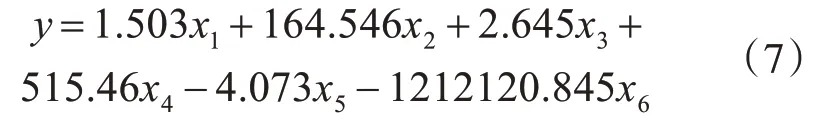
在得到回归方程之后还需要考虑这些数据是否适合做回归即它们之间是否存在线性关系。

图1中横坐标为降水量的标准化预测值，纵轴代表实际降水量。图中的数据点为使用线性回归模型进行预测得到的降水值。理想情况时，预测点均匀分布在图中黑色直线两端，所以可以看出该模型的精度不够理想，由于数据中包含降水量为0的情况，所以选用MAE，MSE，RMSE对误差做出评价。

图1 线性回归模型预测

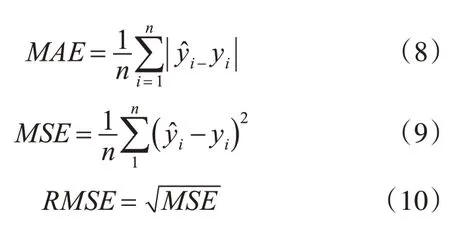
表4 预测效果评价

上述指标显示多元线性回归的预测结果误差很大，因此降水量与六项物理量之间无明显线性关系。

4 基于BP及RBF神经网络的降水量预测模型

4.1 BP神经网络

BP是一种为减小误差使网络的误差平方和最小［9］而通过梯度下降的学习方式反向传播来不断调整网络的权值和阈值从而达到目标参数的多隐含层层前馈网络［10］。

4.2 RBF神经网络

RBF神经网络是两层前馈网络，其隐藏层不是传统的神经网络层，隐层的功能是将输入向量的非线性可分离集转换为线性可分离集［11］。隐藏层的每一个神经元需计算输入数据到代表神经元聚类中心的距离，找到RBF作为激励函数的输入与聚类中心的距离r。第二层是一个简单的前馈层，网络输出由隐含层的输出结果经感知神经元或ADALINE线性加权输出［12］。最常用的径向基函数是高斯核函数，形式为

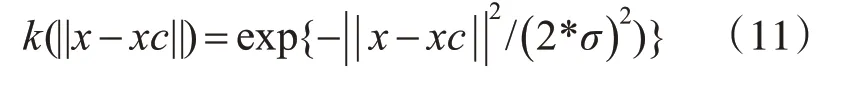
其中xc为核函数中心，σ为函数的宽度参数，控制了函数的径向作用范围。

xk为第k个输入样本，cj为第j个中心点，m为隐含层的结点数，n是输出的样本数［14］。可得到网络的输出为

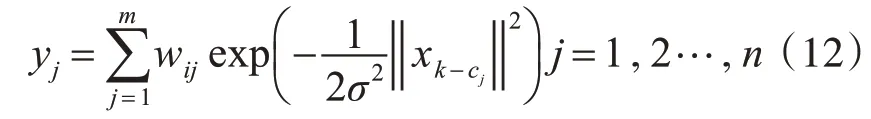
4.3 神经网络预测及结果分析

4.3.1 模型参数设置

BP神经网络在预测时为3层网络，其中输入层节点个数为自变量个数，隐含层节点数为9，隐含层函数tansig［13］，输出层函数purelin［14～15］，学习率设置为0.001，gaol为0.0001，最大迭代次数1000次。RBF神经网络在预测时隐含层节点数为30，隐含层为Gaussian核函数。

4.3.2 预测结果及评价

将6项物理量作为自BP，RBF经神经网络进行仿真预测，得到结果如图2～图3。

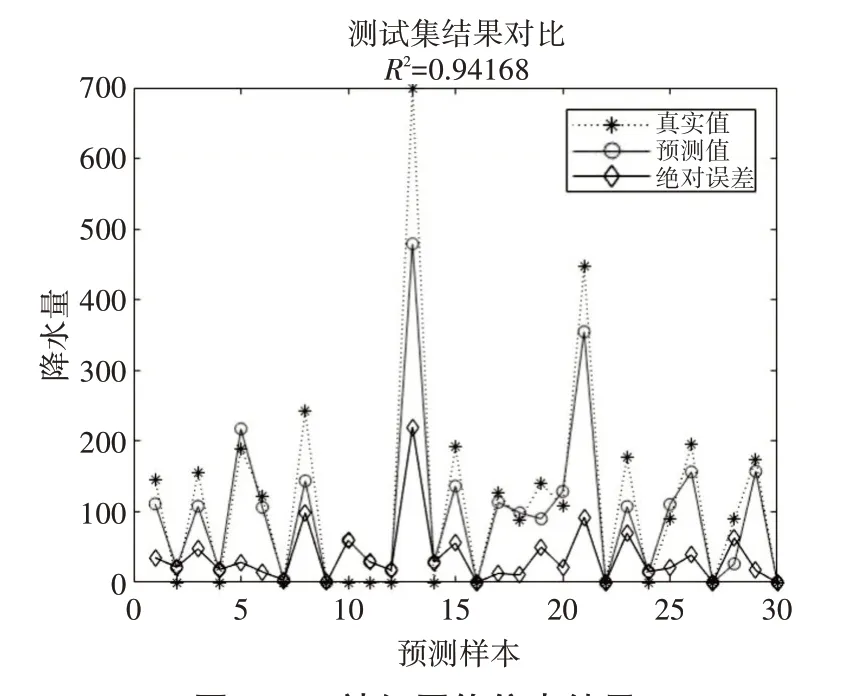
图2 BP神经网络仿真结果

图3 RBF神经网络仿真结果

BP和RBF神经网络的拟合优度都超过了90%，RBF的拟合优度高达99.8%绝对误差较小。采用MAE，MAPE，MSE，运行时间指标对两者进行评价对比，如表5所示。

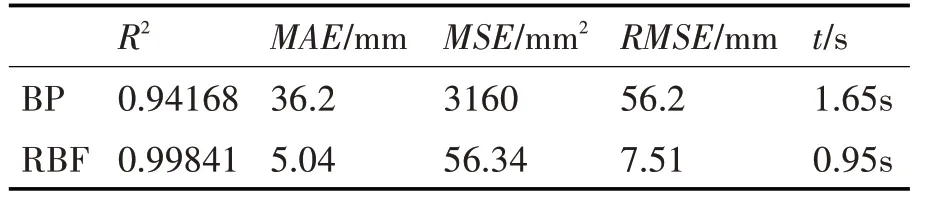
表5 仿真效果评价

从各项评价指标来看，RBF神经网络的误差明显小于BP神经网络，由于RBF局部逼近可以简化计算量所以其运行时间也较短，是理想降水量的预测模型。

4.3.3 最优模型的确定

为进一步验证将6项物理量作为输入的RBF神经网络模型是否为最优模型，本文利用6项物理量建立自变量随机选取的21个RBF神经网络仿真模型，运行得到的结果如图4～图8所示。

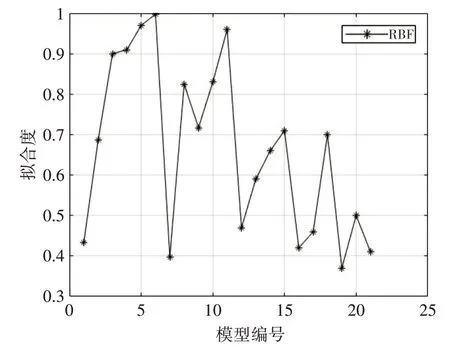
图4 21个模型的R2对比

图5 21个模型MAE对比

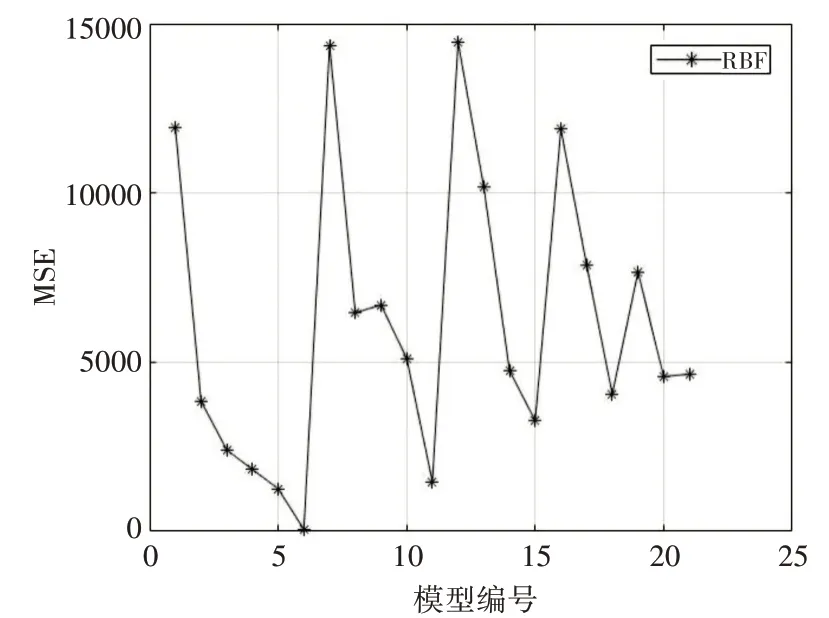
图6 21个模型MSE对比

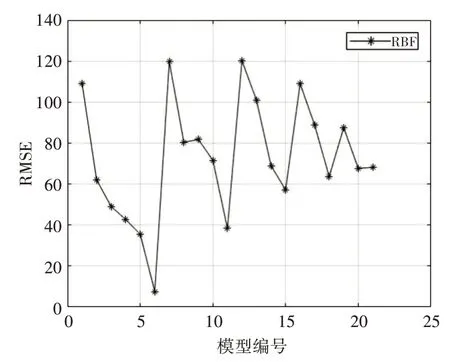
图7 21个模型RMSE对比

图8 21个模型运行时间对比

由上图可以看出随物理量参数的增加R2递增，MAE、MSE、RMSE误差减小，运行时间t的趋势不明显。

选取拟合度大于95%的模型做进一步比对得到表6。

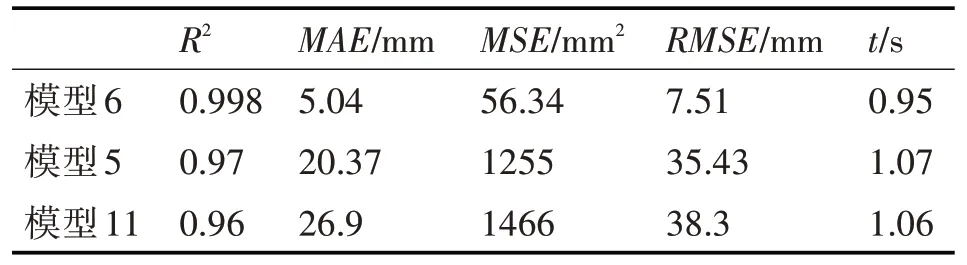
表6 R2大于95%的模型预测效果评价

模型6的所有指标均优于模型5和模型11，验证了将6项物理量作为自变量的RBF神经网络模型为最优模型，缺少任一变量都会导致信息的不完整性和准确度的缺失。同时也验证了4.2节中自变量选取的合理性和准确性。

5 结语

本文在理论和数据表现上对短时降水进行分析，分析了发生降水的三个物理条件及其对应的物理量。使用多元线性回归进行回归预测，发现其预测效果较差，物理量与降水量之间不存在明显的线性关系。使用非线性模型前馈神经网络BP，RBF进行预测，RBF表现出较高的准确性。最终，为选取最优模型建立了自变量随机选取的21个RBF模型并比较其预测结果，得到最优模型。本文提出的基于物理量选择和神经网络学习的短时降水量预测模型对短时降水量的预测在R2、MAE、MSE、RMSE、运行时间上都具有最优的预测精度。同时，短时降水量预测的复杂性还可以继续深入的研究，且本文的模型中BP和RBF的隐含层数设置为单层，可以考虑设置多层进行仿真或采用优化算法对模型进一步优化，以此降低模型的预测误差。