一种改进DBSCAN特征聚类的学习者类画像方法*

李 静 郝耀军 杨 瑜

（忻州师范学院计算机系 忻州 034000）

1 引言

随着信息化时代教育变革的深化，在线学习群体日益增长，面对海量的在线学习行为数据，如何从中挖掘学习者的群体学习特征，优化教师的信息化教学行为，已成为人们关注的热点问题。用户画像技术［1～2］的发展过程一直与互联网环境下的行为研究关系密切，因此利用用户画像进行用户信息或群体特征的挖掘是实现学习者类特征描述的一种有效解决方案。聚类分析是将没有分类标签的数据集，分为若干个簇的过程，是一种无监督的分类方法［3］，有效表达了类内的相似性与类间的排他性，在学习者群体特征描述方面得到了广泛应用。

近年来，在学习者群体聚类领域已出现了多种聚类算法，如基于划分、基于密度和基于层次的聚类等［4～6］。基于划分的聚类算法将距离作为相似性的度量指标，认为簇是由距离相近的对象组成，算法简捷高效，适合对大规模数据进行聚类［7］，但存在依赖初始聚类中心、对噪声样本点敏感、只能处理数值型数据等问题［8～10］。基于密度的聚类方法将各目标簇定义为基于密度可达关系的高密度相连样本的最大集合，可以识别任意形状的聚类簇［11］。但在面临密度不均匀的多密度数据集时，聚类质量较差。基于层次的聚类算法通过构建具有一定亲属关系的系统树图实现聚类，不需要确定初始簇数，可解释性好［12～13］。但聚类过程中各个步骤联系紧密，时间复杂度较高。之后，随着智能化技术的普遍应用涌现出一些智能聚类算法，如：人工神经网络聚类实现了层次化的非线性特征聚类［14～15］，基于深度学习的深度聚类算法实现了特征学习和聚类的联合优化［16～20］，从不同角度提升了聚类算法的性能，但该类算法适合处理大规模高维非结构化的数据，确定性先验信息的缺失是模型存在的问题。随着教育信息化进程的推进，学习空间多元化、学习时间多样化、学习环境无缝化等都为学习者的学习行为增加了更多不确定的因素，导致上述传统聚类算法在进行学习者群体划分时聚类质量会下降，传统的聚类算法面临新的挑战。

针对上述问题，本文提出了一种新的用于解决学习者类划分的S-DBSCAN聚类算法。经过充分分析学习者的行为特点，利用改进的PCA-GRBM算法提取学习者数据的多维特征，在此基础上采用基于密度的DBSCAN算法进行学习者群体特征聚类，并针对误判的噪声数据引入多重聚类的步骤，使其重新归入相应的簇，实现改进的S-DBSCAN聚类算法，以提高聚类质量。

2 改进的S-DBSCAN特征聚类算法

2.1 多维特征提取算法PCA-GRBM

为了使得原始的无标签数据集具有更明显的类别特征，本文提出了一种改进的PCA-GRBM多维特征提取算法。采用无监督学习的PCA算法降维提取线性特征；GRBM算法提取非线性特征，并将两种特征进行拼接，形成多维特征。这样既降低了线性特征的计算复杂度，又能充分利用神经网络的非线性逼近能力，最终实现对数据集类别特征的有效表达。多维度特征提取算法PCA-GRBM分为两个部分：PCA特征转换和GRBM特征学习，算法描述如下。

算法1基于PCA的线性特征转换

输入：学生学习行为数据集DataFrame（形如d ata={x1，x2，…，xm}）

1）数据预处理。对清洗后的各数据特征进行标准差标准化：X←(data-data.mean()/data.std())。

6）计算降维后的数据集，即转换得到的新特征。样本矩阵与投影矩阵相乘得降维后的数据集X1'=X·W。其中X为n×m，W为m×d′，d′＜m。

算法2基于GRBM的非线性特征学习

输入：学生学习行为数据集向量X（形如d ata={x0，x1，x2，…，xi}），可见层神经元个数i，隐藏层神经元个数j，学习率ε，训练周期N。

输出：学习到的新特征

1）数据预处理。对数据进行清洗及标准差标准化，假设初始训练数据集X～N(μ，σ2)。

2）模型初始化。可见层神经元中输入样本数据集X，即v0=x0，v1=x1，…，vi=xi；W，b随机赋为较小的值。

3）训练阶段。

f or j=0，1，2，…，j-1#根据式（1）获取隐藏层神经元的状态值

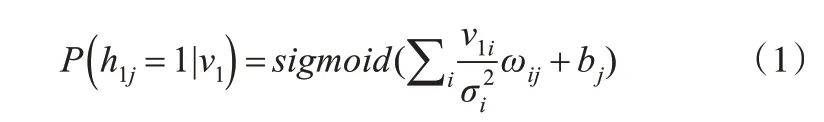
根据条件分布P(h1j|v1)采样h1j的二元数值；

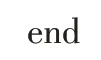
f or i=0，1，2，…，i-1#根据式（2）获取可见层神经元的状态值

其中，N(.|μ，σ2)表示均值为μ，方差为σ2的高斯概率密度函数。

根据条件分布P(v2i|h1)采样v2i的实值数据；

f or j=0，1，2，…，j-1#根据式（3）获取隐藏层神经元的状态值

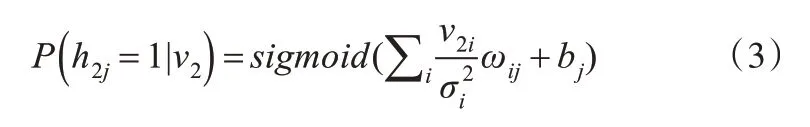
根据条件分布P(h2j|v2)采样h2j的二元数值；

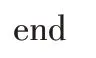
根据对比散度算法，按式（4）更新模型参数。

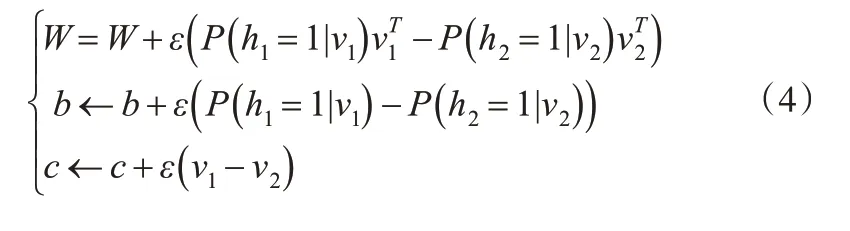
4）网络稳定后，隐层神经元的输出即为学习到的新特征X'2。

最后，将PCA算法提取到的线性特征与GRBM算法提取到的非线性特征进行横向拼接，得到数据集的多维特征

2.2 多重聚类算法S-DBSCAN

DBSCAN聚类算法把簇定义为由密度可达关系导出的最大密度相连的样本集合，可以识别任意数量和形状的簇，而且聚类过程可以发现噪声数据。但由于学习者数据存在多样性和个性化的特点，导致数据集的密度不均匀，传统的DBSCAN算法聚类得到的噪声数据较多。本文改进了传统的DBSCAN算法，提出一种S-DBSCAN多重聚类算法。首先使用DBSCAN算法初步生成聚类分组和噪声点，针对误判的噪声点，计算其与其他学习者多次章节测试答题情况的斯皮尔曼（spearman）相似度，并以此作为学习者间距离的衡量标准，进而将误判的噪声点重新进行划分，实现多重聚类，以提高聚类质量。S-DBSCAN多重聚类算法过程如下。

算法3S-DBSCAN多重聚类算法

其中，di分别为噪声点xi和xm的答题情况向量间的等级差。

7）将xi归入相似度最大样本所在的簇，得到新的簇划分C。

3 学习者类画像的构建

基于PCA-GRBM算法进行多维度特征提取后，使用改进的S-DBSCAN多重特征聚类算法实现学习者类画像的构建，具体步骤如图1所示。

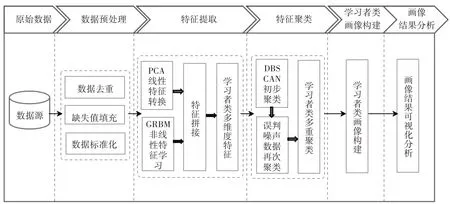
图1 学习者类画像构建流程

1）对采集到的学习者数据进行预处理，存储于CSV文件中，用于特征提取、聚类以及学习者类画像的构建。

2）对文件中的学习者数据使用PCA算法提取线性特征，使用GRBM算法提取非线性特征，将提取到的两种特征进行拼接，生成多维特征矩阵。

3）在特征聚类阶段，将步骤2）生成的多维特征矩阵输入DBSCAN算法中，初步生成聚类分组，提取噪声数据，并删除真实噪声点。

4）计算误判的噪声数据与其余样本点多次章节测试结果的答题相似度，并将噪声数据归入与其相似度最大的样本点所在的簇，形成新的聚类簇。

5）依据改进的S-DBSCAN多重聚类算法构建学习者类，分析各类型学习者的特点，并进行画像结果的可视化输出。

4 实验与结果分析

4.1 实验环境和数据源

本文采用Python 3.7作为实验平台，操作系统为Windows 10，CPU为CoreTM i7-9750H。实验数据来源于超星学习通平台，共收集到《计算机专业英语》课程两年四个学期322名同学的线上学习数据，分为学生基本属性数据和学习行为数据两部分。其中，基本属性数据包括学号、入学年份与性别。学习行为数据包括任务点完成比例、课程视频进度、观看视频的平均反刍比、章节测试进度、任务点完成数、视频观看时长、参与讨论次数、章节学习次数、章节测试平均成绩、综合成绩及成绩等级。

4.2 PCA-GRBM多维特征提取

1）基于PCA的线性特征转换

结合采集到的学习者数据，计算各特征维度的累积贡献率可知，8个主成分即可表达原始数据98%以上的信息，故提取转换后的8个特征作为数据集的线性特征，累积分布图如图2所示。

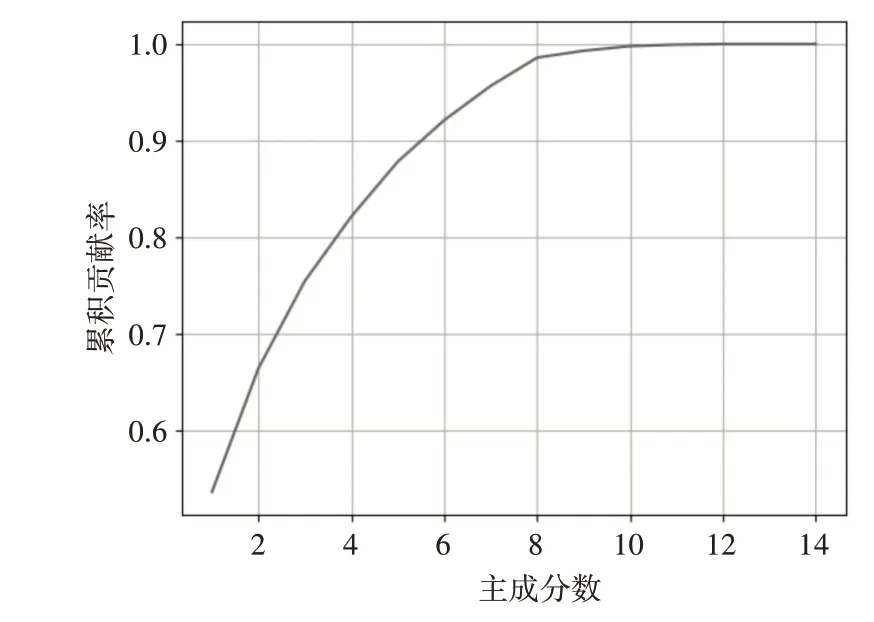
图2 PCA特征累积分布图

2）基于GRBM的非线性特征学习

经多次实验比较，本文选用含20个隐层神经元的高斯-伯努利受限玻尔兹曼机进行特征学习，学习率为0.1，经30次迭代，网络收敛，均方误差为12.37，网络训练过程如图3所示。

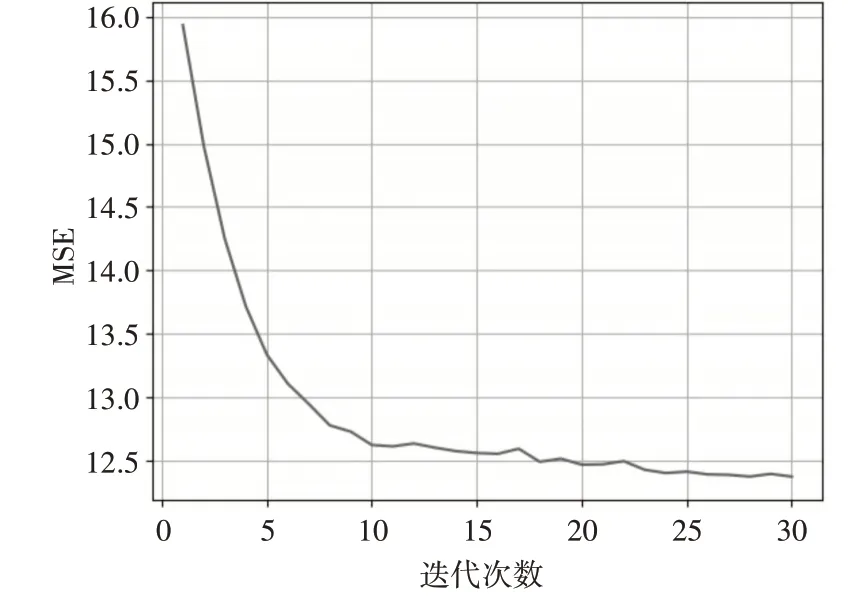
图3 GRBM网络训练过程

记录网络输出结果，得到GRBM学习到的20个新特征，与PCA转换得到的8个线性特征进行拼接，产生多维特征提取后的322×28特征矩阵。绘制原始数据与PCA-GRBM算法多维特征提取后数据的三维散点图如下所示。

可以看出，由于学习者学习行为多样性和个性化的特点，原始数据集的类别特征并不明显，当进行多维特征提取后，有了较为明显的类别特征。同时，基于原始数据分布特点，很难确定初始聚类中心，不适合采用基于划分的聚类算法，故本文采用基于密度的聚类算法DBSCAN。

4.3 S-DBSCAN多重特征聚类

基于经典的DBSCAN聚类算法，对多维特征提取后的学习者数据进行初步聚类，Eps邻域半径为2，核心点阈值为5，得到4个聚类簇及噪声数据（紫色点），如图4（b）所示。由图可知，DBSCAN算法聚类后，得到的噪声数据较多，其中很大一部分是误判噪声。故本文提出在初步聚类后，再次进行聚类操作，将真实噪声点删除，计算误判噪声点与其它学习者在24次章节测试答题中的斯皮尔曼相关系数，作为相似性度量的依据，将误判噪声数据重新划归到与其相似度最高的样本所在的簇，实现特征的多重聚类。S-DBSCAN算法进行多重聚类后的结果如图5所示。

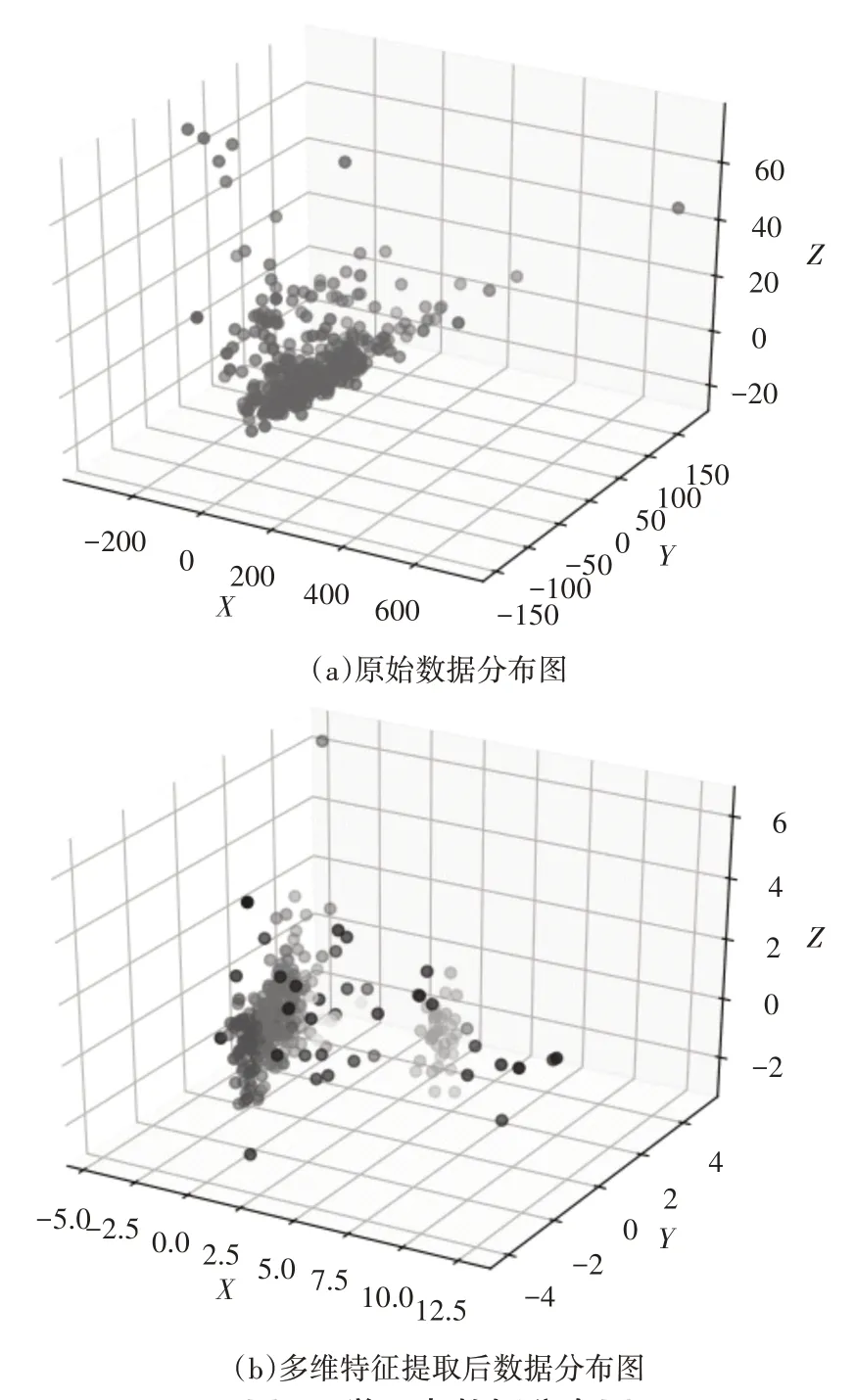
图4 学习者数据分布图

图5 S-DBSCAN聚类结果

4.4 算法性能比较

为验证算法的性能，本文在采集到的学习者数据集上进行了4组实验，分别是进行多维特征提取前直接使用DBSCAN算法进行聚类的基线模型；进行多维特征提取后，使用Kmeans，DBSCNA及改进的S-DBSCAN算法进行聚类的后三种模型。在聚类簇数为4时，对比各种模型的DBI指数，实验结果如表1所示。

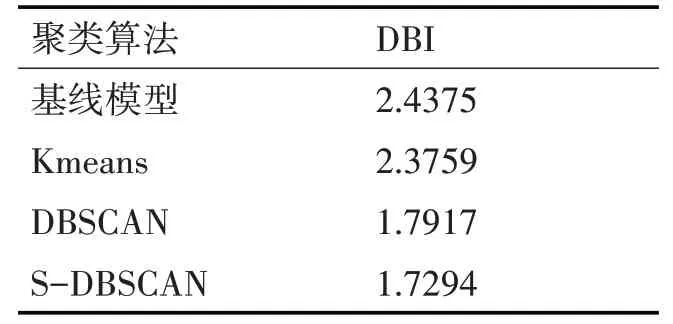
表1 不同聚类算法DBI指数比较

戴维森堡丁指数（DBI）是评估聚类算法优劣的一个重要指标，是指簇内所有点到该簇质心点的平均距离之和与两个簇质心间距离比值的最大值。DBI值越小，表示类内距离越小，类间距离越大，聚类效果越好。从表1可以看出，特征提取前的基线模型DBI指数最大，聚类效果较差。进行多维特征提取后，三种模型的DBI指数都有所减小，说明PCA-GRBM特征提取算法有效。由于学习者行为的个性化与多样性特点，基于密度的DBSCAN算法比基于划分的Kmeans算法DBI指数减小了24.6%。而改进的S-DBSCAN算法在经典DBSCAN聚类的基础上，使用相似性度量进行了多重聚类，DBI指数比DBSCAN算法减小了3.5%，实验取得了较好的效果。

4.5 学习者类画像分析

依据改进S-DBSCAN算法产生的聚类结果，在数据集上构建4个学习者类，每类学习者人数统计如图6所示。在任务点完成率、观看视频进度、观看视频平均反刍比等八个特征上各学习者类的学习行为平均分布情况如图7所示。

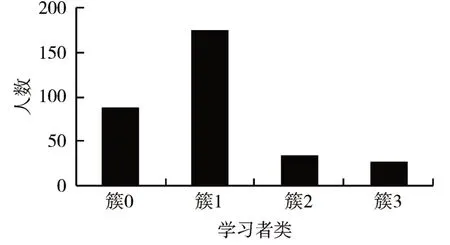
图6 各学习者类人数统计

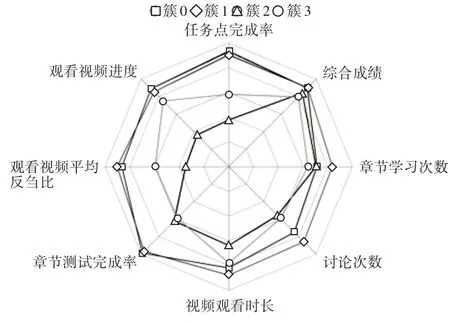
图7 各学习者类学习行为平均分布情况

可以发现，簇1学习者类具有最大的学习者比例，占学习者总数的54%。该类学习者在任务点完成、视频观看进度、章节测试完成方面表现较好，但完成率并不是最高。观看视频反刍比最高，说明在反复观看知识重难点。参与线上讨论次数最高，说明学习具有积极性和主动性，最终综合成绩是最高的，此类学习者可定义为高效学习者。

簇0学习者类在任务点完成、视频观看进度及章节测试完成方面表现是最好的，章节测试平均成绩也最高。反映出该类学习者在课程学习上花费时间较多，具有扎实的基础知识。但视频观看反刍比及参与讨论次数略低于簇1类学习者，体现其积极思考及主动学习能力欠缺，所以综合成绩也低于簇1类学习者，将此类学习者定义为优秀学习者。

簇2学习者类各项内容完成情况最低，但偏好进行章节测试，测试成绩也较高，考虑到章节测试成绩会作为课程平时成绩的一部分，该类学习者在成绩驱动下进行学习，不能充分发挥主观能动性，未能很好地掌握知识点并学以致用，将此类学习者定义为低水平学习者。

簇3学习者类各项任务完成率并不是最低的，但章节测试完成情况最差，测试平均分最低，综合成绩最低。该类学习者在学习过程中存在困难，缺乏针对性练习，是教学过程应重点关注的人群，将其定义为高风险学习者。

5 结语

本文对基于改进S-DBSCAN聚类算法的学习者类画像方法进行了深入的探讨，研究了如何在PCA-GRBM算法提取多维特征的基础上，使用S-DBSCAN算法进行多重聚类，并将其应用于学习者类构建中。在学习者数据集上实现了准确的群体划分，改善了聚类算法的性能。实验结果表明，提出的多维特征提取算法更精准地发掘了数据集的类别特征。而多重聚类算法能充分利用同类学习者间的答题相似性，提高聚类的准确性。相对于经典的DBSCAN聚类算法，DBI指数最低，获得了很好的性能，充分体现了改进算法在学习者类别描述过程中的有效性。