基于改进层次分析法的企业金融风险分析模型*

谢亚妮

（榆林学院管理学院 榆林 719000）

1 引言

企业在从事各类金融活动时，所发生的利率、汇率以及商品价格等方面的损失均称为金融风险，但是不同原因导致的损失结果存在差异，其风险程度则存在差异。企业在运营管理过程中，准确分析风险类型，对于降低金融损失具备重要意义［1～2］。层次分析法作为一种决策方法，以要实现的总目标为依据，将其实行分解处理形成数个目标后，依据各个因素之间的关联［3］，构成多层次的分析结构模型，依据相应的定量和定性方法，获取以最高层为参照的权值结果以及总目标的综合权重，确定最佳方法，实现多目标的综合分析和评价。当下，如何准确分析企业金融风险，已经成为学术界众多学者关注研究的问题。陈振龙［4］等和张冰洁［5］等针对金融风险的分析，分别以藤Copula分组模型、CoES模型为基础，度量金融风险水平，展开相关分析，分别依据企业资产之间的关联性和损失均值的度量结果，分析企业风险水平。上述方法在度量分析过程中，对于权重指标的分析和确定存在一定欠缺，风险指标之间的关联性无法清晰、准确体现。存在分析结果的片面性［6］。基于此，本文以层次分析法的风险指标权值确定为基础，采用灰色关联对其实行改进，确定指标间的关联性，避免层次分析法的局限性，保证风险指标权重的客观性，实现企业金融风险的可靠分析。

2 改进层次分析法的企业金融风险分析模型

2.1 企业金融风险指标体系构建

企业金融风险分析时，需量化分析对企业金融风险造成影响的因素，即风险指标体系的构建。本文采用层次分析法建立企业金融风险分析指标体系，指标体系包含一级指标、二级指标，将上述指标用于企业金融风险分析。指标详情见表1。

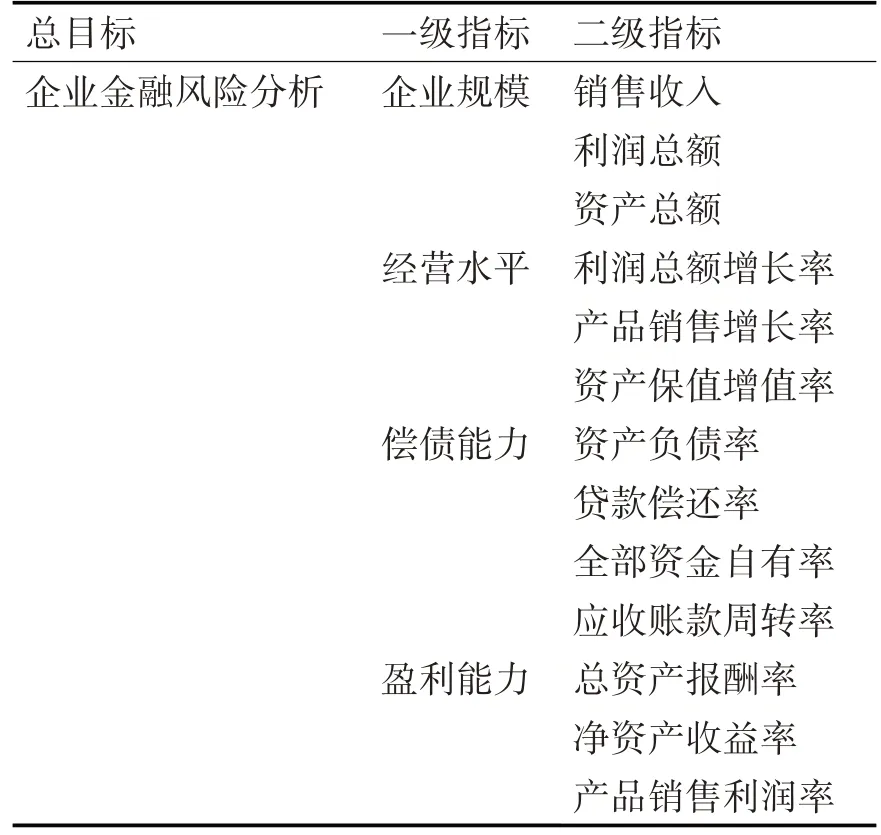
表1 企业金融风险指标体系

2.2 风险指标的模糊化处理

X=｛x1，x2，x3，x4｝表示企业风险分析论域，其中x1、x2、x3、x4分别表示四个一级风险指标，以分析对象来说，每一个风险指标对分析结果的贡献均存在差异［7～8］，为实现指标的定量分析，需对其实行模糊化处理，处理采用隶属度函数完成，保证样本数据处于［0，1］范围内。设置企业的信用等级用j表示，且j=1，2，3，4，分为4个等级，分别表示不信任、较低信任、一般信任和完全信任，见表2。

表2 等级详情

信用等级集合为：Y=｛y1，y2，y3，y4｝，其中包含的元素分别对应4个等级；x1、x2、x3、x4的6个界限值为：ki=（i=1，2，3，4，5，6），则隶属度函数的定义为

以上三个公式分别是j=1、j=2，3、以及j=4的条件下的隶属度函数。

2.3 基于改进的层次分析法的指标权重确定

风险指标确定后，需确定指标的权重，为保证权重结果的客观性［9］，本文将灰色关联模型和层次分析法相结合，改进层次分析法，以此完成所有风险因素的整体对比机制［10］，并且通过灰色关联系数矩阵确定各个专家对于风险总贡献度的认知结果，结合灰色关联和层次分析法的优势，完成企业金融风险分析［11］。其详细步骤如下所述：

1）m表示数量，包含专家和待分析序列，分析因素数量用n表示，对风险因素实行打分和处理，分别为层次和总体，处理标度为（0，1），该值大小决定风险程度；前者越大后者风险越小［12］。X0（k）表示标准参考序列，其为总体风险因素，为获取待分析矩阵Xi（k），以列的方式将待分析风险实行排列得出，且i=1，2，…，m，k=1，2，…，n。

2）对排列后的Xi（k）和X0（k）进行处理，得到：

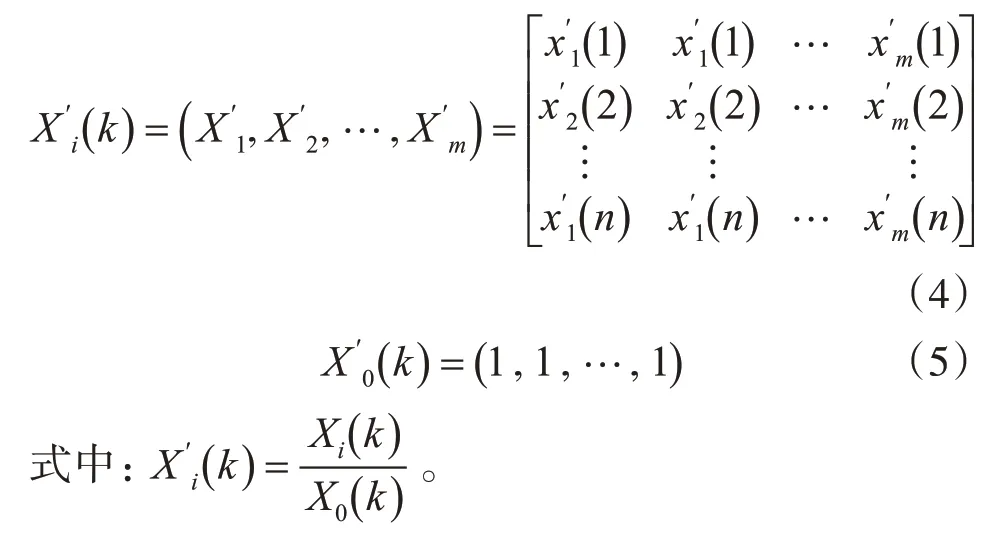
3）为获取绝对差矩阵，采用绝对差，对初值化后的矩阵实行运算［13］，则得出：

式中：分辨系数用ζ表示，其取值最佳时，可控制分析结果的准确性，同时提高区分能力，仅为ri（k）；M、m表示最大、最小元素，属于Δi(k)。对式（7）实行关联运算后，获取ri（k）矩阵。

5）为获取互反判断矩阵，对ri（k）实行拆分处理，将其内各个元素实行倍数增加，均为10倍，取整数结果，形成新矩阵以列的顺序提取矩阵中的专家评分结果，使其形成纵横对比形式，仅为风险因素；分别以行、列各自为参照元素［14］，相互对比获取两者差值，如果比较元素小于参照，差值结果加1。按照该处理方式，依据获取顺序，将获取的结果组成互反矩阵，即为灰色关联判断矩阵Ai。

6）对Ai分别实行方根运算，并以上级风险为参照，获取风险因素对其的影响权重［15］：

7）一致性检验：计算Ai特征值［16］，具体为

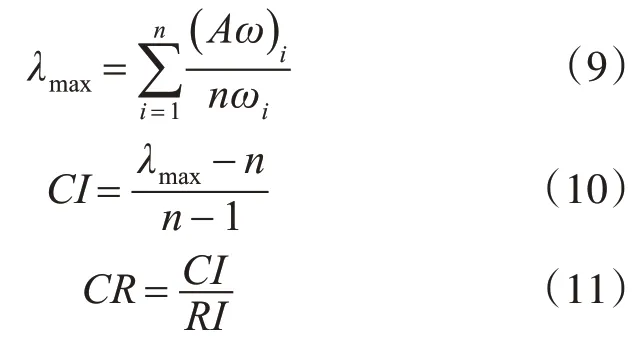
式中：C I、RI均表示一致性指标，后者为随机；λmax表示特征值；C R表示一致性比率，依据该值结果判断Ai是否符合一致性，其值小于0.1，表示符合，反之不符合。当其不符合时，为不影响风险分析结果，将其删除；最后依据专家分析结果，确定每一个风险因素的权重，且以上级总风险为参照。

2.4 模糊综合评价模型

依据Y=｛y1，y2，y3，y4｝等级完成各个风险指标的评价，对其实行量化后，建立模糊关系矩阵R：

式中：rij表示隶属度，属于模糊子集，且在以xi为参照的情况下，yi的分析结果。

将获取的权重向量集合和R权重向量集合ω={ω1，ω2，…，ωm}组合，得出：

3 实验结果与分析

为验证本文方法对于企业金融风险分析的应用效果，选取国内某知名生产企业连续5年内的实际财务数据作为测试使用数据。本文方法分析指标结果见表3，偿债能力是对流动比率和速动比率实行拟合后获取的数据。

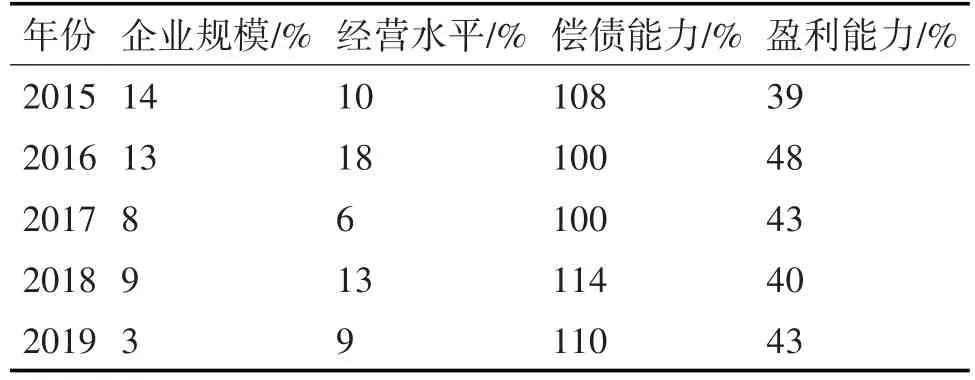
表3 指标数据结果

分析本文方法指标选取的准确性，对于分析结果存在直接影响，本文采用差异度作为衡量本指标，测试本文选取指标和基准指标间的差异度，结果见图1。依据图1测试结果可知：本文选取指标与基准指标吻合程度较高，因此，采用文本方法确定的指标可用于准确完成企业金融风险分析。

图1 指标的差异度测试结果

由于每一个风险指标对分析结果的贡献均存在差异，即不平衡现象，为实现指标的定量分析，需对其实行模糊化处理。因此，测试本文方法对指标的模糊化处理效果，采用F1-measure（加权调和平均值，为查准率和召回率）、G-mean（几何平均值，为召回率和特异度）两种指标作为衡量标准，分析本文方法的处理结果，见图2。两者值越接近1表示模糊化效果越好。依据图2测试结果可知：本文方法在对不同年份中的风险指标实行模糊化处理的F1-measure和G-mean结果均在0.8以上，表明本文方法可有效处理风险指标对分析结果的贡献均存在差异，即不平衡现象。

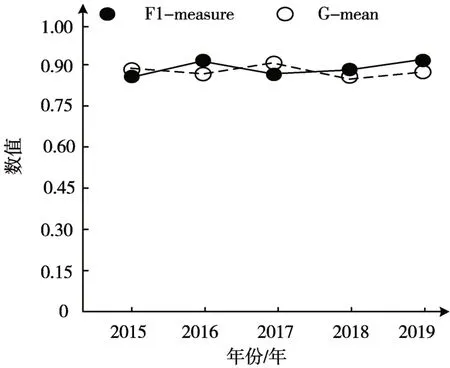
图2 模糊化效果测试

分辨系数ζ值对于准确率和关联系数的区分结果存在直接影响，因此，测试在其不同取值下的分析结果的准确率以及有效区分结果，见图3。从图3可知：ζ取值不同，其随着指标间关联系数的关联程度增加，呈现不同变化，ζ=0.4时，本文方法分析结果的准确性呈现下降趋势；取值为0.6时，本文方法分析准确率呈现上升趋势；取值为0.5。时，则分析准确率平稳在0.90上下；除此之外，关联程度高于50%以后，关联系数的有效区分结果中，取值为0.5时，最高区分比例高于0.95，虽然在关联程度低于50%以内时，区分比例在0.5左右，但是，结合实际运算过程中，指标间的关联程度在模糊化处理后，关联程度高于50%，因此，本文方法ζ=0.5。

图3 分辨系数测试结果

依据文中创建的指标体系，采用本文方法获取判断矩阵后，计算一级指标的权重结果，并获取模糊关系矩阵，两者结合后，计算实验某知名生产企业金融风险评估结果为B=（0，0.39，0.52，0.40），依据最大隶属度原则，确定B的最大分量为0.52，即为企业的风险对应等级为Y4，表示该企业的信用等级为完全信赖。依据该信用结果，对该企业5年内的交易分布结果实行统计，结果为5年的平均结果，见图4。依据图4测试结果可知：该企业83.5%的交易均分布在完全信赖的信用等级中，一般信赖的交易比例为12.6%，信赖较低的交易比例为3.2%，不信赖的交易分布仅占0.7%。该结果体现本文方法可有效完成企业的金融风险分析，并且可为企业交易分布的风险统计提供可靠依据，保证企业掌握自身交易分布情况，针对交易风险采取应对措施。

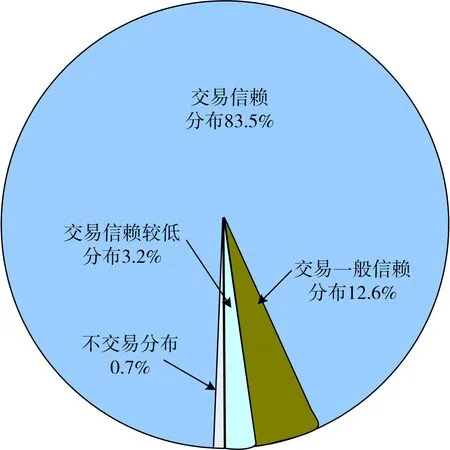
图4 企业交易分布情况

4 结语

企业的金融状态，决定企业的发展和正常运营，因此，为保证企业的良性运转，需及时掌握企业的金融风险状况。本文研究基于改进层次分析法的企业金融风险分析模型，对企业运行中的金融风险实行定量以及定性分析，判断企业的信用等级。并通过相关测试表明：本文方法选取的风险指标的准确率较高，可用于表示企业的金融风险；可良好地处理金融风险指标中不平衡数据，保证企业的金融风险结果可靠性，并可依据分析结果统计企业的交易分布情况，有助于企业的金融管理。