例谈“不等式”中“结构模式”的建构和应用

广东 周佳鑫

2021年举行的深圳市调研考中，大多数学生都认为试卷总体难度适中.不过有些题目给人一种似曾相识，却又无从下手的感觉，比如试卷中第11题.相比之下，学生对考查同样知识点的第8题显得更加有把握.这种情况反映出了对于相同的知识点，不同的考查方式，学生的表现会呈现较大差异.那么在日常教学中，广大教师应该从哪些渠道入手，缩小这种差异呢？对此，笔者对比研究了上述两道试题，并与备课组的老师们进行沟通交流，反思日常教学中需要注意的问题.

【例1】(2021·深圳调研考·8)已知实数a,b,c满足a>b>0>c，则下列不等式中成立的是

( )

答案:B

( )

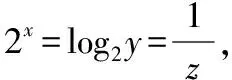
A.y=z>xB.z=x>y

C.y>z>xD.z>y>x

答案:ACD

我们在教学中更多强调的是对数学概念的理解，对定理、公式的推导，对经典题型的训练，而忽视如何从问题出发抽象概括建立数学模型，通过对模型的分析研究去认识和解决问题.笔者试图以此为起点，研究和探索高中阶段人教版《2019版高中数学教材必修一(A)》(以下简称《新教材》)中二次函数与一元二次方程、不等式教学中的“结构模式”.

1.问题的分析与解决

高中阶段的不等式教学着重于大小的比较，考查形式大致可以分为两类，即恒成立问题和存在性问题.从这个分类的层面出发，不难看出例1属于恒成立问题，而例2属于存在性问题.对于不等式的相关试题，绝大多数学生在考场上首选的解题思路是利用特殊值进行检验.由于反例只能进行否定，而无法作为证明，所以特殊值法在使用上具有较大的不稳定性，在一定程度提高了不等式问题的难度.此外，不等式将实数的比较大小抽象成符号间的比较，也让不少学生望而却步.

1.1 回归教材，夯实“不等式”教与学的基础

不等式作为数学的重要组成部分，学习不等式相关结论的最好方法是经历数学推导过程，从过程中总结方法、经验，构建知识结构体系.《新教材》在内容安排上按照“现实情境→总结归纳→研究性质→应用性质”的顺序开展.这种顺序有助于学生了解知识的来龙去脉，理解数学的本质，形成对数学知识的联系性和整体性的认识，体会不等关系和不等式的意义和价值.基于此，笔者认为在教学中应该重视在解决具体问题的教学活动中突出数学的一般方法，以活动为载体，以核心问题和关键知识为主线，以章节知识的基本结构为蓝图，为学生构建完善的知识方法体系和认知结构，搭建起切实可用的“脚手架”.通过教学活动，帮助学生系统地认识和理解相关知识和结构，进而达成知识方法和结构的协调统一，为后续的学习奠定基础.

二次函数与一元二次方程、不等式章节知识结构图

在教学过程中，教师可以合理地使用化归与转化思想，引导学生将陌生的问题情境转化为熟悉的结构，进一步完善认知结构.

“不等式”这章要求学生掌握用不等式刻画不等关系，学会利用不等式的性质解决不等式问题.在此基础上，借助不等式的性质研究基本不等式，利用基本不等式解决相应的最值问题.每条不等式性质都可以从不同的角度来认识，教师在教学活动中应该加以选择，使相关结论和性质构建联系.

通过上述认知结构的构建和“复习”后，学生就可以较为轻松地解决例2了.

1.2 以不等式性质为抓手，选择合适的求解模式

对于同一道题来说，往往有不同的切入点，从而引申出不同的解法.一题多解可以有效地梳理知识间的脉络，完善学生的认知结构，夯实基础，提升解题能力.

1.2.1 从函数思想的观点出发，运用数形结合解决问题

对于例2，多数学生的第一个想法是将实数x,y,z具体计算出来.然而，题干中给出的方程属于超越方程，这导致了该想法的夭折.如果学生在平时的学习中有从代数、几何、函数等不同角度研究不等式的经验，那么就可以自然地联想到数形结合法，将不等式的问题和函数图象联系起来，从而将问题解决.

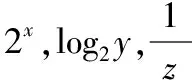
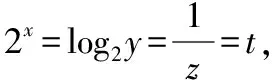
数形结合是解答数学问题的常用解题模式，对于不等式问题也具有较好的效果.

1.2.2 从求解的方法出发，采用适当的方法解决问题

分析法、综合法、倒推法、特殊值法都是适用于解答不等式问题的一般方法，例2作为一道客观题，可以从结论出发，结合倒推法和特殊值法将其解决.

倒推法和特殊值法在本题中的作用其实是排除，排除法是求解数学问题的一种常用解题模式，适用于选择题.

1.2.3 从类题的基础解法出发，利用比较法解决问题

本题的选项本质是比较大小，而比较法是此类问题的常用解法.结合题干的条件，可以采取作差法求解.

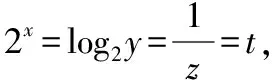
比较法是研究不等关系的重要基础手段，脱胎于实数大小的比较，是一种常见的解题模式.解法4在使用时对比较法做了一定程度的调整，使其应用更加灵活，不仅适用于恒成立问题，也可以解决存在性问题.

值得注意的是，例2如果将题干中的每两项进行对比的话，容易得出必有y>x，且x与z、y与z之间没有确定的大小关系，因而除了选项B之外，其余三个选项都可能成立，从而实现快速解决本题的目标.

2.结束语