注重融会贯通 聚焦核心素养——数列综合问题分析

江苏 杨 鑫 张启兆

高考要求学生能够触类旁通、融会贯通，既包括同一层面、横向的交互融合，也包括不同层面之间、纵向的融会贯通.

数列作为高中数学的重要内容，与高中数学的其他分支有着密切的联系，如数列与函数、不等式、数列和概率等，总是能够建立千丝万缕的联系.

从思想方法上来看，数列将计算、推理、猜想、归纳融于一体，具有很强的灵活性与综合性，代数的美在数列中得到了淋漓尽致的体现.

从高考来看，数列作为高考的必考内容，能全面考查学生的数学抽象、逻辑推理、数学建模、数学运算、直观想象等数学核心素养.一些数列综合问题则更为全面地考查学生数学推理能力和分析问题、解决问题的能力.本文以近几年高考(或模考)中的典型问题为例，剖析数列综合问题的热点题型及求解策略.

1.数列与函数、方程交汇的综合问题

数列是定义域为正整数集的特殊函数，这就意味着一些函数知识可以用于解答相关的数列问题，包括函数图象、函数性质、导数相关知识等，都能用于分析数列综合问题．为了更好地掌握该类题型的解题思路，应提高函数知识的应用意识，能灵活运用数列通项公式、前n项和等知识解题．另外，在进行推理时应时刻关注数列的自变量n，保证得出的结论有意义，必要情况下可进行分类讨论．

【例1】2021年是充满挑战和机遇的一年.疫情再次反复，给世界带来了巨大的冲击与改变，也在客观上使得人们更加重视科技的力量和潜能.某公司一下属企业从事某种高科技产品的生产.假设该企业第一年年初有资金5 000万元，并将其全部投入生产，到当年年底资金增长了50%，预计以后每年资金年增长率与第一年相同.公司要求企业从第一年开始，每年年底上缴资金t(t≤2 500)万元，并将剩余资金全部投入到下一年生产.设第n年年底企业上缴资金后的剩余资金为an万元.

(Ⅰ)判断{an-2t}是否为等比数列？并说明理由；

(Ⅱ)若企业每年年底上缴资金t=1 500万元，第m(m∈N*)年年底企业的剩余资金超过21 000万元，求m的最小值.(lg2≈0.301 0;lg3≈0.477 1)

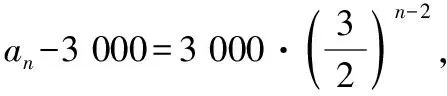
所以m-2≥5，m≥7，

因此m的最小值为7.

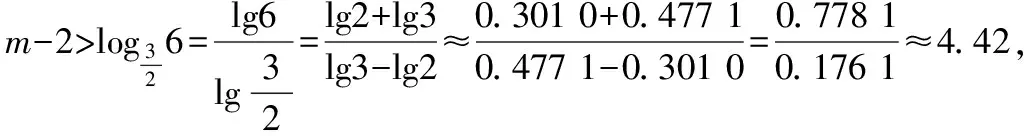
m≥7，因此m的最小值为7.

教学启示：在教学中，要引导学生认真审题，抓住关键词，分析探究出关键点，培养学生在审题中认真观察、分析、归纳、联想的能力，形成顽强、积极、求异创新的人格.这对突破解题思维障碍，提高解题能力大有裨益.求解本题时还要引导学生认识到：

(1)数列是一类特殊的函数，它的图象是一群孤立的点；

(2)转化以函数为背景的条件时，应该注意题中的限制条件，如函数的定义域，这往往是很容易被忽视的问题；

(3)利用函数的方法研究数列中的相关问题时，应准确构造相应的函数，注意数列中相关限制条件的转化.

(Ⅰ)证明：数列{bn}是等差数列;

(Ⅱ)求{an}的通项公式．

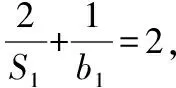
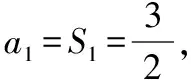
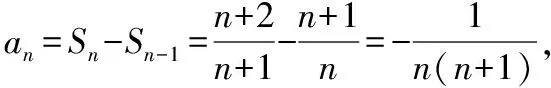
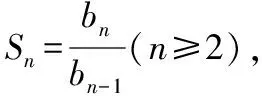
2.数列与不等式交汇的综合问题

数列与不等式结合的综合题通常与数列的前n项和结合设问，因此，求解时可灵活应用数列前n项和求解方法，包括公式法求和、分组求和、裂项求和、错位相减法求和等.然后使用基本不等式、函数单调性或放缩法等找到与目标之间的联系.同时，要记忆一些常见的放缩技巧并不断地训练，直至正确牢固地掌握.

【例2】(2021·天津卷·19)已知{an}是公差为2的等差数列，其前8项和为64．{bn}是公比大于0的等比数列，b1=4,b3-b2=48．

(Ⅰ)求{an}和{bn}的通项公式；

【解析】(Ⅰ)因为数列{an}是公差为2的等差数列，其前8项和为64，

所以an=1+2(n-1)=2n-1,n∈N*.

设等比数列{bn}的公比为q(q>0)，

所以b3-b2=b1q2-b1q=4(q2-q)=48，解得q=4或q=-3(舍)，

所以bn=b1qn-1=4n,n∈N*.

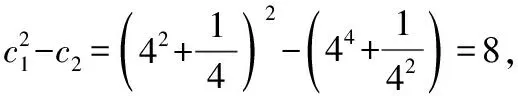
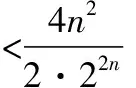
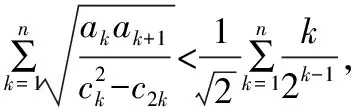
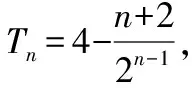
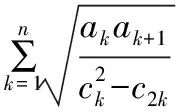
(Ⅰ)求{an}和{bn}的通项公式；

【解析】因为{an}是首项为1的等比数列且a1，3a2，9a3成等差数列，

所以6a2=a1+9a3，所以6a1q=a1+9a1q2，

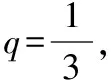
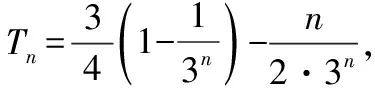
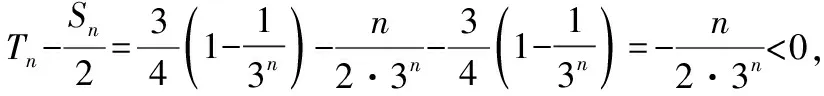
教学启示：解题后教师可引导学生对题进行变式拓展，让学生经历提出问题、分析问题、解决问题的再创造，这不仅仅是知识的再创造，也是问题的再创造，更是解题方法的再创造，而这样的过程能使学生的学习达到触类旁通的效果.如果学生解题后未进行反思、回顾和拓展，将会导致获得的知识系统性减弱、结构性变差.因此解题后的反思是非常必要的，能使学生从更高的观点、用更宽的视野、更理性的眼光去思考数学问题，领悟数学哲理.上述解法告诉我们，不等式问题的处理方式灵活多变，本题所用的作差法是证明不等式的通性通法，激发了学生学习数学的兴趣.

3.新定义型数列的综合问题

数列新定义题是各级各类考试的热点之一，解题的关键在于深入理解新定义，充分挖掘隐含条件，灵活运用所学数列知识.在解题过程中要灵活运用题干已知条件，把握本质，实现数列各项关系的灵活推导与转化.

【例3】(2021·北京卷·21)定义Rp数列{an}：对p∈R，满足：①a1+p≥0，a2+p=0；②∀n∈N*,a4n-1

(Ⅰ)对前4项2，-2，0，1的数列，可以是R2数列吗？说明理由；

(Ⅱ)若{an}是R0数列，求a5的值；

(Ⅲ)是否存在p∈R，使得存在Rp数列{an}，对任意n∈N*,Sn≥S10？若存在，求出所有这样的p；若不存在，说明理由．

提示：(Ⅰ)由题意考虑a3的值即可说明数列不是R2数列；

(Ⅱ)由题意首先确定数列的前4项，然后讨论计算即可确定a5的值；

(Ⅲ)构造数列bn=an+p，易知数列{bn}是R0的，结合(Ⅱ)中的结论求解不等式即可确定满足题意的实数p的值.

【解析】(Ⅰ)由性质③结合题意可知0=a3∈{a1+a2+2,a1+a2+2+1}={2,3}，

矛盾，故前4项2,-2,0,1的数列，不可能是R2数列.

(Ⅱ)性质①a1≥0,a2=0，

由性质③am+2∈{am,am+1}，因此a3=a1或a3=a1+1，a4=0或a4=1，

若a4=0，由性质②可知a3

若a4=1,a3=a1+1，由a3

因此只能是a4=1,a3=a1.

不满足a2=0，舍去.

当a1=0，则{an}前四项为0，0，0，1.

下面用数学归纳法证明a4n+i=n(i=1,2,3),a4n+4=n+1(n∈N)：

(ⅰ)当n=0时，经验证命题成立；

(ⅱ)假设当n≤k(k≥0)时命题成立，当n=k+1时,

若i=1，则a4(k+1)+1=a4k+5=aj+(4k+5-j)，利用性质③,

{aj+a4k+5-j∣j∈N*,1≤j≤4k+4}={k,k+1}，此时可得a4k+5=k+1；

否则，若a4k+5=k，取k=0可得a5=0，

而由性质②可得a5=a1+a4∈{1,2}，与a5=0矛盾.

同理可得

{aj+a4k+6-j∣j∈N*,1≤j≤4k+5}={k,k+1}，有a4k+6=k+1；

{aj+a4k+8-j∣j∈N*,2≤j≤4k+6}={k+1,k+2}，有a4k+8=k+2；

{aj+a4k+7-j∣j∈N*,1≤j≤4k+6}={k+1}，又因为a4k+7

即当n=k+1时命题成立，证毕.

综上可得a5=a4×1+1=1.

(Ⅲ)令bn=an+p，由性质③可知，

∀m,n∈N*,bm+n=am+n+p∈{am+p+an+p,am+p+an+p+1}={bm+bn,bm+bn+1}，

由于b1=a1+p≥0,b2=a2+p=0,b4n-1=a4n-1+p

因此数列{bn}为R0数列.

由(Ⅱ)可知,

若∀n∈N*,a4n+i=n-p(i=1,2,3),a4n+4=n+1-p；

S11-S10=a11=a4×2+3=2-p≥0，S9-S10=-a10=-a4×2+2=-(2-p)≥0，

因此p=2，此时a1,a2,…,a10≤0，aj≥0(j≥11)，满足题意.

教学启示：新定义型数列综合题以数列为载体，主要考查学生对新概念的理解，考查学生获取新知识的能力和对新问题的理解探究能力.培养“四能”即发现和提出问题的能力、分析和解决问题的能力，因此必须注重过程，这里的“过程”不是指授课时要讲解，或者让学生经历知识产生的过程，甚至不是指知识的呈现方式，而是学生探究的过程、思考的过程、抽象的过程、预测的过程、反思的过程等等.

【变式3】定义：对于数列{xn}，如果存在常数p，使对任意正整数n，总有(xn+1-p)(xn-p)<0成立，那么我们称数列{xn}为“p-摆动数列”.

(Ⅰ)若an=2n-1，bn=qn(-1

提示：(Ⅰ)假设数列{an}是“p-摆动数列”，即存在常数p，总有2n-1

则(cn+2-p)(cn-p)>0，

所以c1>p，c3>p，…，c2n-1>p，

同理c2

教学启示：求解此类问题时，先研究好新定义数列的特征，然后根据此新定义去解决问题，有时还需要用类比的方法去理解新定义，这样有助于对新定义的透彻理解,透过现象看本质，就会发现它们考查的还是数学基础知识，所以说“新题”不一定是“难题”，掌握好“四基”“四能”，以不变应万变才是制胜法宝.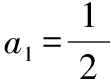

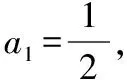
4.结束语