基于隐形载体命制的立体几何试题教学价值探索

浙江 施利强 谢小强

本文以一道2021年4月湖州、衢州、丽水三地市联考的立体几何模拟试题为例，探究基于隐形载体命制的立体几何试题的特点和教学价值.与此同时，在该题命题方式的启发下，笔者又进一步挖掘了高考立体几何试题中的隐形载体并改编得到几个试题作为训练题，以期达到培养学生直观想象核心素养的目的.

一、试题呈现

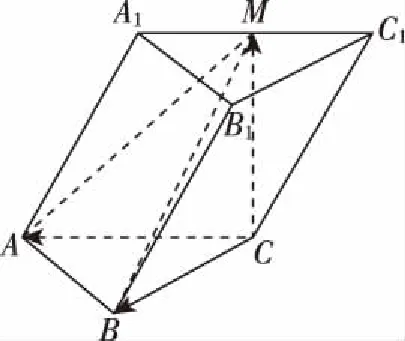
如图，已知三棱柱ABC-A1B1C1，△ABC是正三角形，四边形ACC1A1是菱形，且∠A1AC=60°，M是A1C1的中点，MB=MC.

(1)证明：AM⊥BC；

(2)求直线AM与平面BCC1B1所成角的正弦值.

本题立体模型的主要载体是三棱锥M-ABC.命题者在隐形载体M-ABC的基础上，补形得到斜三棱柱ABC-A1B1C1.由于隐形载体三棱锥M-ABC的线面之间没有特殊的平行垂直关系，补形的线面元素与隐形载体线面元素之间也没有直接关联.问题二考查的又是隐形载体中直线AM与补形平面BCC1B1的线面角，所以对学生的空间想象能力有较高要求.笔者以该题为例，先多角度解决该问题，在解决该问题的同时，充分挖掘该试题带来的教学价值.以下先从多角度呈现本题的解法.

二、解法探究

(1)证明：如图，取BC中点为D，连接AD,MD.由MB=MC得MD⊥BC.由△ABC是正三角形得AD⊥BC.

又MD∩AD=D，故BC⊥平面AMD，所以AM⊥BC.

(2)不妨设AA1=AC=2.

解析一：垂面法

设AD中点为E，平面AME交B1C1于点N，连接NE.

所以DN为AM在平面BCC1B1内的投影，所以∠END为AM与平面BCC1B1所成的角.

解析二：补形

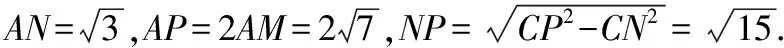
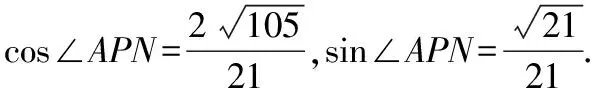
解析三：等体积法

解析四：正交建系

解析五：基底法

评注：第2问学生感到困难主要在于补形的线面元素与隐形载体线面之间没有较大的关联，隐形载体中直线AM与补形平面BCC1B1又没有给出交点，所以解析二补形的想法较为自然，但对学生直观想象核心素养有较高要求；解析一垂面法求线面角，在隐形载体的基础上，垂面隐藏于隐形载体与补形立体之间，因此，作垂面对学生的直观想象核心素养有更高的要求.但是问题一的证明给隐形垂面的显现做了铺垫，一线教师借助该解析可以进一步强调有一组异面直线垂直是三垂线法作垂面的前提；此外，基于隐形载体的命制思路使得本题的等体积法和建系法都有一定的思维量和计算量，所以考查结果并不理想.

本题是在隐形载体的基础上命制的好题，多角度的分析也给我们带来了较大地教学价值，在注重学生计算能力的同时，更应该注重学生直观想象等核心素养.平时教学过程中，我们应该强调各类解法的适用条件和范围.让学生充分挖掘条件各几何元素之间的关系，在不断的训练过程中反思感悟总结，从而提升直观想象的思维能力.

为了进一步训练学生解决该类问题的能力，在本题隐形载体的基础上，笔者又进一步挖掘得到第三问，以达到加强学生直观想象核心素养的思维能力培养的目的.

三、拓展延伸，变式训练

笔者在原题隐形载体的基础上，给出问题三：求直线CM与平面ABB1A1所成角的正弦值.

本训练题也给我们带来了教学启示和命题方向，每一道质量较高的试题都凝聚着出题者的智慧，因此我们需要充分挖掘每一道好题中的教学价值，从而能更有效地训练学生在解决立体几何问题时的直观想象核心素养.

四、回顾历年，寻找“蘑菇”

充分挖掘了模拟试题的教学价值之后，笔者意犹未尽.波利亚曾经把“数学题”比作“蘑菇”，好问题如同某些蘑菇，它们都成堆地生长，找到一个以后，应当在周围再找找，很可能在附近就有好几个.笔者回顾了近几年的浙江省高考题中的立体几何大题，也惊喜地发现了隐形载体.

其中，2019年的三棱柱的隐形载体是三棱锥A1-ABC，三棱锥A1-ABC中正△A1AC垂直于Rt△ABC，在隐形载体的基础上补形得到三棱柱ABC-A1B1C1.同时，隐形垂面△A1BC隐藏在了隐形载体与补形立体之间，很大程度上落实了直观想象核心素养.

2020年的三棱台DEF-ABC的隐形载体是三棱锥D-ABC.隐形载体三棱锥D-ABC中边长不固定，但在该载体中包含了三个固定的角∠DCA,∠DCB,∠ACB.这为垂面的构造提供条件的同时也将隐形垂面隐藏在了隐形载体内.

近两年的高考题的立体图形都是在隐形载体基础上构建得到的，并将垂面以隐形垂面的形式隐藏在了隐形载体与补形立体之中，问题的设置为隐形载体元素与补形元素之间的探究.隐形载体与补形立体之间的线面联系需要进一步挖掘，对学生的直观想象核心素养也提出了较高的要求.因此，这两个在隐形载体基础上命制的高考题也起到了较好的选拔作用.

在模拟试题和高考真题的命题启发下，笔者发现，基于隐形载体并通过一定方式补形得到的立体图形可以较好地考查学生直观想象的核心素养.因此，笔者在两个高考试题隐形载体的基础上，又进一步进行了改编，得到了以下两个改编题.并将其作为学生直观想象核心素养提升的训练题.

五、模拟题再编制

改编试题1：2019年浙江省高考试题改编题

(1)证明：BC⊥EF.

(2)求直线EF与平面BCC1B1所成角的正弦值.

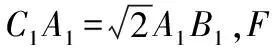
(2)解析一：垂面法

解析二：等体积法

评注：笔者在2019年的高考题的隐形载体的基础上改编得到了本试题.题干中隐形载体是三棱锥A1-ABC，它和补形立体线面之间没有紧密联系，这为隐形垂面的挖掘增加了难度，但第一问的设置为隐形垂面的显现提供了条件和思路.因此，本题可以作为训练学生直观想象的分析能力.与此同时，笔者进一步将该改编题运用到了教学实践，得到了较好的训练效果.

改编试题2：2020年浙江省高考试题改编题

(1)证明：BC⊥BD；(2)求直线DF与平面DBC所成角的正弦值.

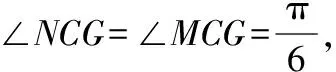
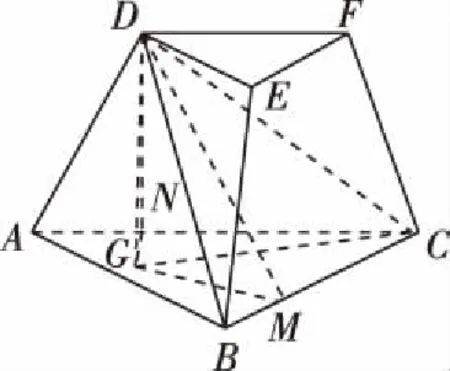
(2)解析一：垂面法

解析二：等体积法

评注：本题在2020年高考题隐形载体的基础上，去掉了原题隐形载体中面面垂直的条件，改变了载体给出的条件，增加了难度，对学生的直观想象核心素养和分析问题的能力提出了更高的要求.其中，问题一的设置为问题二垂面的作出提供了条件.问题二由于各边长不确定，等体积法具有一定的灵活性，但本问的设置进一步达到了训练学生直观想象核心素养和分析问题的能力的目的.

六、总结

以隐形载体为命题出发点的立体几何试题往往对学生的直观想象核心素养有较高的要求.从本文探究的立体几何大题命题的启发下，笔者又进行了进一步的教学反思感悟，总结得到了基于隐形载体命制的立体几何试题带给我们的教学价值.

教学价值一：立体几何的教学过程中，我们应该加强学生传统方法的训练，以利于学生直观想象的思维训练和分析解决问题的能力的培养.因此，平时应该让学生多角度地分析问题.

教学价值二：我们平时应该注重学生计算能力的培养，在隐形载体基础上命制的立体几何试题，对学生的计算能力提出了较高的要求.