重视教材 用好手中“宝”
山东 武守维
古人云:问渠那得清如许,唯有源头活水来.无论哪年的高考真题都不外乎取材于课外,得益于课内,重视对教材的挖掘,以不变应万变,相信在考场中一定会得心应手.下面以一道课本习题为例感悟教材是知识的栖息,是思维的放生园!
试题呈现:
(2019年人教A版选择性必修第三册复习参考题7第10题)甲、乙、丙三人相互做传球训练,第1次由甲将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人,求n次传球后球在甲手中的概率.
选题原因:
主要源于对数列的考查方式和方法的思考,2019年之前全国卷对数列解答题的考查不怎么热爱,但2019年之后有所增加,考查形式主要有:单纯数列的考查,数列和其他知识点(概率、函数、不等式等)交叉考查,构建数列模型考查等;新课标非常重视建模的考查,这道题可以说是概率模型,也可以说是数列模型,也可以说是概率数列模型,这类模型应引起教师及学生的思考和重视.
解法一(利用概率计算公式):设n次传球后球在甲手中的概率为pn,n=1,2,3,…,
当n=1时,甲传给乙或丙,所以p1=0,

pn+1=P(An+1)




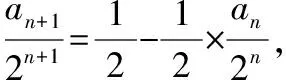
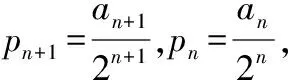



【新视角】从创新的角度看,知识的交融是一个较容易实现的方式;新颖的背景又是创新的一个着力点,我想这应该是命题专家比较青睐的地方.新教材对于建立模型解决问题是非常推崇的,这也是我们应该研究的地方.
【变式】甲、乙、丙三人相互做传球训练,第1次由甲将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人,求n次传球后球在乙手中的概率.
解法一(利用概率计算公式):设n次传球后球在乙手中的概率为pn,n=1,2,3,…,


pn+1=P(An+1)

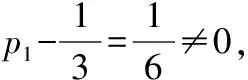

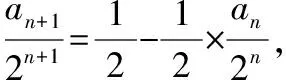
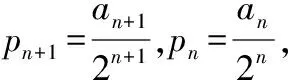



【推广】m(m≥2且m∈N*)个人相互做传球训练,第1次由甲将球传出,每次传球时,传球者都等可能地将球传给另外(m-1)个人中的任何一人,求n次传球后球在甲手中的概率.
解法一(利用概率计算公式):设n次传球后球在甲手中的概率为pn,n=1,2,3,…,
当n=1时,甲传给乙或丙,所以p1=0,

pn+1=P(An+1)





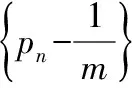

【链接高考】(2019·全国卷Ⅰ理·21)为治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得-1分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得-1分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X.
(1)求X的分布列;
(2)若甲药、乙药在试验开始时都赋予4分,pi(i=0,1,…,8)表示“甲药的累计得分为i时,最终认为甲药比乙药更有效”的概率,则p0=0,p8=1,pi=api-1+bpi+cpi+1(i=1,2,…,7),其中a=P(X=-1),b=P(X=0),c=P(X=1).假设α=0.5,β=0.8.
(ⅰ)证明:{pi+1-pi}(i=0,1,2,…,7)为等比数列;
(ⅱ)求p4,并根据p4的值解释这种试验方案的合理性.
解析:(1)X的所有可能取值为-1,0,1.
P(X=-1)=(1-α)β,
P(X=0)=αβ+(1-α)(1-β),
P(X=1)=α(1-β),
所以X的分布列为

X-101P(1-α)βαβ+(1-α)(1-β)α(1-β)
(2)(ⅰ)证明:由(1)得a=0.4,b=0.5,c=0.1.
因此pi=0.4pi-1+0.5pi+0.1pi+1(i=1,2,3,…7),故0.1(pi+1-pi)=0.4(pi-pi-1),
即pi+1-pi=4(pi-pi-1).又因为p1-p0=p1≠0,所以数列{pi+1-pi}(i=0,1,2,…,7)是首项为p1,公比为4的等比数列.
(ⅱ)由(ⅰ)可得
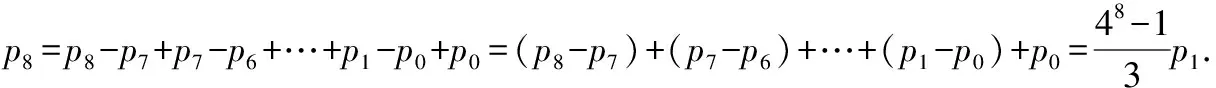


考点分析:
概率分布列,概率的意义,等比数列的定义(证明),等比数列求和,解方程等.
题目背景:
以概率为背景构建数列,通过数列的求解,解决概率问题.
学生视角:
题目太长,心烦意乱,容易放弃;背景新颖,数列和概率结合,并且概率压轴,心理落差太大,导致崩溃.
教师视角:
题目不复杂,只要心平气和、按部就班地去做,应该能做出来,就是学生可能会有很多不理解的地方,比如空降的递推关系怎么来的,为什么求p4,pi等一系列疑问无法解答.
专家视角:
从“治疗疾病”的问题情境出发,不仅体现了“为人民服务”的初心,而且是与学生息息相关的真情境;强调了数学与生物、化学、语文等学科的综合应用;学生需要通过阅读与理解,把实际问题进行高度抽象,建立概率模型,落实了数学抽象和数学建模的核心素养,而把概率和数列放在一起考,又突出了对学生创新能力的考查.
笔者体会:


