基于社会学习的粒子群优化算法的电力系统稳定器参数协调优化设计

张 程， 邱炳林， 刘佳静， 匡 宇

(1. 福建工程学院电子电气与物理学院， 福建 福州 350118； 2. 智能电网仿真分析与综合控制福建省高校工程研究中心， 福建 福州 350118)

1 引言

随着我国电力网络的建设发展，各区域电网之间实现互联互通，但同时也伴随着一些问题,如低频振荡现象在电力网络中日益凸显[1-3]。对于低频振荡的抑制，通常采用的措施是在励磁系统中装设电力系统稳定器，由于该方法较为经济且有效而被广泛接纳[4,5]。电力系统稳定器(Power System Stabilizer, PSS)抑制低频振荡的效果取决于其参数整定的效果，对于传统方法整定的PSS参数通常无法在最大程度上发挥出其抑制低频振荡的效果。为此，优化PSS参数成为一个必不可少的环节，而PSS参数的优化实质上就是寻找一组参数的最优组合，使系统低频振荡模式的阻尼能够在最大程度上得到优化[6-8]，其中，较为常用的优化方法如粒子群算法[9](Particle Swarm Optimization algorithm, PSO)，诸如此类的方法已较为成熟，但在优化过程中常因粒子早熟而易于陷入局部最优。文献[10]则利用粒子群理论提出了一种改进的粒子群优化算法，虽然算法的性能在一定的程度上得到了提高，但其寻优速率较低，寻优的准确性也有待进一步考察。

对于此类优化算法性能的提升，总结归纳为以下几个方面[11]:第一类为使用粒子群算法中参数的自适应控制策略；第二类为混合粒子群算法，将粒子群算法与其他搜索策略相结合；第三类为粒子群算法在邻域控制中引入新的拓扑结构，以增强群体多样性，从而缓解过早收敛；第四类为多群PSO，多群粒子群算法背后的主要思想是通过在不同群之间交换信息来增强群的多样性；第五类出于提升粒子群算法执行的效率与减小其运行的内存，而对算法本身的内部结构进行调整或修改。

为此，将社会学习机制引入到粒子群算法中，社会学习的优势在于其允许个人向他人学习行为，而不会产生个人试错的成本，社会学习粒子群优化算法(Social Learning Particle Swarm Optimization algorithm,SLPSO)与经典粒子群算法不同，在经典粒子群优化算法中，其粒子是基于历史信息进行更新的，而社会学习粒子群优化算法中的每个粒子都是向当前群体中任何更好的粒子(称为演示者)学习，该算法是根据粒子的适应度进行排序的，除了最好的粒子之外，所有粒子都将通过从适应度更好的粒子中学习更新[12]。

本文将SLPSO应用于PSS参数的寻优工作中，与大多数粒子群优化算法优化PSS参数不同，基于社会学习的粒子群优化算法是在一个排序的群上执行的，其粒子不是从历史最佳位置学习，而是从当前粒子群中任何更好的粒子学习，因而本文对于PSS参数寻优所得的结果更为准确，其优化效果也更好。通过四机两区的仿真算例表明，本文方法解决了常规优化算法如粒子群优化算法优化PSS参数中存在的收敛性差、容易陷入局部最优、优化效果差等问题，即通过将SLPSO优化算法应用于PSS参数的寻优中，其PSS的抑制效果和稳定性都得到了较大的提升。

2 问题的模型描述

对于电力系统的线性化数学模型表示如下：

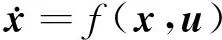
(1)

(2)

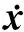
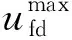
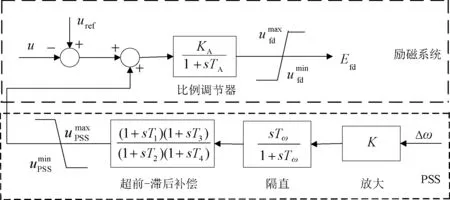
图1 PSS原理图Fig.1 Schematic diagram of PSS

通过PSS产生的辅助控制信号uPSS作用于励磁系统中，从而在一定程度上能够实现对系统整体的阻尼形成一个控制，其传递函数如下所示[17,18]：

(3)

式中，T1和T3为超前时间常数；T2和T4为滞后时间常数；K为其增益；Tω为隔直时间常数；Δω为输入的角频率；s为拉普拉斯变换中的变量。

3 基于社会学习的粒子群优化算法

本文提出的社会学习粒子群优化算法解决了经典PSO中存在的粒子早熟收敛和优化后期种群多样性丢失等问题。基于社会学习的粒子群优化算法的步骤归纳如下[19]：

(1)初始化含有N个粒子的群体P(t)，P(t)中不同的粒子保持着各自的随机初始化行为向量xi(t),表示优化问题的候选解；种群大小和社会影响因子分别设为N和ε，D表示维数，β用以调节影响因子的大小，可表示如下：

(4)

(2)根据步骤(1)初始化所得到优化问题的候选解，进行每一个粒子适应度值的计算，并由各粒子适应度值的大小进行排序。

(3)经过步骤(2)的排序后，将所有适应度值非最优的粒子根据式(5)向最优粒子进行学习，其学习过程如式(5)所示，非最优粒子的更新矫正为ΔXi,j(t+1)，以此更新矫正每一个非最优粒子的位置，而对于适应度值最佳的粒子则此次暂时不作更新。

ΔXi,j(t+1)=r1ΔXi,j(t)+r2Ii,j(t)+r3εCi,j(t)

(5)

式中，Ii,j(t)为在j维下任一粒子k与粒子i的位置距离；Ci,j(t)为整体粒子的平均位置与在j维下的粒子i的距离；r1、r2及r3分别为0～1的权重系数。更新操作分为三部分，其一是与经典PSO中的惯性成分相同；其二为向当前最优粒子Pbest学习部分，其三则为向当前群中所有粒子的平均行为gbest学习部分，各部分的具体计算如式(6)～式(8)所示：

Ii,j(t)=Xk,j(t)-Xi,j(t)

(6)

(7)

(8)

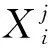
(4)步骤(3)中的每一个非最优粒子都能够向最优粒子进行学习，从而非最优粒子得以自我更新，以产生新一代整体更优的粒子群；此后根据步骤(2)、步骤(3)循环更新粒子群，此时的“被学习对象”可能是前一次适应度值最优的粒子，也可能是更新矫正后的某一粒子，其表达式如下所示：

(9)

式中，pi和pi(t)分别为当前最优适应度值和某个粒子t的适应度值，通过大小对比决定粒子是否更新。

(5)在上述过程中各粒子不断找寻最优参数，直至迭代寻优结束。

算法中各粒子的更新操作示意图如图2(a)所示，能够直观地看出算法是如何进行最佳粒子的搜索，并给出算法的流程图如图2(b)所示，其中，P(0)为含有N个粒子的初始群体。

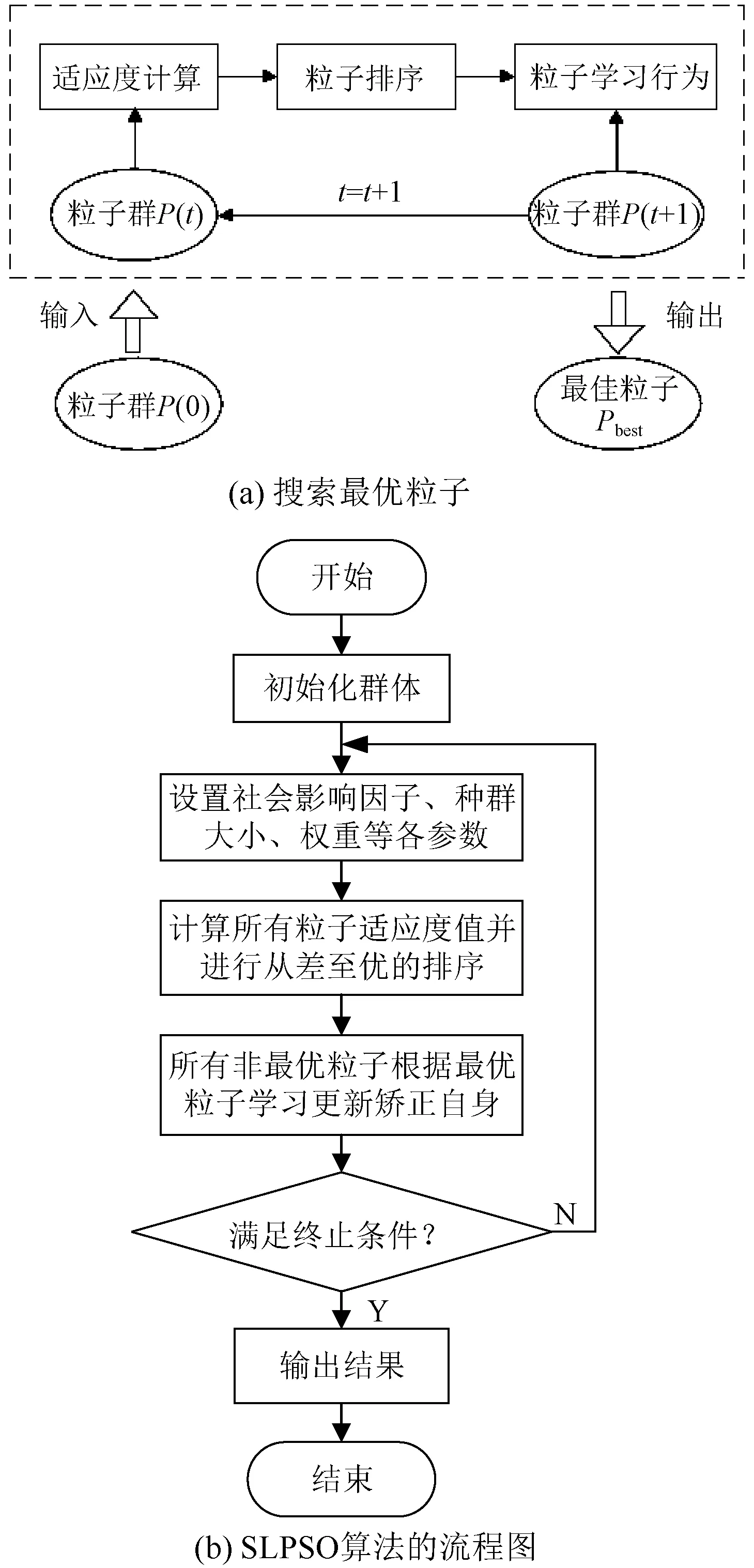
图2 社会学习粒子群优化算法Fig.2 Learning particle swarm optimization algorithm

4 多机系统PSS的参数优化

4.1 优化目标建模

本文将采用多目标函数协调优化各PSS参数；在线性系统中，特征值λ取决于状态矩阵A，而λ又决定了系统的整体稳定性；通过系统中的特征值λi可以确定出系统中各模态的阻尼比ξi，而阻尼比通常能够反映出系统的动态性能。其特征值和阻尼比的表达式如下[20]：

λi=σi±jωi

(10)

(11)

式中，σi为阻尼因子；ωi为振荡角频率。

在系统受到扰动后，为了使其尽快回到原有稳定运行状态，系统的阻尼比就要尽可能地最大化；在目标函数寻优过程中，应使其满足在ξ0≤ξi,j的范围下对最优值进行搜索，本文采用的是多目标优化，而另一优化目标将以特征值实部作为标准，为获取尽可能小的阻尼比和特征值实部，上述问题就转化为求取如下目标函数的最小值：

(12)

式中，n为运行方式的数量；m为机电模式的数目；α、β为多目标函数的权重；ξ0和σ0为本文所设置的阈值，ξi,j和σi,j分别是第i种运行状态下的第j个机电振荡模式的阻尼比和机电振荡模式的特征值实部。

在算法的寻优过程中，对阻尼比和特征根实部也需要进行相应的约束，在该约束范围下进行最优目标函数的搜索，以获取在某一运行参数下最大的阻尼比和最小的特征根实部，其约束范围如式(13)及图3所示。

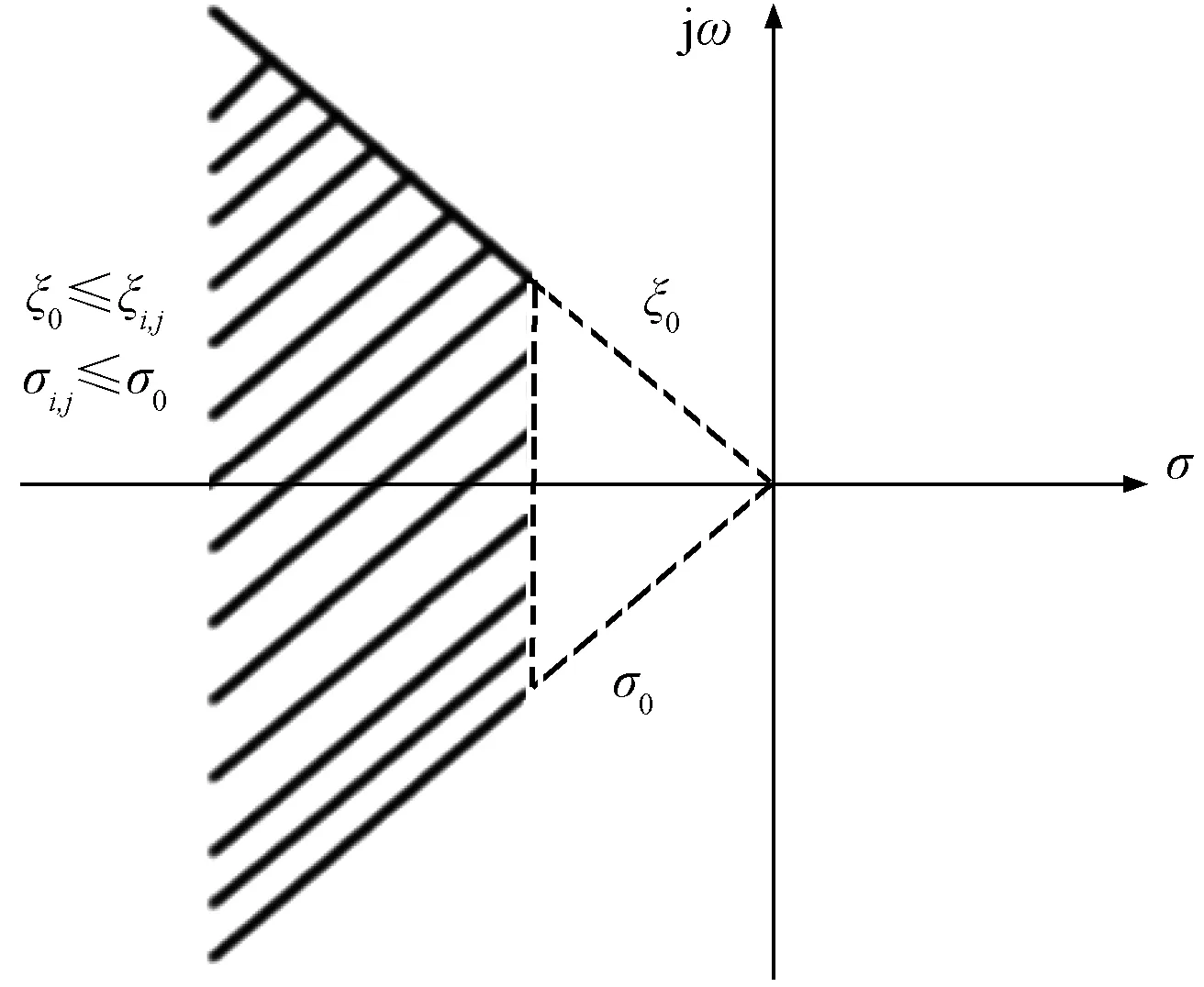
图3 目标函数在复平面中的期望区域Fig.3 Expected region of objective function in complex plane

(13)

在目标函数中，本文将α、β的取值限于0～1之间，由于阻尼比对振荡的抑制体现更为直观，较大的阻尼比抑制振荡的效果自然更好，所以本文对阻尼比所取的权重更大，α、β分别取0.8和0.2。

如图3所示,对于协调优化PSS参数的问题，就是要使系统的阻尼比最大化，使其特征根不断地向复平面的左半平面移动，在最大程度上地远离虚轴，使各机电振荡模式的阻尼比达到预定的要求，以此来提高电力系统的整体稳定性。

PSS参数的设置合理与否，需满足以下条件：首先，对于投入PSS后的机组，其主导振荡模式的阻尼比应有所提升；其次，对于没有投入PSS的机组，各自的阻尼比没有出现一定程度上的恶化；最后，对于多机系统而言，不同的PSS之间需要相互协调以达到整体最优的效果。

各PSS需优化的参数分别为增益K以及时间常数T1和T3，而对于有i个PSS的系统则需优化的参数就有3i个，即优化参数的维数为3i；各个参数的优化约束条件如下所示：

(14)

式中，Kmax、Kmin分别为增益取值的上、下限；T1,max、T1,min和T3,max、T3,min分别为超前和滞后时间常数取值的上、下限。

在以上约束条件且满足该目标函数的需求下，使PSS产生最好的抑制效果，从而使系统的阻尼比和各机电振荡模式的特征根实部得到最大化。

4.2 算法优化流程

本文算法SLPSO是基于Matlab所编写，通过该算法调用多机系统仿真模型，不断地将算法寻优得到的参数值向PSS模块赋值，对于每一个PSS模块，需要赋值的参数分别为K、T1、T3，其算法优化参数的维数取决于装设PSS的个数。

以下是基于本文社会学习粒子群优化算法优化PSS参数的步骤，归纳如下：

(1)根据事先设置的系统故障，通过仿真系统的故障振荡模式，确定出本文所需装设PSS的个数与位置。

(2)SLPSO算法初始化种群，完成算法相关参数的设置工作，将仿真模型PSS模块中需要优化的参数设置为外部变量。

(3)通过Matlab中的sim函数，调用仿真模型以此得到相关的振荡模态，通过模态分析和基于SLPSO算法得到目标函数以及求取适应度值，分析、比较、保留当前的最优适应度。

(4)由SLPSO算法不断地搜索最优参数组合，非最优粒子不断地向最优粒子进行社会学习，直至SLPSO优化算法寻优迭代过程结束，从而得到最优的PSS参数优化结果，并输出目标函数的收敛曲线，根据收敛曲线可观察算法的寻优过程。

基于SLPSO算法优化PSS参数的寻优工作流程如图4所示。

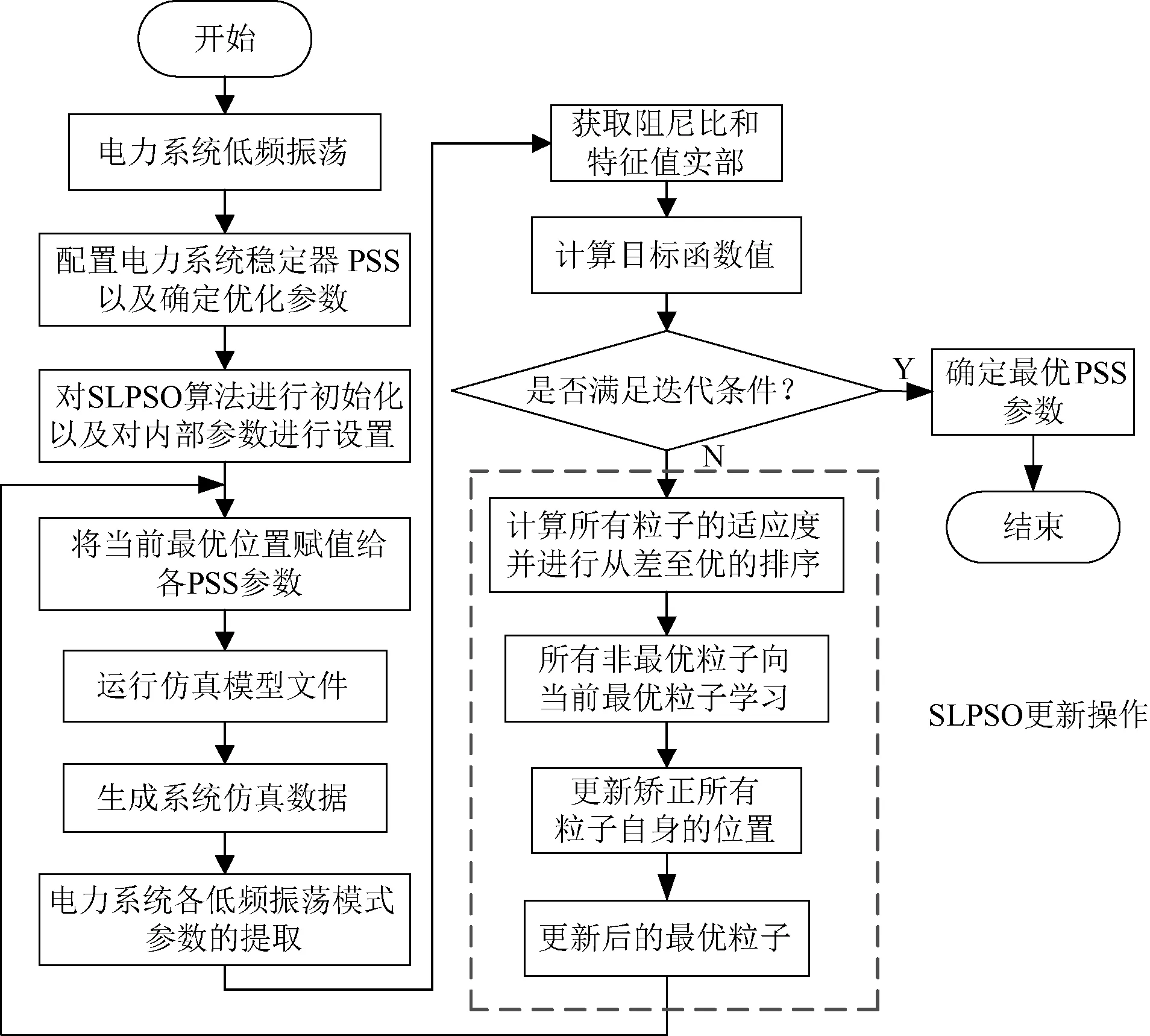
图4 SLPSO算法优化PSS参数流程图Fig.4 Flow chart of optimizing PSS parameters by SLPSO algorithm

5 测试函数

为观察SLPSO算法的基本性能,采用标准测试函数：Schaffer函数和Rastrigin函数，分别对本文所提的SLPSO优化算法进行测试,其函数表达式分别表示为如下形式：

(15)

(16)

已知两个测试函数都具有无数个极小值点，且都在(0,0)处取得最小值0；现分别使用PSO、人工鱼群算法(Artificial Fish Swarm Algorithm,AFSA)以及SLPSO，对上述两个标准测试函数分别进行1 000次的迭代寻优，寻找函数的最小值。

其迭代曲线如图5所示，由图5可知，PSO以及AFSA算法收敛速度都较慢，在迭代初期甚至都因陷入局部最优而只找到测试函数的次优值，而本文所提的SLPSO算法则能够在迭代初期就较快地找到全局最优值，其原因是因为算法SLPSO具有一定的社会学习能力，各粒子能够不断地向最优粒子学习，能够更快地找到全局最优值。

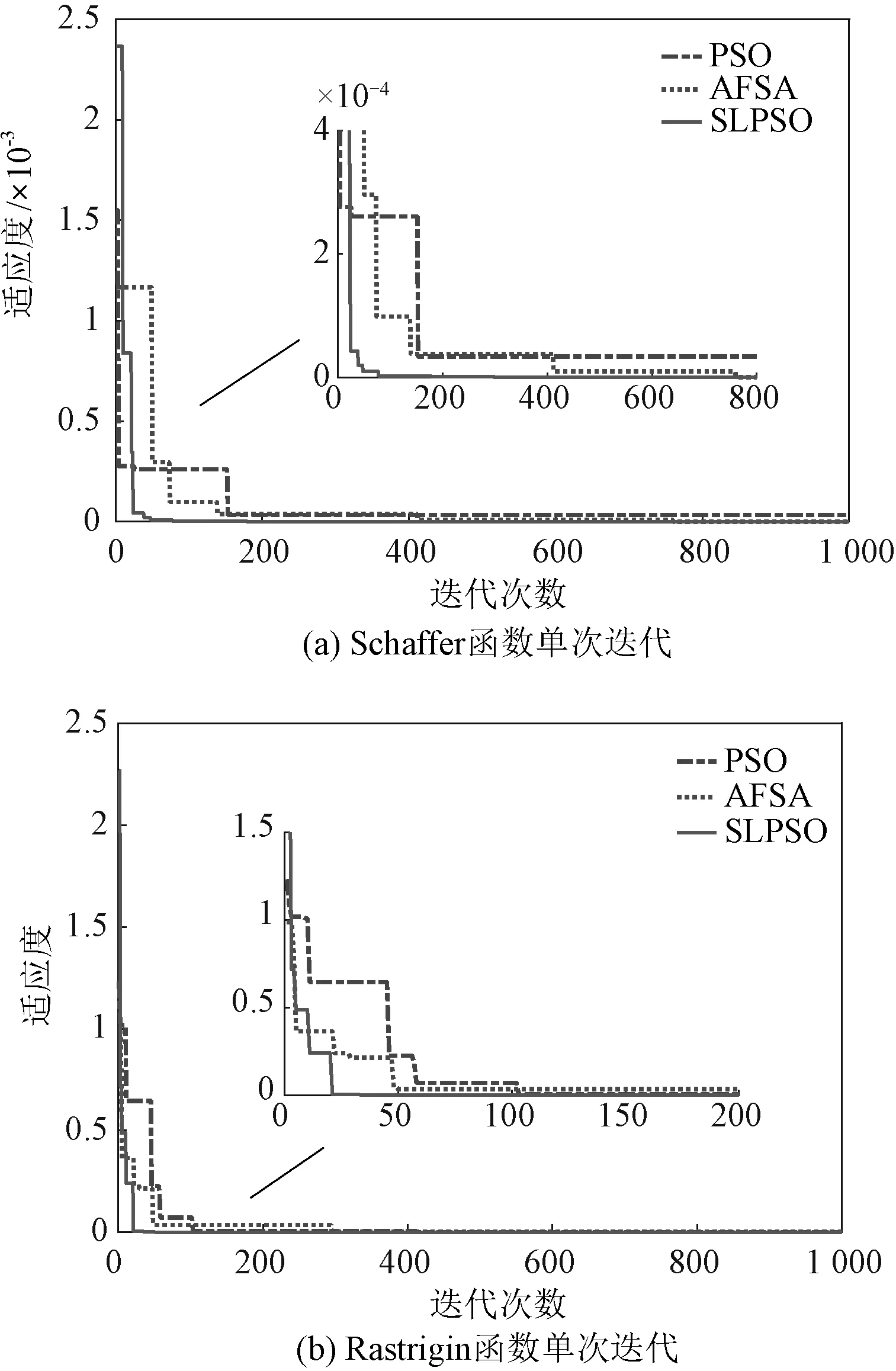
图5 测试函数单次迭代曲线图Fig.5 Single iteration graph of test function

为有效避免单次运行结果的偶然性，现分别对AFSA、PSO、SLPSO三种算法进行100次实验，每次实验包含1 000次的迭代寻优，通过对每个算法的1 000次迭代寻优求取均值，随即得到三个算法各自均值迭代曲线，所得均值曲线如图6所示。由图6可知，SLPSO算法的性能较好，并且收敛速度较快。

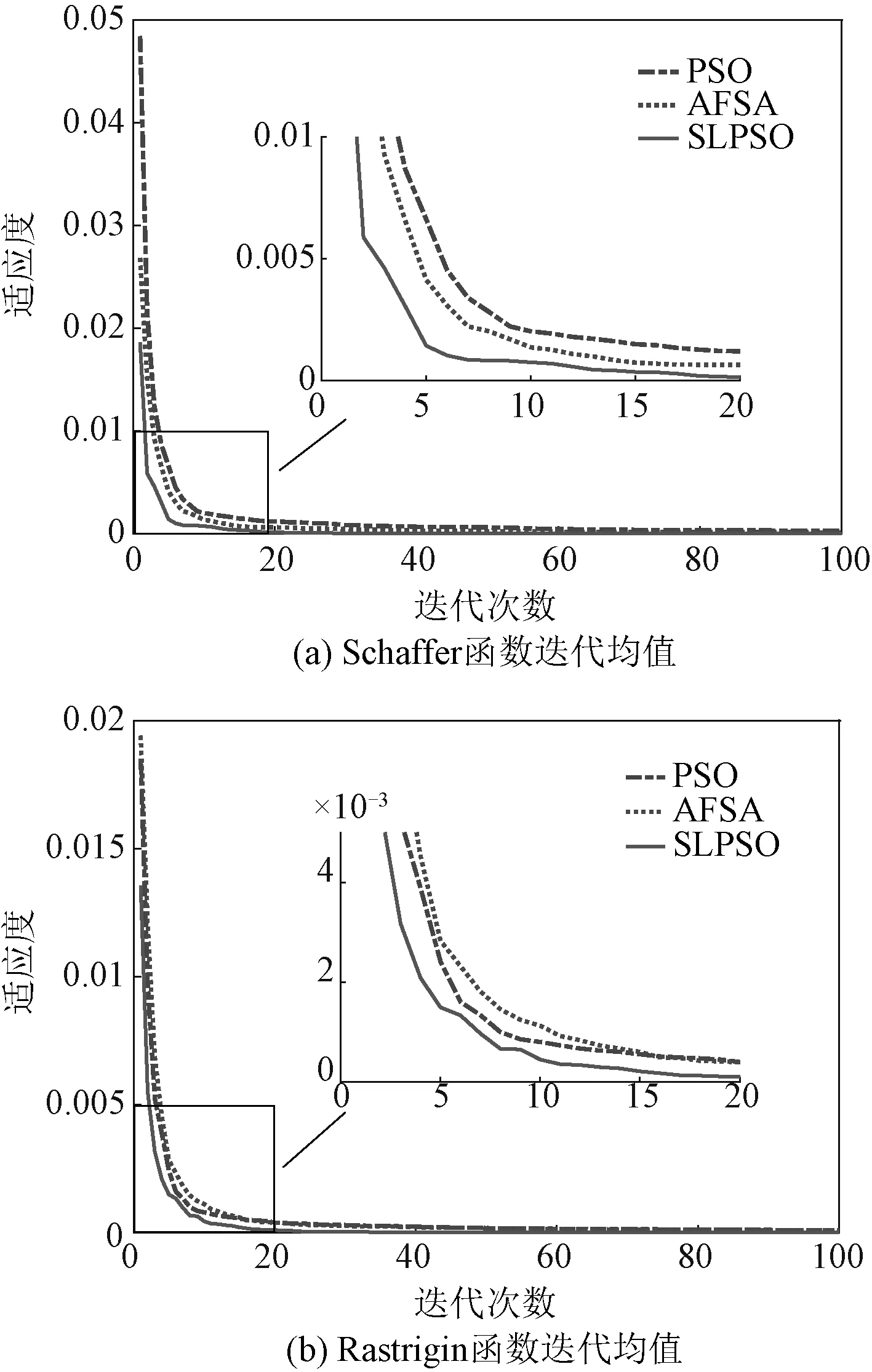
图6 测试函数迭代均值曲线图Fig.6 Test function iterative mean curve

为更好地观察各算法在测试函数中的表现，现将单次迭代寻优数据分为case1：迭代前期(迭代次数200时)、case2：迭代后期(迭代次数700时)、case3：迭代均值数据，其三组数据(最优值)见表1。首先，在迭代初期，本文算法收敛速度较快，并且在迭代后期所找到的最优值也更接近实际目标值0；其次，在进行1 000次的迭代寻优结果中，本文算法平均每次所找到的最优值也更接近0，由测试信号可知，本文算法寻优能力更为出色。

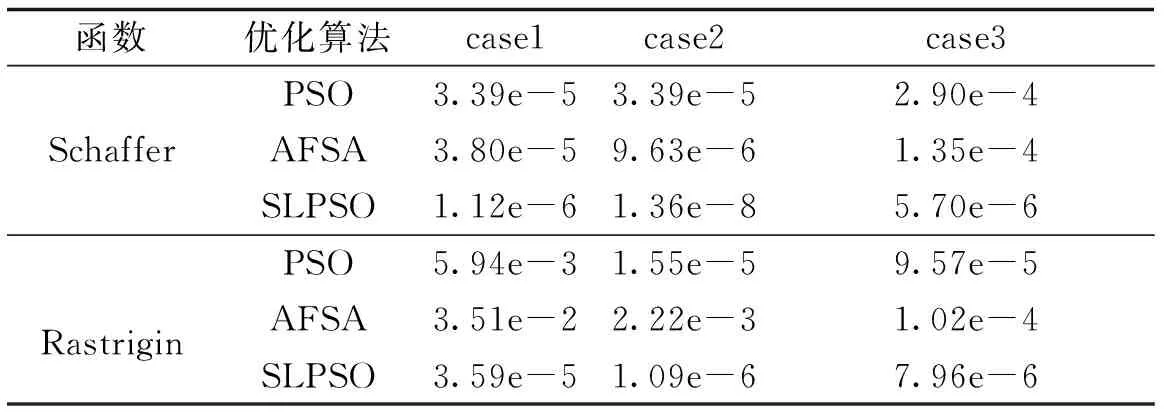
表1 测试函数寻优结果对比Tab.1 Comparison of test function optimization results

6 IEEE四机两区

6.1 小干扰仿真

本文将采用社会学习粒子群优化算法应用于多机系统的仿真模型中，SLPSO算法原理简单，是一种针对优化决策问题简单易行的优化参数算法，在实际应用中只需调试好算法本身所固有的参数，基于此，将其投入四机两区系统中，如图7所示，该多机系统采用四机两区系统，左、右两区域分别由发电机G1、G2和发电机G3、G4等组成。本文将在发电机2和发电机4上同时设置故障，该故障为在1 s时刻，对上述两台发电机励磁电压处设置5%的方波阶跃扰动，1.1 s时结束。

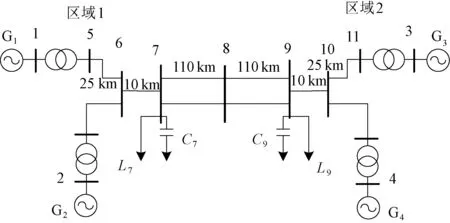
图7 四机两区系统Fig.7 Four-machine two-zone system

在该故障的设置下，系统产生低频振荡，通过对该振荡模式的分析，确定出在发电机2和发电机4上安装PSS能够更有效地抑制系统振荡。经仿真分析，预设的两台PSS都起到了抑制系统振荡的作用，但预设的PSS参数都无法在最大的程度上抑制系统振荡，因此需要对各PSS的参数进行协调优化，以达到最好的抑制效果，需要优化的参数分别为两台PSS各自的一个增益K和两个时间常数T1、T3，共6个参数。

本文将使用AFSA、PSO以及SLPSO分别对上述PSS的6维参数进行1 000次的迭代寻优，搜索最优的PSS参数组合，对本文而言，需要在满足目标函数的基础上尽可能地使适应度函数值最小，从而找到最大阻尼比，三种算法的寻优迭代曲线如图8所示。

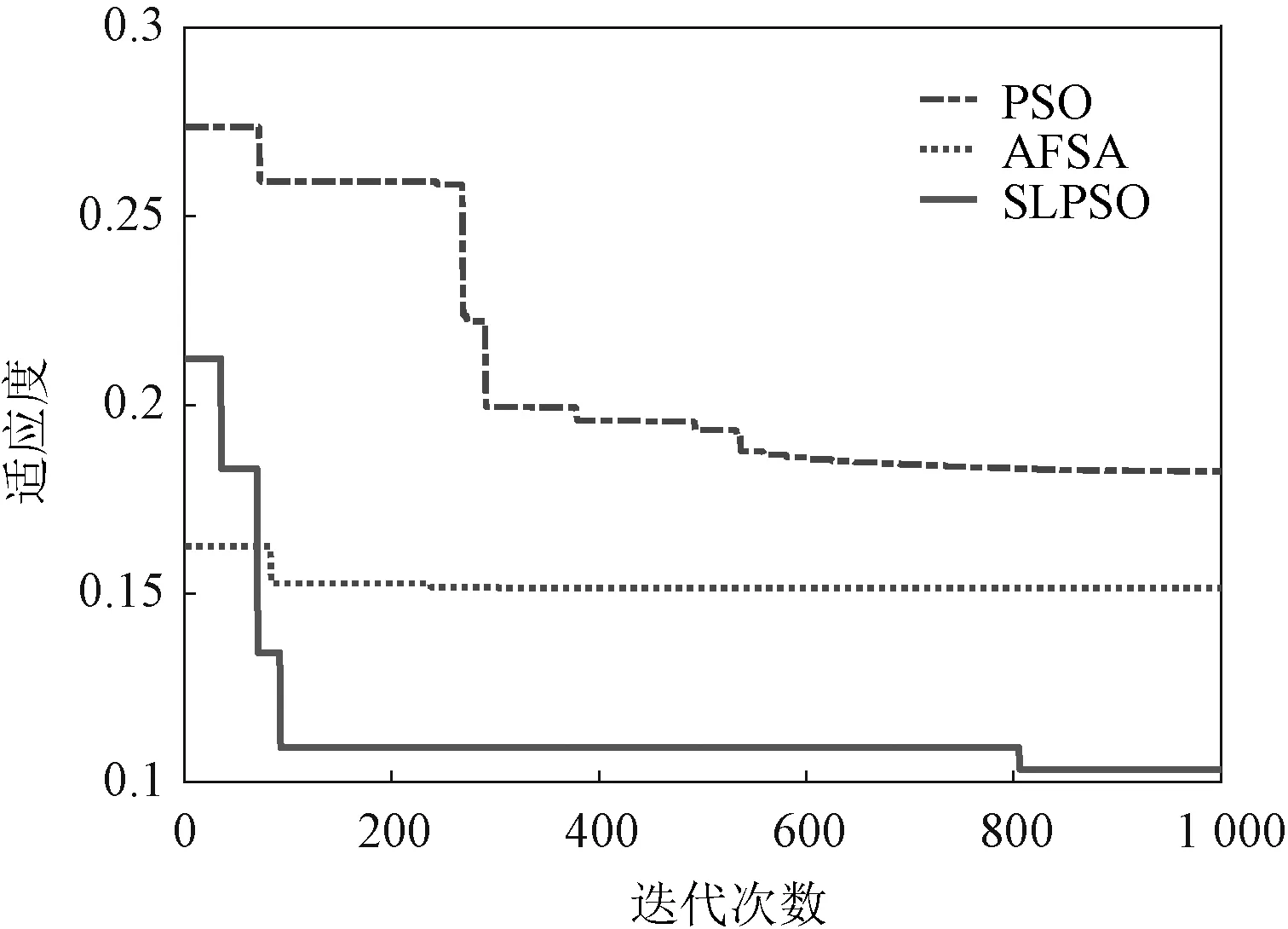
图8 优化算法迭代寻优曲线Fig.8 Iterative optimization curve of optimization algorithm

由图8可知，AFSA算法和PSO算法在1 000次迭代结束前都能找到相对较优的PSS参数组合，但上述算法的优化结果较SLPSO显然较差，本文SLPSO算法能够在迭代初期就快速地找到全局最优值，且随着迭代次数的增加不断地向最优值逼近，因此能够取得更好的优化结果；所得优化参数见表2。

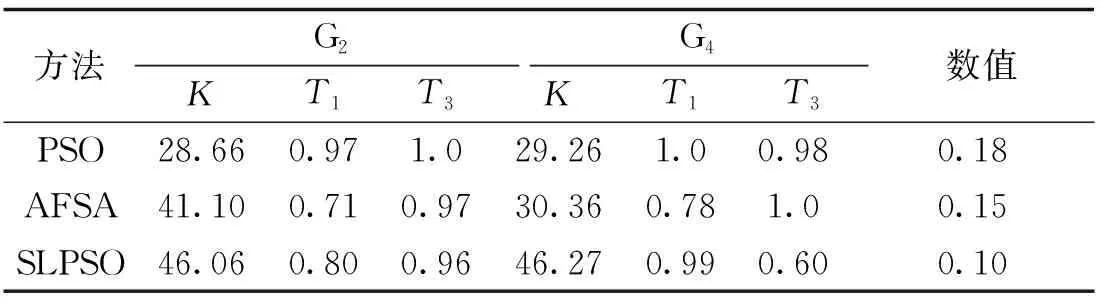
表2 三种算法所得PSS参数组Tab.2 PSS parameter sets obtained by three algorithms

当系统受到扰动时，系统两区域之间的联络线上发生有功功率的增幅振荡现象，如图9(a)所示，若不加以及时抑制，系统的运行工况将会持续恶化直至系统的两区域之间发生解裂，在默认的PSS参数下，功率振荡现象能够有效地被抑制，但抑制的过程所需时间较长，较长的故障时间则增加了系统严重失稳的风险；现将本文所提出的SLPSO算法寻找得到的优化参数应用于PSS参数的设置中，由图9可知，PSS能够快速地对有功功率的振荡进行抑制，抑制所费时间也仅在4.5 s以内。

随后分别使用PSO、SLPSO以及AFSA算法所得的最优PSS参数对PSS进行设置，对比三种算法抑制联络线有功功率振荡的效果，如图9(b)所示，通过观察可知，在PSO和AFSA算法所得参数设置下，PSS完全抑制住振荡的时间需要在10 s左右，相比于未优化PSS参数的抑制效果，已有较大的提升，但相较于本文SLPSO优化方法，明显抑制效果差，因为本文算法能够在4.5 s以内甚至4 s左右就完全抑制住振荡的持续进行，表明SLPSO算法能够搜索出更优的PSS参数组合，使PSS抑制低频振荡的效果最大化，充分体现了本文算法的优越性。

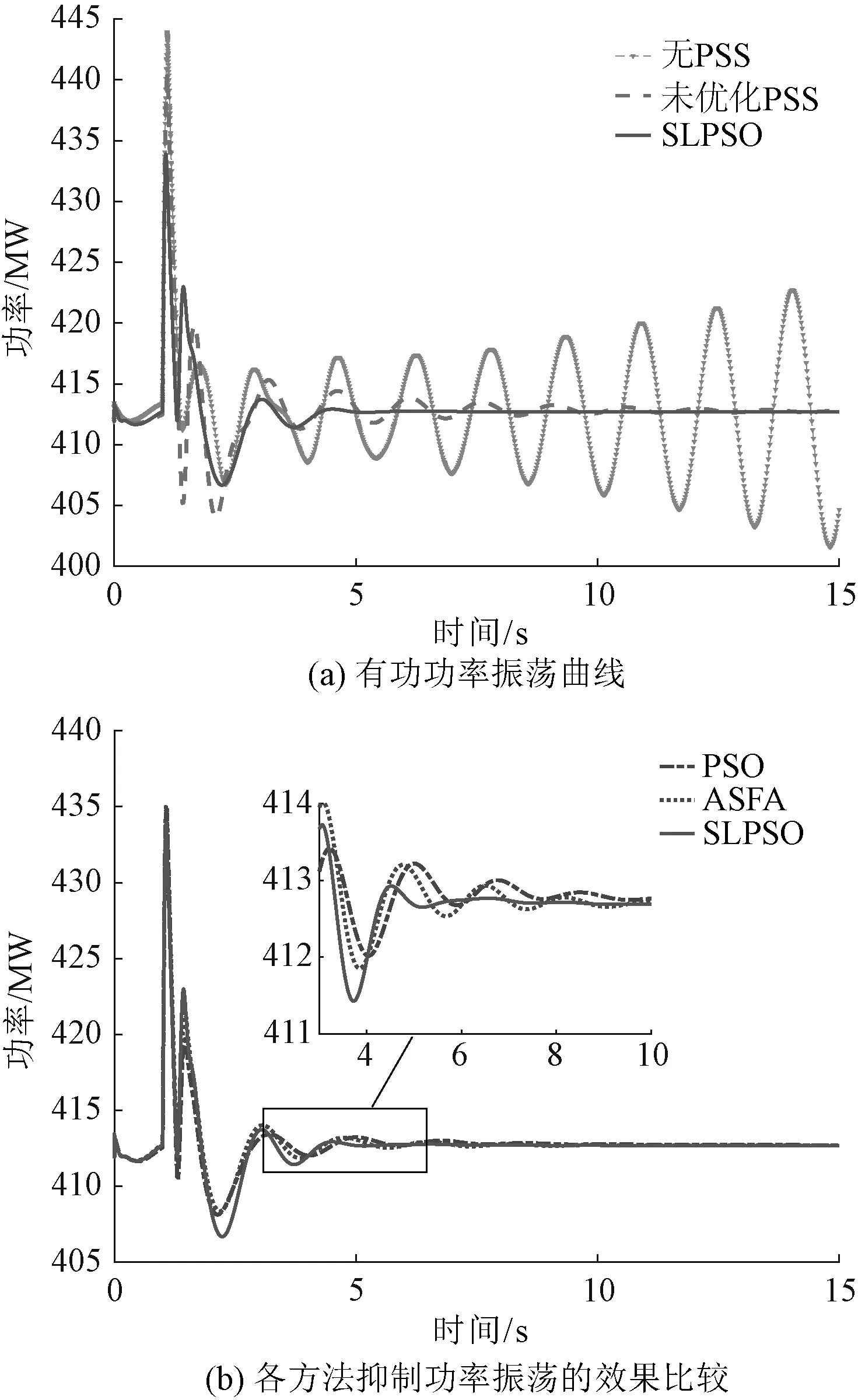
图9 联络线有功功率振荡曲线Fig.9 Active power oscillation curve of tie line

当系统受外界干扰时，各台发电机的转速和功角都将发生相应的振荡，如图10(a)和图10(b)所示，以发电机G1为例，若没有外加措施加以抑制，其转速r和功角δ的相对振荡都将无法自行平息；图10中分别使用参数未优化的PSS以及PSO、AFSA和本文所提SLPSO算法优化后的PSS，对上述多种情形下的振荡抑制过程进行对比分析，得出以下几点结论，首先，在各算法对PSS参数的优化下，其发电机的转速和功角的相对振荡都能够在不同程度上被加以抑制，加快振荡的平息；其次，就抑制效果来说，本文的SLPSO算法优化后的参数能够在最大程度上发挥出PSS的抑制效果；最后，由图10中的放大部分可以看出，就振荡幅值来说，本文算法相比于其他算法优化下的PSS抑制效果，其振荡幅值更小，即振荡抑制过程中的过冲更小。

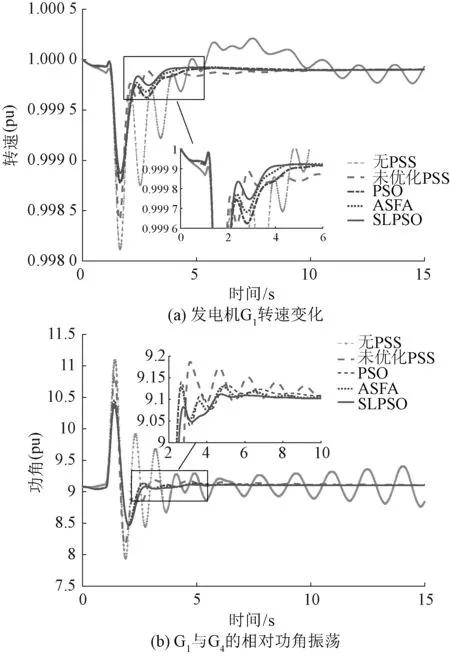
图10 发电机转速与功角的变化曲线Fig.10 Variation curve of generator speed and power angle

为了直观地看出系统变化，表3列出了系统在配置不同优化参数下的PSS仿真分析结果，并列出其机电模式的特征值分布，如图11所示，在无PSS状态下，机电模式均靠近虚轴，甚至越到了复平面的右半部，说明系统已不稳定或达到临界稳定状态，而配置上按照本文SLPSO优化整定的稳定器参数后，其特征值全部移动到期望区域内，增强了每个模态的阻尼比，与PSO、AFSA相比较而言，整体特征根的分布也有了明显的改善。

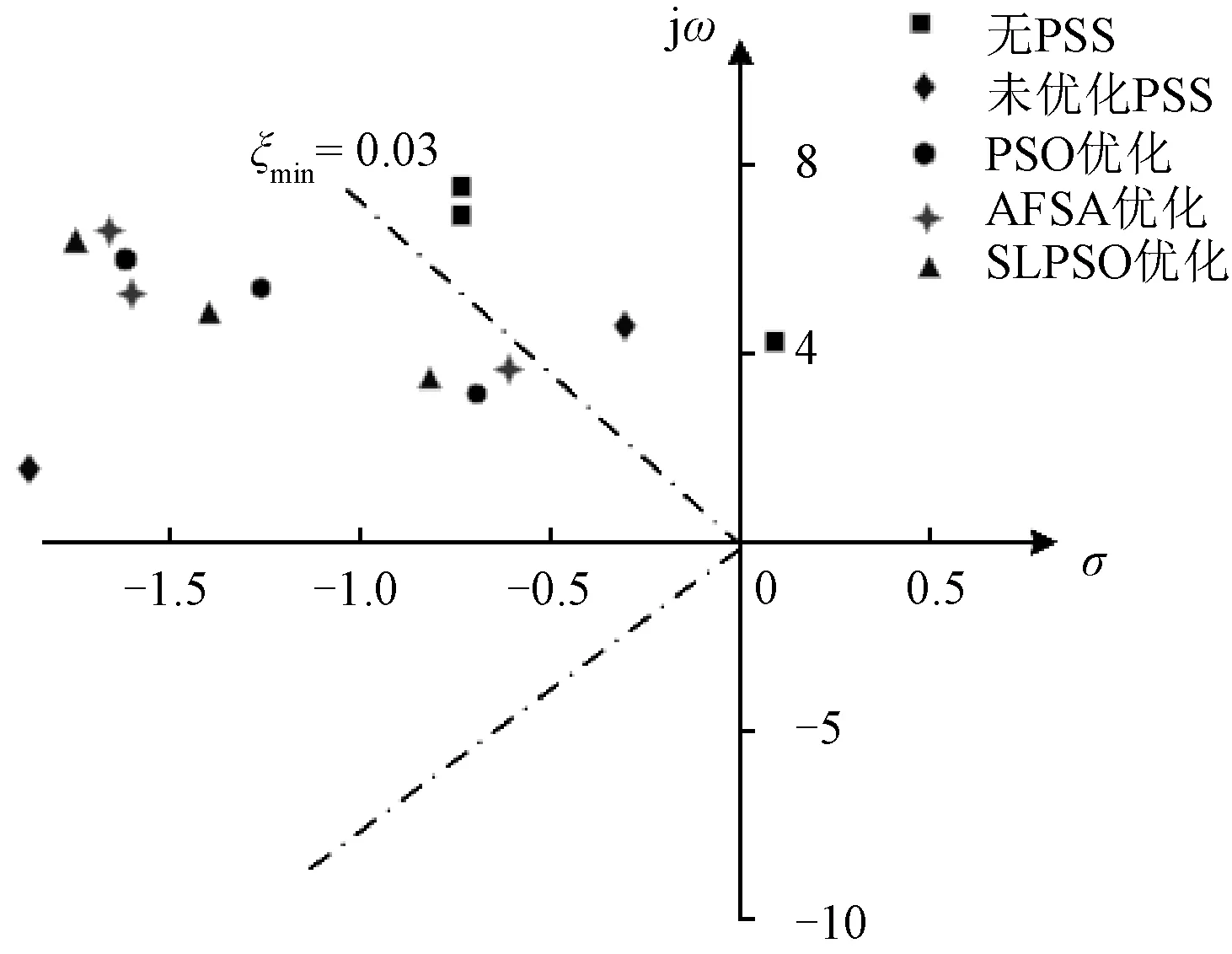
图11 机电模式特征根分布图(小干扰)Fig.11 Characteristic roots distribution chart of electromechanical mode

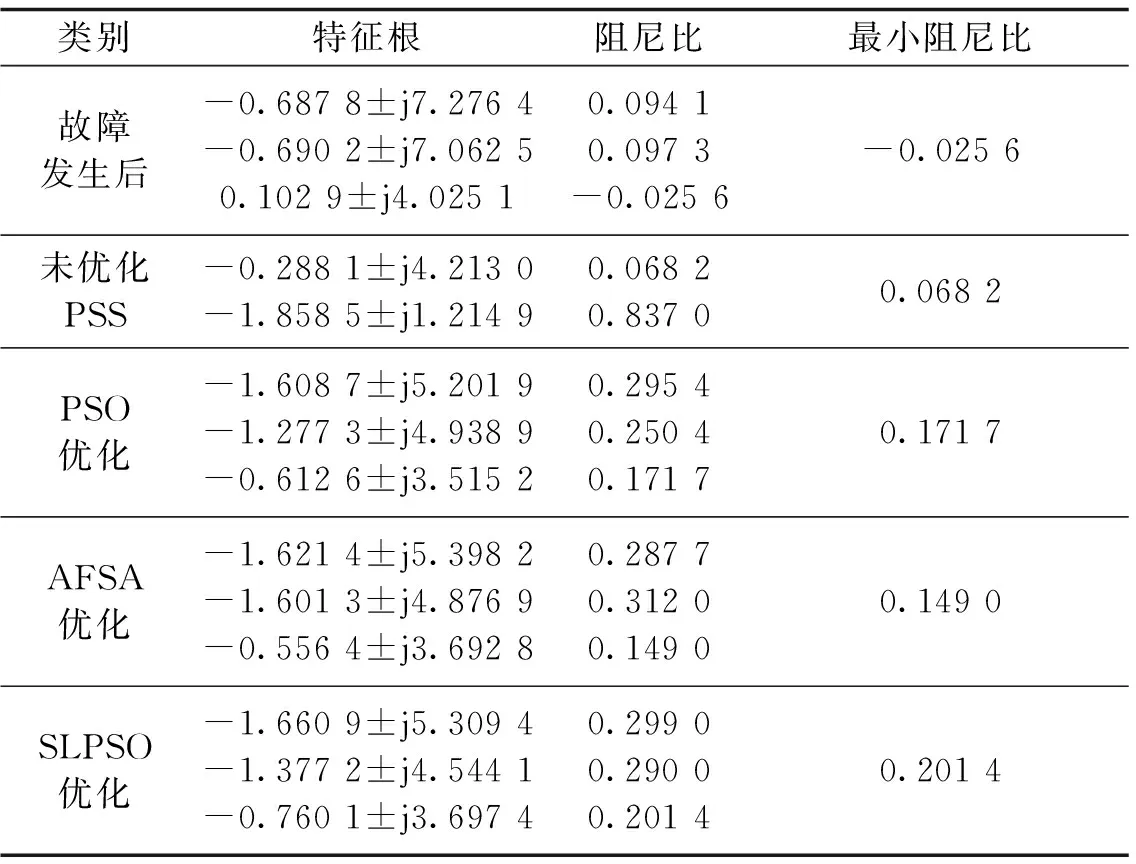
表3 各方法优化PSS后系统的特征根及阻尼比Tab.3 Characteristic root and damping ratio of system after designing PSS by different methods

6.2 大干扰仿真

为进一步说明本文算法整定PSS参数的实用性，现进行大干扰的仿真分析；故障设置如下，在1～1.2 s时系统的两区域之间发生三相接地短路故障，持续时间0.2 s；其联络线上发生的有功功率振荡状况如图12(a)所示，由图中曲线可知，未加PSS时联络线上的功率振荡成增幅振荡状态，对于整个系统的安全稳定运行将造成较大的影响，严重时甚至使两区域之间的运行解裂；图12(b)、图12(c)给出发电机G1的转速振荡曲线以及G1相对于G4的相对功角振荡曲线，由图12可知，在本文优化算法的参数整定下，其PSS能够最大程度上对系统的振荡进行有效的抑制，相比于其他算法优化而言，本文优化算法所整定的参数使PSS在抑制振荡的过程中，其振荡幅值也有所减小。

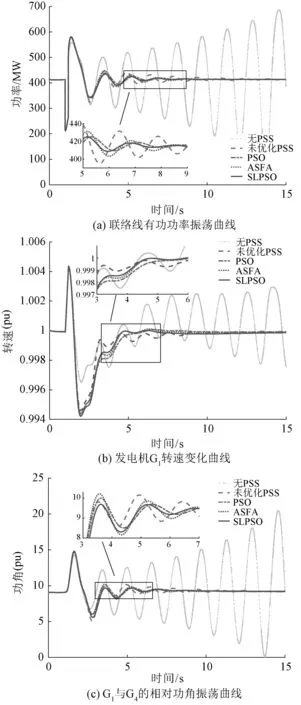
图12 大干扰下的各振荡状况Fig.12 Oscillation conditions under large interference

本文优化的主要目标是将系统特征根往虚轴左部移动，从而尽可能地最大化阻尼比和特征根的实部，观察表4和图13，在投入本文SLPSO优化后的稳定器参数后，整体的特征根分布全部往复平面的左半部分移动，而将各算法优化过后的PSS参数投入应用，都在一定程度上增强了系统的稳定性，特别是对于本文SLPSO所整定的PSS参数，能够在最大程度上将PSS的功效发挥出来，其特征值在尽可能地往左半平面移动，使得系统趋于稳定，并且由表4可知，SLPSO算法优化后的机电振荡模式特征根的最小阻尼也明显大于其他优化算法所得到的最小阻尼，可见在本文算法的优化下，其系统的稳定性更胜一筹。

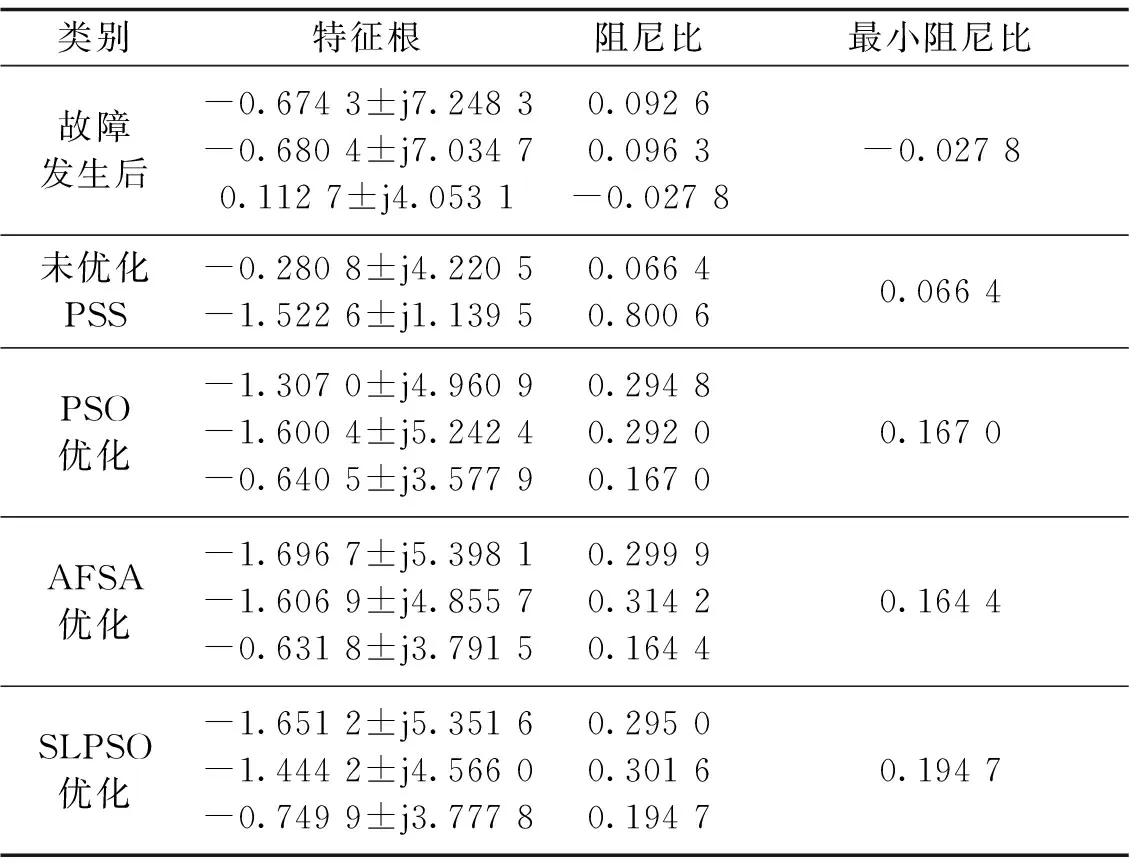
表4 各方法优化PSS后系统的特征根及阻尼比Tab.4 Characteristic root and damping ratio of system after designing PSS by different methods

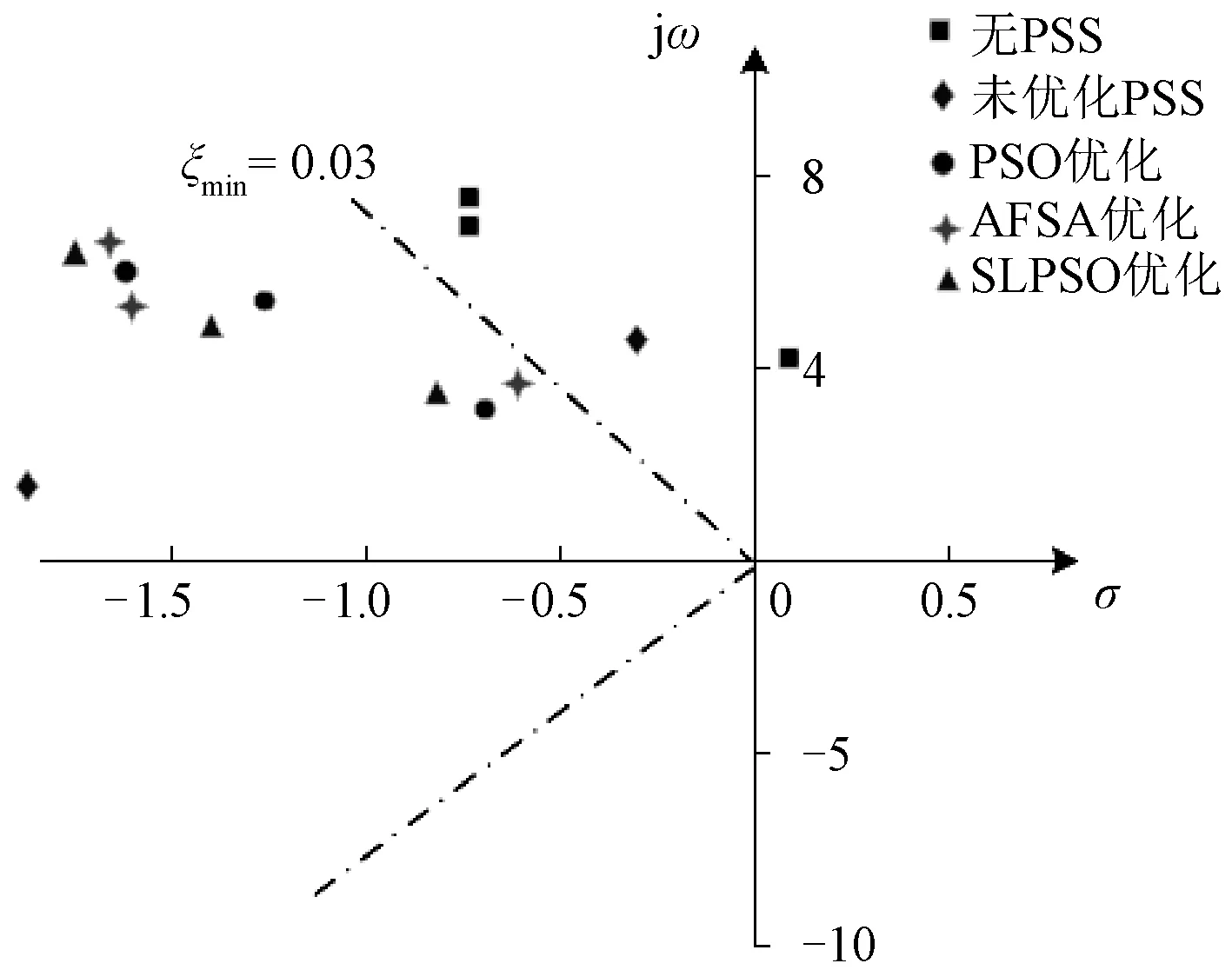
图13 机电模式特征根分布图(大干扰)Fig.13 Characteristic roots distribution chart of electromechanical mode

7 结论

(1)本文提出将SLPSO算法应用于多机系统PSS参数的优化整定问题中，其目的在于更好地抑制电力系统低频振荡并增强其动态稳定性能；并以四机两区系统为例，在系统受到扰动的情况下采用PSS对低频振荡加以抑制。

(2)对于PSS参数优化对象主要是对传统且结构固定的超前-滞后型PSS进行参数的优化整定，整定参数的目的在于使多机系统的弱阻尼振荡模式得到一定程度的增强。

(3)通过仿真实验，与未安装PSS、安装PSS但未优化PSS参数以及采用多种算法对PSS参数进行优化等多种情况加以对比分析，分析系统两区域之间联络线有功功率振荡以及发电机的转速偏差等低频振荡状况，通过仿真结果验证了本文所提方法的有效性与优越性。