多模型分层融合的配用电系统用户数据识别

蔡 军， 谢 航， 吴高翔， 唐贤伦， 邹 密

(1. 重庆市复杂系统与仿生控制重点实验室(重庆邮电大学)， 重庆 400065； 2. 国网重庆市电力公司电力科学研究院， 重庆 401120)

1 引言

用户数据识别通过无监督学习获得的特征库与典型用电模式之间建立映射关系，从而快速挖掘新用户潜在的用电模态与规律，减少不必要的共性行为分析。该方法适应了大数据时代的发展，应用于业扩报装业务[1]、电力信息通信客服系统[2]、光伏板积灰状态识别[3]等领域。而随着智能电网理论与实践的推进，配用电管理系统的时空机理模型和用户数据识别问题日渐复杂[4-6]。多源用户的用电数据个体差异性较小、波动性强以及负荷数据的非线性和时序性，给配用电系统数据识别带来新挑战。

用电数据识别方法分为两类，分别是机器学习和深度学习模型。基于机器学习的代表模型有马尔可夫模型[7]、随机森林[8]和支持向量机[9]等。这类模型实时性好、鲁棒性强，但需要繁杂的数据分析和特征降维操作[10]。而深度学习模型凭借强大的自主学习能力，弥补传统机器学习方法的不足，提高了模型性能[10]，代表模型有堆叠自编码器、深度信念网络和卷积网络等。其中，深度信念网络通过逐层训练和微调，有效地实现特征提取与分类，但隐层单元的超参难调，模型易收敛于局部最优。堆叠自编码器与深层卷积神经网络的联结可在少量样本数据上增强特征提取能力，而海量电力数据的增长足以满足卷积神经网络的训练。此外，卷积神经网络外部可扩展的网络结构、内部卷积运算和反向传播算法赋予了该网络强大的数据挖掘能力。因此，卷积神经网络具有一定的数据识别前景。

近年来，卷积神经网络在图像识别方面取得了突破性进展，同时在电力系统领域研究[10-14]也正如火如荼。文献[10,11]分别构建多维度多通道的融合卷积网络和一维卷积网络对端到端的时序电力系统暂态稳定特征提取与分类；文献[12]构建故障分类和定位双支路的卷积神经网络对多端直流输电线路故障快速、精确地诊断；文献[13]以不同网络层数、激活函数以及池化方式的卷积神经网络对差异性较小的高压电缆缺陷识别；文献[14]用卷积神经网络对量化后的监控警告信息有效识别。以上研究通过纵向增加网络的深度和构建对称结构的融合网络可获得较优的识别效果，但数据特点没有配用电数据复杂，并且网络结构和融合方法仍有如下不足：①纵向堆叠深层网络会出现梯度消失的现象；②卷积核采用单一尺寸，不能提取到浅层特征包含的丰富空间信息；③多个全连接层不仅增加计算量，还易过拟合；④模型同等权重的融合可能得到的分类精度低于基模型。

由于配用电数据的复杂性、现有研究领域的卷积网络结构和融合方法的不足，本文提出并运用多模型分层融合的方法对配用电数据进行识别。具体方法如下：首先，设计横向扩展的递归差分卷积网络对多源用户数据特征提取，使浅层信息融合时，防止梯度弥散；其次，采用改进自适应余弦学习率优化算法进行训练，保存最优模型；最后，对多模型分层加权融合，以阈值区间划分层级，通过新定义混淆矩阵的错误样本数确定权值，弥补了单一分类器分类效果不够理想的缺点。通过对配电系统的用户数据有效识别，有助于提高用户的用电效率与质量，保证电网的安全性与经济性。

2 多模型分层融合方法识别

2.1 递归差分卷积网络的卷积层构建

卷积神经网络(Convolutional Neural Network，CNN)可自主学习输入数据特征，避免了人工获取特征量带来的局限性和复杂性，简化了识别过程[15]，然而在众多电力数据研究中很少从卷积层横向扩展网络结构，所以本文以设计一维递归差分卷积神经网络为研究对象。

2.1.1 多尺度卷积模块联结

卷积层是卷积网络组成部分之一，主要通过一个小的权值矩阵即卷积核在输入数据上进行“滑动”，使卷积核内的元素与区域性特征线性运算。但实际的数据不全是线性的，为了增强网络的泛化性，使用激活函数。具体的卷积计算表达式如下：

(1)

式中，x为输入层；y为n×m的输出矩阵；I为卷积核的尺寸；wgh为g×h的卷积核；b为偏置；f为激活函数，常用的非线性激活函数有Sigmoid、ReLU、Tanh等。

由式(1)知，固定尺寸的卷积核受到感受野大小限制，无法捕捉到浅层特征包含的丰富空间信息。利用多尺度卷积核提取不同感受野的特征，再将其融合，有助于深入挖掘特征之间的空间局部相关性，提高分类精度。多尺度卷积模块联结如图1所示。

图1 多尺度卷积模块Fig.1 Multi-scale convolution module

2.1.2 递归差分卷积模块

深度学习中，随着网络堆叠梯度消失的现象越明显，网络识别的准确率先上升接着饱和，最后下降，模型的误差也会增大。为解决此问题，何凯明等人[16]提出残差模块，在浅层的网络叠加恒等映射[17]，即y=x。将前一层的输出传到后面，使原始所学的函数F(x)转化成H(x)=F(x)+x。

基于多尺度卷积与残差的思想，本文采用层层递归式的差分卷积，如图2所示。

注：conv3表示一维卷积核尺寸为3；Maxpool3表示最大池化层尺寸为3。图2 递归差分模块Fig.2 Recursive difference module

第一层：由于数据特征的时序性，以门控循环单元的时间分布(Time Distribute，TD)层作为第一层的主支路，将输入数据独立作用到时间片上，每个时间步对应一个输出；然后利用卷积神经网络的平移不变性，将多尺度卷积核提取的特征进行拼接，得到近端拼接特征图。此时多尺度卷积块不仅是残差块，还是第一层的辅支路。

第二层：将上一层的输出串联尺寸为3的卷积核作为下一层的残差块，用一个较大卷积核提取融合后的特征，有助于剥离原始数据单一的关系，挖掘不同信息之间的关联性。这样不免损失部分原始信息，为保留原始数据结构又提高数据的非线性特性，以尺寸为1卷积核对输入数据进行卷积。

为了防止设计的差分网络过拟合，每个卷积层增加了批归一化层、L2正则化对各层权值矩阵进行约束[11]。这种层层递归的结构，不仅提高了各级卷积利用率，使所提取的空间特征更加细致，同时使网络结构更加紧凑[18]。

2.2 递归差分卷积网络

设计的一维递归差分卷积网络，如图3所示。数据输入到卷积层进行特征提取；经过最大池化层缩小特征图的尺寸，降低过拟合的风险[19]；然后利用全局平均池化层(Global Average Pooling layer，GAP)代替平坦层和全连接层，直接对整张特征图求平均，以平均值作为属于某个类别的置信区间；最后输入Softmax中返回样本在各个类别的概率，以最大概率对应的类别作为最终结果。

图3 递归差分卷积网络Fig.3 Recursive differential convolutional network

对于卷积神经网络，引入GAP不仅可以代替虚线中两层的作用，使网络结构更加简洁，还可以减少全连接层带来的较大计算量。

2.3 改进卷积网络的训练算法

在网络结构设计完成后，通过最小化交叉熵损失函数训练网络，确定CNN模型。

2.3.1 自适应学习率优化算法

CNN的训练常用随机梯度下降算法(Stochastic Gradient Descent algorithm，SGD)，该算法存在两个缺点：①噪声的引入使权值更新方向不一定正确。②Hessian矩阵病态，即迭代的梯度方向和整个最优梯度方向不一致，导致损失函数下降振荡大。因此引入自适应学习率优化算法，直接加入了梯度一阶矩估计和二阶矩估计修正当前随机梯度下降，加速收敛的速度。表达式如下:

(2)

2.3.2 改进自适应学习率优化算法

由2.3.1节可知，学习率较小，收敛速度慢，学习率较大，易错过局部最小值[20]。为平衡这种矛盾，文献[20,21]分别提出K阶多项式衰减和余弦快照算法，本文基于以上思想，采用部分多项式与快照余弦的融合。表达式如下：

(3)

(4)

式中，η0为初始学习率；T为模型总的批量处理的次数；C为学习率循环退火次数，对应模型收敛到局部最优解的个数；K为K阶因子；mod为求余函数。

2.4 模型分层加权融合方法

2.4.1 传统加权融合方法

传统模型加权融合[22,23]方法原理：依据不同模型错分样本不完全重叠的特性，通过混淆矩阵中错误样本数确定权值，从而弥补单模型分类的适应度缺陷。

在融合方法中，常选取分类精度高的模型作为基模型，以正类样本预测为负类样本的数量越小，所占权重越大的思想确定权重，可获得分类精度高于最优单模型。当基模型分类精度均大于99%，即对正类样本分类正确的概率为0.6～0.9，负类样本预测正确的概率不超过0.5/(类别数-1)时，传统融合方法很难在最优分类的基础上进一步提高，同时还会出现分类错误的样本数转移现象。而这种现象对于用户用电行为的分类是很不利的，因为每类用户分类直接影响着营销方案的实施。若分类错误的用户用电量在该区域总电量占比很大，必会影响日后用户的用电习惯与电网效益。

2.4.2 分层加权融合方法

基于传统融合方法在用电数据识别的不足，本文引入不同层级的分类模型进行加权融合。

融合方法的原理：通过分类精度阈值对基模型划分层级，新定义混淆矩阵的错误样本数确定权值。其中基模型不再仅限于分类性能优良的单模型，权值确定不仅单方面考虑某类别预测错误的样本数，还包括负类预测为正类的样本数。该方法充分利用各分类器对某类别分类正确的潜力，使模型分类精度在最优基模型的基础上进一步提高。

分层加权融合方法的步骤如下：

(1)各分类器经过Softmax得到s行j列的概率矩阵(Xd)s×j(d=1,2，…，s)，其中Xd为第d行的样本，s为总样本数，j为类别数。

(2)以αl对分类器划分层级。每两个分类器分类精度差值在某一阈值区间，分类器划分为同一层级。表达式如下：

αl=[α1,α2,…,αs]

(5)

(6)

式中，cl为第l层分类器的验证集精度。

(7)

(8)

(9)

(10)

(11)

(12)

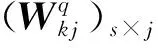
2.4.3 融合方法对比

为说明融合方法的优越性，采用2种方法进行对比。

方法1：基于文献[21]的思想，将分类精度高且相近的分类器进行加权融合，权值由新定义的错误样本数确定。

方法2：采用2.4.1传统融合方法，其中错误样本数确定权值的表达式如下：

(13)

2.5 识别方法流程图

本文流程图如4所示。首先将训练集分别输入第一层卷积神经网络与第二层机器学习模型中进行训练，其中第一层模型通过改进自适应学习率优化算法更新参数，第二层模型通过下采样平衡样本类别；然后将验证集数据输入已训练好的基模型中，用于模型类别权值的确定；最后通过两层模型对测试集类别预测值进行加权组合，输出最大概率对应的类别。

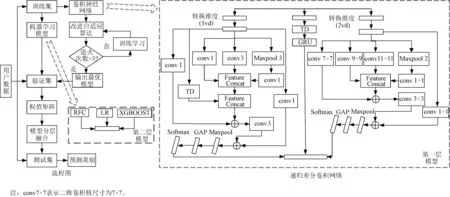
图4 识别方法流程图Fig.4 Identification method flowchart

各基模型说明：

第一层模型：一维递归差分卷积神经网络(One-dimensional Recursive Differential Convolutional Neural Network，1RD-CNN)、二维递归差分卷积神经网络(Two-dimensional Recursive Differential Convolutional Neural Network，2RD-CNN)和门控循环单元(Gated Recurrent Unit，GRU)。第二层模型：随机森林(Random Forest Classifier，RFC)、逻辑回归(Logistic Regression，LR)、极限梯度提升树(eXtreme Gradient BOOSTing，XGBOOST)。

2.6 测评指标

算法性能的评价指标为准确率ACC、召回率Rec、精确率Pre、F1值。公式如下：

(14)

(15)

(16)

(17)

式中，Ts为正类预测为正类的样本数；Fs为正类预测为负类的样本数；Tus为负类预测为负类的样本数；Fus为负类预测为正类的样本数。

3 算例分析

3.1 特征选取

数据采集于重庆市某地区2019/10～2020/9的20个行业。每个样本数据包括一日的有功负荷24整点值、无功负荷24整点值、24整点电量以及用户总容量。根据表1构建特征，其中N为一天采集的点数；M为一个月的天数；SN为额定容量；P、Q分别为有功功率与无功功率；Pmax、Pmin为最大、最小负荷；Pmean为负荷均值；E尖、E峰、E平、E谷为尖峰平谷各个时期的电量；E总为尖峰平谷时期的总电量。

表1 特征指标选取Tab.1 Feature index selection

3.2 特征库构建

根据3.1节计算得到106 738样本，以模糊C均值聚类算法构建4类别的特征库，每类用电模式分布见表2。

表2 用电模式分布Tab.2 Distribution of electricity consumption patterns

3.3 实验环境设置

实验环境为：框架Tensorflow、Keras；编程语言Python3.7；处理器CPU:i7-11800，GPU 3050TI。

3.4 数据集划分与模型参数设置

输入的数据按8∶1∶1的比例划分为训练集/验证集/测试集，各子集通过均匀随机抽样从总样本集中取出，保证各类别样本/总样本的比例在训练集、验证集和测试集中一致。多模型融合方法的第一层参数设置见表3、表4、表5，其中S表示填充。

表3 1RD-CNN参数设置Tab.3 1RD-CNN parameter settings

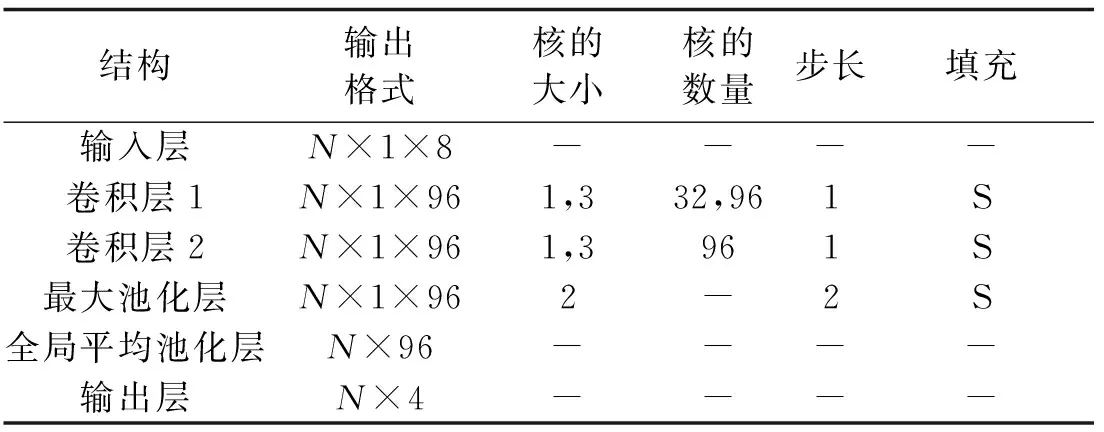
表4 2RD-CNN参数设置Tab.4 2RD-CNN parameter settings

表5 GRU参数设置Tab.5 GRU parameter settings

3.5 学习率优化算法对比

由于1RD-CNN与2RD-CNN模型设置参数一致，本文以1RD-CNN为例，经过训练获得学习曲线精度对比如图5所示。其中迭代轮数为120,每轮小批量处理样本数为100，L2正则化惩罚系数为0.01，激活函数为tanh，初始学习率为0.01，β1=0.95,β2=0.99，学习率循环退火次数为3。快照余弦与改进算法的学习率分布、相同学习率区间内首次退火的准确率曲线分别如图5(a)、图5(b)所示。为验证改进算法的可信度，同时排除初始随机梯度方向带来的偶然性，进行了3次训练，保留每次最高准确率，如图5(c)所示。虚线左、右边分别代表快照余弦与改进算法的模型分类准确率。

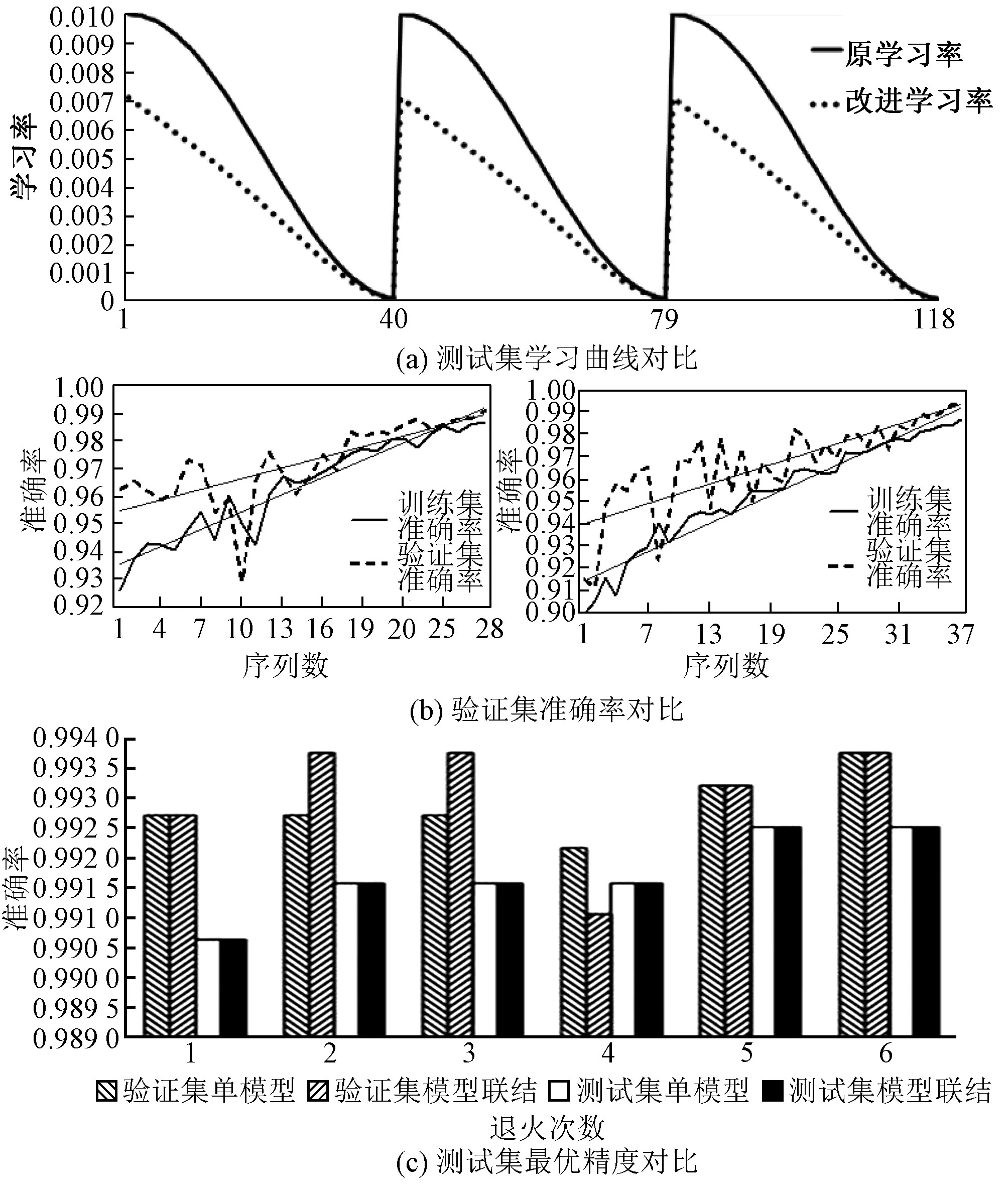
图5 学习曲线与精度对比Fig.5 Comparison of learning curve and accuracy

由图5(a)、图5(b)可知，两种算法初始学习率相同，但改进的算法学习率起点较小，下降速度相对较缓。当学习率小于0.007，原算法训练集与验证集的准确率均达到99.8%时，模型饱和，之后出现过拟合的现象。而改进算法准确率超过99% 时，仍有上升的空间。说明动态学习率可提升网络分类性能。

由图5(c)可知，多次运行模型的分类精度最终趋于稳定值。对于验证集，两种算法最优精度均是99.35%，对于测试集，改进后的算法精度提高了0.1%。验证了改进算法的有效性。

3.6 验证分层加权融合方法的有效性

为验证融合方法中模型分层和权值确定的有效性，进行了三组模型对比，如图6所示。其中验证集与测试集的样本数均为1 067，4类别样本数分别为344、196、209、319；组合一与组合二的第一层权值相同，两层级的阈值α1=0.001，α2=0.01；纵坐标为实际类别，横坐标为预测的类别。各模型组合如下：

图6 模型组合对比Fig.6 Model combination comparison

模型组合一(加权)：

1RD-CNN+2RD-CNN

模型组合二(分层加权)：

1RD-CNN+2RD-CNN+LR+XGBOOST

模型组合三(分层加权)：

1RD-CNN+2RD-CNN+GRU+LR+RFC+XGBOOST

由图6(a)、图6(b)可知，框出区域的权值均与传统确定的权值不一样。如类别3，图6(a)中LR与XGBOOST模型的新定义错误样本数比为16∶8，确定的权值为0.33∶0.67，XGBOOST模型所占的权重大，而传统方法中正类别预测错误的样本数为0∶4，LR模型所占的权重大；图6(b)中LR、RFC和XGBOOST模型的新定义错误样本数比值为16∶14∶8，确定的权值为0.21∶0.37∶0.42，XGBOOST模型所占的权重大，传统方法确定的权重比值为1∶0∶0，LR模型所占的权重最大。

由图6(c)可知，3种组合模型准确率均很高，但仍存在细微差别。①组合一和组合二相同的模型处于同一层级具有相等的权值，但分层的组合模型二比组合一预测实际类别0的错误样本数少一个，说明分层融合方法的有效性。②组合三增加了两个分类性能低于同层级的模型，但预测实际类别2的错误样本数比组合二少一个，说明分层加权融合方法不仅在正类样本预测正确的基础上，通过增加模型的个数，进一步提高分类准确率，还充分利用各分类器对某类别分类正确的潜力，避免出现预测类别错误对应的样本数转移现象。

3.7 模型识别性能对比分析

为说明本文识别方法的优越性，从网络结构和模型融合方法进行比较，具体见表6。

表6 模型性能对比Tab.6 Model performance comparison

选取对比的网络是：文献[10]采用传统的两层卷积池化网络，文献[11]采用深度大于二的卷积池化网络，RD-CNN[18]是两层递归差分网络，以上网络均没有考虑多尺度卷积对特征提取和动态学习率对分类精度的影响。

以2.4.3节融合方法进行对比，方法1采用分类精度高且相近的2种模型，分别为1RD-CNN+2RD-CNN，传统方法与该方法的分类结果一致；方法2与本文融合方法均采用6种基模型，分别为1RD-CNN+2RD-CNN+GRU+LR+RFC+XGBOOST。

由表6可知：①对于网络结构，本文设计的递归差分卷积网络识别性能均高于其他3种卷积网络，其中1RD-CNN分类性能最优，比传统卷积网络CNN[10]准确率提高0.35%，说明多尺度模型联结与递归结构组合的网络可以挖掘数据深层的特征，而RD-CNN[18]比CNN[11]的分类性能低，说明对于用户数据采用固定尺寸卷积核作为差分块的卷积网络，其网络性能比不上深层的卷积池化网络。②对于融合方法，方法1与1RD-CNN的分类结果一致，说明少量分类精度高的基模型融合后的分类性能很难进一步提高；本文方法比方法1准确率提高0.18%，说明增加分类精度低的模型进行分层加权融合可以突破最优单模型分类瓶颈；此外，在相同基模型下，本文方法比方法2准确率高0.47%，说明分层以及新定义错误样本数确定权值的方法优于传统加权融合方法。

由网络结构和融合方法对用户数据识别性能分析可知，多尺度递归差分卷积网络很好地学习了数据深层特征，分层加权融合方法可以在基模型获得较高识别率的基础上，进一步提高识别性能。

4 结论

对于配电系统用户数据的识别，本文提出多模型分层融合方法。通过实验分析可以得到以下结论：

(1)相较于固定尺寸卷积核的深层网络结构，利用多尺度模块联结作为差分块；全局平均池化层代替平坦层与全连接层；动态自适应学习率对网络进行训练，更能提取丰富的空间信息，从而获得更优的分类效果。

(2)相比于传统加权融合法，通过分层和新定义错误样本数确定权值，不仅有效克服了各基模型融合后的适应度缺陷，提高融合模型的分类性能，还充分挖掘出各分类器对某类别分类正确的潜力，避免出现预测类别错误对应的样本数转移现象。