无线充电系统实际Litz线绕平面线圈高频电阻分析与计算

薄 强， 王丽芳， 张玉旺， 郭彦杰， 张 云

(1.中国科学院电工研究所， 北京 100190； 2.中国科学院电力电子与电气驱动重点实验室， 北京 100190； 3.中国科学院大学， 北京 100049； 4.清华大学电机工程与应用电子技术系， 北京 100084)

1 引言

无线充电技术在电动汽车、医疗、电子产品等领域的研究与应用越来越引起关注[1-4]。其中，电动汽车无线充电系统的工作频率一般在几十或几百kHz，高频下实心导线趋肤效应、邻近效应严重，线圈损耗大，为降低线圈损耗提高系统效率，无线充电系统的线圈往往采用Litz 线绕制。Litz 线是由多股相互绝缘的细导线扭转缠绕而成，高频下各细导线上的电流分布较为平均，可以同时减弱趋肤效应和邻近效应的影响。发射线圈和接收线圈的电阻值对无线充电系统的传输效率有关键影响。Litz 线高频电阻的计算是无线充电系统线圈优化设计的基础。

Litz线的结构使得直接使用有限元仿真建模过于复杂，剖分网格的数目太多，计算规模十分庞大，浪费时间和计算资源。目前，已有相关文献对Litz线线圈高频电阻的计算进行研究。文献[5-7]通过解析计算消除空间扭转效应，并采用有限元或数值仿真模型进行计算；文献[8-10]针对利兹线的非理想特性和扭转结构，采用部分元件等效和有限元结合的方法对功率损耗进行了计算；文献[11,12]应用毕奥-萨伐尔定律对平面矩形螺旋线圈中的磁场进行解析计算，经过一系列数学推导后采用开尔文函数来进行利兹线高频电阻的计算；文献[12-14]将Litz线等效为具有复数电导率和复数磁导率的实心导线，然后代入有限元仿真模型进行计算；文献[15,16]引入宏观复数磁导率的概念来评估由于邻近效应引起的Litz线涡流损耗，并采用基于均匀化的有限元分析进行计算。但是，上述计算方法的适用对象均为理想Litz线，实际工程应用中的Litz线测量得到的电阻值均大于上述计算方法得到的电阻值。进一步地，对于实际Litz线，文献[17]通过对理想Litz线和平行束导线的电阻值进行线性拟合来计算实际Litz线的电阻值；文献[18]引入不均匀系数的概念，可以基于理想Litz线电阻值来计算实际Litz线电阻值。当系统中有多个线圈时，其他线圈产生的交变磁场会在待求解线圈中产生感应电阻，而对于双D(Double-D，DD)线圈，还需要考虑两个线圈之间的耦合感应电阻。但是文献[17,18]均没有考虑线圈之间电磁场的相互耦合作用对电阻值的影响，这会给实际Litz线电阻的准确计算带来误差。

本文针对电动汽车无线充电系统，提出一种无线充电系统实际Litz线平面线圈高频电阻的计算方法，以提高线圈高频电阻计算的准确性。所提计算方法不仅考虑了线圈自身结构参数对电阻值的影响，还考虑了不同线圈之间的电磁场相互耦合作用对电阻值的影响。最后，搭建实验平台并运用该方法计算平面矩形线圈和DD线圈的电阻值，结果表明，该计算方法在不同频率范围内得出的结果与实际测量结果吻合很好，验证了本文计算方法的有效性和可行性。所提计算方法可以对无线充电系统线圈的优化设计提供理论依据，避免线圈的重复绕制与测量，节省时间和成本。

2 Litz线空间结构分析

Litz线是由多股相互绝缘的单线绞合而成，其基本组成单位是单股漆包线。通过绞合，Litz线中所有单股线被自由排列，在Litz线的截面上单股线可能处于任意位置。图1为Litz线空间结构分布与相应单股线的结构。由于扭绞工艺的影响，实际工程应用中使用的均是非理想的Litz线，如图1(a)所示为实际Litz线，其空间结构介于理想Litz线和平行束导线之间，因此其电阻值也介于理想Litz线和平行束导线之间。图1(b)为理想Litz线的导线截面结构，其每一股单线均占据了导线截面上径向和方位角的每个位置，即每一股单线均占据了其他单线的所有位置，导致电流在每一股单线中均匀分布，理论上每一股单线的内阻均相等。图1(c)为平行束导线的导线截面结构，平行束导线的每一股单线位置均保持固定不变，单线之间不会互相交换位置，每一股单线的内阻将根据单线在Litz线中的位置不同而发生变化。

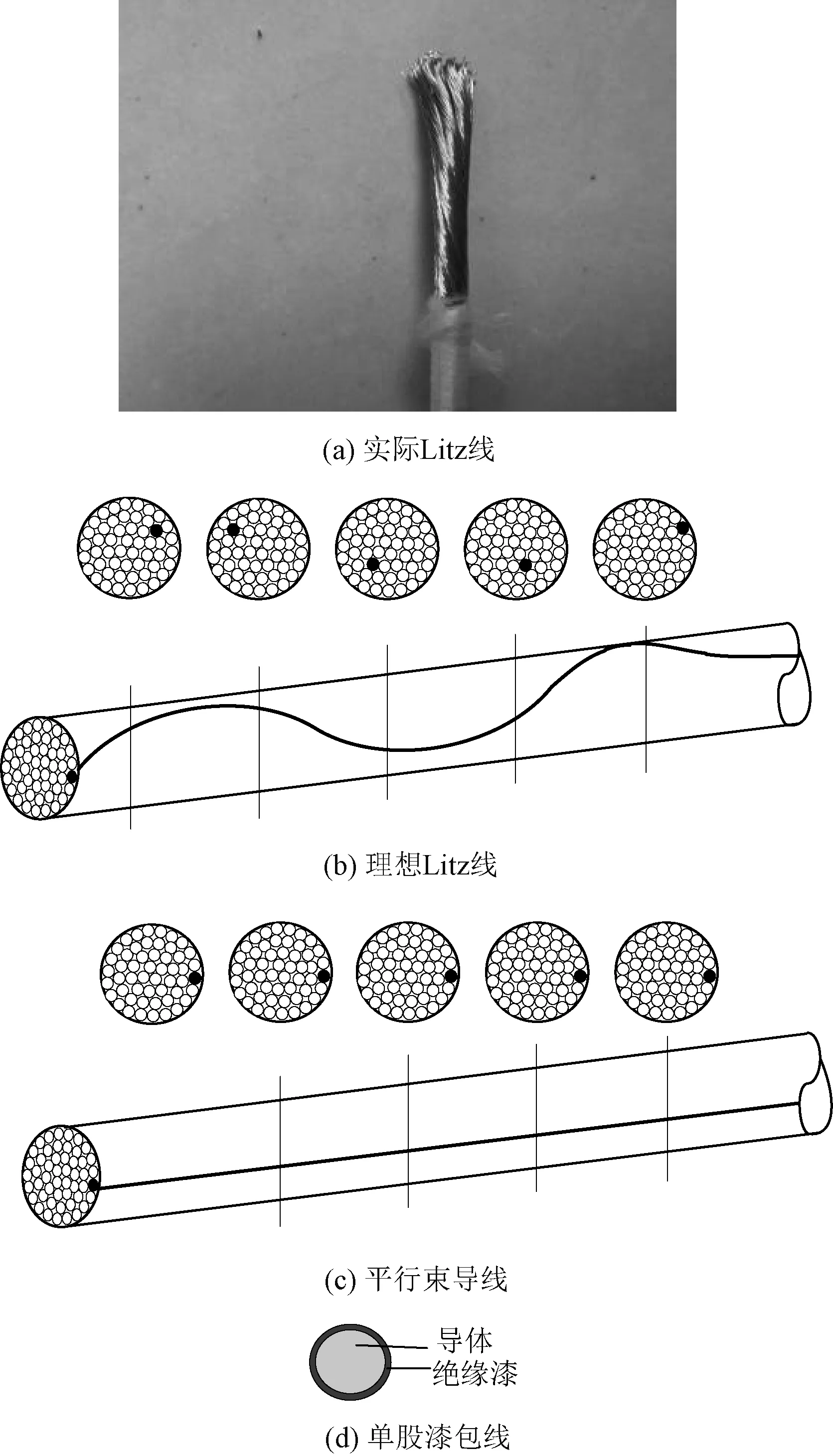
图1 Litz线空间结构分布图与单线结构图Fig.1 Spatial distribution of Litz wire and structure of a strand

Litz线绕制线圈的损耗由两部分组成[19,20]，与损耗相关的电阻值R可以表示为：

R=Rcond+Rprox=Rcond+Rint+Rturn+Rcoup

(1)

式中,Rcond为导通电阻，导通损耗包括线圈的直流损耗和由趋肤效应引起的涡流损耗;Rprox为邻近电阻，邻近损耗是由邻近效应引起的涡流损耗。邻近电阻由三部分组成，Rint为内部感应电阻，Litz线内单线的交变磁场将会在邻近的单线中产生涡流损耗，称之为内部感应损耗；Rturn为匝间感应电阻，线圈中线匝产生的交变磁场会在邻近线匝中产生涡流损耗，称之为匝间感应损耗；Rcoup为耦合感应电阻，外部其他线圈产生的交变磁场会在该线圈中产生涡流损耗，称之为耦合感应损耗。

Rcond和Rint只和Litz线本身的结构参数、长度、工作频率有关，和线圈绕制的结构参数无关，可以定义两者之和为Litz线的本征电阻Ric，如式(2)所示；Rturn、Rcoup和线圈绕制的结构参数相关，是由该线圈其他线匝和外部其他线圈产生的交变磁场引起的涡流损耗，可以定义两者之和为Litz线绕线圈的外部感应电阻Rext，如式(3)所示。

Ric=Rcond+Rint

(2)

Rext=Rturn+Rcoup

(3)

3 Litz线高频电阻组成与影响因素

通过对Litz线空间结构的分析可知，Litz线绕制线圈的高频电阻组成可分为Litz线的本征电阻和Litz线绕线圈的外部感应电阻，本节对这两部分电阻的计算方法进行分析。

3.1 本征电阻

3.1.1 理想Litz线的本征电阻

对于理想Litz线，单位长度的导通电阻可以表示为：

(4)

式中，ξ为与趋肤深度δ相关的量，m-1；n0为组成Litz线的单线的匝数；r0为组成Litz线单线的标称半径(不包括绝缘漆厚度)，m；σ为导线的电导率，铜的电导率为5.8×107S/m；Φcond(ξr0)为与ξ、r0有关的中间变量，其表达式为：

(5)

(6)

式中，μ为导线的磁导率，H/m;ω为角频率，rad/s; ber,bei分别为第一类0阶开尔文函数的实部和虚部；ber′,bei′分别为第一类0阶开尔文函数的导数的实部和虚部。

对于理想Litz线，单位长度的内部感应电阻可以表示为：

(7)

式中,rc为Litz线没有包覆层时的外径，由于Litz线天然的柔韧性、弯曲的半径等都会影响外径的测量结果，因此外径是依据测量的平均值来进行近似测定；Φind(ξr0)为与ξ、r0有关的中间变量，其表达式为：

(8)

式中，ber2，bei2分别为第一类2阶开尔文函数的实部和虚部。

综上所述，理想Litz线单位长度的本征电阻可以表示为：

Rid,ic,ul=Rid,cond,ul+Rid,int,ul

(9)

3.1.2 平行束导线的本征电阻

在平行束导线中，单线中的电流将根据单线在Litz线中的位置发生变化，每一股单线的内阻均不相等。平行束导线的电流分布和损耗与具有相同外径的实心导线的电流分布和损耗相当，但是实心导线的电导率需要做相应调整，电导率等效依据为使平行束导线和等效实心导线的直流电阻相等。

因此，在求解平行束导线的固有电阻时，可以将平行束导线等效为半径为re、电导率为σe的实心导线。等效半径和等效电导率可以分别表示为：

re=rc

(10)

(11)

等效实心导线为单根导线，因此没有内部感应损耗，其单位长度的导通电阻即为其单位长度的本征电阻。所以平行束导线单位长度的本征电阻Rpar，ic，ul等于等效实心导线单位长度的导通电阻，如下所示：

(12)

其中

(13)

(14)

式中,ξe为与等效实心导线趋肤深度δe相关的量。

3.2 外部感应电阻

相比于线圈尺寸，Litz线线径很小，无论是理想Litz线还是平行束导线，由外部磁场引起的涡流损耗几乎相等，因此在计算外部感应电阻时，可以忽略线圈的内部结构，将实际Litz线视为电流均匀分布的实心导线。

3.2.1 匝间感应电阻

单位长度的匝间感应电阻均可表示为：

(15)

式中，H2为当线圈中通过1 A幅值的正弦电流时，在导线横截面处按照面积的平均所产生的平方磁场强度。

由于不同位置的导线截面平方磁场强度的面平均值不相等，因此，计算匝间感应电阻时，需要对式(15)进行沿导线方向的线积分，从而线圈的匝间感应电阻为：

今年以来，降低增值税税率、扩大增值税留抵退税范围、放宽享受减半征收企业所得税优惠的小型微利企业标准、提高企业研发费用税前加计扣除比例、个税改革等一系列减税降负措施先后落地。谈到税收优惠政策落实，昆药集团股份有限公司财务人员张佳佳说：“我们每年的研发投入在1个亿左右，享受研发费用加计扣除政策有效缓解了资金压力，加大了企业研发的信心。”

(16)

式中，l0为线圈导线的长度；Vcoil为线圈导线的体积；Scoil为线圈导线的截面积；H0为线圈中通过1 A幅值的正弦电流时导线内的磁场强度，对平方磁场强度进行体积分后进一步计算即可得到匝间感应电阻。

线圈的匝间感应损耗可以表示为：

(17)

式中，I0为线圈内通过的电流幅值。

3.2.2 耦合感应电阻

当无线充电系统中有多个线圈时，其他线圈产生的交变磁场会在待求解的线圈中产生涡流损耗。假设除了待求解的线圈外，系统中还有N个其他线圈，设为线圈i,则待求解线圈和线圈i的耦合感应电阻可以表示为：

(18)

式中，Hi为线圈i中通过1 A电流、其他N个线圈中通过0 A电流时，待求解线圈内的磁场强度。

相应地，待求解线圈的所有耦合感应损耗可以表示为：

(19)

式中，I0为待求解线圈内通过的电流幅值；Ii为线圈i内通过的电流幅值。

当待求解线圈和其他线圈i中的电流幅值相等时，待求解线圈的耦合感应电阻为：

(20)

在无线充电系统中，接收线圈和整流器之间连接阻抗匹配网络，其作用是将等效负载匹配至呈纯阻性，提高无线充电系统的传输能力。设发射线圈中的电流为Ip，接收线圈中的电流为Is，发射线圈和接收线圈之间的互感为M，等效负载为Req，则可以得到：

(21)

由式(21)可知，发射线圈和接收线圈中的电流相位差为90°，因此式(20)中磁场强度H0和Hi相位差为90°，发射和接收线圈的耦合感应电阻为零。

4 实际Litz线绕平面线圈高频电阻计算

由于实际应用中的Litz线空间结构介于理想Litz线和平行束导线之间，因此，为了在理想Litz线和平行束导线的本征电阻求解基础上求出实际Litz线的本征电阻，可以对电阻Rid,ic,ul和Rpar,ic,ul进行线性拟合来表示实际Litz线单位长度的本征电阻Rλ, ic, ul，如下式所示：

Rλ,ic,ul=λRid,ic,ul+(1-λ)Rpar,ic,ul

(22)

式中，λ为实际Litz线的质量因数，只与Litz线导线自身结构参数有关，与外部的磁场等无关，λ=1表示质量最好的理想Litz线，λ=0表示平行束导线。

另外，为了计算DD线圈的外部感应电阻，可以将DD线圈的两个平面矩形线圈分别进行计算，在计算过程中，需要考虑两个线圈之间的耦合感应电阻。两个线圈中的电流方向相反、幅值相等，因此可以先计算其中一个线圈的匝间感应电阻，然后计算另一个线圈与该线圈的耦合感应电阻，匝间感应电阻和耦合感应电阻相加后乘以2即可得到DD线圈的外部感应电阻。DD线圈中的两个平面矩形线圈电流相位差为180°，所以，在待求解线圈中对应的H0和Hi相位差为0°，代入式(20)即可计算两个矩形平面线圈的感应耦合电阻，进而得到DD线圈的电阻。

图2(a)和图2(b)分别为用于磁场强度计算的平面矩形线圈和DD线圈模型。无论是平面矩形线圈还是DD线圈的磁场强度计算，在分析第i个线圈边AB处的磁场时，均可做如下假设[11,21]：

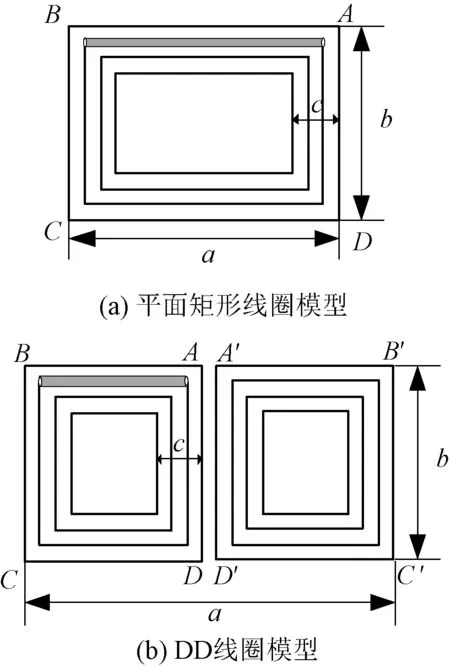
图2 计算磁场强度的线圈模型Fig.2 Coil model for magnetic field calculation

(1)AB边垂直于轴向，有横截面积，电流均匀分布于该横截面，需要分别计算导线内各点的磁场强度并进行体积分。

(2) 第i个线圈的其余3条边及其他线圈所有的边是没有横截面积的，所有的电流都集中于中心线，即视为所谓的线电流。

基于上述假设的计算结果可在保证精度的同时大大减少计算时间。可以采用文献[11, 21]的解析方法或有限元仿真软件来计算磁场强度。

综上所述，可得到实际Litz线绕制线圈的高频电阻为：

(23)

式中，l为绕制线圈的Litz线的总长度。

通过测量实际Litz线绕制线圈不同频率对应的电阻值，同时计算式(23)中各个变量的值，即可通过拟合得到λ值。由于λ值只和导线自身参数相关，所以得到的λ值可以用于同类Litz线绕制的其他线圈的电阻计算。

5 实验验证

为了验证所提出的实际Litz线绕制线圈高频电阻计算方法的正确性，采用两种不同类型的Litz线来绕制平面矩形线圈和DD线圈，并分别对其高频电阻值进行实验测量，为了表述方便，可分别定义两类线圈为m类Litz线和n类Litz线。两种不同类型Litz线的结构参数见表1, 采用这两种Litz线绕制的五种不同线圈的形状参数见表2。其中，表2中DD线圈的匝数是指DD线圈中一个矩形线圈的匝数，a、b分别为线圈的长和宽，c为绕制线圈的Litz线的总宽度，其物理意义如图2(a)和图2(b)所示。

表1 Litz线的参数Tab.1 Parameters of Litz wire

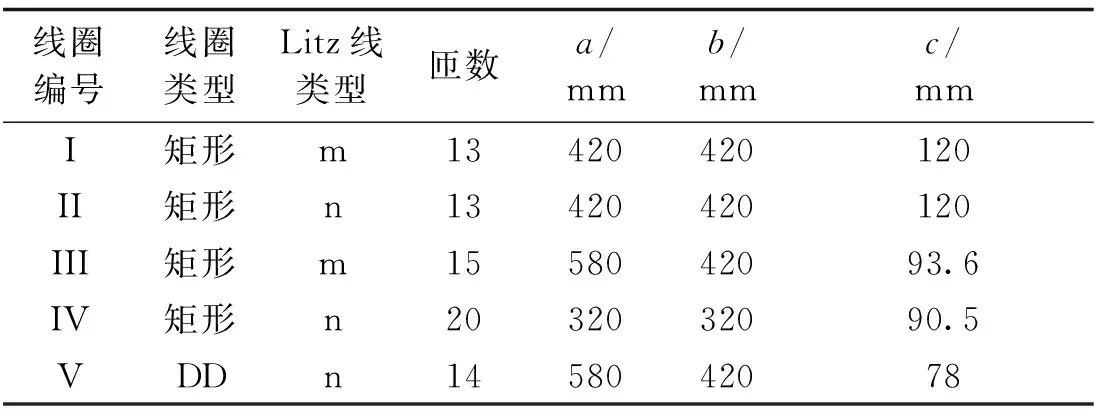
表2 线圈参数Tab.2 Parameters of coils

首先，分别采用m类和n类Litz线绕制了形状尺寸完全相同的平面矩形线圈I和平面矩形线圈II，线圈I和线圈II的结构分布如图3所示。采用LCR表(Agilent E4980A)分别测量线圈I和线圈II在不同频率(10～400 kHz)的电阻值，分别计算两个线圈对应的Rid,ic,ul、Rpar,ic,ul、l、Rext，代入式(23),通过最小二乘法拟合即可得到两类Litz线的质量因数。计算得到m类Litz线的质量因数为λm=0.656，n类Litz线的质量因数为λn=0.704。结合式(22)，可以分别得到m类Litz线和n类Litz线的单位长度本征电阻值，如图4(a)和图4(b)所示。

图3 线圈I与线圈Ⅱ空间结构分布Fig.3 Structures of coil I and coil Ⅱ

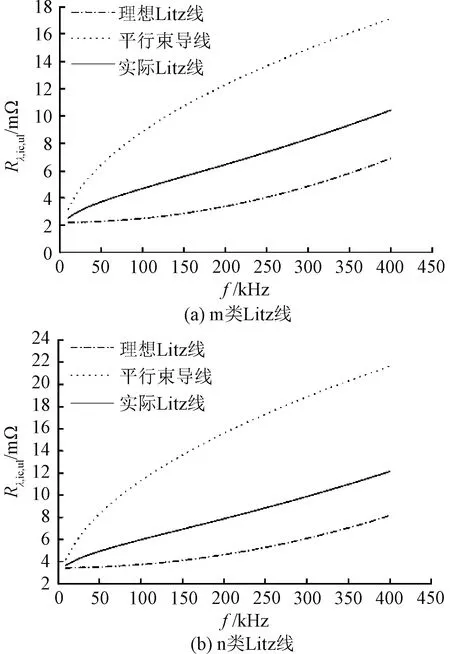
图4 Litz线单位长度的本征电阻Fig.4 Intrinsic resistance of Litz wire for per unit of length

其次，基于SAE J2954标准中的WPT1/Z2系统搭建了平面矩形线圈III和平面矩形线圈IV。其中，线圈III使用的是m类Litz线，线圈形状尺寸和WPT1/Z2中的发射端线圈相同；线圈IV使用的是n类Litz线，线圈形状尺寸和WPT1/Z2中的接收端线圈相同。Litz线绕制的线圈III和线圈IV如图5所示。

图5 Litz线绕制的平面矩形线圈Fig.5 Planar rectangular coils wound with Litz wire

再次，计算线圈导线内的磁场强度,结合式(23)即可计算线圈Ⅲ和线圈Ⅳ在不同频率下的电阻值。图6为Litz线绕制线圈Ⅲ和线圈Ⅳ的测量电阻和计算电阻对比图，可以看出，高频电阻的计算值和测量值有很大的吻合度。

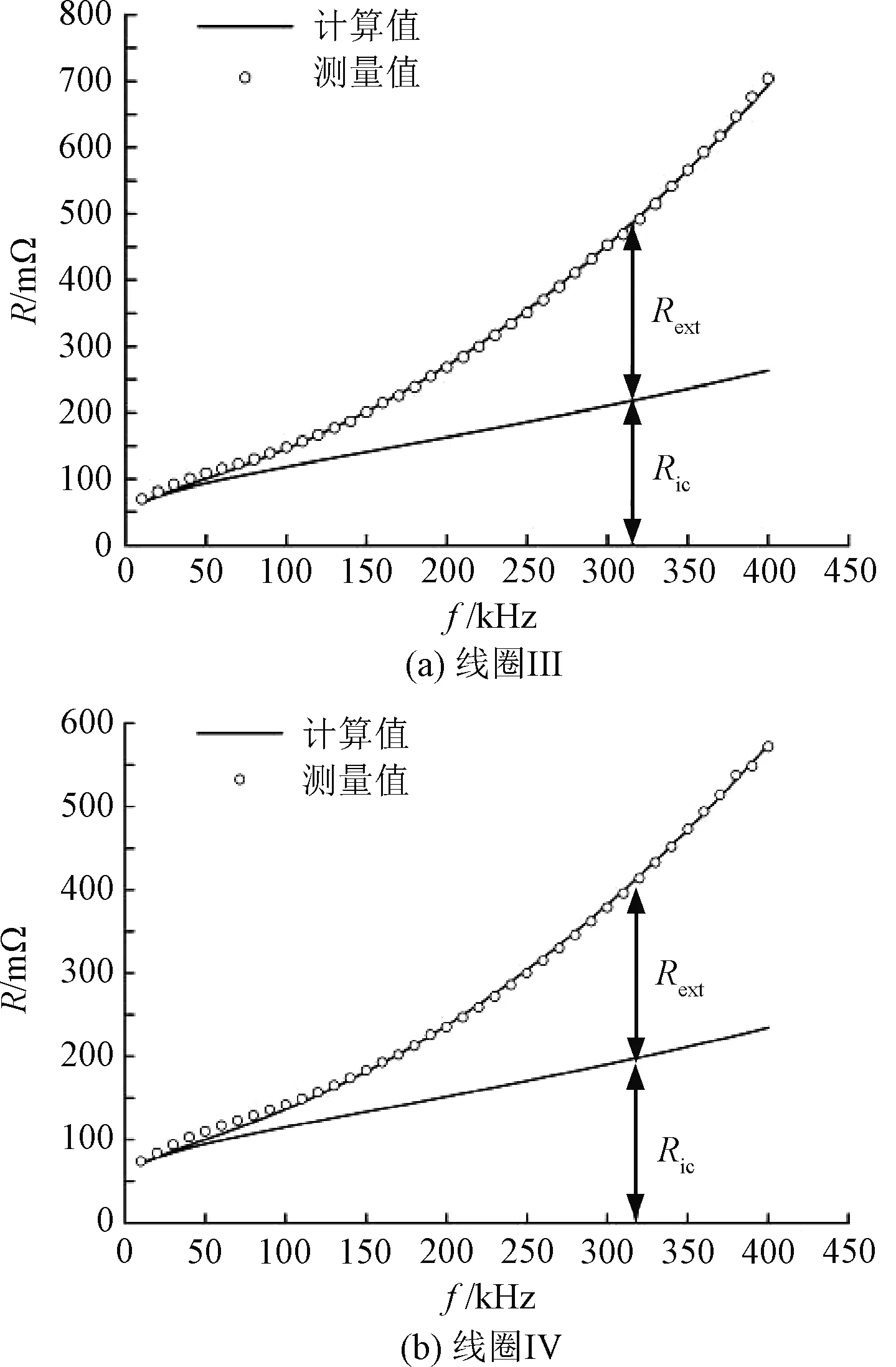
图6 Litz线绕制线圈高频电阻测量值和计算值Fig.6 Measured and calculated results of frequency-dependent resistance for Litz wire coils

最后，根据表2中的线圈尺寸参数，搭建DD线圈Ⅴ，如图7所示。其中，T2端子和T4端子连接在一起，DD线圈中两个矩形线圈的电流方向相反。计算对应的线圈导线内磁场强度，结合式(23)即可计算出DD线圈不同频率下的电阻值。将DD线圈高频电阻的计算值和实际测量值进行对比，如图8所示，可以看出高频电阻的计算值和测量值也有较高的吻合度，说明该方法也同样适用于DD线圈电阻值的计算。

图7 Litz线绕制的DD线圈ⅤFig.7 DD coil Ⅴ wound with Litz wire

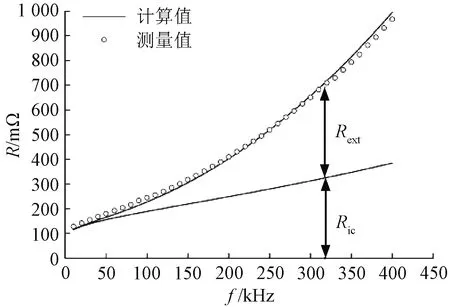
图8 线圈Ⅴ高频电阻测量值和计算值Fig.8 Measured and calculated results of frequency-dependent resistance for Litz wire coil V

6 结论

本文提出了实际Litz线绕平面矩形线圈和DD线圈电阻值的解析计算方法，且考虑了不同线圈之间电磁场的相互耦合作用对电阻的影响，结论包括：

(1)实际Litz线的电阻值介于理想Litz线和平行束导线之间，对理想Litz线和平行束导线的电阻进行拟合即可得到实际Litz线的电阻。

(2)相同规格的Litz线具有相同的质量因数，因此可以通过一组线圈得到的质量因数来预测相同规格Litz线绕制的其他平面矩形线圈和DD线圈的高频电阻值。

(3)在10～400 kHz的频率范围内，对于平面矩形线圈和DD线圈，所提计算方法得到的高频电阻计算值和实际实验测量值具有较高的吻合度。

线圈的高频电阻值对无线充电系统的传输效率有关键影响，为了避免重复的绕制线圈进行测量，可以直接采用本文方法来计算平面线圈电阻值，节省了时间和成本，可以为无线充电系统线圈的优化设计提供理论依据。