基于变结构补偿网络的WPT恒流/恒压充电系统

王德玉， 秘锡鸿， 傅超伟， 胡 挺， 赵清林

(燕山大学电气工程学院， 河北 秦皇岛 066004)

1 引言

随着国家十四五规划的提出，新能源汽车将迎来长足的发展[1-4]。无线电能传输(Wireless Power Transfer，WPT)技术应用于电动车辆充电不仅可以避免传统接触式充电因用电设备反复插拔摩擦造成的磨损、电火花以及输电线路老化带来的安全隐患[5]，还可以和自动驾驶技术相结合，进一步提高汽车系统的智能化以及自动化程度。目前，动力电池的性能是限制电动车辆推广的重要因素。电池的充电需求包括充电方式、充电结束电压、充电电流等。由于电池在充电过程中电压变化范围较大，电池等效电阻不断增大，因此宜采用先恒流再恒压的充电方式[6-8]，并尽量减少电流、电压波动。目前关于WPT系统恒流/恒压输出的研究大致分为两类：第一类采用闭环控制，通过改变直流母线电压[9]、逆变器移相角[10]或补偿电感值[11]来实现输出电流或电压恒定。这类方法都需要辅以实时的无线通信环节，根据误差信息和控制算法来调节被控量，增加了控制复杂程度。并且由于存在时延及通信可靠性问题，不适用于高频工作的WPT系统[12]；第二类是利用补偿网络的自身特性，通过改变补偿网络的结构或参数、调整工作频率点来实现系统的恒流或恒压输出。文献[13]采用双边LCC拓扑，通过在较窄的频率变化范围内调频，实现了恒流/恒压输出，但该方法未能在充电的全过程中维持零相位角(Zero Phase Angle，ZPA)状态，导致系统在恒压充电过程中无功损耗较多。文献[14]提出两种混合拓扑(S/P-S和S/P-P)用于电池恒流/恒压充电，但都需辅以三组切换开关来改变拓扑结构，提高了成本和控制复杂性。文献[15,16]分别改进了发射端补偿网络的参数或结构，达到优化系统输出特性的目的，但都需要配备无线通信环节。为了避免对实时通信的依赖，文献[17]提出一种接收端变结构的F-F/T复合拓扑网络，来满足电池恒流/恒压充电需求，然而该方法所用无源元件和辅助开关数量较多。文献[18]通过在接收端调整补偿参数来减少辅助开关的数量，但由于未能实现ZPA特性，系统无功损耗降低了整体效率。上述变结构控制，通常是利用辅助开关完成补偿结构或参数的改变，需要特别注意模式硬切换引起的能量冲击可能会造成功率器件的烧毁。文献[15-18]均未给出这一方面的进一步说明，而文献[19]针对这一典型问题分别提出了软件和硬件保护措施，但软件保护措施需要无线通信环节且增加了停机工序。而硬件保护措施则需要额外的开关和泄能电阻，增加了系统成本。

综上所述，变结构控制在实现恒流/恒压输出特性的同时，应尽量减少辅助开关的数量和切换暂态冲击引起的电应力，并最大程度降低系统无功损耗，这是目前该项技术面临的挑战。本文在双边LCC补偿网络基础上，研究一种接收端网络变结构拓扑，通过附加一个补偿电容和两组双向开关，实现不同补偿结构配置，从而在改变系统输出特性的同时，减少无功损耗。该工作简化了系统结构和控制难度，使系统摆脱了对通信的依赖。所设计的切换开关控制策略能够避免暂态冲击，提高了系统运行可靠性，对推动WPT用于电动车辆动力电池的充电具有积极意义。

2 WPT变结构补偿原理分析

图1为本文提出的WPT系统LCC-LCC/S变结构补偿网络原理图。其中，Uin为输入直流源；uo和io分别为动力电池等效负载电阻Ro端电压和电流；Co为输出滤波电容；uAB为Q1～Q4逆变桥产生的高频方波电压；ip和is分别为发射和接收线圈电流；VD1～VD4构成整流电路，其输入电压为uab；iL1和iL2分别为发射端串联补偿电感L1和接收端串联补偿电感L2的电流；iC2为接收端并联补偿电容C2的电流；Lp为发射线圈自感；Ls为接收线圈自感；M为松耦合变压器的互感；C1和Cp分别为发射端并联和串联补偿电容；Cs1和Cs2分别为接收端串联补偿电容。

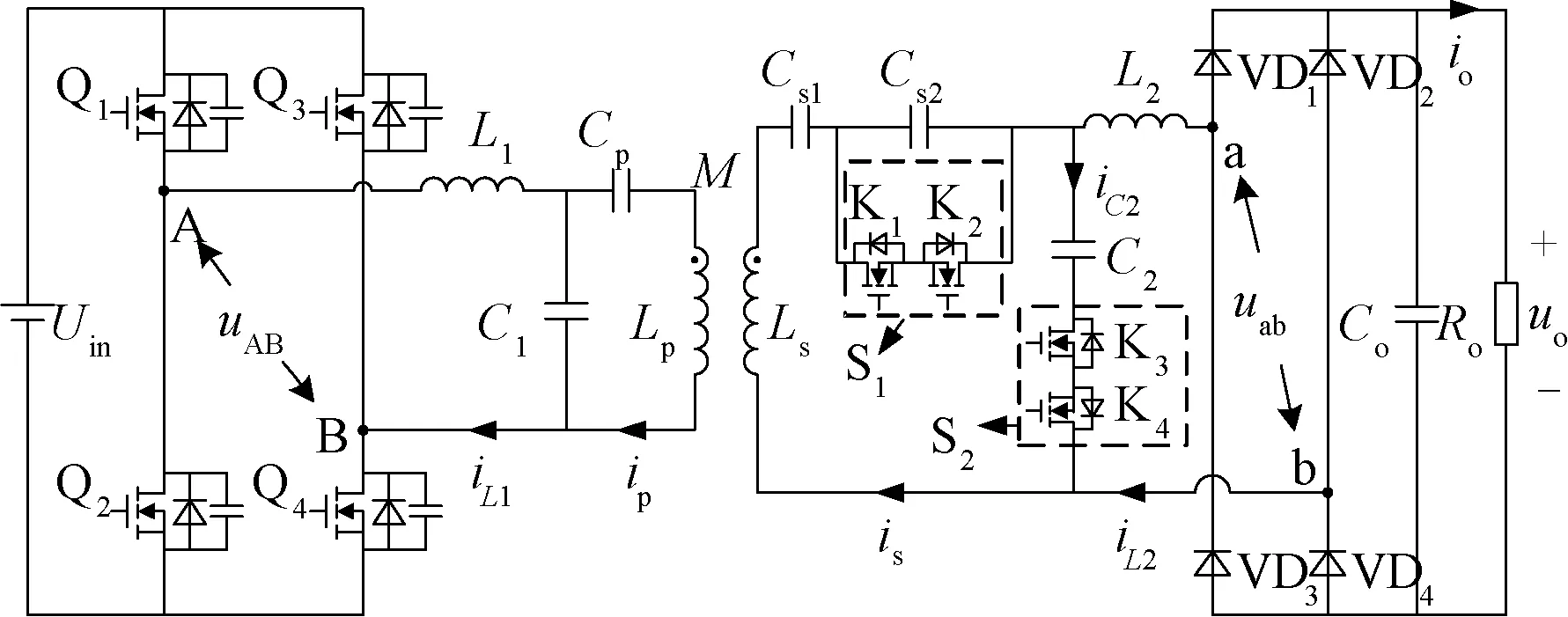
图1 LCC-LCC/S型变结构补偿WPT系统Fig.1 LCC-LCC/S configurable compensation based WPT system

在图1所示的补偿网络中，由L1、C1和Cp构成了发射端的“LCC”补偿结构。在接收端，作为模式切换控制开关，S1由MOS管K1、K2反向串联构成，S2由MOS管K3、K4反向串联构成。当S1、S2均闭合时，由L2、C2和Cs1构成“LCC”，此时的发射-接收补偿网络可等效为LCC-LCC结构。当S1、S2均断开时，L2、Cs1、Cs2形成串联(S)结构，使补偿网络变为LCC-S结构。通过控制开关S1、S2的通断，可使WPT实现恒流输出与恒压输出模式的切换。

2.1 LCC-LCC补偿网络原理分析

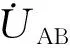
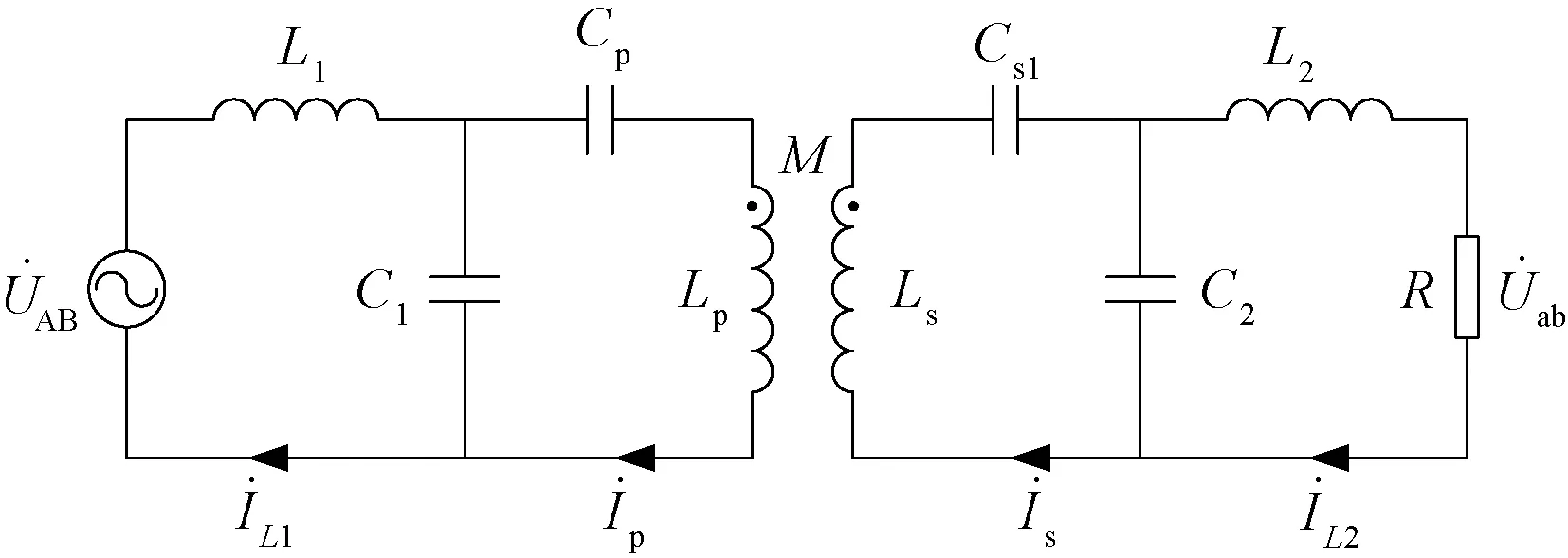
图2 LCC-LCC补偿网络等效电路Fig.2 LCC-LCC equivalent compensation network

逆变器采用180°控制方式，并将其工作频率f对应的角频率ω=2πf设定在LCC-LCC网络的固有谐振角频率ωs处，即ω=ωs，ωs为：

(1)

工作在谐振状态下的接收端输入阻抗Zs可表示为：

(2)

将接收端折算到发射端的反射阻抗用Zr表示，可得：

(3)

发射端在谐振频率点处的输入阻抗Zin可表示为：

(4)

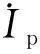
(5)

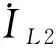
(6)

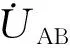
2.2 LCC-S型补偿网络原理分析

断开S1、S2构成的LCC-S补偿网络如图3所示。假设接收端补偿网络满足：[1/(jωsCs1)]+[1/(jωsCs2)]+jωsL2=1/(jωsCs)，配置Cs参数，使其满足式(7)所示：

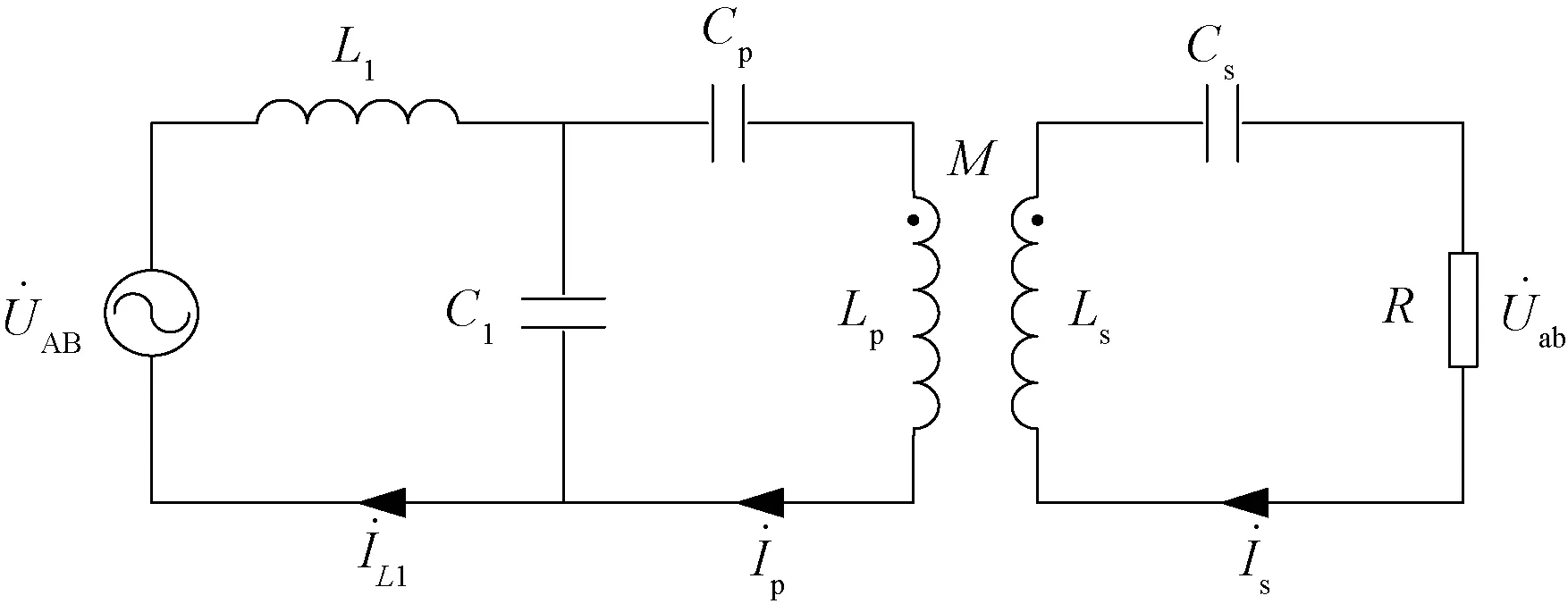
图3 LCC-S型补偿网络等效电路Fig.3 LCC-S equivalent compensation network

(7)

则接收端的输入阻抗Zs为：

(8)

将接收端折算到发射端的反射阻抗用Zr表示为：

(9)

发射端的输入阻抗Zin为：

(10)

与LCC-LCC补偿网络相同，LCC-S补偿网络输入阻抗为阻性，保持了逆变器的ZPA特性。

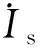
(11)

(12)

综上，LCC-LCC/S型变结构补偿网络，仅需定宽定频控制即可实现系统的恒流-恒压输出，不依赖于反馈量，避免了对无线通信的依赖。

2.3 模式切换控制策略

在WPT系统实现恒流-恒压模式切换的暂态过程中，假设构成S1的K1、K2和构成S2的K3、K4分别采用相同的控制逻辑，则直接关断S1，电流可以流过Cs2并联支路，由于该电容对电压的钳位作用，S1基本不受冲击。不同的是，若S2采用硬关断，将造成接收端电感L2上的电流突变(强行使is和iL2变为同一相位)，产生的电压应力会威胁S2工作安全。图4给出了在关断过程中，K3、K4的驱动电压uK3、uK4及接收线圈电流is、电感L2电流iL2、电容C2电流iC2的仿真波形。

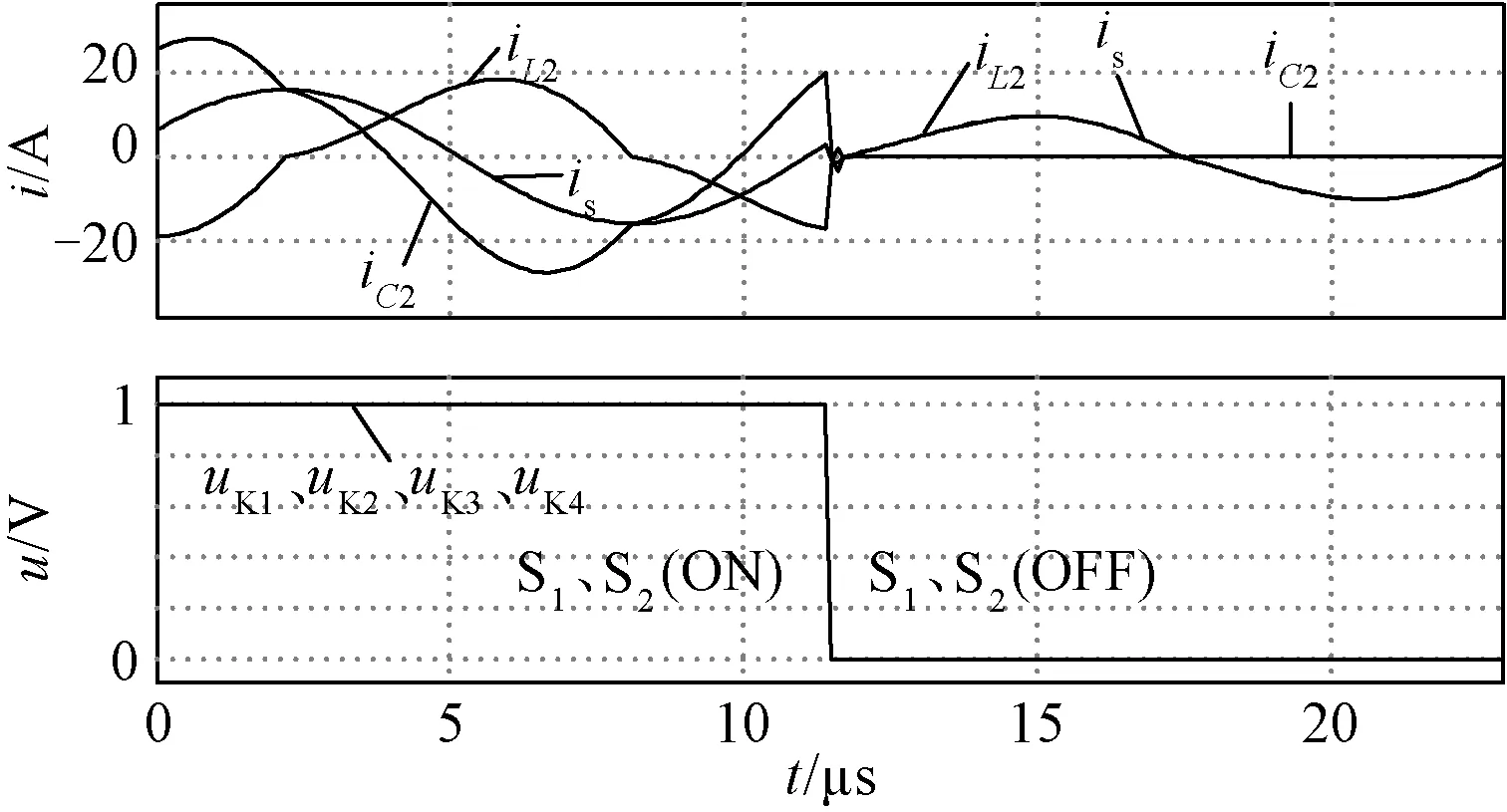
图4 S2硬关断的暂态仿真波形Fig.4 Simulated waveforms under hard switching of S2

针对S2关断问题，本文设计了一种开关切换时序优化控制策略，其仿真波形如图5所示。通过检测S2上电流流向，在谐振电流正向流经S2(iC2>0)的过程中关断K4，K4体二极管导通，使S2变成单向可控开关；再经过半个谐振周期的延迟，当S2电流谐振至反向(iC2<0)时，已被K4反向截止，此刻关断K3，则S2彻底关断，迫使C2退出网络，使is同iL2形成同一环路，即可实现模式的平滑过渡。

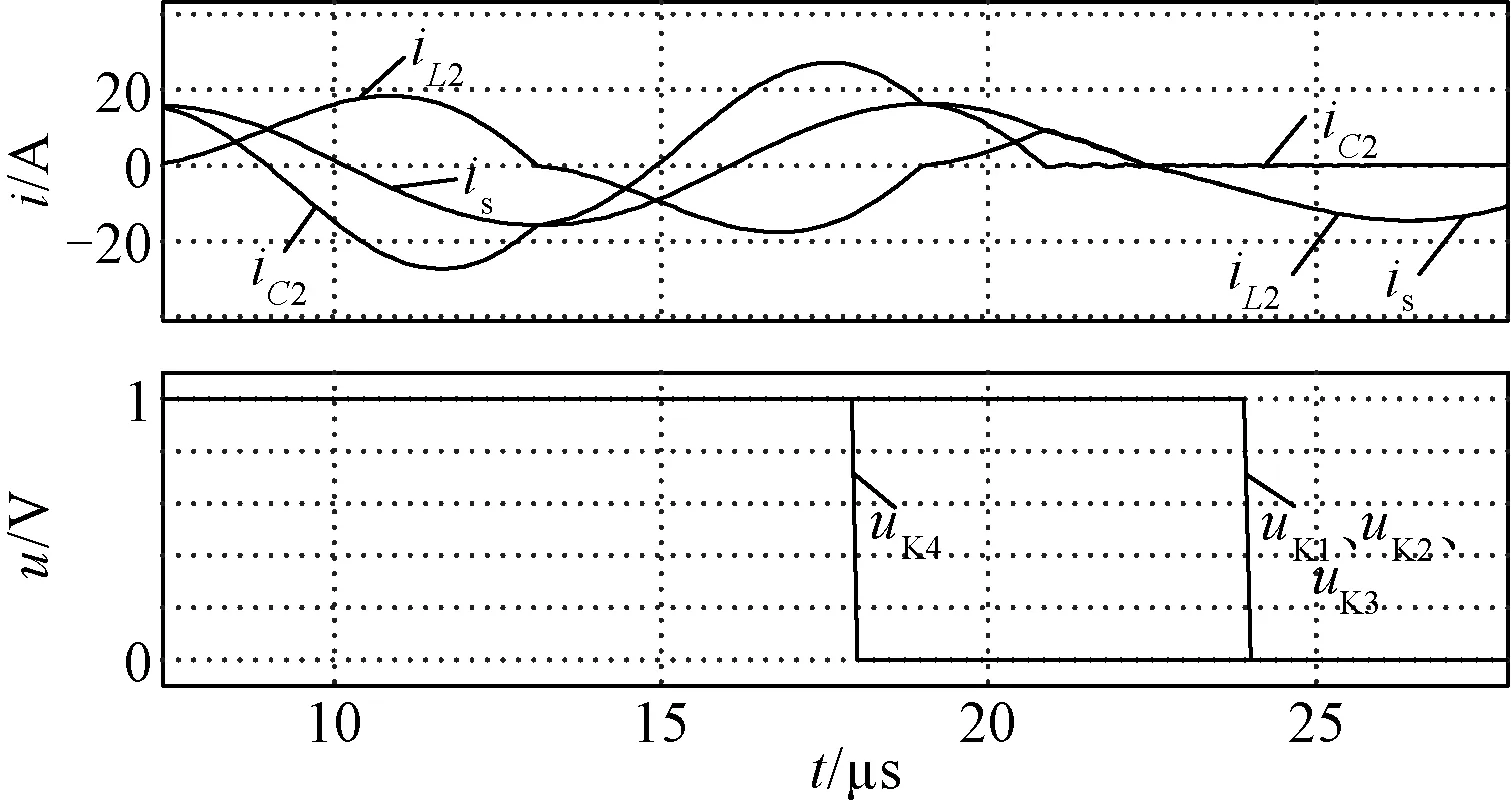
图5 时序切换仿真波形Fig.5 Simulated waveforms under proposed switching order

3 实验

为了验证控制策略的正确性，本文针对电动车辆用96 V/100 A·h大功率锂电池进行储能实验，搭建1 kW实验平台，利用功率电阻模拟蓄电池充电任务。充电过程设定为：首先起动恒流充电；在电压达到阈值105 V后，通过模式切换转为恒压充电。其恒压阶段标称电压96 V(实验中输出电压变化范围取为38～107 V)，恒流阶段快充电流容量10 A。实验过程中，逆变器始终工作在f=85 kHz的开环控制下，样机主要参数见表1。

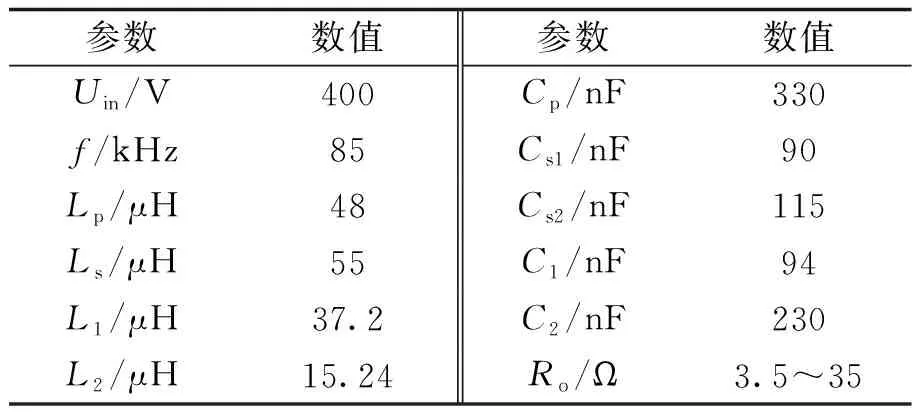
表1 主要实验参数Tab.1 Key experimental parameters

图6～图9给出了恒流充电模式下的开关Q2驱动电压ugs、漏源电压uds、补偿网络输入电流iL1、发射线圈电流ip、接收线圈电流is、接收端桥臂中点电压uab、整流桥输入电流iL2的波形。当负载Ro在3.5～10 Ω范围内变化时，充电电流在10.9～10.5 A范围内基本保持恒定。由于方波中含有基波外的谐波，逆变电流滞后uAB电压，有利于逆变器实现ZVS。

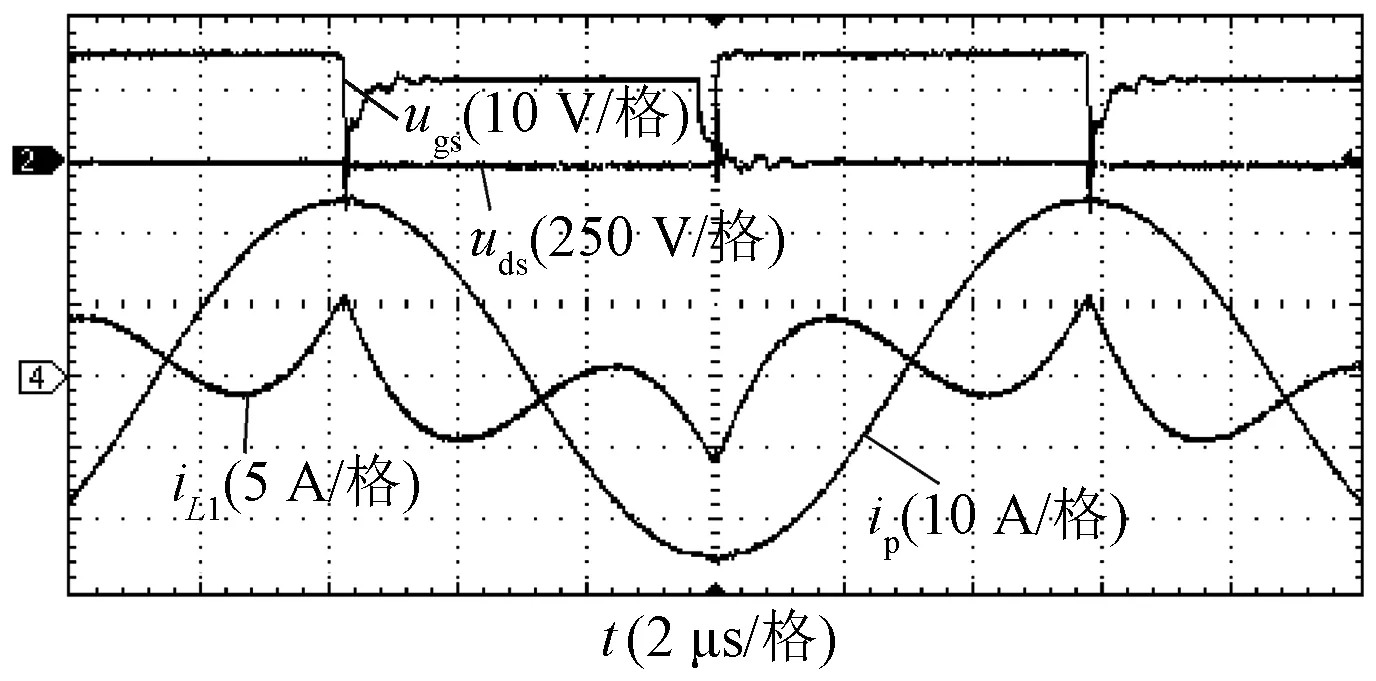
图6 恒流模式下的发射端主要实验波形(Ro=3.5 Ω)Fig.6 Key experimental waveforms of transmitter-side in constant current output mode with Ro=3.5 Ω

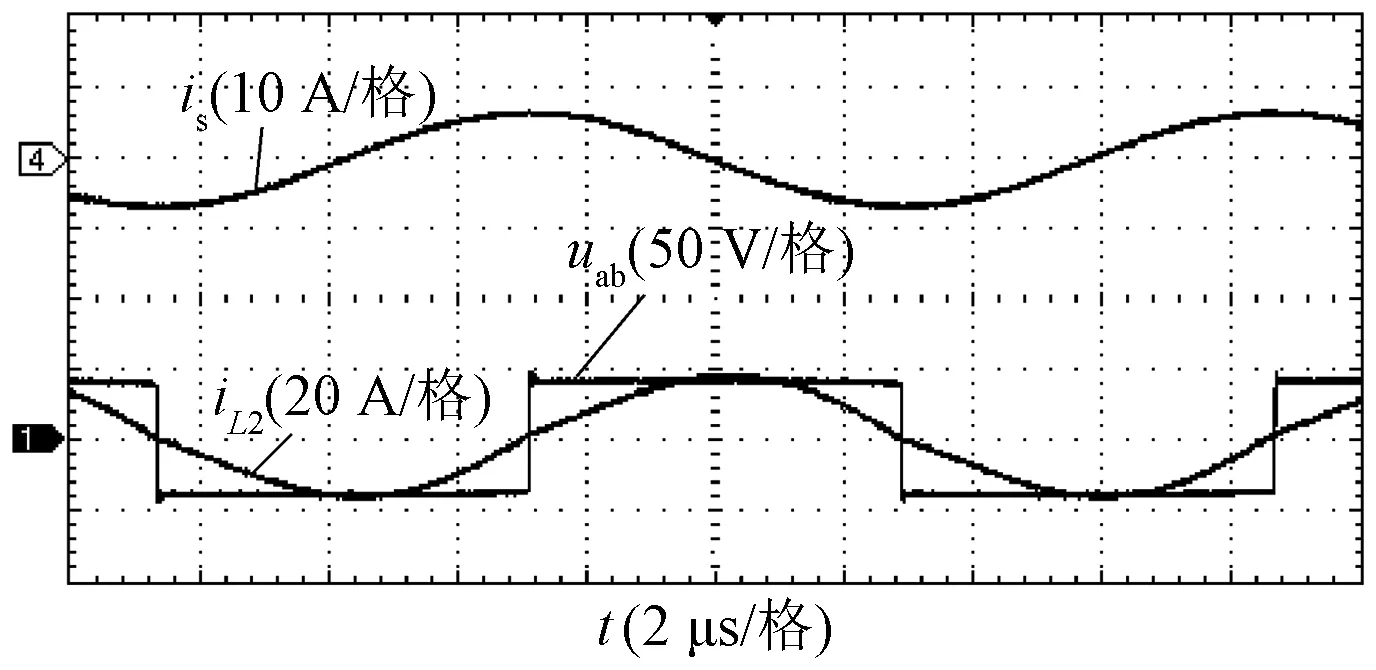
图7 恒流模式下的接收端主要实验波形(Ro=3.5 Ω)Fig.7 Key experimental waveforms of receiver-side in constant current output mode with Ro=3.5 Ω

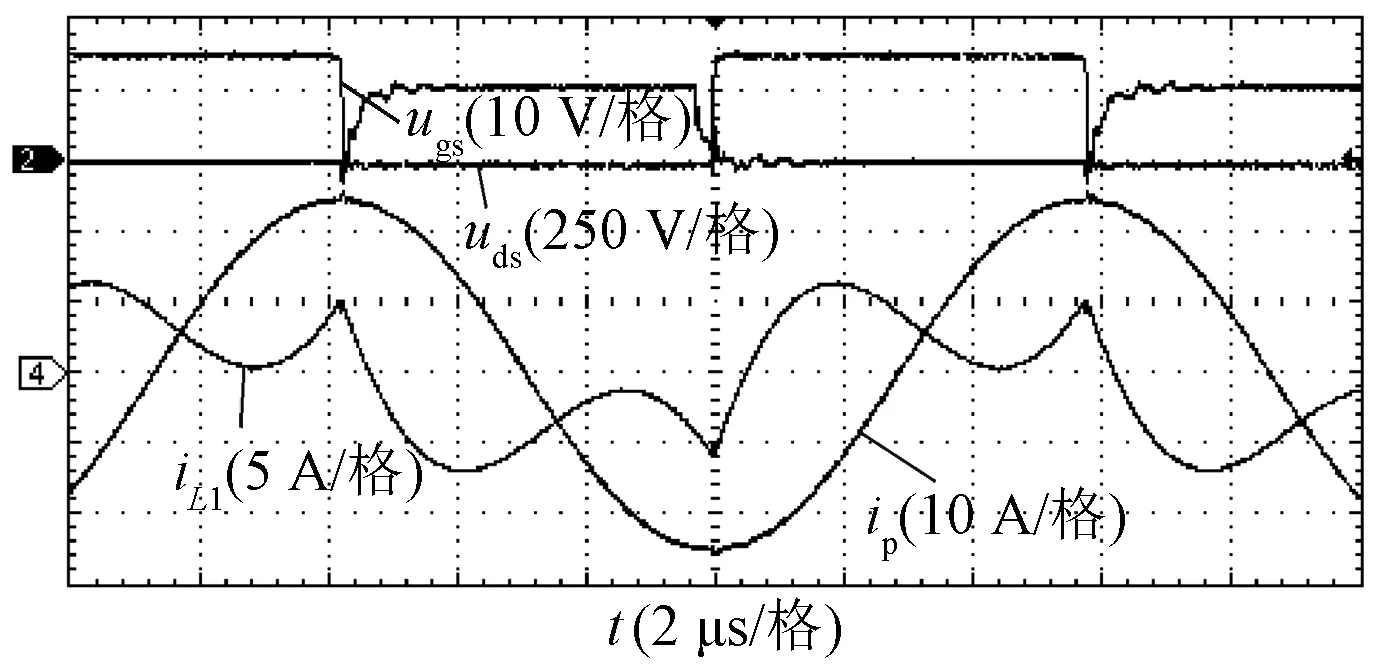
图8 恒流模式下的发射端主要实验波形(Ro=10 Ω)Fig.8 Key experimental waveforms of transmitter-side in constant current output mode with Ro=10 Ω

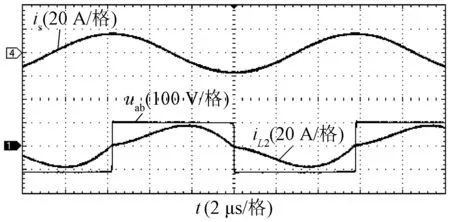
图9 恒流模式下的接收端主要实验波形(Ro=10 Ω)Fig.9 Key experimental waveforms of receiver-side in constant current output mode with Ro=10 Ω

图10和图11所示为基于LCC-S补偿的恒压模式下逆变器输出电压uAB、补偿网络输入电流iL1、整流桥中点电压uab、接收线圈电流is的波形。图10中负载Ro=10 Ω，输出电压为104.3 V；图11中负载电阻Ro=34.2 Ω，输出电压增大到107.2 V，基本可认定在该阶段内的电压在负载扰动作用下能够保持恒定。同样地，逆变器实现了ZVS。

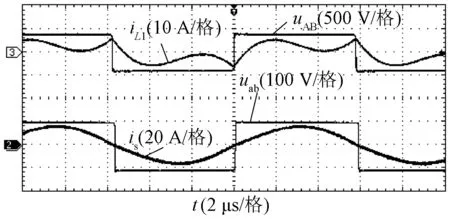
图10 恒压模式下的主要实验波形(Ro=10 Ω)Fig.10 Key experimental waveforms in constant voltage output mode with Ro=10 Ω

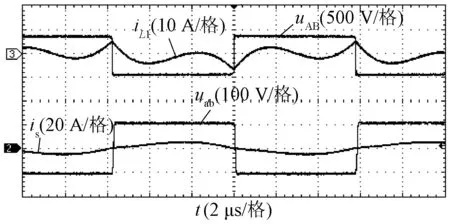
图11 恒压模式下的主要实验波形(Ro=34.2 Ω)Fig.11 Key experimental waveforms in constant voltage output mode with Ro=34.2 Ω

图12、图13和图14所示为负载阻抗Ro=10 Ω时，系统从恒流切换到恒压阶段过程中，双向开关的驱动电压uK3与uK4、S2导通电流iC2、发射线圈电流ip、接收线圈电流is、输出电压uo、输出电流io的波形。由图14可见，切换过程中，开关动作所引起的电池电压振荡较小，验证了本文提出开关时序控制策略的可行性，表明WPT系统可以从恒流模式平滑切换到恒压模式。

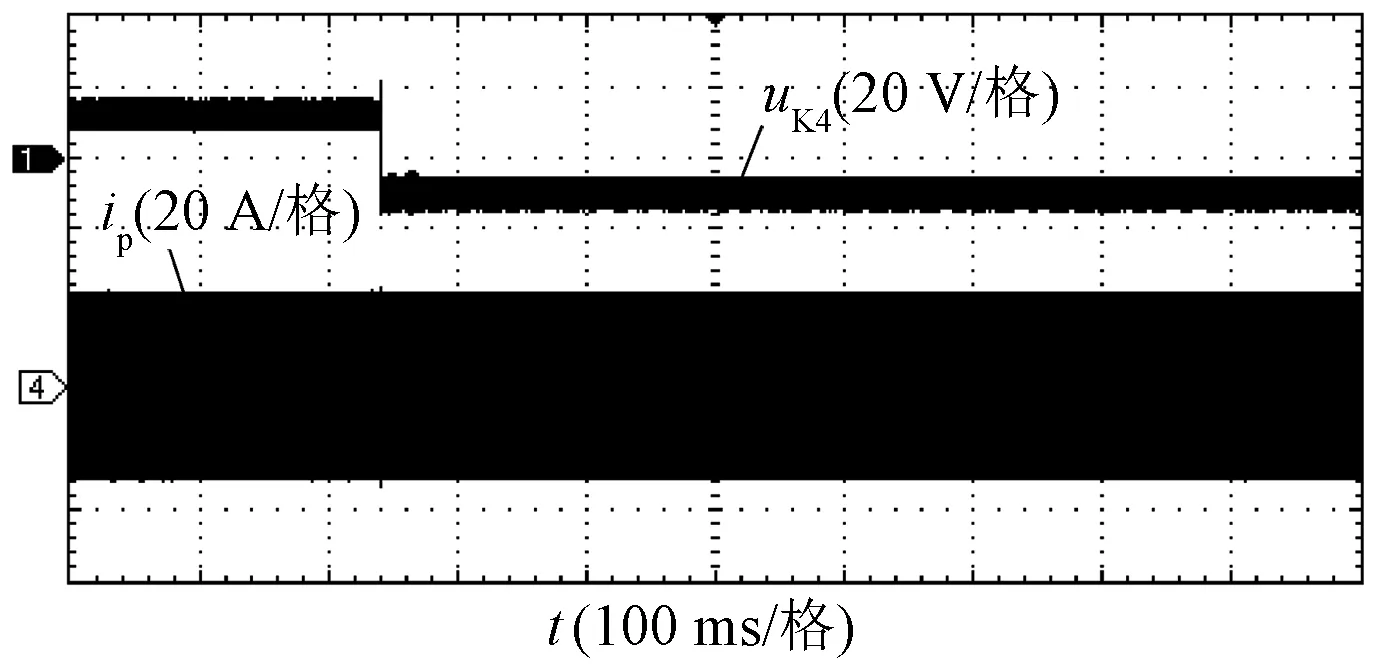
图12 模式切换暂态过程中ip和uK4波形Fig.12 Experimental waveforms of ip and uK4 during mode switching transient process

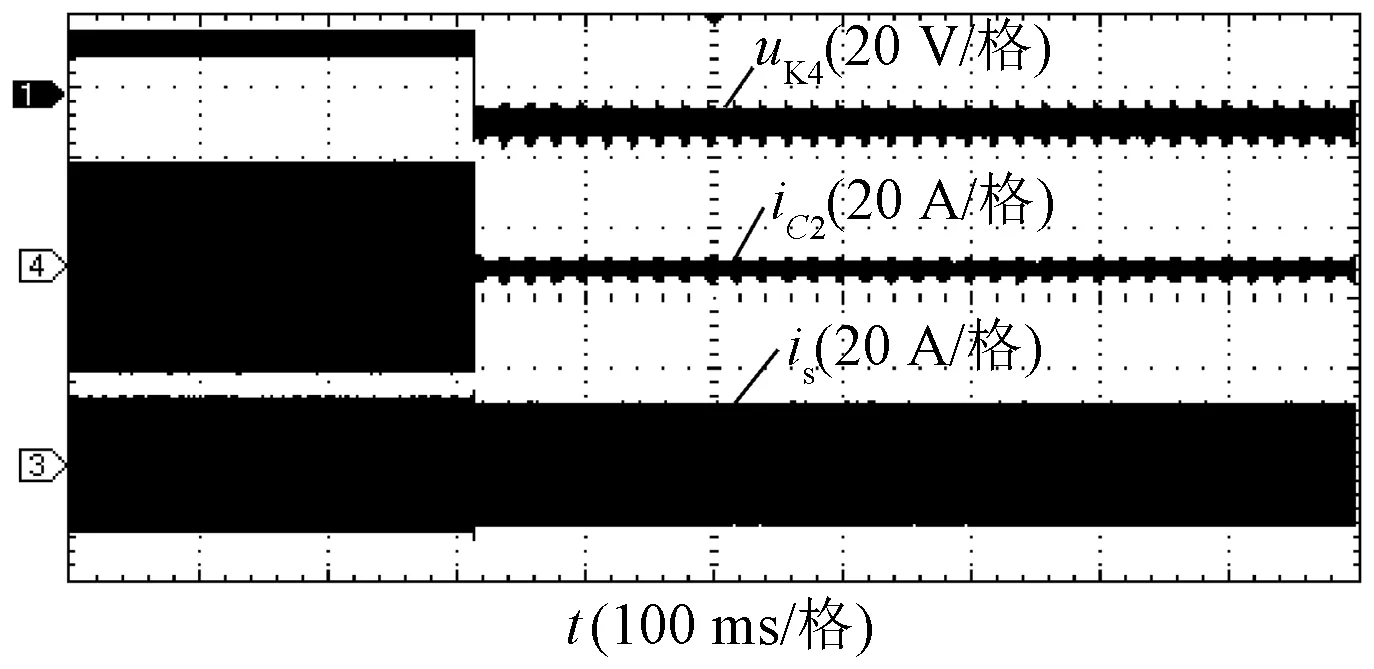
图13 模式切换暂态过程中is、iC2和uK4波形Fig.13 Experimental waveforms of is, iC2 and uK4 during mode switching transient process

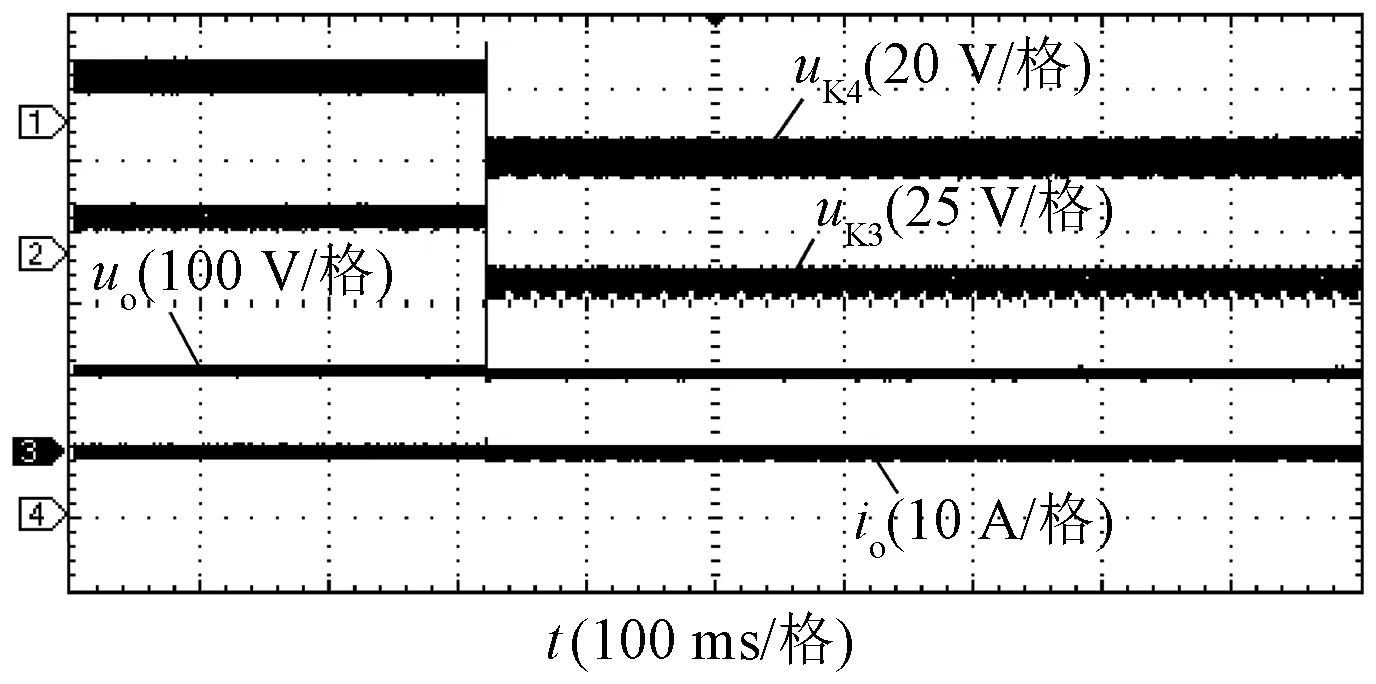
图14 模式切换暂态过程中的uo、io、uK3和uK4波形Fig.14 Experimental waveforms of uo, io, uK3 and uK4 during mode switching transient process

图15为开环控制条件下，变化Ro对系统输出电流、电压的影响曲线。考虑到有源器件管压降和线圈涡流损耗的变化，实验中输出电压、电流与理论设定存在一定偏差。恒流阶段，随着充电电压的升高，输出功率逐渐增大，并最终在到达uo的阈值105 V时提供额定1.1 kW，测得的稳态电流波动率小于3.7%；进入恒压阶段，负载从最大功率1 086 W降至336 W，相应的稳态电压变化率小于2.7%。

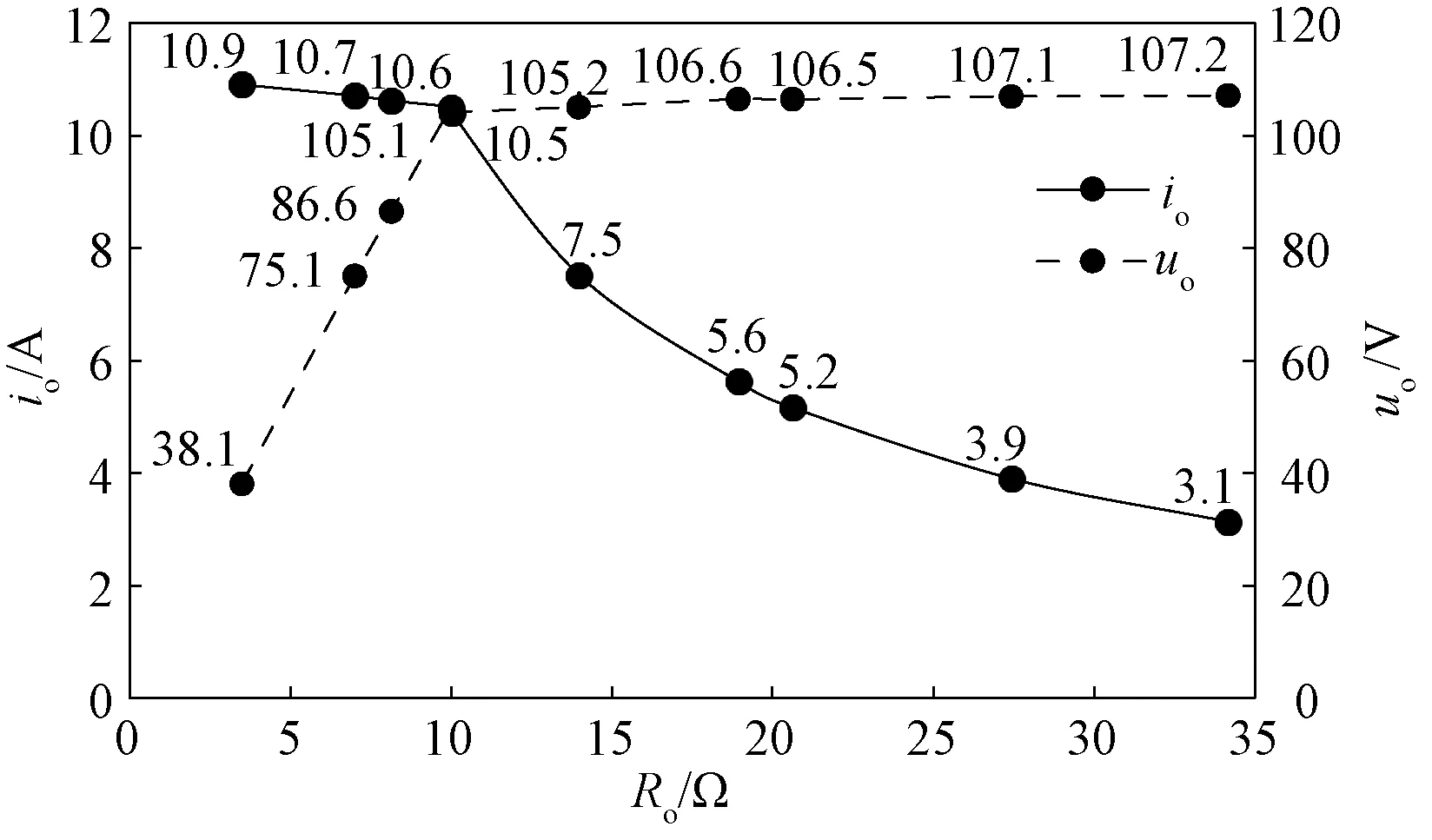
图15 负载变化对输出电流和输出电压的影响Fig.15 System output current and voltage curve under different loads

图16为负载扰动对系统效率的影响曲线。恒流阶段下系统最高效率η为87%；在恒压阶段，随着Ro的增加，输出功率逐渐降低。因此，在额定1.1 kW条件下，输出电压为105 V时，对应有系统效率最高值89.6%。考虑到恒压阶段的双向开关S1、S2均处于关断状态，无导通损耗，因此该阶段的效率相比恒流阶段有所提高。

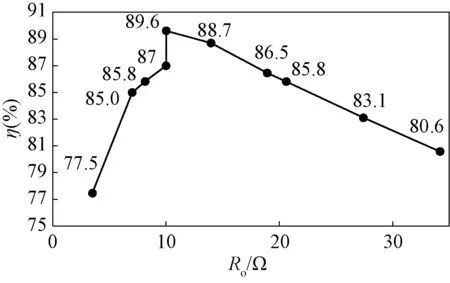
图16 不同负载下系统效率曲线Fig.16 System efficiency curve under different loads

4 结论

本文针对电动车辆动力电池充电用WPT系统的一种LCC-LCC/S型变结构补偿网络及其模式切换策略进行了分析与设计，通过优化开关切换时序，避免了能量冲击对器件工作可靠性的影响。建立了一台功率等级为1 kW的实验样机，通过实验验证可得：在负载大范围变化的恒流充电阶段，系统输出电流波动仅为3.67%，最高传输效率为87%；在恒压充电阶段，输出电压波动仅为2.7%，最高能量传输效率为89.6%。整个过程中电阻的变化范围为3.5～35 Ω，利用开环控制基本实现了恒流-恒压输出，与理论分析相吻合。此外，在双向开关切换过程中，系统的暂态振荡小，无明显冲击。本系统只考虑了恒流到恒压模式的切换，后续工作还将研究恒流、恒压两种模式的自由切换。