高频工况下高温超导带材传输损耗特性研究

张玉峰， 苏 涛， 郭 倩， 何劲飞， 周奇勋

(西安科技大学电气与控制工程学院， 陕西 西安 710054)

1 引言

随着高速旋转电机不断向更高功率密度、更小体积发展，电机绕组的载流能力与电机高速运行下的散热问题成为制约其发展的重要因素，而高温超导(High Temperature Superconducting，HTS)带材因其出色的载流能力以及极小的热损耗为高速旋转电机的发展提供了新的可能，HTS带材在交变电流和交变磁场环境下的损耗特性研究也成为超导电机研究领域内的热点问题[1-5]。HTS带材的交流损耗根据其所添加电流、磁场条件可分为磁化损耗和传输损耗。其中，本文重点研究的传输损耗定义为：HTS带材在无外部磁场的条件下仅传输交变电流时所产生的交流损耗称为传输损耗[6-8]。目前，在高速电机相关研究中，各类高速电机频率已达到104Hz及以上[9]，而超导电机作为研究热点，目前电机频率已经达到kHz以上并具有继续提高的趋势[10]。并且，在kHz交变电流范围内，已有针对HTS带材传输损耗特性展开的研究[11,12]。而在目前高速电机向更高功率、更高频率发展的趋势下，应用于超导电机的HTS带材在MHz频率下的传输损耗对电流频率及幅值的依赖性还有待明确。因此，对于MHz频率下HTS带材的传输损耗特性展开相关研究，在高速电机领域极为必要。

本文建立了基于H公式的HTS带材多层结构的仿真模型，进行了1 MHz电流频率范围内传输损耗的数值仿真。考虑到临界电流是超导体重要的边界参数之一，仿真中以其作为参变量研究超导带材在工程应用时可能的最大损耗变化规律。基于仿真结果，研究了传输损耗对电流幅值及频率的依赖性，得出了MHz频率内电流频率及幅值变化对多层HTS带材传输损耗的影响情况和损耗变化规律。研究结论可为MHz频率下的高速超导电机研究提供参考，同时为相关领域中高频交变电流工况下的HTS带材损耗特性研究提供借鉴。

2 基于H公式的HTS模型

本文以上海超导生产的第二代HTS带材为对象，进行了多层结构的建模。所建多层结构二维截面图如图1所示。所建模型包括了铜稳定层、银保护层、柔性基底层和超导层，各层位置分布以及厚度比例已在图1中标注。

图1 HTS带材多层结构截面图Fig.1 Section diagram of multilayer structure of HTS tape

图2为三维视角下HTS带材多层结构分布图，如图2中标注所示，传输损耗仿真所需交变电流从垂直于多层带材横截面的方向进行添加。

图2 三维下HTS带材结构分布图Fig.2 Structure distribution of HTS tape in 3D

为了说明HTS多层模型的传输损耗变化情况，建立了与多层模型具有相同横截面积，分别由铜带材填充的铜薄膜模型和仅有超导材料填充的超导薄膜模型，用来进行传输损耗的对比分析。以上两种模型二维截面图如图3所示。

图3 铜薄膜模型和超导薄膜模型截面图Fig.3 Cross sections of copper film model and HTS film model

在所建多层结构HTS带材和其他模型基础上，借助有限元仿真软件Comsol，本文建立了基于H公式的HTS带材电磁仿真模型[13,14]。

2.1 基于H公式的控制方程

仿真中基于H公式的控制方程由麦克斯韦方程推导得出，首先，根据法拉第定律有：

(1)

B=Bself+Bext

(2)

式中，E为电场强度；B为总磁通密度；Bself为自场磁通密度；Bext为外场磁通密度。

由式(1)可得：

(3)

H=Hs+Hext

(4)

式中，H为总磁场强度；Hs为自场磁场强度；Hext为外场磁场强度；μ为磁导率。

根据安培定律和欧姆定律有：

▽×H=J

(5)

E=ρJ

(6)

式中，J为电流密度；ρ为HTS带材电阻率。

将式(5)、式(6)代入式(3)即可得到基于H公式的方程的一般形式：

(7)

式中，μ0为真空磁导率；μr为材料相对磁导率。

对于超导层而言，有E-J幂次定律：

(8)

即超导层电阻率：

(9)

式中，Ec为HTS临界电场标准，Ec=10-4V/m；n为E-J幂次定律拟合指数；Jc为HTS临界电流密度。

2.2 多层结构传输电流条件

HTS带材各层传输电流约束方程：

(10)

Im=pIc0

(11)

式中，Im为HTS带材传输电流幅值；Ic0为HTS带材最大临界电流；S为多层结构中每一层的横截面积；p为归一化电流比值，p=Im/Ic0；f为交变电流频率。

为了计算HTS带材每一层单位时间内的传输损耗，有：

(12)

式中，Q为HTS带材单位时间内的传输损耗。

因此，HTS带材单位时间内各层总传输损耗为：

QTot=QCu+QAg+QHTS+QSub

(13)

式中，QTot为总交流损耗，即总传输损耗；QCu为铜稳定层传输损耗；QAg为银保护层传输损耗；QHTS为超导层传输损耗；QSub为柔性基底层传输损耗。

2.3 基于Comsol的系统控制方程

通常在基于H方法的三维电磁场问题中，H方法的待求解变量为磁场强度H=(Hx,Hy,Hz),其对应的电场强度E=(Ex,Ey,Ez)，电流密度J=(Jx,Jy,Jz)。当仅考虑二维电磁场进行仿真建模时，磁场强度H的z方向分量为0，电场强度E的x，y方向分量为0，即在二维情况下磁场强度H=[Hx(x,y),Hy(x,y),0]，电场强度E=[0,0,E(x,y)]。将二维情况下的磁场强度向量和电场强度向量代入式(3)、式(5)中，可得二维情况下H方法中电流密度表达式以及电场强度表达式：

(14)

(15)

将式(14)、式(15)代入基于H方法的系统控制方程式(7)可得其在二维情况下完整形式：

(16)

得出基于H方法的控制方程后，本文利用Comsol有限元仿真软件中的PDE偏微分方程模块，实现将基于H方法的控制方程转换为Comsol有限元仿真软件中的控制方程形式。软件中给出了PDE模块偏微分方程的标准形式为：

(17)

(18)

式中，u为非独立变量的矢量形式；ea为质量系数矩阵；da为阻尼系数；F为源项；Γ为通量向量。

将基于H方法二维控制方程式(16)代入式(17)可得出Comsol下PDE模块系统控制方程为：

(19)

2.4 基于Comsol的多层结构二维仿真模型

在Comsol的二维瞬态模型下建立的基于H公式的HTS带材多层结构仿真模型如图4所示。模型采用圆形求解域模拟超导带材所处无限大空气域，并采用自由三角形网格对空气域进行剖分。

图4 HTS带材二维仿真模型Fig.4 2D simulation model of HTS tape

图5为HTS带材多层结构局部放大图，超导层采用宽厚比为100∶1的矩形，各层的位置分布以及厚度比例如图4中标注所示，每层的宽度以及厚度均已剖分为固定数量的线段。带材传输电流以逐点约束的形式添加。

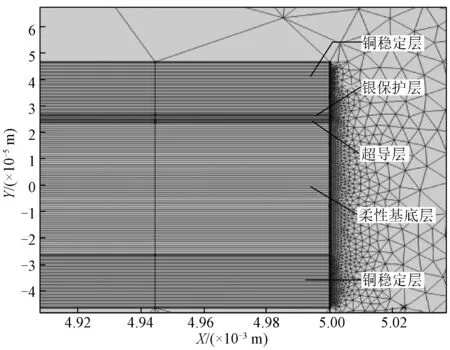
图5 HTS带材多层仿真模型局部图Fig.5 Local diagram of multilayer simulation model of HTS tape

表1为HTS带材多层结构中各层电阻率、厚度等相关参数。

表1 HTS带材有限元仿真参数Tab.1 Finite element simulation parameters for HTS tapes

3 传输损耗特性仿真及分析

3.1 传输损耗对交变电流频率的依赖性

图6为传输损耗与交变电流频率的相关性曲线。图6(a)和图6(b)分别为交变电流幅值0.5Ic0和Ic0。这里采用Brandt方程(式(20))进行了传输损耗的解析计算，并对超导薄膜模型、铜薄膜模型和超导多层模型进行了仿真计算，具体公式如下：

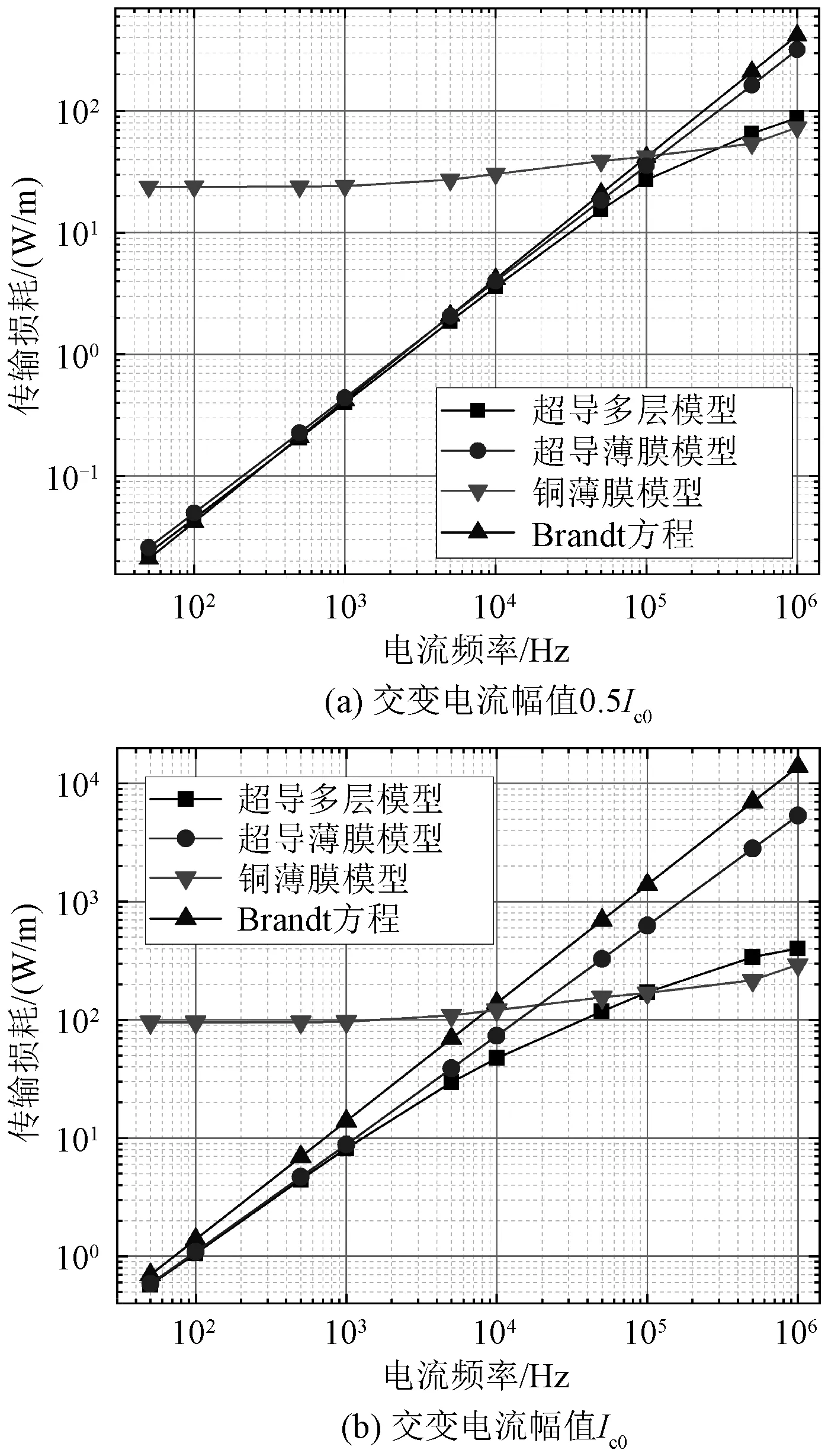
图6 传输损耗频率依赖性曲线图Fig.6 Frequency-dependent curve of AC transport current loss

(20)

式中，Qtrans为传输损耗。

由图6可知，四种模型损耗计算结果均与电流频率呈正相关。传输损耗受电流频率和幅值的共同影响，为了更好地描述传输损耗在不同频率内的变化情况，综合考虑HTS带材中趋肤效应的影响和传输损耗的变化趋势，定义频率低于104Hz为中低频区域，频率高于105Hz为高频区域，而104～105Hz区域为不同电流条件下传输损耗变化的过渡区域。其中，基于H公式的超导薄膜模型与Brandt方程的计算结果表现出高度的一致性。铜薄膜模型仿真结果显示铜薄膜模型传输损耗在中低频段远高于其他模型损耗，而在高频段低于其他超导模型损耗。而基于H公式的超导多层模型，虽然在中低频段中损耗曲线和其他超导模型保持一致，但当电流频率增加到104Hz以上时，其损耗增加速率不断减小，损耗曲线不断逼近铜薄膜模型。并且超导多层模型损耗结果与超导薄膜模型和Brandt计算模型损耗结果具有较大差别。

由上述分析可知，当电流频率处在中低频段时，铜稳定层等金属层对超导多层模型的传输损耗不造成显著影响，但当电流频率处在104Hz以上的高频段时，铜稳定层等金属层的传输损耗贡献不可被忽略，并且说明在高频段内，Brandt方程不再适用于超导多层模型的传输损耗计算。

除此之外，同频率下高幅值电流体现出更高的传输损耗，并且，传输电流为0.5Ic0时，损耗曲线斜率从频率105Hz处开始减小，而传输电流为Ic0时，曲线斜率则从频率104Hz处开始减小，说明传输损耗的频率依赖性一定程度受到电流幅值的影响，并且传输电流幅值越高，影响越显著。

图7为超导多层模型各层传输损耗频率依赖性曲线。

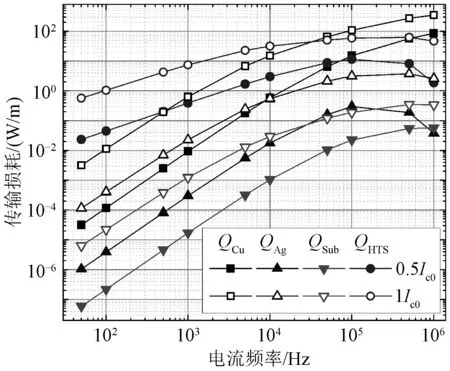
图7 各层传输损耗频率依赖性曲线图Fig.7 Frequency-dependent curve of AC transport current loss for each layer

由图7可得，多层带材各层损耗在中低频段时均与电流频率呈正相关，其中铜稳定层的损耗增长速率最快。但当频率增加到105Hz以上时，除铜稳定层外各层传输损耗均呈现不断减小的趋势，并且随着频率的增加，减小速率不断增加。

图8为超导多层模型各层传输损耗占比分布图。由图8可知，随着电流频率增加，铜稳定层损耗占比由0.13%增加到97.77%，逐渐占据传输损耗主导地位，超导层损耗占比则由99.86%不断减小到2.12%，其余各层损耗贡献极小并基本保持稳定。

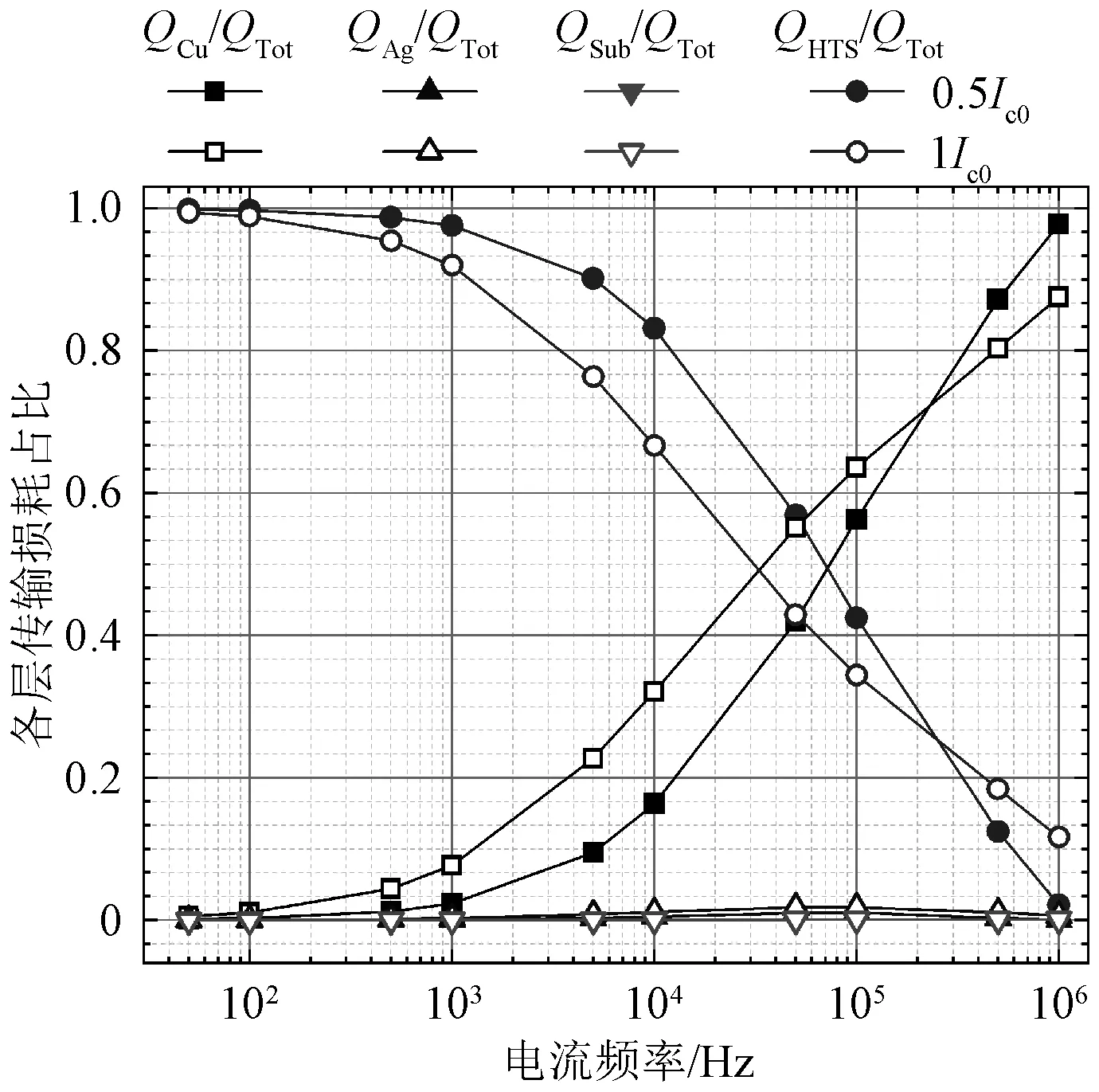
图8 各层传输损耗占比分布图Fig.8 AC transport current loss ratio of each layer

为进一步研究图7、图8中各层传输损耗及损耗占比的变化规律，图9给出多层结构HTS模型电流密度随电流频率变化的数值对比图。由图9可知，在电流频率从50 Hz增加到1 MHz过程中，超导层电流密度与频率变化呈负相关，其余各层均与频率呈正相关。其中最靠近带材表面的铜层电流密度增幅最大，由1.55×106A/m2增加到5.04×108A/m2。而超导层电流密度则由2.94×1010A/m2下降到9.59×109A/m2。在整个频率变化过程中，铜层电流密度由总电流密度的0.005 3%增长到4.95%，而超导层电流密度则由99.99%下降至94.20%。

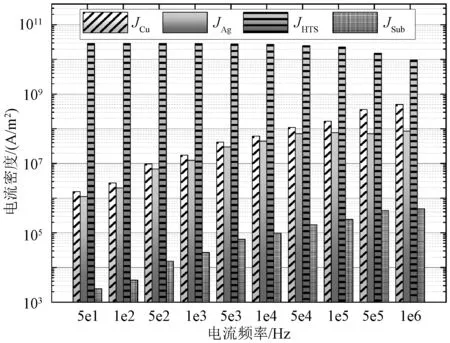
图9 各层电流密度数值对比图Fig.9 Comparison diagram of current density values of each layer

图8和图9的数据变化说明，随着频率变化，各层电流分布发生明显变化，铜稳定层涡流电流显著增加，铜稳定层的涡流损耗也明显增加，而超导层电流明显减小，超导层损耗也随频率增加而降低。

综上分析，在中低频段中，超导层损耗为传输损耗主要来源但其损耗贡献随频率增加不断减小。而在高频段中，铜稳定层损耗显著增加，其损耗贡献逐渐取代超导层在传输损耗中占据主导地位。以上结果反映出多层结构超导带材的传输损耗具有较强的电流频率依赖性，结合图9中各层电流密度的数值变化，说明频率变化引起的各层电流分布变化是造成传输损耗变化规律发生改变的主要原因。

3.2 传输损耗的交变电流幅值依赖性

图10为传输损耗电流幅值依赖性曲线图，图10(a)和图10(b)分别为交变电流频率50 Hz和1 MHz。这里同样采用Brandt方程进行了传输损耗的解析计算，并对超导薄膜模型、铜薄膜模型和超导多层模型进行了仿真计算。

图10 传输损耗幅值依赖性曲线图Fig.10 Amplitude-dependent curve of AC transport current loss

由图10数据变化规律可知，四种模型损耗计算结果均与电流幅值呈正相关。其中，基于H公式的超导薄膜模型与Brandt方程的计算结果表现出高度的一致性。而铜薄膜模型传输损耗在工频环境中远高于其他模型损耗，在高频下与超导薄膜模型损耗差异不断增大。而基于H公式的超导多层模型，在工频下损耗曲线与超导薄膜模型损耗曲线高度吻合，但在高频下随着电流幅值增加其损耗不断逼近铜薄膜模型并保持较高的一致性，同时与超导薄膜模型及Brandt公式的传输损耗计算结果差异不断增大。

由图10数据分析可知，超导多层模型传输损耗对电流幅值的依赖性取决于电流频率，电流幅值的增长，并不能对传输损耗中不同层的损耗贡献产生决定性影响。

图11为超导多层模型各层传输损耗幅值依赖性曲线。由图11可得，多层带材各层损耗均与电流幅值呈正相关，传输损耗整体表现为各层高频下损耗均高于工频。

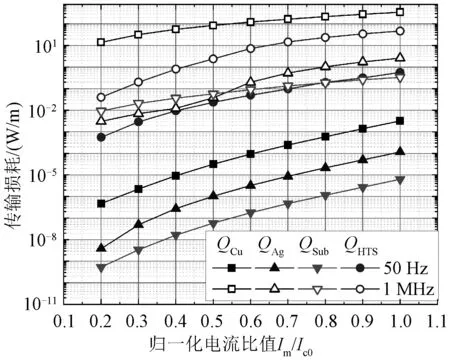
图11 各层传输损耗幅值依赖性曲线图Fig.11 Amplitude-dependent curve of AC transport current loss for each layer

图12为超导多层模型各层传输损耗占比分布图。由图12可得，工频下超导层损耗始终占据主导地位，而高频下传输损耗主要来源于铜稳定层，并且随着电流幅值增加铜稳定层损耗占比明显减小，超导层损耗占比明显增加。说明电流频率越高，电流幅值变化对传输损耗的影响越大。

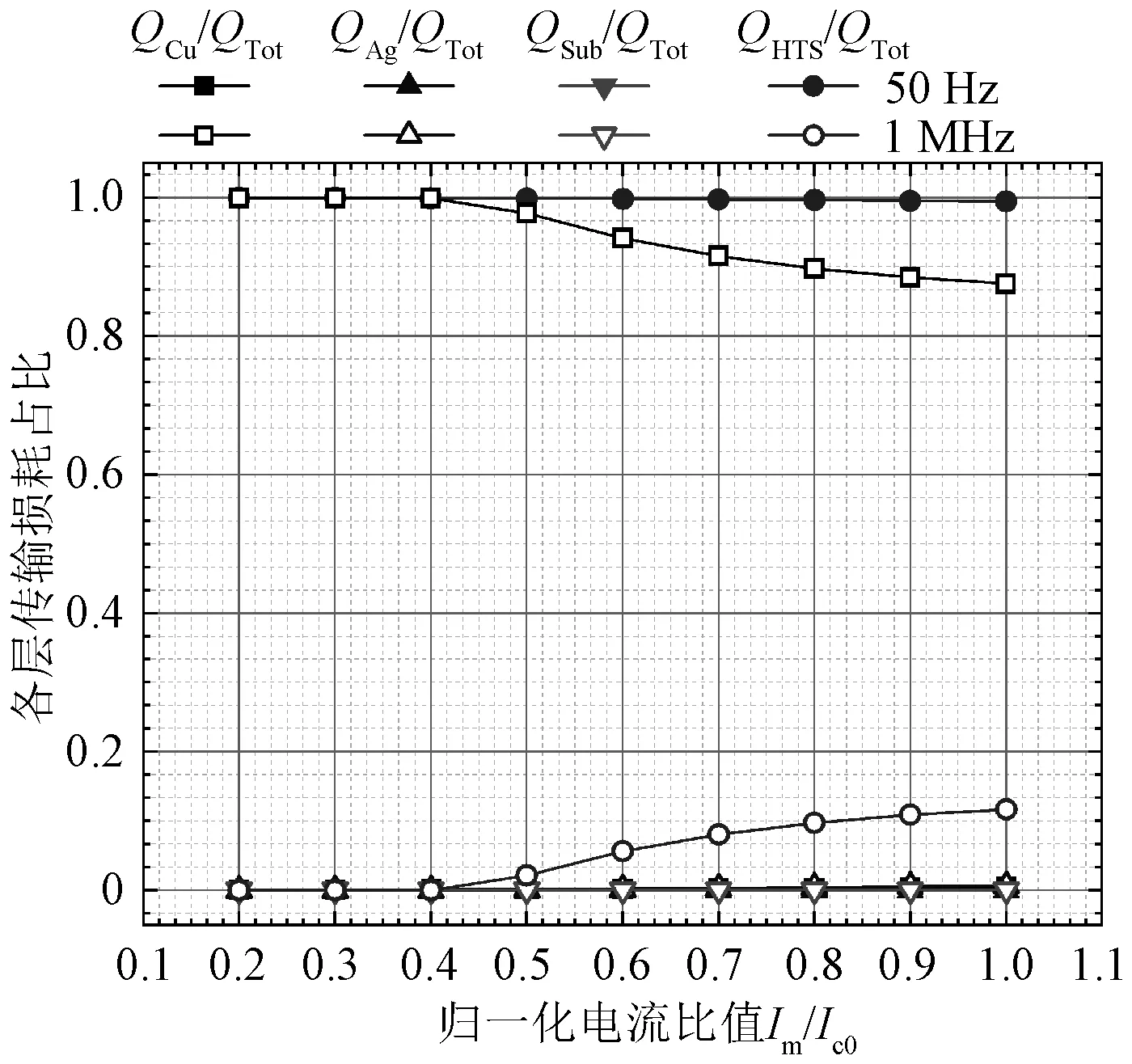
图12 各层传输损耗占比分布图Fig.12 AC transport current loss ratio of each layer

为了进一步研究图11、图12中各层传输损耗及传输损耗占比的变化规律，图13给出了HTS多层模型电流密度随电流幅值变化的数值对比图。由图13数据变化规律可知，随着电流幅值的增加，HTS多层模型中各层的电流密度均有不同程度的增长。其中铜层的电流密度由4.63×107A/m2增加到了4.92×108A/m2，电流密度占比由3.89%增加到4.59%。相比于前面得到的电流密度随频率变化的规律，幅值变化导致的各层电流密度的增长幅度均较小，并且多层结构超导带材中各层的电流分布没有产生明显变化。

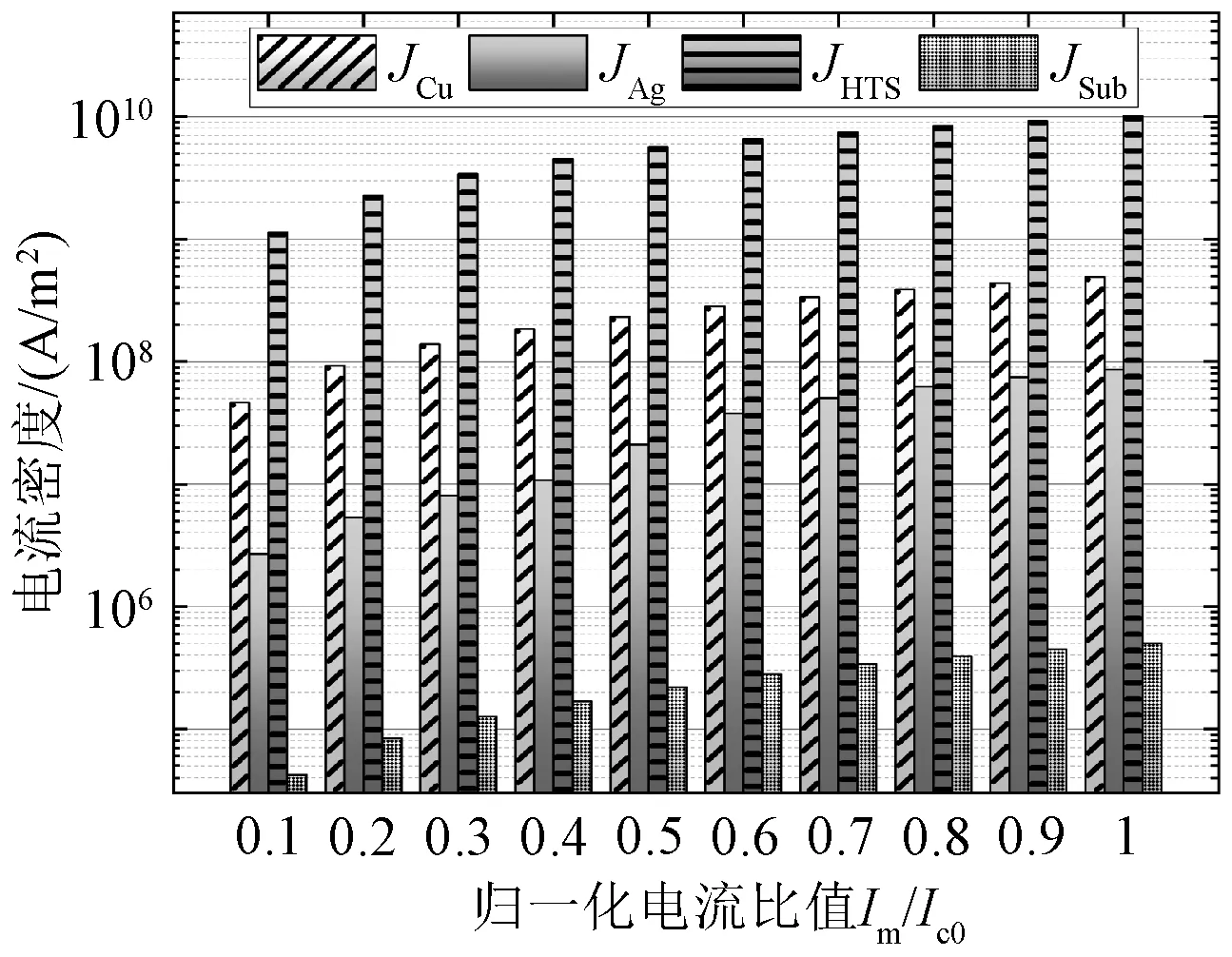
图13 各层电流密度数值对比图Fig.13 Comparison diagram of current density values of each layer

图12和图13的数据变化说明，传输电流幅值的改变并没有改变超导带材各层电流的分布情况，虽然传输交变电流幅值的变化也导致了传输损耗发生数值变化，但并没有对传输损耗的变化规律产生决定性影响。

综上分析，传输损耗对电流幅值的依赖性较小，传输损耗的变化规律仍主要取决于传输损耗的电流频率特性。

4 结论

本文考虑了HTS带材的实际多层结构，借助Comsol软件建立了基于H公式的HTS带材多层结构二维仿真模型，在50 Hz到1 MHz的频率范围内对不同幅值、不同频率交变电流的传输损耗进行了数值仿真，研究了传输损耗对电流频率及幅值的依赖性，并对HTS带材的损耗变化规律进行了讨论。仿真结果表明：

(1)HTS带材传输损耗对电流频率的依赖性大。在中低频段中，超导层损耗为传输损耗主要来源但其损耗贡献随频率增加不断减小；而在高频段中，铜稳定层损耗显著增加逐渐取代超导层在传输损耗中占据主导地位。并且，随着铜稳定层损耗贡献的增加，Brandt计算模型不再适用于高频下HTS多层带材传输损耗的计算。

(2)传输损耗对电流幅值的依赖性小。研究表明电流幅值的变化并不能对传输损耗变化规律产生决定性影响，幅值变化仅对传输损耗数值大小产生影响，传输损耗的变化规律往往取决于传输损耗的电流频率特性。

综上所述，本文通过研究多层结构HTS带材在MHz频率内传输损耗对电流频率及幅值的依赖性，说明了在实际商用多层带材结构中，铜稳定层等金属层的传输损耗贡献不可被忽略。研究结果可为HTS带材在MHz频率内传输损耗特性的研究提供参考。