探寻命题方向 奠基高考备考

刘大伟, 李勇霞

(江津中学校，重庆 402260)

通过对2021年新高考和全国卷的试题剖析，不难发现试题更加注重对高中数学基础知识、基本技能、基本方法及基本数学思想的考查，同时，具备起点低、跨度大、层次多、角度广的特点[1].因此，在高考复习过程中，不仅要夯实基础，更要注重回顾教材，加强对数学本质的理解，拓展知识网络，拓宽知识广度，促进学生数学核心素养能力的提升.

1 试题特点剖析，了解命题动向

2021年新高考数学命题始终坚持思想性与科学性的高度统一，坚持以核心素养为导向，发挥数学应用广泛、联系实际的学科特点，突出立德树人导向，重点考查学生运用所学知识分析问题和解决问题的能力，创新试题形式，注重联系社会生活实际，呈现具有教育意义的试题，提高了学生的社会责任感，引导学生形成正确的世界观、人生观、价值观，体现了高考数学的科学选拔和育人导向作用[2].

1)重视基础知识的考查.对于教材中基础性的核心内容，不论旧教材还是新教材，不管是旧高考还是新高考，每年试卷中都有所考查，例如新高考Ⅱ卷单选题第1～7题、多选题第9～11题、填空题第13～15题、解答题第17～19题，都呈现出对学生基础知识的掌握和对基本的思想与方法运用能力的考查.

2)重视知识本质的考查.例如新高考Ⅱ卷，按照试题设计难度的梯度性原则，单选题第8题难度应适当提高，但本卷仅考查学生对“函数奇偶性”概念的理解，同时，多选题第9题考查学生对样本标准差和样本极差的理解，多选题第11题考查学生对点与圆的位置关系和直线与圆的位置关系概念的理解，通过学生对数学学科知识本质理解深度的考查，达到考查学生数学学科核心素养的目的.

3)重视建模能力的考查.新高考Ⅱ卷通过设计真实问题情境，如填空题第6题以某物理量的测量为背景，考查正态分布基本知识的理解与应用，引导学生重视数学实验和数学的实际应用；解答题第21题取材于生命科学中的真实问题，考查数学抽象、逻辑推理和直观想象等数学核心素养，考查了考生综合运用数学知识和方法解决实际问题的能力，体现了基础性、应用性、综合性和创新性的考查要求.

4)重视素养能力的考查.新题型在新高考中交替出现.新高考内容改革的重要特征就是能力立意到素养导向的转变.一个显著的特点就是在试题结构上增加了多选题和结构不良试题.多选题增加了对知识点考查的广度，出题形式也更加灵活，综合性更强.多选题的引入也为数学基础和能力在不同层次的学生提供了发挥的空间，更加凸显了高考的选拔性功能.结构不良试题能够很好地考查学生对知识体系理解的深度，同时兼顾考查学生思维的灵活性以及对策略的选择能力.例如新高考Ⅱ卷解答题第22题第2)小题是一道结构不良问题，重点考查学生的数学抽象能力、逻辑推理能力和直观想象能力等，体现了素养导向和能力为重的命题原则.

2 命题方向剖析，拓展知识宽度

结合2021年新高考试题的结构特点，本文以解三角形试题的剖析与解读为例，对常与解三角形类问题交叉出题的其他知识进行梳理呈现，希望对一线教师有所帮助.

考向1与棱锥平面展开图结合.

在解三角形与棱锥平面展开图结合类问题中，往往会涉及棱长(夹角)的不变性，即棱锥中的棱长(夹角)与平面展开图中多边形的边长(夹角)相等，有时还会涉及分割平面多边形，在分割后的三角形中，利用正余弦定理进行角边互化或面积公式等基础知识构造方程进行求解.

图1

(2020年全国数学高考试题Ⅰ卷理科第16题)

同理可得

故

在△ACE中，

由余弦定理得

CE2=AC2+AE2-2AC·AEcos 30°

从而

CF=CE=1.

在△BCF中，

由余弦定理得

考向2与有机化学结合.

对于解三角形与有机化学结合类问题，题目往往以空间多边形为载体，利用空间结合体的定义、线线平行、线面平行、线面垂直或面面垂直等相关知识构造辅助线，最后在平面三角形中进行试题求解.一般地，若题目中涉及三角形内切圆半径，则优先考虑面积公式；若题目中涉及三角形外接圆半径，则优先考虑正弦定理；若题目中涉及三角形角平分线，则优先考虑利用面积公式得到边长之间的比例关系；最后若题目中涉及最值问题，则往往利用基本不等式、三角函数等知识进行求解.

例2甲烷是一种有机化合物，分子式是CH4，它作为燃料广泛应用于民用和工业中，近年来科学家通过观测数据，证明了甲烷会导致地球表面温室效应不断增加，深入研究甲烷，趋利避害，成为科学家面临的新课题.甲烷分子的结构为正四面体结构，4个氢原子位于正四面体的4个顶点，碳原子位于正四面体的中心，碳原子和氢原子之间形成的4个碳氢键的键长相同，键角相等，请你用学过的数学知识计算甲烷碳氢键之间的夹角余弦值______.

(2021年全国数学高考高三专题练习题第16题)

图2

易知点E是△ABC的中心，得

在Rt△DEA中，

设AO=DO=x，在Rt△OEA中，

得

在△AOD中，

考向3与现实生活结合.

对于解三角形与现实生活结合类问题，题目多以生活中的文化、事件、场景等为背景，重点考查学生的阅读理解能力、提炼信息的能力和分析与解决问题的能力.该类试题要求学生具备较强的知识迁移和知识的灵活运用能力，因此，在高三复习过程中，教师应有意识地引导学生发现和提出问题，进而增强学生的建模意识和建模能力，最终培养学生利用已学知识建立合适的求解模型的能力，以此达到学生核心素养培养的目的.

例3共和国勋章是中华人民共和国最高荣誉勋章，授予在中国特色社会主义建设和保卫国家中作出巨大贡献、建立卓越功勋的杰出人士.2020年8月11日，国家主席习近平签署主席令，授予钟南山“共和国勋章”.某市为表彰在抗疫中表现突出的个人，制作的荣誉勋章的挂坠结构示意图如图3所示，O为图中两个同心圆的圆心，△ABC中，AB=AC，大圆半径OA=2，小圆半径OB=OC=1，记S′为△OAB与△OAC的面积之和.设阴影部分的面积为S，当S′-S取得最大值时，cos∠BOC=______.

图3

(2021年全国高二数学单元测试题第16题)

解过点O作OD⊥BC于点D，则点D为BC的中点，又AB=AC，故点A，O，D共线.设∠BOC=α，其中α∈(0,π)，则

从而

于是

由f′(α)=0，得

考向4三角形与球结合.

对于解三角形与球结合类问题，往往要利用面面垂直判定和性质定理以及三棱锥中对应的两个垂面分别为等腰或等边三角形，确定三棱锥外接球的球心，结合球心所在平面及外接球性质求出球的半径，最后利用球面积公式求解.有时也会涉及求面积、周长、边长组合、角的正余弦组合等的最值或者范围问题，若是单纯的求最值问题，则可以优先考虑余弦定理和基本不等式；若是求范围问题，则可以优先考虑正弦定理和三角函数，结合角的范围，利用三角函数的图像和性质进行求解；若上述方式无法解决，则可以考虑进行换元构造函数，对函数求导，利用函数的单调性进行解题.

图4 图5

解由题意知：在△ABC,△CBD,△DBA中，

AB2=BE2+AE2，

即

BE⊥AE.

考向5与平面向量结合.

对于解三角形与平面向量结合类问题，该类问题往往涉及平面向量的基本概念(线性运算与几何意义)、平面向量基本定理、向量投影和向量数量积等，以及三角形的“心”(重心、垂心、内心、外心等)的基本概念的理解和相关性质的应用，以此考查学生的转化化归与逻辑推理能力.

(2021年全国模拟预测理科试题第16题)

解如图6，取BC的中点D，联结OD，AD.由△ABC的外心为O可知OD⊥BC.又

图6

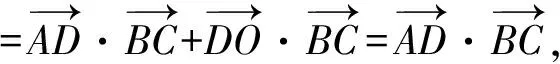
同理可得

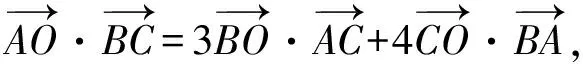
即

亦即

a2+2c2=3b2.

由余弦定理得

考向6与圆锥曲线结合.

解三角形与圆锥曲线结合类问题在往年的高考试题中时常会出现，并且随着新课程和新高考对学生核心素养的高要求以及新高考中多选题和结构不良类试题的出现，这类试题也要引起广大师生的注意.除了要求掌握必备的解三角形相关知识外，还要对圆锥曲线的第一和第二定义、简单性质及离心率e的取值范围等核心知识熟练掌握.同时，对于求离心率范围问题，一般应先将e用有关的一些量表示出来，再利用其中的一些关系构造出关于e的不等式，从而求出e的范围.

解如图7，|PQ|=|QF2|,由|QF1|-|Q1F2|=2a=|PF1|，得

图7

|PF1|=2a, |PF2|=4a.

不妨假设∠F1PF2=θ，则

在△F1PF2中，

得

7a2≤c2<9a2,

即

3 复习建议总结，奠基高考备考

2021年新高考试卷的特点对高考后期的复习、对新高考命题方向的把握将发挥积极的指导作用.在教学中不仅要夯实基础，更要注重对数学本质的理解，突出数学的应用和育人价值，加强思维的训练，提升数学核心素养.

3.1 重视回顾教材，夯实基础知识

数学教材是国家权威专家编写与审查所通过的国家教材，同时也是高考命题的重要参考，因此在高考复习中要回顾教材，夯实基础，对教材中的核心主干知识进行有计划的系统复习，区分和把握好不同层次知识的重点、难度、疑点，由易到难、由浅入深地对基础知识进行系统复习，不能依据“经验”对知识人为地划分重点和非重点、必考点和次考点等，复习要面面俱到，不能出现盲区和盲点，更不能抛弃任何知识点[3].另外，在复习过程中要加强学生对数学概念、定理、性质等知识的本质理解，了解每个知识产生的原因和运用的场景，注重培养学生的数学科核心素养，提高学生综合运用数学知识、思想和方法解决实际问题的能力.

3.2 完善思维过程，提高解题能力

在新高考模式下，突显“小题考方法，大题考运算”的趋势，不同题型对解法的要求也多种多样，但本质都是对数学思维过程的考查.因此，仅有好的解题方法，而没有清晰、严谨的解答过程，很容易出现“会而不对”“对而不全”的现象.因此，在解题过程中一定要做到：1)认真审题：全面、准确地理解题意，挖掘隐含条件，寻找解题突破口；2)完善表达：结合所学知识，构思求解计划，层层深入，步步有据；3)及时回顾：检查求解过程，完善求解漏洞.关注解题过程有利于完善思维品质，提高思维层次，实现良好的解题习惯，从而提高解题能力.

3.3 强调自主学习，提高复习主动性

新高考对学生的阅读理解能力、数学表达能力、提炼信息的能力、知识迁移以及知识的综合运用能力等都提出了很高的要求，因此在高三复习过程中，要培养学生的自主学习能力，养成自主学习的良好习惯.一方面，引导学生进行自主查漏补缺.在复习过程中理清知识要点、难度、易错点，整理和总结易错题，查找复习漏洞，时常进行反思和总结，做到“保强攻弱”，遇到无法理解的难题、错题，应主动地寻求解决方法.另一方面，培养学生多题一解、一题多解和一题多变的思维意识.多题一解有利于培养学生的求同思维；一题多解有利于培养学生的求异思维；一题多变有利于培养学生思维的灵活性和深刻性[4].在分析和解决问题的过程中，既能构建知识的横向联系，又能培养学生多角度思考问题的习惯.最后，强调反思的重要性.解题是学会数学的一个条件，而非关键所在，要真正理解和领悟数学，就必须养成题后反思的习惯.通过反思可以理解数学学科素养的重要性，可以加强对数学问题本质的分析，同时，还能进一步理解数学题型，理解数学思维，理解解题思想.

面对新高考，在高考复习过程中，一方面要夯实基础，循序渐进地推进复习计划；另一方面要注重对数学本质的理解，突出数学的应用和育人价值，强化思维训练，提升核心素养.同时重视培养学生的阅读理解能力、数学表达能力、提炼信息的能力、知识迁移以及知识的综合运用能力等，引导学生探寻数学问题的本质，理清每个问题的思路，做到对多层次知识的融会贯通、灵活运用，最终做到“处事不惊”，以“不变应万变”的心态应对未来新高考的挑战.