概念教学:从起源与发展的角度
李建良 林永伟

摘 要:数学概念在数学学习过程中处于核心地位。数学概念的形成是一个复杂的过程,教师在教学设计与实施的过程中,应追本溯源,关注概念的起源,使学生能形成正确的表象;应循序渐进,逐渐深入地刻画概念的内涵,使学生能拾级而上,直达本质;应适当关注概念的外延,使学生能全面完善地认识概念。
关键词:《面积》;概念教学;概念起源;概念发展
* 本文系浙江省杭州市2021年教师教育科研课题“基于互联模型的小学校本研修的现状和推进研究”(课题编号:JSJY2021003)成果之一。
李邦河院士曾经说过:“数学根本上是玩概念的。”这其实体现了数学概念在数学学习中的核心地位。数学概念的形成是一个漫长的过程,教材中呈现的概念往往经过了长期的凝练,因此具有高度的抽象性。这一方面使得数学概念能够直接反映对象的本质,整体呈现出一种简洁美,但另一方面,也舍弃了一部分对概念的刻画过程,导致学生无法全面、深刻地理解概念。因此,在教学过程中,有必要回到概念的原点,抓住其形成的关键节点,带领学生充分经历和体验概念的形成过程。笔者从概念起源与发展的角度出发,对人教版小学数学三年级下册《面积》一课中的核心概念“面积”进行了教学尝试,以期让学生达成深刻理解。
一、利用生活语言描述概念起源
数学概念不是孤立存在的,在学生认识概念的过程中,相似或相关的概念之间必然会相互影响。这些影响有时会对新概念的形成产生积极作用,有时则会产生混淆,不利于学生理解概念本质。因此,在学生初识概念时,可以有意识地从概念起源的角度将其与相关的概念进行比较与区别,形成概念教学的首因效应。
虽然面积是二维概念,但它与一维的长度概念有着密切联系。小学阶段,各版本教材的编排通常也是先教学长度(包括周长),再教学面积,学生难免会混淆平面图形周长和面积的概念,但面积的教学又很难回避长度。因此,教师可以借助情境,带领学生回到面积概念的起点,结合实际生活经验,帮助学生形成正确的表象,初步体会面积的含义。本节课中,笔者以面积概念的起源——土地测量为素材,把抽象的概念融入生活化的素材中,让学生用生活语言描述他们对面积、长度以及面积与长度的关系的理解,具体教学过程如下:
师:同学们,很早很早以前,人们测量长度用的不是尺子,你知道用的是什么吗?
生:用拃,也可以张开手臂(一庹)或者用脚(一步)来测量。
师:对了,人们常常用脚步来丈量距离。比如说,从家里出发到树林摘果子要走200步,到小河边捕鱼要走150步。后来,人们想要获取更多的食物,你猜他们会怎么做?
生:可以种粮食。
师:是的。如果要在一块长200步、宽150步的地里种粮食,种植粮食的地方大小,与长和宽有关系吗?
生:没有关系,因为庄稼是种在里面的,不是种在长与宽上的。
生:我觉得有关系,虽然是种在里面,但这块地的大小是由长200步和宽150步决定的。
师:结合同学们的意见,长与宽围起来的土地大小,可以叫作它的面积。像这样,物体表面,比如操场、桌面等,或者封闭图形,比如长方形、三角形等,它们的面的大小,就叫作面积。
退回到概念的原点,以生活经验作为学习的起点,用最朴素的语言表达对长度和面积及其相互关系的直观认知,这是一种有别于以往教学中简单堆积实例的教法。虽然学生还不能用数学语言进行准确表达,但从“庄稼是种在里面的,不是种在长与宽上的”“这块地的大小是由长200步和宽150步决定的”等表述中,我们可以发现,学生其实能够模糊地知道面积的概念,并能理解边长和面积之间存在关系。当然,对于概念的形成而言,学生的表述只是表达了他们的直观感受,他们对概念的认识显然还停留在经验层面。因此,要想让学生更加深刻地理解概念,还需要对概念的本质做更深入的刻画。
二、开展多种活动刻画概念本质
对数学概念的理解不能停留在表面,想要真正理解和掌握某一数学概念,就要准确把握概念的各个要素,以及要素之间的联系。这就需要基于学生已有的认知和经验,设计不同层次、不同侧重点的学习任务,引导学生在一系列观察、比较、分析、概括等感知和思维活动中,深入挖掘概念的本质内涵,提炼、总结出所学概念的本质特征,这是概念学习的关键环节。
面积概念的形成,既要注重结果,也要关注过程。也就是说,我们最终要让学生能以恰当的方式表示给定图形的面积大小,同时也必须让他们了解得出这一结果的过程和方法,并体会其中蕴含着的面积“有限可加性”(所求图形面积是单位面积的累加)。本节课中,笔者设计了一系列活动,将面积的这一属性多次运用到图形的面积测量或计算中,引导学生在活动中经历概念的发生与发展过程,逐步剥离概念的非本质属性,深入挖掘概念本质。
(一)活动一:感受长度与面积的联系
教学中要充分利用概念之间的联系,将学生的已有经验化作概念学习的助力。教学“面积”前,学生已经具备了对长度“有限可加性”的认知,这对面积“有限可加性”的理解具有正迁移作用。笔者设计了“比较一条边长相等的两个长方形(正方形)的大小”的活动,学生在解决这一问题时,只需考虑另一条边的长度与面积的大小关系,从中感受面积与边长的联系。活动过程如下:
师:同学们,老师这里有两块地,①号地是长16步,宽16步的正方形;②号地是长32步,宽16步的长方形。这两块地谁大谁小?
生:把两块地叠在一起就可以比了。
生:因为它们宽是一样的,①号地长16步,②号地长32步,所以②号地更大。
(二)活动二:比较长度与面积的区别
在学生借助已有经验初步研究概念后,教师需设法帮助学生突破原有认知的束缚,让学生的注意力快速转向探求新概念的本质属性。笔者组织学生比较长、宽各异的两个长方形的面积,学生无法像之前一样直接对比,从而引发他们对边长与面积关系的思考,催生了寻找、运用新的测量工具或单位的需要。活动过程如下:
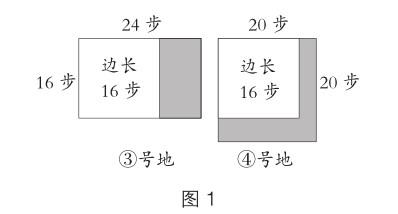
师:(出示:③号地长24步、宽16步,④号地边长20步)现在,比一比③号地和④号地的边,能不能直接看出谁大谁小?
生:不能,③号地的长比④号地的长要长,但宽比④号地的短,很难说谁大谁小。
生:可以用一个小正方形量一量。
师:如果用刚才的①号地来量,你发现了什么?
生:(出示图1)用①号地量③号地还剩一点,量④号地也还剩一点。但是剩下的也看不出谁大谁小。
(三)活动三:选择恰当的度量单位
学生对概念的本质有了初步的认识后,教师应有意识地制造认知冲突,激发学生进一步探究的意愿。在测量不同长方形的面积时,学生必然会想到用多种单位面积去测量,也就必然面临单位面积的选择问题。学生选用不同的单位面积,应产生于解决问题的实际需要。因此,笔者设计了测量长方形面积的活动,加深学生对“图形面积是单位面积的累加”这一本质的理解和对单位面积之间的关系的体会。活动过程如下:
师:用①号地来量也依然无法判断,但你有没有从中获得什么启示?能用什么办法来对比③号地和④号地的大小呢?
生:用再小一点的正方形,补在旁边空缺的地方就可以了。
(教师提供边长8步和边长4步的小正方形学具,学生开展小组合作探究后汇报。)
生:③号地我们用边长8步的正方形来量,一共用了6块。
生:④号地我们用边长8步的正方形量,用了4块,还有多余,再用边长4步的正方形来量,用了9块。
生:我们小组刚才量之前先比了比,发现4块小的(边长4步的正方形)和1块大的(边长8步的正方形)一样。所以④号地就等于6块大的加1块小的,比③号地多1块小的。
(教师根据学生描述,同步在黑板上拼贴板书,最终形成图2。)
生:我们是直接用边长4步的正方形去量④号地,发现刚好可以量完,用了25块。
生:③号地也可以全部用边长4步的正方形去量,一共要用24块,比④号地少1块。
教师只有结合具体教学内容,对概念形成机制进行深入解读,并准确把握学生的学习规律和认知心理,才能引导学生循序渐进、稳步扎实地形成数学概念。这一系列活动是在教材提供的素材和思路的基础上的进一步细化,体现了概念形成和发展的过程性和层次性。学生在活动中独立观察、交流思考、深入理解,自主发现了单位面积之间的倍数关系,也为后续学习国际标准面积单位之间的进率与转换铺垫。
三、借助实际问题拓展概念外延
概念的内涵比较抽象,学生认识了概念的内涵,并不意味着完全掌握了概念。小学生倾向于用直观、具体、形象的表象帮助理解和记忆,并在头脑中对这些表象进行加工,从而化繁为简、加深理解。也就是说,学生头脑中积累的正确表象越多,就越容易发现其中的规律。因此,要想让学生全面认识、深入理解概念,还需要适当拓展它的外延。教学中,除了举例等直接呈现的形式外,还可以让学生运用概念解决相关问题,逐步达成拓展概念外延的目的。
考虑到数学知识本身的系统性,本节课有必要引导学生进一步探究并形成对单位面积的认知体系。为此,笔者为学生提供了若干个长方形作为被测量对象,促使学生不断创造新的单位面积,并自主形成单位面积体系。具体教学过程如下:
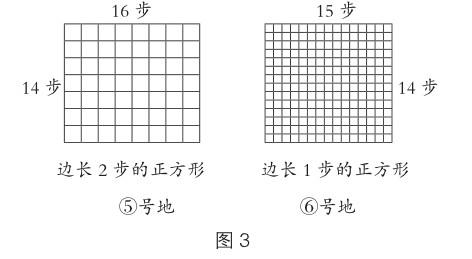
师:(出示:⑤号地长16步、宽14步,⑥号地长15步、宽14步)这两块地还能用边长8步的正方形来完整地测量吗?边长4步的呢?
生:⑤号地不能用边长8步的正方形量,横着可以放两个,竖着放一个还有剩余;也不能用边长4步的正方形量,14除以4除不尽。
生:可以用边长2步的正方形量,一行放8个,有7行。
生:⑥号地不能用边长8步或4步的正方形量,2步的也不行,可以用更小的,比如边长1步的正方形量。
(课件演示测量⑤号地和⑥号地的过程,如图3。)
师:刚才同学们创造了边长分别为8步、4步、2步、1步的正方形来测量这些长方形。你喜欢用大的正方形还是小的正方形来量?
生:我喜欢用大的正方形,量起来快。
生:我喜欢用小的,小的可以量各种各样的长方形。
生:其实它们各有优点和缺点。大的量起来方便,但常常会有多余;小的可以量各种长方形,但是数个数有点麻烦。
师:你的评价非常公正。是的,为了测量不同的长方形,我们应该根据实际需要灵活地选择不同大小的正方形作为测量单位。
学生在解决实际问题的过程中,进一步创造新的单位面积,形成了较为完整的单位面积体系,扩大了面积和单位面积概念的外延。学生在评价不同单位面积的过程中,进一步深化了对单位面积的价值的理解,对面积和面积的测量有了较为全面的认识。学生在感受到“面积大小”可以用“正方形的个数”来描述时,自然实现了对面积本质的高度抽象和概括,建构了面积单位的意义,因此,笔者在教学时并没有指出“通常用边长为1个单位的正方形作为面积单位”,而是让学生“灵活地选择不同大小的正方形作为测量单位”。
概念教学中,要带领学生经历“直观描述概念—刻画概念本质—丰富概念外延”的过程。在这些过程中,教师应尽可能为学生创造更多独立思考、操作体验、交流互动、应用拓展的机会,为数学概念在学生心中扎根提供肥沃的土壤。
参考文献:
[1]萧恩颖.顺应认知规律 调整学习序列——基于“量感”形成的“面积”单元整体设计与教学实践思考学[J].教学月刊·小学版(数学),2021(3).
[2]杨凤萍.概念在探究中深度建构——基于沪教版三上“面积”的教学实践与思考[J].小学数学教师,2021(11).
(李建良,浙江省杭州市萧山区夹灶小学,邮编:311247;林永伟,副教授,杭州师范大学继续教育中心,邮编:311121)

