一致性理论优化无人机集群编队控制

徐 珂，王建林，2

（1.国网山东省电力公司菏泽供电公司，山东 菏泽 274000；2.吉林大学软件学院，吉林 长春 130000）

1 引言

无人机系统在航迹规划、机车避障等方面取得了大量的研究成果，并逐渐转向多无人集群系统平台。多无人机集群平台在发挥平台间互协作提高工作效率的同时，极大增强的系统的容错和抗干扰能力[1]。多智能体系统一致性协同控制[2]通过合适的局部信息协作控制构建分布式控制器使多智能体的某个状态趋同或达到共同值的动态过程，在多无人系统的分布式优化编队飞行等领域得到广泛应用。

文献[3]根据MAS一致性控制理论，在无人机队形设计控制中增加领导者信息获取和控制，在部分无人机获取领导者状态信息情况即可实现全队形的编队控制。文献[4]引入虚拟领导者组成时变多智能体固定拓扑结构，并通过跟踪误差修改控制率，实现了无人机编队飞行及避障。文献[5]采用线性二阶模型对无人机集群系统进行建模，探讨了平均一致性在无向通信拓扑下的控制问题。文献[6]以二阶积分模型描述四旋翼无人机集群系统，并采用图论分析集群编队的一致性控制。文献[7]融合多机避障方法与一致性控制理论，设计编队控制以避免编队与障碍物发生碰撞并生成期望的控制编队。

已有研究成果多是基于一阶、二阶积分模型，集群的通信拓扑采用无向图进行分析。由于干扰及距离限制等因素的存在，集群间的无人机通信通常为单向并表现出明显的非线性特性[8]，因此有向拓扑和非线性控制的研究更贴合实际应用情况为此，基于有向拓扑建立了集群的二阶离散模型，设计了分布式控制协议，通过理论分析和推导，得到了实现期望集群编队的约束条件，最后采用经典二阶积分模型对算法模型和控制协议进行仿真，验证了模型的有效性。

2 有向通信拓扑图理论

设无人机集群系统有编号为1,2,…,N的N架无人机组成，如果将各机视为一个图节点，则集群的拓扑结构可以描述为有向图G=(Ω,ε,A)，式 中Ω={1,2,…,Ν}为 集 群 的 节 点 集，ε={e0:i,j∈Ω}为边集，A=[aij]N×N为有向图邻接矩阵，用于描述边集的连接权重。在以有向图表示的无人机集群中，如果某无人机i的状态信息可以通过拓扑网络被另一无人机j接收，即在G中两无人机节点间存在向向边eij∈ε(i≠j)，则称j为i的邻居，即Ni={j|j∈Ω:eij∈ε}。如果存在一个节点i，可以通过非零的有向边将其状态信息传递到拓扑结构图中的任意其他点，则称G包含了一个有向生成树[9]。图的Laplacian矩阵L=[lij]N×N，则有：

当有向拓扑图G的Laplacian矩阵L具有非负特征值及至少一个零特征值，且他非零特征值均正实部，则当G中存在一个有向生成树时，零是L矩阵的1重数特征值；当且仅当G中存在有向生成树，有谱半径u=ρ(G)对应的特征值为1n，则u为G和单重特征值，则对于任意给定的x,y∈Rn以及具有相容维数的矩阵P>0，D和S，可以得到

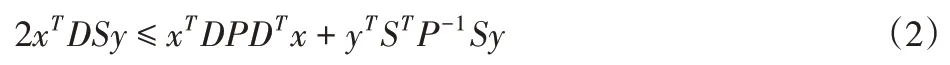
3 基于一致性理论的集群控制

将文中N架无人机集群通信结构描述为包含向生成树的有向图G。设集群为单机动态特性相似的非线性时不变同构系统，则无人机集群中第架无人机节点的动力学模型为：

式中：xi(t)∈Rn、vi(t)∈Rn—无人机相应的位置、速度；ui(t)∈Rn－控制输入；δ—状态信息采集时间周期，状态更新t=t0+qδ；t0—采样初始时间；n—集群的空间维数。则集群系统的数据模型可以建模为[10]：

式中：ξi(t)=[xi(t)，vi(t)]T；B1=[1，0]T、B2=[0,1]T—维数相容的常数矩阵。

设h(t)=[hT1,hT2,...,hTN]T∈R2N为描述集群队形的一组编队参考向量，hi(t)=[hxi(t),hvi]T，hxi(t)和hvi分别为编辑参考位置与期望速度向量，根据多智能体一致性理论和无人机与其局部邻居之间的相对状态信息及通信拓扑，则期望的分布式集群编队控制器可以采用有界函数描述为：

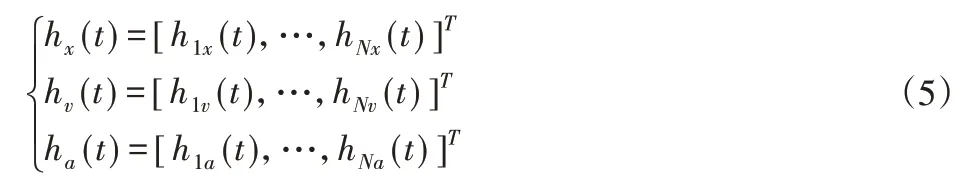
其闭环系统方程可以推导为：

式中：i=1,2,...,N，K—系统的反馈增益矩阵，c>0—耦合系数，F(x)—Lipschitz非线性函数。

根据文献［5］中分析，如果无人机集群系统中任意两个节点i，j=1，2，...，N，i≠j，及有限初始值xi(0)，使式（7）成立，即：

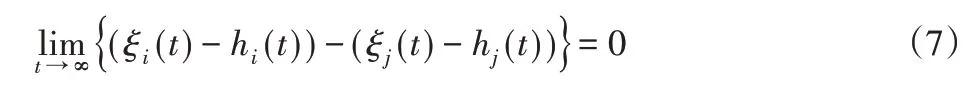
式中：i，j=1，2，...，N，hi—无人机的状态信息，用于描述多无人机系统的编队队形，则该集群系统实现了期望编队h[11]。

当输入控制ui使得无人机集群实现了编队h(t)的期望，则h(t)在协议ui下是可行的。

根据文献[11]中的分析，为使无人机集群达到期望的控制编队队形，基于一致性理论，分布式控制协议为：

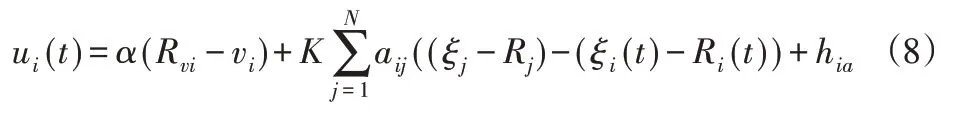
式中：α，β>0—增益系统，K=[−α，−β]—待设计控制参数。

通过一定的补偿策略，可以将式（8）中的非一致时延补偿为一致性以消除其对通信拓扑的影响。

4 集群系统分布式编队控制

文中将无人机集群系统的通信拓扑及时延描述为含有向生成树的非线性有向图，并通过变量替换将上节式（8）描述的编队分布式一致性控制可以转化为系统的稳定性求解问题。

令ψix(t)=xi(t)−hix(t)，ψiv(t)=vi(t)−hiv(t)，将其代入式（8）和式（3），则无人机集群的动力学模型可以进一步转化为表示为：

定义单位向量E和E−1分别为：

则式（9）可进一步推导为：

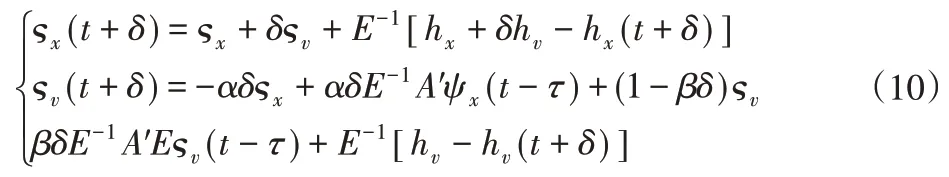
其中，ςx(t)=E−1ψx(t)，ςv(t)=E−1ψv(t)，A′=[a′ij]N×N。

同时根据式（10）可以得到有：

则根据式（7）编队满足h队形的控制条件，当式（10）的编队相对误差对任务初始条件，有ς(t)→0(t→∞)，则式（8）描述的控制协议可以确保非线性无人机分布式编队控制满足hvi，即有：

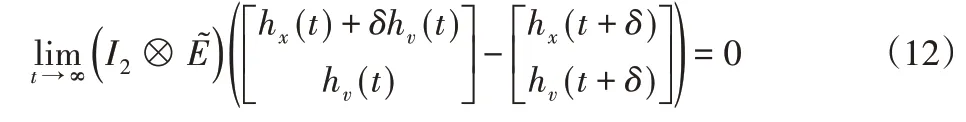
令K=BTP2，P2—正定矩阵，同时期望的编队队形h符合(E⊗A)h=0，则可以推导出：

设ϑ1和ϑ2为矩阵的最大特征值和最小特征值，则有正定矩阵P1≤ϑ1I，P1≥ϑ2I，从而可进一步推导得到：

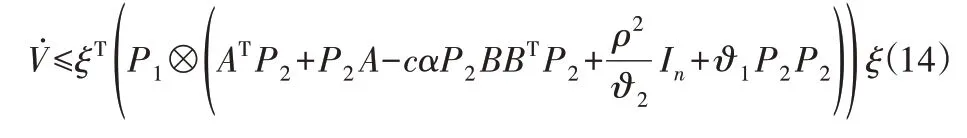
式中：c>0，由式（14）不等式条件可进一步得到，无人机集群可以形成编队h时，当且仅当满足式（15）条件。

式（15）条件描述大式（8）所示控制协议下，集群实现期望队形的约束条件，说明需要在集群位置、位置及控制输入等“相容”情况下，集群可以达到期望编队。

5 仿真实验与结果分析

5.1 仿真条件及参数设置

采用4架无人机组成这里实验采用的仿真集群，无人机在二维平面运动并采用经典二阶积分系统模型，非线性函数项为f(xi,t)=[0,0.1 sin(xi2(t)),0,0]T，实验中位置，速度和加速度单位分别为m、m/s、m/s2。无人机通信拓扑结构，如图1所示。

图1 无人机之间的通信拓扑结构Fig.1 Communication Topology between Drones

可以看出，拓扑结构对应的图是有向且含有一个生成树，集群无人机的初始位置为：

期望编队队形为间距100m的正方形队形，则编队描述为h=[hix(0),hiv(t)]，即

结合给定的初始条件，通过迭代计算，可以得到不同时刻的期望队形，迭代结束后，可以得到队形满足(E⊗A)h=0，且根据约束条件，可以得到参数α=0.19，β=0.61，δ=0.15。

5.2 仿真结果及分析

通过层高差来避撞的无碰撞参考的控制协议下，得到的实验无人机集群运动轨迹并形成期望编队的过程，如图2所示。图中坐标为集群在形成编队过程的x和y方向的位置，矩形框为四架无人机之间的相对位置，可以看出，从开始位置，大约经过100s的时间，集群初步完成队形，之后保持较好的期望队形运动。此验证了结论的正确性。

图2 无人机集群系统编队队形形成过程Fig.2 UAVs Formation Realization Process

集群中四架无人机的速度和随时间变化的仿真结果，如图3、图4所示。可以看出，在仿真实验初期，无人机之间以不同的速度趋向相应的位置，当到达期望位置后，各无人机保持稳定的相对速度，这与算法分析一致，而形成编队后，各无从机之间的位置也保持了固定的相对距离。同时拓扑图还反映出无人机1不能获取另个三架无人机的状态信息，只能传递自身状态信息，因而可看作领航者，其他三架无人机可看作是跟随者。

图3 无人机速度随时间的变化趋势Fig.3 The Velocity Trends of the UAVs over Time

图4 无人机位置随时间的变化趋势Fig.4 The Position Trends of the UAVs over Time

综合所有实验的仿真结果可以得出，设计的集群编队控制协议能够何足挂齿无人机快速趋向期望队形，并在形成编队后，能够保持较好的相对位置和速度。

6 结论

利用多智能体一致性理论研究了在有向通信拓扑结构下，无人机集群的分布式非线性编队控制问题，建立了集群的二阶离散模型，设计了分布式控制协议，解决了具有Lipschitz非线性特性的的无人机分布式编队问题；通过理论分析和推导，得到了实现期望集群编队的约束条件，最后采用经典二阶积分模型对算法模型和控制协议进行仿真，验证了模型的有效性。