机器混合故障下柔性作业车间鲁棒调度方法
侯娅楠,袁逸萍,巴智勇,李 明
(新疆大学机械工程学院,新疆 乌鲁木齐 830047)
1 引言
柔性作业车间调度问题(Flexible job shop Scheduling Prob‐lem,FJSP)的特点是每一道工序的可选加工机器可能不唯一,相比传统车间调度更加符合车间生产实际。然而在实际生产中常存在机器故障、紧急插单等多种不确定因素。机器故障作为主要的不确定因素,常导致实际生产和计划产生偏差,并引起物料配送等相关生产环节的混乱,对生产过程带来重大影响[1]。面对机器故障影响,如何制定出具有抗干扰能力鲁棒性调度方案已成为生产调度研究的一个热点。调度的鲁棒性指调度在不确定环境下保持原有状态或性能的能力,通常分为质的鲁棒性和调度稳定鲁棒性[2]。
实际制造车间机器包含退化故障与突发故障两种失效模式[3]。因此在制定调度方案时考虑未来机器退化故障与突发故障干扰,研究机器混合故障下的柔性作业车间鲁棒性调度问题对于现实车间调度计划的制定与执行具有重要指导意义。
针对机器故障这一不确定因素,国内外学者做了大量研究,文献[4]通过设计编程算法来插入空闲时间以应对随机故障对调度的扰动;文献[5]为提高调度鲁棒性提出了不同的空闲时间插入策略;文献[6]分析了机器随机故障问题对多目标柔性作业车间调度的影响。
上述方法是通过插入缓冲时间的方式来增强调度的稳定性。另一种方法则是鲁棒性替代测度方法,文献[7]结合流水车间的特点,采用前摄优化理论,设计鲁棒性代理指标和对应算法;文献[8]考虑机器负载与故障的相关性,设计相应测度来近似调度方案的鲁棒性。文献[9]提出了相对偏差鲁棒性指标和考虑空闲时间与负荷关系的鲁棒性指标。除此之外,部分研究发现预防性维护(Preventive Maintenance,PM)可以有效防止机器发生退化故障,并在单机[10]、流水车间[11]、柔性作业车间[12]做了大量应用。
研究多涉及机器退化故障对调度鲁棒性的影响,未综合考虑退化故障和突发故障的混合作用对于调度鲁棒性的影响,研究机器混合故障下的鲁棒性调度方法对实际生产的指导更具全面性。预防性维护是根据机器的退化故障施行的,可有效改善机器的故障发生率,但无法完全避免故障的发生。
将混合故障拓展至柔性作业车间,同时考虑机器的退化故障和突发故障,根据机器因加工造成的退化故障制定预防性维护,对机器的突发故障添加适量缓冲时间,综合考虑调度质和解的鲁棒性,提出自适应预防性维护与缓冲插入策略,设计有效算法对集成调度问题求解,为车间提供更加稳定的调度方案。
2 混合故障下鲁棒调度方法
2.1 混合故障描述
车间中机器发生的故障类型包含退化故障和突发故障,一般认为这两种故障的失效函数服从不同参数的二参数威布尔分布[2],该分布的概率密度函数,如式(1)所示:
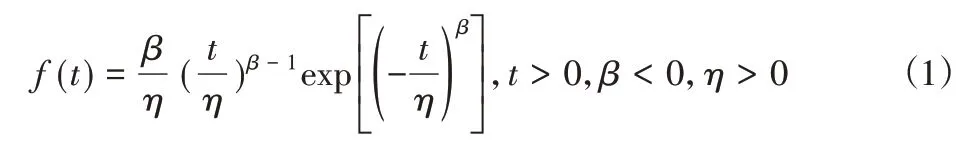
式中:t—机器运行的第t时刻;β—形状参数;η—尺度参数;二者与机器使用时间t无关。
机器在t时的刻退化失效模式下的可靠度,如式(2)所示:

机器在t时的刻突发失效模式下的可靠度,如式(3)所示:

2.2 基于退化故障的预防性维护添加
采用预防性维护可降低车间机器发生退化故障的概率,考虑到机器的退化可靠度约束,为方便计算,将可靠度维度转化为时间维度,对式(2)做转换可到式(4),可计算当机器达到可靠度阈值时对应的机器役龄Zk′。

式中:Rk′—可靠度阈值。
进而在役龄阈值处添加预防性维护活动,需要说明的是生产调度初步生成时,因工序约束和机器约束,导致计划本身含有空闲时间。因此,预防性维护时段添加策略如下:
判断预防性维护的位置状态。若在加工连续的序列中,这时在此工序前直接插入,后续序列向右后移,以防止机器的可靠度超出阈值;若处于较小空闲时间中,则不能够完全容纳正常维护活动所需时间,需向右扩充,后续序列向右移动;当在完全空闲时间中,安排在前一工序之后,不影响后续加工任务。
2.3 基于机器突发故障概率的缓冲时间插入
针对车间机器不可避免的突发故障,基于机器突发故障概率,在每一道工序后加入一定的缓冲时间,以吸收机器突发故障对于调度计划的干扰。
机器k加工oij时发生突发故障的概率p[ijk]如下:

式中:aij—工序oij开工时机器k的役龄;bij—工序oij完工时机器k役龄。
机器k加工oij时发生突发故障插入的缓冲时间I[i,j,k]如下:
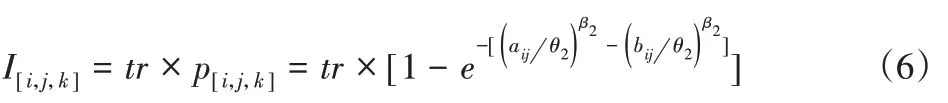
式中:tr—平均修复时间。
由于工件的工艺约束和机器约束,导致调度计划中产生无法避免的空闲时间。在缓冲时间插入过程中,采取阈值法进行灵活插入。当所需缓冲时间小于自有空闲时间,则在当前工序后插入缓冲。否则,不做插入操作。
3 问题描述与模型求解
3.1 柔性作业车间问题描述及假设
FJSP包含n个工件和m台机器,各工件包含i道工序,每道工序可在一台或多台机器上加工,对应的加工时间可能不同。
对所研究内容做以下假设:
(1)工件的加工工艺流程是已知的;
(2)机器故障只发生在机器加工期间,修复后可继续加工;
(3)机器发生退化故障或突发故障均采取小修,但小修时间不同。小修仅使机器恢复运转,不改变机器的可靠度;
(4)预防性维护不可中断当前工序。
3.2 数学建模

表1 符号表示及其说明Tab.1 Symbol Representation and its Description


式(7)表示目标函数,为质的鲁棒性值与解的鲁棒性值的线性加权组合,α1+α2=1;式(9)~式(10)表示在预测调度中的工序开始时间和完成时间对应的工件工艺约束和机器加工约束;式(12)为机器的可靠度约束;式(13)~式(14)为混合故障下实际调度的工序的加工时间约束;(16)表示工序和机器一一对应;式(18)表示实际最大完工时间。
3.3 求解算法
采用改进的遗传算法来进行模型求解,算法步骤如下:
(1)参数初始化,采用随机初始化方法,基于工序和机器编码方式,生成初始种群;
(2)考虑机器的可靠度约束,在种群染色体编码中自适应的加入预防性维护序列,得到柔性作业车间预防性维护调度;
(3)基于机器突发故障率,计算缓冲时间插入量I[i,j],插入缓冲时间序列,得到预防性维护鲁棒调度;
(4)随机生成随机数rand,如果rand大于退化故障概率,故障矩阵中对应元素为1(发生退化故障),若rand 大于突发故障概率,则矩阵对应元素为2(发生突发故障),如果同时满足则随机生成1或2。最终生成混合故障矩阵;
(5)计算种群个体在混合故障下的鲁棒性值,进行概率分配与适应度排序;
(6)判断是否达到迭代次数。得到调度模型最优解,结束。否则执行(7);
(7)对种群进行遗传操作(选择、交叉和变异),生成新的种群,继续执行(2)。
算法具体操作,如图1所示。

图1 算法流程图Fig.1 Framework of the Algorithm
3.3.1 染色体编码与解码
由于FJSP中各工序可选加工机器不唯一,要解决的问题包括:确定工序的机器选择;确定各机器工序的加工顺序;确定预防性维护位置;确定缓冲大小和位置;因此采用基于工序和机器的四层编码方式,染色体编码方式图,如图2所示。
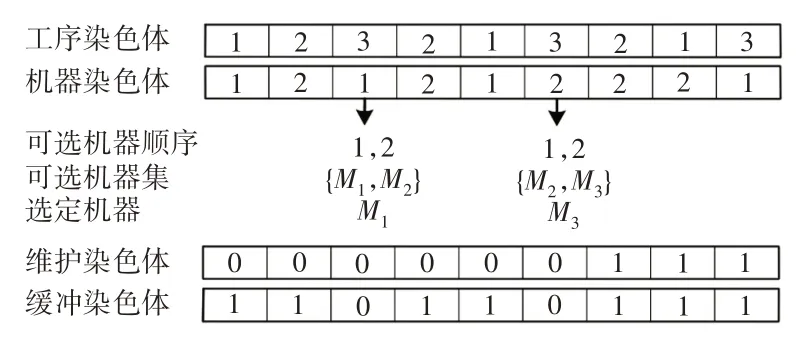
图2 染色体编码方式图Fig.2 Chromosome Coding Pattern
现有3台机器,3个工件,且每个工件包含3 道工序。
工件号出现的次数表示对应工件的工序号,如第一个3表示工件3的第一道工序,其对应的机器码为1,则在可选机器集{M1,M2}的第一个机器上加工,即在M1上。
染色体先由工序序列和机器序列组成,考虑到机器的可靠度约束与突发故障概率,对初始染色体进行扩充,转变成由工序、机器、维护和缓冲时间序列四部分组成的新染色体,染色体长度为工序总数的四倍。
图2中维护染色体的三个1分别表示在o23、o13、o33后添加预防性维护。相应的缓冲染色体基因为1表示在对应工序后添加缓冲时间,为0则不添加。工序染色体、机器染色体、维护染色体和缓冲染色体4部分编码构成一条完整染色体,即所求柔性作业车间问题的一个可行解。
3.3.2 个体的适应度函数和初始种群
适应度函数是种群个体优劣评价的关键,采用适应度函数非线性排序法进行个体适应度评价,适应度值函数如下:

按上述适应度值计算方法对种群中个体成员进行降序排列,进而分配概率。此时,概率则表示种群个体的适应度值即新的个体适应度值。
4 数值实验与分析
为验证同时考虑退化故障与突发故障两种失效模式的混合故障下鲁棒性调度方法和算法可行性,做相应测试。
选取柔性作业车间基准案例9 个,分别是Brandimarte 设计的3个案例(mk01、mk04、mk05)和hurink设计的6个案例(mt06、mt10、mt20、la01、la06、la11)。根据问题特点,结合文献[11],适当调整算例参数,涉及的调度参数包含退化失效与突发失效对应的形状参数β、尺度参数η、故障持续时间tr,机器维护时间tp,取值,如表2所示。机器的可靠度阈值Rk′=0.85,通过式(4)可得对应的役龄阈值Zk′=20.16。

表2 调度参数Tab.2 Scheduling Parameters
将此调度方法分别与传统调度方法和考虑预防性维护的调度方法进行比较。在传统调度方法中,模型考虑退化故障,用工序加权总松弛时间之和来衡量调度方案的鲁棒性,不考虑加入缓冲时间[8]。在考虑预防性维护的调度方法中,工序调度与预防性维护联合决策,且不考虑加入缓冲时间[12]。
设置种群规模为300,交叉率为0.7,变异概率为0.1,迭代次数100。程序使用Matlab2014b,在8G内存、2.40GHz的CPU上运行。利用第3节step4的方式产生5000组机器混合故障实例,对三种方法所得的调度的最优调度解进行测试。
为体现算法的稳定性,将算法运行20次取平均值。分别记传统调度、维护调度和所提鲁棒性调度的质的鲁棒性指标依次为MP1、MP2和MP3,解的鲁棒性指标依次为MR1、MR2和MR3。计算结果,如表3所示。可以看出鲁棒性调度解的期望完工时间略微高于其他两种调度方法,然而工序完工时间偏差总和确远低于MR1和MR2。

表3 三种方法的鲁棒性指标比较Tab.3 Comparison of Robustness Indexes of Three Methods
为了更好的定量评价本文调度方法的改善程度,采用GJL(改进率)来衡量算法的有效性,TtP+R、TpP+R、TrP+R分别表示三种方法的解的总目标函数值,GJL1−MP=(MP3−MP1)/MP1表示鲁棒性调度方法相对于传统调度方法在质的鲁棒性上下降的百分比。GJL1−MR=(MR3−MR1)/MR1则表示相对于传统调度方法在解的鲁棒性上下降的百分比。所提方法相比传统调度方法在综合鲁棒性指标上的改善程度用GJL1−TP+R=(GJL1−MP+GJL1−MR)/2表示,同上可得相对于预防维护调度方法的改进率GJL2−MP、GJL2−MR、GJL2−TP+R。
表4给出了当α1=0.5,α2=0.5时,三种算法得到的数据结果。根据表4中数据可得,鲁棒性调度解相比传统方法和维护调度虽然在质的鲁棒性改善程度上下降了平均4.6%和2.2%;但却使调度解的解的鲁棒性提高了大约45.7%和30%,在总目标上分别改善了25.2%和16.1%。这说明考虑维护与缓冲的鲁棒调度方法对于机器混合故障所造成的工序加工时间波动具有一定的免疫功能。还可以发现随着案例规模的增加,改善程度也相对增加。

表4 不同规模案例的结果对比Tab.4 Comparison of Results in Cases of Different Sizes
案例Mk01使用所提鲁棒调度方法求得的最优鲁棒性调度解,案例包括6台机器,10个工件,共计55道工序,如图3所示。编号601为工序编号,表示6号工件的第1道工序。PM为各加工机器的预防性维护工作,灰色矩形方块为工序后所添加的缓冲时间。

图3 Mk01最优调度解甘特图Fig.3 Optimal Scheduling Solution Gantt Diagram of Mk01
5 结语
将机器在生产运行中发生的混合故障引入到柔性作业车间鲁棒性调度问题的模型中,综合考虑质的鲁棒性与解的鲁棒性指标,通过算法对机器预防性维护、缓冲时间和车间调度进行了有效的集成与优化,最终得出柔性作业车间鲁棒调度方案。对多个不同规模案例的测试验证了所提鲁棒性调度方法是有效的,综合指标的改善程度相对传统调度与预防性维护调度较大,且随着问题规模的增加,改善程度也相应提高。后期将深入研究机器混合故障下的鲁棒性替代测度,以及混合故障环境下作业车间重调度时机和策略。

