细胞分析仪取液系统的改进型FORM算法可靠性评估
姜振海,黄炜祺,谷东伟,郭训薇
(1.长春工业大学机电工程学院,吉林 长春 130012;2.南京华群光电技术有限公司,江苏 南京 210000)
1 引言
加速寿命试验是验证复杂机械系统可靠性的重要方法,如何进行加速寿命试验,如何在短期内获得有效的试验数据,如何有效的依据数据进行可靠性评估就显得至关重要。
国内外关于加速寿命试验的研究最早可以追溯到62 年前Levenbach 发表的论文《电容器的加速寿命试验》[1];随着加速寿命试验理论的成熟,通过对现代航空发动机轴承进行全尺寸的加速寿命试验[2],获得导致轴承异常失效的原因,并通过对正在运转的设备进行寿命评估的方式[3],提出在温度循环环境下的试验方法以及测试结果;在对潮汐涡轮叶片进行加速寿命试验[4]中,提出在四种不同应力水平下,潮汐涡轮叶片在积累损害的同时,对设备的寿命进行研究;三脚架式CVJ加速寿命试验[5]中发现粘着磨损现象,提出一种新的磨损寿命模型并结合运动学分析,验证加速寿命试验中所建运动模型的正确性;通过火炮的精度以及寿命研究,提供一种加速寿命试验的研究理论[6−7],通过分析加载力、运行速度及额定动载荷,定义单因子及双因子应力试验的形式,明确加速因子、加速模型、误差范围以及加速寿命试验步骤。
为进行可靠性评估,加速寿命试验中常用到的方法有FORM(Fist−order reliability method)算法[8−13]、SORM(Second−order reli‐ability method)算法[14−15]、MC(Monte−Carlo)算法[16−18]。
FORM算法主要从模型的结构角度寻找极限状态函数,根据变量确定函数曲线的维度,为寻找可靠性指标提供验算点,但获得的验算点误差较大,可靠度值存在较大争议。
SORM算法主要从寻找极限状态函数的曲线并进行二次求导,促使验算点处的精度更高,误差更小,但验算点处的灵敏度过高。
MC 算法主要从大数据角度出发,针对模型的失效数据,通过伪随机数的方式进行数据扩充并大量抽样,为失效概率提供依据,尽管计算结果误差小,但计算成本、所需样本数高;此外,在MC算法的基础上还运用MCMC技术[19]提高计算机模型的可靠性和准确性以及根据随机变量在概率密度函数中可能遵循多模态分布这一特点,提出一种高精度概率不确定性传播方法[20],当涉及多模态分布时,计算误差较小,但计算难度大,不适用于实际工程中;以上几种可靠性算法在进行可靠性评估时,会存在验算点位置精度低、验算点灵敏度高、计算成本高等问题,导致可靠性指标误差变大、耗时长等状况出现,从而降低设备可靠度。
由于改进型FORM算法能够定位验算点位置,降低验算点的灵敏度,并且所需样本数少,还能对加速寿命试验所得出的失效数据进行优化分析,因此本文通过改进型FORM算法对细胞分析仪取液系统机械传动结构的加速寿命试验进行可靠性评估。
首先,通过分析设备的材料以及相关特性,确定加速模型和应力模型。
然后,利用加速寿命试验与ADAMS 仿真技术相结合,针对易失效部件进行虚拟样机技术仿真。
最后,改进FORM算法对加速寿命试验得出的失效数据进行优化,减小误差,提高可靠度。
2 加速寿命试验与动力学仿真
由于取液系统机械传动结构是细胞分析仪的重要组成部分,其可靠性直接影响细胞分析仪的使用效率,所以,针对加速寿命试验以及动力学仿真,需要建立取液系统机械传动结构三维模型并通过ADAMS(Automatic Dynamic Analysis of Mechanical Sys‐tems)进行模型处理以及应力分析,进而获得应用于可靠性评估的失效数据。
2.1 加速寿命试验与应力分析
为实现加速寿命试验以及动力学仿真,首先通过CATIA 建立取液系统机械传动结构模型,其机械结构模型,如图1所示。
将模型导入ADAMS进行干涉检查,通过布尔运算合并相同材质元件;并对运动部件进行运动副约束。
在ADAMS 中选取同步带系统,并添加驱动及应力载荷,如图2所示。

图2 X、Y轴同步带添加载荷Fig.2 Load Addition for Synchronous Belt of X and Y Axes
依据早期设备的故障数据进行分析,取液系统机械传动结构的失效形式主要是同步带断裂,由于同步带的故障基本属于疲劳磨损,其疲劳寿命符合对数正态分布,因此选取公式(1)逆幂律模型进行加速寿命试验分析。

式中:a,b—待估参数;φ(Pi)—应力函数;ui—疲劳寿命的对数均值。针对逆幂律加速模型,在标准环境下,室温25℃,相对湿度55%RH,标准大气压101Pa。
加速因子的计算方法如式(2):

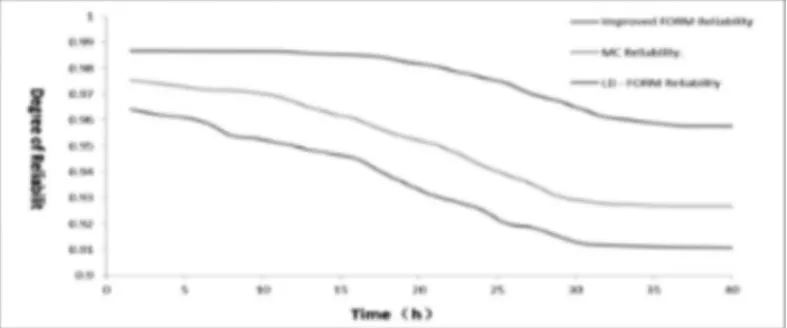
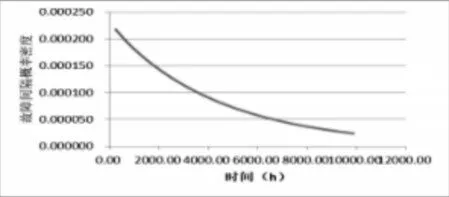
式中:m—加速率常数,2 其中关于m的取值,一般电容器以直流电压V加速,m=5;滚珠轴承及钢材的断裂,m=3−4。由于血细胞分析仪取液系统的材料为铝合金,其中同步带为聚氨酯材质,因此选择的加速率常数m=4。 测试使用应力STset根据同步带材料以及相关特性,同步带所能承受的最大应力,明确应力范围: 式中:V—同步带所受载荷时的速度;F—对同步带施加的应力;V0—同步带的初始速度;M—同步带自身重量以及所承受的重量;P—同步带承受的载荷;S—同步带的受力面积;Mbelt—同步带自身的重量;Mbearing—同步带所承受的重量。 式中:N—正压力;μ—摩擦系数,同步带材质为聚氨酯,因此摩擦系数0.5;f—摩擦力。 通过式(3)获得同步带所受载荷与速度的应力范围。通过计算得知X轴同步带工作时所允许的最大速度为0.06m/s,Y轴同步带工作时所允许的最大速度为0.11m/s,X轴同步带工作时所允许的最大正应力27.28N,由于是滑动摩擦,因此根据式(4)可知同步带带动同步轮的摩擦力为13.64N,Y轴同步带工作时所允许的最大正应力0.32N,即同步带带动同步轮的摩擦力为0.16N。根据血细胞分析仪取液系统的工作机制,X轴同步带运转速度最小0.05m/s,Y轴同步带运转速度最小0.09m/s,X轴同步带最小正应力21.28N,即同步带带动同步轮的摩擦力为10.64N,Y轴同步带最小正应力0.28N,即同步带带动同步轮的摩擦力为0.14N,因此,X轴同步带速度的加速因子AS1=2.07;Y轴同步带速度的加速因子AS2=2.21;X轴同步带摩擦力的加速因子AS3=2.61;Y轴同步带摩擦力的加速因子AS4=1.69。 综合加速因子计算根据式(5)得出: 式中:AS1—X轴同步带速度的加速因子;AS2—Y轴同步带速度的加速因子;AS3—X轴同步带摩擦力的加速因子;AS4—Y轴同步带摩擦力的加速因子。 所以,综合加速因子As−all=20.17。因此通过允许的最大应力,并在[Vmin,Vmax]与[Fmin,Fmax]中进行速度与所受载荷的正交试验,同时根据机械设计手册对同步带与同步轮的安装要求、转速要求、材料要求以及摩擦力极限要求,正交试验中在[Vmin,Vmax]与[Fmin,Fmax]中的数据变化精度要符合规定范围,速度在(0.005~0.01)m/s的范围内,摩擦力在(0.5~1)N之间变化。 81组正交试验数据,如表1所示。 表1 同步带的速度与所受载荷Tab.1 Speed and Load of Synchronous Belt 为验证同步带失效与速度和所受载荷之间的关系,选取第81组数据,当所有应力都处在最大时进行分析,通过图3和图4可知,X、Y轴同步带在启动时,参数瞬间发生跃升,Y轴同步带仅在启动瞬间,参数急剧爬升,之后趋于稳定并逐渐降低。 图3 X轴同步带主从动轮Fig.3 X−Axis Synchronous Belt Master and Slave Drive X轴同步带在启动后,速度、力、位移以及加速度在呈现短时间波动后,速度和位置持续爬升,加速度产生剧烈波动,受力情况持续上升,X轴的同步带失效的范围在(210~230)N,Y轴的同步带失效的范围在(280~300)N。 因此,通过图4和图5可以看出,全部参数达到加速极限后,当8.82s时,X轴加速度降低幅度过大,因此X轴发生失效的时间为8.82s时,此时应力为229.1N;当6.71s时,Y轴速度与加速度均降速幅度过大,因此Y轴发生失效的时间为6.71s 时,此时应力为295.8N,X轴失效速度为0.52m/s,Y轴失效速度为0.21m/s。 图4 Y轴同步带系统主从动轮Fig.4 Y−Axis Synchronous Belt System Master and Slave Drive 图5 X、Y轴同步带参数局部图Fig.5 Local Diagram of X and Y Axis Synchronous Belt Parameters 通过细胞分析仪取液系统的失效机理判定,不论X轴或者Y轴的同步带发生失效,都判定取液系统整体发生失效故障,X、Y轴同步带失效时间,如表2所示。 表2 X、Y轴同步带失效时间Tab.2 Failure Time of X and Y Axis Synchronous Belt 由于细胞分析仪取液系统是传输系统,因此,无论X轴还是Y轴的同步带,只要有一根损坏,整个系统都无法进行工作,因此从图6中可以看出,同组试验的前提下,Y轴的同步带失效时间比X轴同步带失效时间短,从整体数据来看,Y轴时间一直小于X轴时间,因此,将Y轴同步带的失效时间作为细胞分析仪取液系统的失效时间。 图6 X、Y轴失效时间Fig.6 Failure Time of X and Y Axes 通过表2获得取液系统机械传动结构中同步带的所受载荷和速度的极限状态函数: 式中:Tn—任何应力时的失效时间; α1—X轴速度的加速因子AS1=2.07; α2—Y轴速度的加速因子AS2=2.21; α3—X轴承受应力的加速因子AS3=2.61; α4—Y轴承受应力的加速因子AS4=1.69; ∂x—X轴失效节点处的应力值; ∂y—Y轴失效节点处的应力值。 对式(6)进行泰勒展开并通过最小二乘法获得矩阵常数项,最终得到极限状态函数(7): 改进型FORM算法在LD−FORM算法的基础上通过MC算法进行可靠度精度修正。利用LD−FORM 算法对失效数据的分析得到极限状态函数以及验算点,再通过Nataf变换原极限状态函数曲线以及Schmidt构造的正交阵进行旋转坐标轴,新的坐标轴指向验算点方向的方式,将原可靠度列式进行转换,通过MC算法以及牛顿迭代法求解非线性方程组的方式来计算失效概率,最终获得精度较高的可靠度。 为提高可靠度精度,将加速寿命试验得出的极限状态函数曲线通过Nataf分布方法对X空间进行变换到u空间,在u变量空间的极限状态函数曲线(x)=G[T−1(u)]=g(u)。 计算极限状态函数曲面g(u)=0上的最有可能失效点u(∗验算点)。由于抽样寻找验算点的方式过于抽象,如图7所示。 图7 抽样寻找验算点Fig.7 Sampling to Find Check Points 因此,通过响应面的方法,由失效面寻找最有可能失效点会更加直观。通过对比图8(a)的MC算法的失效面以及图8(b)改进型FORM算法的失效面,发现改进型FORM算法的失效面曲率大,MC算法的失效面曲率小。 通过图9的对比分析,最有可能失效点的收敛速度与失效曲面的曲率之间是相关的,如图8(a)可知失效面的曲率小,验算点定位有极大的误差,无法找到图9最后趋近的精准验算点,与之相反,如图8(b)所示,当曲率变大时,越容易寻到精确的验算点。因此改进型FORM算法通过响应面法来寻找验算点是可行的,通过减小寻找验算点的误差,进而求出的β值的精度更高。 图8 MC、改进型FORM算法失效面Fig.8 Failure Surface of MC and Improved FORM Algorithm 图9 改进FORM算法与MC算法趋近准确验算点的收敛速度Fig.9 Convergence Rate of the Improved FORM Algorithm and MC Algorithm Towards Accurate Verification Points 为了进一步提高验算点精度,将独立标准正态随机变量u的坐标系进行坐标变换,设新坐标系为u′,新坐标系的坐标轴为u′n指向验算点u∗方向。 满足这样条件的坐标变换矩阵为正交阵H,H的第n列为验算点方向的单位向量,如式(8)所示。 式中:||·||—向量求模。 H阵的构造可用Schmidt正交化方法实现,u’坐标系和u坐标系随机变量的相互关系为:u=Hu′,u′=HTu。相应的u′坐标系下极限状态函数g(u)变为:g(u)=g(Hu′) =g′(u′)。 在u′坐标系下极限状态函数g′(u′) =0曲面在新的平面上。将原可靠度列式变换成如下表达式: 式中:[·]—0~1函数,当自变量小于零时取1,自变量大于零时取0;∅n(·)—独立标准正态随机变量向量的联合概率密度函数为向量-u′的函数,使得 下列公式(10)视为一个条件失效概率计算表达式: 式(10)可采用Monte−Carlo法来求解,首先生产(n−1)维独立标准正态随机变量样本,设样本数目为N,则 式(11)中的统计量通过下列非线性方程来求解: 基于上述的加速寿命试验以及虚拟样机仿真技术,分别用改进型FORM算法、LD−FORM算法以及MC算法对81组失效数据进行算法优化。 三种算法对细胞分析仪取液系统机械传动结构随时间的变化所获得可靠度,如图10所示。 图10 三种算法可靠度对比Fig.10 Reliability Comparison of the Three Algorithms 如图所示,三种算法优化的数据结果都呈现出递减的现象,但LD−FORM算法处理的数据曲线波动较大,可靠度值从96.4%下降到91.0%,总体来看设备可靠度下降5.4%。 MC算法处理的数据曲线较LD−FORM 算法来看,波动变化较小,总体可靠度值整体有所提高,从97.5%下降到92.6%,下降范围4.9%。 改进型FORM算法较LD−FORM算法以及MC算法来看,可靠度值总体下降平滑,无较大波动,同时可靠度初始值高于其他两种算法,下降范围仅为2.9%,明显小于其他两种算法。 因此,基于上述分析,改进型FORM算法在优化数据方面明显优于其他两种算法,为可靠性评估提供了有效的设备基础数据。 通过文献[11]可知可靠性指标的计算误差以及计算改进型FORM算法中随机变量的灵敏度指标,判断影响因子,细胞分析仪取液系统机械传动结构随机变量灵敏度指标的重要度,如图11所示。X1=15%,X2=25%,X3=60%。 图11 随机变量灵敏度指标Fig.11 Sensitivity Index of Random Variable 通过表3以及图11分析可知,由相同样本数对加速寿命试验数据进行处理时,改进型FORM算法可靠度比LD−FORM算法精度高,可靠性指标计算误差小。 表3 三种算法评估分析Tab.3 Evaluation and Analysis of Three Algorithms 在样本数量远小于MC算法时,可靠度以及可靠度指标高于MC算法。通过文献[11]中灵敏度指标的计算,在加速寿命试验数据为基础的改进型FORM算法进行优化后,可以分析极限状态函数中随机变量的重要度,进而判断失效因子中哪个因子是最重要的。 通过计算结果可知,同步带所受载荷X3是最重要的失效因子。 因此,改进型FORM算法在可靠性评估上,减小可靠性指标计算误差,提高可靠度并提供失效因子重要度分析,使可靠性评估在有效节约时间以及经济成本的同时,其结果更加真实可信。 通过对全国医院的细胞分析仪取液系统的322组维修记录数据来看,根据观测值求取概率密度函数、分布函数、可靠度函数和故障率函数,通过计算获得平均无故障时间(MTBF),从而有效获得细胞分析仪取液系统试验台的可靠度值并与改进型FORM算法进行对比。 根据组距将322组数据分为20组,并对20组数据进行计算获得故障间隔时间的概率密度和故障间隔时间的经验分布函数三点图,如图12、图13所示。 图12 故障时间概率密度Fig.12 Failure Time Probability Density 通过图12和图13可以看出该血液细胞分析仪故障间隔时间可能服从威布尔分布或指数分布。 图13 故障时间经验分布Fig.13 Failure Time Experience Distribution 因此利用一元线性回归分析和最小二乘法,依据故障数据进行参数估计,并运用相关系数法来检验威布尔分布,可以确定该血液细胞分析仪故障间隔时间的分布规律。 根据计算获得线性回归方程: 对于威布尔分布的拟合效果,利用相关系数法对其进行检验,显著性水平α=0.10,经检验,细胞分析仪故障间隔时间服从威布尔分布。 进一步对细胞分析仪故障间隔时间分布函数进行D检验,显著性水平α=0.10,经检验,细胞分析仪故障间隔时间服从威布尔分布。 通过式(14)获得故障间隔时间的概率密度函数、式(15)获得分布函数、式(16)获得可靠度函数以及式(17)获得故障率函数。 该血液细胞分析仪故障间隔时间的概率密度函数、分布函数、可靠度函数和故障率函数分别,如图14~图17所示。 图14 概率密度函数 Fig.14 Probability Density Function 图15 分布函数Fig.15 Distribution Function 图16 可靠度函数 Fig.16 Reliability Function 图17 故障率函数Fig.17 Failure Rate Function 综合上述分析,全国医院的细胞分析仪取液系统的322组维修记录数据服从威布尔分布的同时,通过对概率密度函数、分布函数、可靠度函数和故障率函数的计算,经由MTBF计算获得细胞分析仪取液系统的可靠度值,计算公式,如式(18)所示。 式中:f(t)—故障间隔时间的概率密度函数。 针对全国医院的细胞分析仪取液系统的MTBF计算结果,如式(19)所示。 因此可靠度值为99.2%。 这里通过ADAMS 虚拟样机技术对细胞分析仪取液系统机械传动结构的速度与所受载荷的正交试验数据进行加速寿命试验仿真,获得细胞分析仪取液系统机械传动结构失效数据。 通过改进型FORM算法获得可靠度为98.7%,与维修数据计算MTBF获得的可靠度99.2%相比,改进型FORM算法在可靠性指标计算误差方面,误差小于LD−FORM算法和MC算法,所需样本数少,精度更高,更加贴近实际数据。 与此同时,改进型FORM算法可以针对灵敏度指标,通过获取的机械设备失效因子重要度,使可靠性评估更加完善。



2.2 仿真分析







3 改进型FORM算法评估
3.1 算法原理
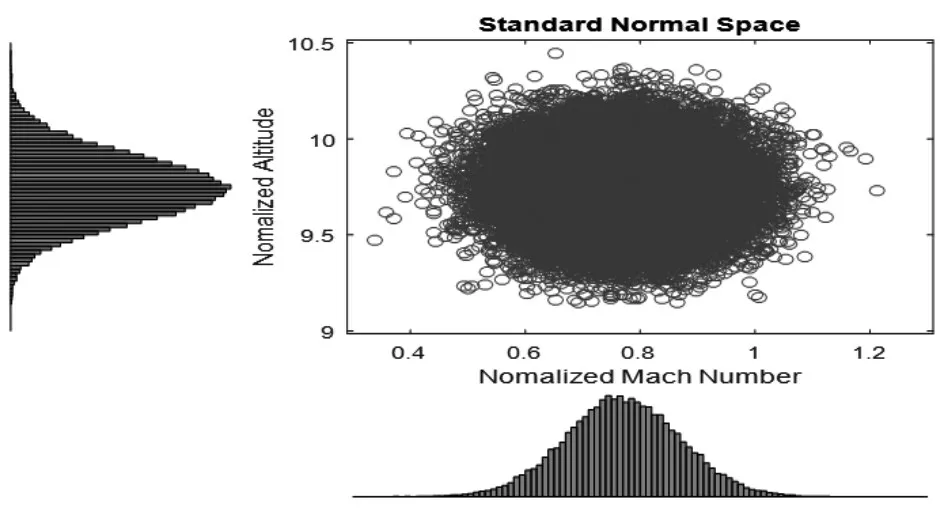







3.2 算例分析


4 数据验证对比









5 结论

