考虑初始残余应力的电梯导轨校直研究

毛慧俊，周自强

（1.常熟理工学院机械工程学院，江苏 常熟 215500；2.苏州大学机电工程学院，江苏 苏州 215000；3.江苏省机电产品循环利用技术重点建设实验室，江苏 常熟 215500）

1 引言

电梯导轨在使用时会由于过载、冲击等原因发生塑性变形，影响电梯运行的平稳性，此时就需要更换新导轨或对导轨进行再制造使其使其恢复使用前状态即可继续使用。目前主要针对加工过程的电梯导轨进行校直与残余应力研究，不考虑导轨的初始应力状态，文献[1−2]利用仿真数据建立神经网络模型，对校直行程进行预测，并对导轨多段校直进行了研究；文献[3]推导导轨校直后截面的残余应力分布公式；文献[4]利用ANSYS软件对电梯导轨辊式矫直后的残余应力进行了仿真研究。在导轨再制造的校直过程中，除了需要考虑初始挠度外，还需要考虑初始残余应力对校直过程的影响，目前也有一些针对初始残余应力情况下的校直研究，文献[5−7]对辊式矫直中理想弹塑性材料的二次反弯特性进行了研究，文献[8−9]推导了辊式矫直中二次弯曲的M−C特性，并研究了初次弯曲历史对二次弯曲的影响。但这些研究通常针对矩形截面进行理论推导，目前还没有针对T型导轨在考虑初始残余应力情况下的校直理论研究。

为研究初始残余应力对导轨校直的影响，并将其用于自动化校直设备的参数控制，以侧弯导轨的三点反弯校直为例，将其分为两个过程：弹塑性弯曲变形过程和反弯校直过程。侧弯变形过程基于三点弯曲理论模型，对导轨在使用过程中产生的塑性变形及残余应力进行分析，而反弯校直过程则是对具有初始残余应力的导轨校直进行弹塑性理论分析，确定初始残余应力对导轨校直的影响程度。

2 电梯导轨侧弯变形的残余应力计算

2.1 弹塑性力学分析的基本假设

电梯导轨的弯曲变形是一个弹塑性过程，符合弹塑性力学原理，在进行理论分析前做出以下假设：

（1）材料模型假设：导轨的材料模型为线性强化模型。

（2）单向应力假设：认为在弯曲变形过程中截面只受到弯曲正应力，而忽略其他应力的影响。

（3）无初始变形及残余应力假设：认为电梯导轨在使用前不存在初始残余应力，在使用过程中由于过载等情况造成导轨弯曲变形。

（4）不考虑包辛格效应的影响。

2.2 参数设定

电梯导轨一般由轨头、轨腰和底板三部分组成，其截面参数，如图1所示。

图1 电梯导轨截面参数及应力分布Fig.1 Sectional Parameters and Stress Distribution of Elevator Guide Rail

在进行弹塑性力学分析时，通常为了简化理论模型而采用无量纲参数。设定弹性极限弯矩为Me，弹性极限曲率为Ce，截面弹性区高度为He，截面所受弯矩为M，弯曲曲率为CM。定义量纲一化后的参数如下：塑弯比弯曲曲率比C=CM Ce=1ξ；相对高度z=2h H，h为纤维层距中性层的高度，取值范围为[−1，1]。

2.3 侧弯变形过程的加载和残余应力分布

由于导轨初始状态的残余应力为0，此过程为简单弹塑性弯曲过程。电梯导轨在侧弯过程中截面关于中性层对称，应力分布也关于中性层对称，由线性强化材料模型可知截面应力分布，如图1所示。

设材料的弹性模量为E，屈服强度为σs，强化系数为λ，则导轨弯曲变形的加载应力分布方程为：

式中：z—相对高度；C1—弯曲变形时的曲率比。

针对小变形导轨，塑性变形一般不会发生在导轨的轨腰和轨头位置，而只会发生在导轨的底板部位，根据文献[10]可知，导轨的加载弯矩表达式为：

侧弯变形过程的塑弯比为：

弯曲曲率比C1=1ξ1，则弯曲变形过程中的−C1关系为：

电梯导轨的回弹过程是一个弹性过程，相当于在截面上施加了一个−M1大小的弯矩。其卸载后的残余应力应视为加载应力σ1与回弹应力σr1的线性叠加，即：

回弹应力σr1是由−M1大小的弯矩形成的弹性应力，其分布函数为：

卸载后截面的残余应力分布函数为：

弯曲过程的加载应力分布和卸载后的残余应力分布，如图2所示。

图2 弯曲变形的截面加载应力和残余应力分布Fig.2 Loading Stress and Residual Stress Distribution in Section of Bending Deformation

2.4 侧弯变形过程挠度的数值求解

在三点反弯校直中，一般采用位移控制法控制校直压头的下压行程达到校直的目的，避免测量曲率带来的误差。若侧弯变形时弯曲曲率CM1=C1Ce，其中弹性极限曲率Ce为：

代入后得CM1为：

设导轨长度为L，弯曲变形时的挠度曲线为u（1x），（0 ≤x≤L），导轨回弹后的残余挠度曲线为uc（1x），截面x处的所受弯矩为M（1x），曲率比为C（1x），由弹塑性力学中的曲率微分方程可知，弹性段挠度曲线微分方程为：

塑性段挠度曲线微分方程为：

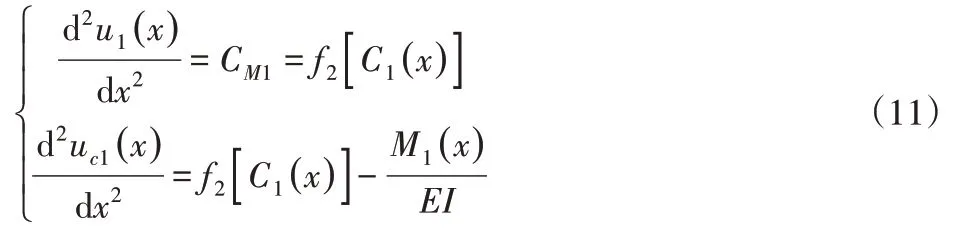
式中：u（1x）和uc（1x）—弯曲曲率比C（1x）的函数，一般通过直接积分法或数值法求解微分方程组，由于直接积分法计算困难，可通过数值差分法求解方程得到u（1x）和uc（1x），并计算u1（L/2）和uc（1L/2）得到加载挠度u1和残余挠度uc1。

3 考虑初始残余应力的反弯校直分析

在电梯导轨存在初始残余应力的情况下，截面的应力分布不再满足简单弹塑性弯曲过程的应力关系，属于复杂弹塑性弯曲过程。令反弯校直的初始挠度u0=uc1，初始残余应力σ0=σc1。

3.1 初始残余应力条件下的二次加载应力分布

设反弯校直时截面所受弯矩为M2，反弯曲率比为C2，则反弯校直时截面的加载应力分布为初始残余应力σ0与反弯校直的弯曲应力σM2的线性叠加。由于弯曲变形过程与反弯校直过程的加载方向相反，故：

反弯校直过程中的加载应力分布函数为：

（1）当ξ2≥ξ1时，为1类应力分布：

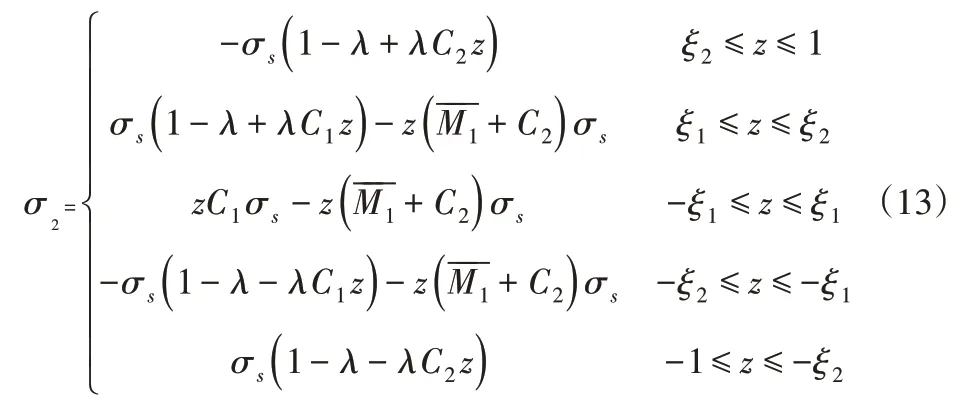
根据函数的连续性条件，求得ξ2为：

反弯校直的弯矩M2为：

由于不考虑包辛格效应的影响，反弯校直时弹性极限弯矩Me不变，此时截面的塑弯比=M2/Me。

（2）当ξ2<ξ1时，为2类应力分布：

根据函数的连续性条件，求得ξ2为：

此时反弯校直弯矩M2为：

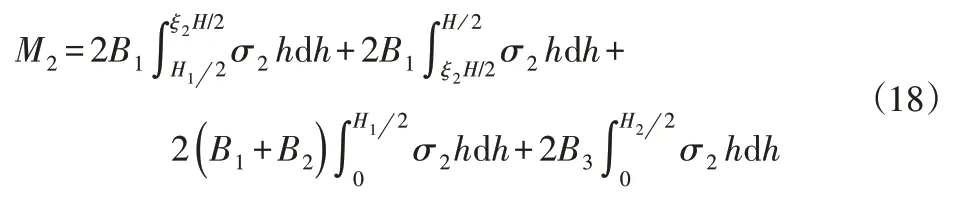
可以看到，不管反弯校直时截面应力分布σ2属于哪种情况，此时ξ2不再是简单弹塑性弯曲过程与C2成反比的关系，而是受到历史弯曲的影响，是C1和C2的函数，则弯矩比也是C1和C2的函数。

（3）应力分布边界

当ξ2=ξ1时，即为两种应力分布情况的边界条件。此时ξ2既满足情况1），又满足情况2），则：

求得C2与C1的关系为：

可以明显的看出，若截面要达到2类应力分布条件，反弯曲率比C2要大于弯曲变形曲率比C1。

3.2 初始残余应力条件下卸载后的残余应力分布

反弯校直卸载后的残余应力与侧弯变形时的残余应力相似，由于反弯校直卸载时回弹应力σr2方向与σ1相同，则截面的残余应力σc2为：

反弯校直过程截面的加载应力分布和残余应力分布，如图3所示。

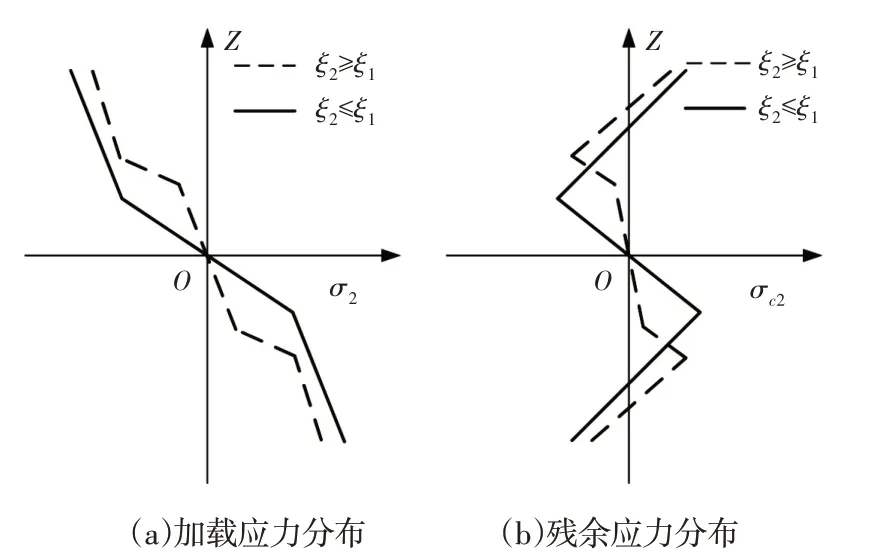
图3 反弯校直截面的加载应力和残余应力分布Fig.3 Loading Stress and Residual Stress Distribution in Section of Bending Straightening

3.3 反弯校直过程的M-C与u-C关系

为研究反弯校直过程的M−C关系与u−C曲线，首先需要确定C2与C1的关系，进而确定反弯校直的应力分布情况。若反弯曲率比C2=C1，则截面的弯曲曲率CM2=CM1，由此可得u2=u1，此时应力分布函数为1类应力分布，可以得出在[−ξ，ξ]区间内加载应力σ2<σ1，则反弯弯矩M2uc1。

若要达到校直目的，C2满足的条件为：uc2=u0，又因为u0=uc1，故uc2=uc1。因此，反弯校直需满足C2

设导轨反弯校直时加载挠度曲线为u（2x），卸载挠度曲线为uc（2x），u（2x）与uc（2x）建立的微分方程组也可通过数值差分法求解，进而得到反弯校直行程u2和残余挠度uc2。

4 基于有限元的算例对比与分析

以T75导轨为例，对上述理论残余应力分布、M−C模型和u−C数值求解模型进行分析，并通过有限元仿真验证理论模型。设导轨长L=500mm，截面参数为：B1=8，B2=24，B3=30，H=75，H1=8，H2=10，弹性模量E=205GPa，屈服强度σs=235MPa，线性强化系数λ=0.0173。

4.1 理论残余应力分布和有限元仿真模型的对比

设定弯曲曲率比C1=4.79，反弯曲率比C2=4.79，求得塑弯比：

在ABAQUS 仿真软件中建立导轨的三维模型，首先模拟导轨的弯曲变形过程：在导轨中点处加载u1后卸载；然后模拟反弯校直过程在导轨中点处反向加载u2后卸载，得到反弯校直的残余应力场。导轨中点处截面应力分布图，如图4所示。

将理论残余应力分布与有限元模型进行对比，如图5所示。

图5 有限元模型和理论模型的残余应力对比Fig.5 Residual Stress Comparison between Finite Element Model and Theoretical Model

可以看到，理论模型的侧弯最大残余应力约150Mpa，校直后最大残余应力约100MPa，与有限元模型结果基本一致。同时，可以看出在考虑初始残余应力的情况下校直后残余应力更小。

4.2 反弯校直过程的2 −C2与u-C曲线

图6 反弯校直的−C2曲线Fig.6 2 −C2 Curve of Reverse Bending Straightening

当C1=1时，弯曲变形过程未进入塑性，弯曲变形历史将不对反弯校直过程产生影响，此时的曲线一致。 当值和 应 力分 布 边 界对应 的C2值，如表1所示。

表1 侧弯变形的截面-C1值

表1 侧弯变形的截面-C1值

C1 M 1应力分布边界的C2 4.791.598.06 5.861.6310.19 7.291.6913.02 8.111.7114.65

反弯校直过程的uc2−C2曲线，如图7所示。其反映了截面的残余挠度和曲率比的关系。

图7 反弯校直的uc2−C2曲线

当C1=1时，uc2−C2曲线与uc1−C1曲线一致，当C1>1时，随着C1的增大，相同C2下对应的uc2更大，因此，应该减小反弯校直时的曲率比C2和校直行程u2。

在ABAQUS 中对导轨进行弯曲变形和反弯校直仿真，并计算u1、uc1、u2和uc2，将其与理论值进行对比，如表2所示。

表2 u1、uc1、u2、uc2的理论值和仿真值Tab.2 Theoretical and Simulated Values of u1，uc1，u2 and uc2

从表中可以看出，理论模型比仿真值略大，但在合理误差范围内。

4.3 反弯校直曲率比C2和校直行程u2的求解

由以上结论可知，若弯曲变形曲率比为C1，为满足校直要求，需满足uc2=uc1。由此求得C2−C1曲线，如图8所示。

图8 反弯校直的C2−C1曲线Fig.8 C2−C1 Curve of Reverse Bending Straightening

从图8中可以看出，若要达到校直目的，C2与C1基本成线性关系。

由于弯曲变形与反弯校直实际上是相反的过程，若初始弯曲挠度u0=uc1，在不考虑初始残余应力时校直行程u=u1，在考虑初始残余时校直行程u=u2，且满足uc2=uc1。理论校直行程u1、u2和仿真结果，如图9所示。可以看到，u2的理论和仿真值均比u1小0.1mm左右。

图9 反弯校直的u−u0曲线Fig.9 u−u0 Curve of Reverse Bending Straightening

5 结论

（1）若要达到校直目的，则曲率比C2