WPT、PCA与SVM结合的滚动轴承故障程度诊断

王帅星，黄 茜，王晓笋，巫世晶

（武汉大学动力与机械学院，湖北 武汉 430072）

1 引言

滚动轴承是旋转机械中的常用部件，同时也是易损坏部件。滚动轴承的主要元件之间多是点接触或线接触，容易在接触部位发生局部高压弹性变形。此外，工作过程中的高速转动、冲击等，极易引发轴承的疲劳破坏，也提高了轴承发生点蚀破坏的概率[1]。鉴于滚动轴承对于旋转机械正常运行的关键作用，对其进行状态监测与故障诊断具有重大意义。

目前，研究人员一般利用经验模态分解[2]（EMD）、小波变换[3]（WT）、奇异值分解[4]（SVD）、局部均值分解[5]（LMD）等信号处理方法，实现了滚动轴承故障位置的准确识别，但无法准确判定滚动轴承的故障程度。改进的多Q因子时频分析[6]、Volterra核函数[7]、多尺度熵[8]等方法虽然实现了滚动轴承故障程度的识别，但是却存在无法实现自动识别的缺点。为了实现滚动轴承故障程度的自动识别，这里提出了一种基于小波包变换（WPT）、主成分分析（PCA）与支持向量机（SVM）相结合的方法。首先，对采集到的滚动轴承原始振动信号进行小波包分解，然后对分解后的信号进行重构，并计算其能量作为故障特征。随后，对故障特征运用主成分分析进行降维处理，得到低维特征。把低维特征作为输入量对支持向量机进行训练与测试，从而实现滚动轴承故障程度的自动识别。最后，这里利用凯斯西储大学的滚动轴承数据对该方法的可行性和有效性进行了验证。

2 信号特征提取与故障诊断方法

2.1 小波包变换与信号重构

由于轴承振动信号是典型的非平稳信号，传统的信号分析方法如快速傅里叶变换（FFT）不易提取到相关故障特征。因而，时频分析方法如短时傅里叶变换（STFT）、小波变换（WT）、经验模态分解（EMD），在解决该类问题上得到了广泛的应用。

小波包分析是对小波分析改进后的一种时频分析方法，该方法能够对信号进行更加精细的时频分解。小波包分解对小波分解不再处理的高频部分进行了进一步的分解，从而显著提高了时频分辨率。因而，小波包分解可以应用于更加广泛的信号分析领域[9]。这里利用两层分解树简要描述了小波包的原理，如图1所示。其中，S代表原始信号，A代表低频，D代表高频，末尾的序号数表示小波分解的层数（也即尺度数）。

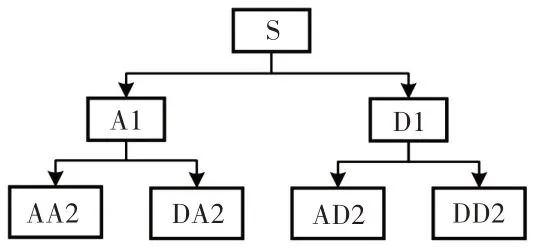
图1 两层小波包分解树Fig.1 Two−Layer Wavelet Packet Decomposition Tree

对原始信号进行n层小波分解后，需对分解后的信号进行重构。随后，根据式（1）计算重构后的小波的能量，式中m代表信号采样点数。

进行小波包n层分解后，可以得到2n个能量值。由于特征维度过大，存在信息冗余，因此这里利用主成分分析方法进行数据降维。

2.2 主成分分析

主成分分析是故障诊断中较为常见的数据降维方法。该方法的关键在于由多个特征中构造出少数几个综合特征。而这较少的综合特征可以综合反映数据信息，而且尽可能相互之间不存在重复信息[10]。

获取矩阵X主成分的步骤如下：

（1）求X的协方差阵V的特征根，记为：

（2）求λj对应的单位特征向量uj,j=1,2,…,k。

（3）取yj=u′j X即为X的第j个主成分，j=1,2,…,k。

（4）计算前m个主成分（m≤k）的累计贡献率，

在实际的特征降维应用中，通常会忽略掉贡献率相对较小的主成分，而累计贡献率的取值需要根据实际问题确定。选定相应的主成分作为故障特征后，将故障特征输入支持向量机，完成故障诊断模型的训练与测试。

2.3 支持向量机

支持向量机是由文献[11]于1990年在统计学习理论基础上提出的一种机器学习方法，该方法基于VC维理论和结构风险最小化原则，可以较好地解决小样本、非线性以及高维数等问题。经过二十多年的研究与改进，该算法得到了补充与优化。目前，该算法已经在模式识别、信号处理、故障诊断等领域得到了广泛的应用。

支持向量机的基本思想是将低维的非线性数据样本映射至高维线性空间，通过求解可以正确划分训练数据集并且具有最大几何间隔的分离超平面[12]，从而实现故障分类。

假设训练样本集为：

式中：xi∈Rn，yi={−1，+1}，i=1，2，…，N，xi—第i个实例，yi—xi的类标记；当yi=+1时，称xi为正例；当yi=−1时，称xi为负例，(xi，yi)称为样本点。

分离超平面H对应方程为：

式中：w、b—决定超平面的两个重要参数。如果所有样本点都要

能够正确地进行分类，则要满足约束条件：

而支持向量就是式（7）成立的样本点，即：

对于yi=+1的正例，支持向量落在超平面H1上：

对于yi=−1的正例，支持向量落在超平面H2上：

所以，支持向量的分离间隔为2 ‖w‖，2 ‖w‖最大等价于‖w‖22最小。因而，寻找最优分离超平面可以转化为求解约束凸优化问题。

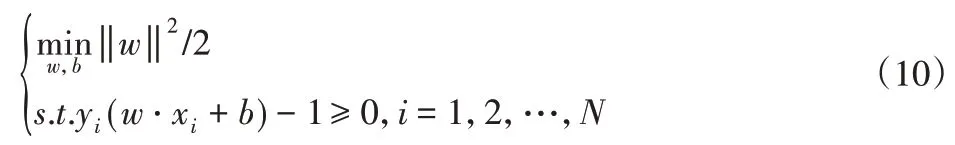
求解得到最优解w*、b*，进而可得到最优分离超平面。

因此，这里的故障识别流程，如图2所示。

图2 故障识别流程图Fig.2 Flowchart of Fault Identification

3 实验验证

3.1 实验装置

这里所使用的实验数据来自于美国某大学轴承数据中心网站[13]。该网站提供了滚动轴承正常状态与存在缺陷状态下的振动信号。凯斯西储大学的实验设备，如图3所示。

图3 凯斯西储大学轴承测试装置图Fig.3 Bearing Test Equipment of the Case Western Reserve University

在振动信号采集过程中，对不同的故障形式选取合理的传感器安装位置。安装位置包括驱动端（DE），风扇端（FE）和底板（BA）。这里针对6205−2RS JEM SKF轴承，基于美国凯斯西储大学的驱动端轴承故障数据，利用这里提出的诊断方法对轴承驱动端进行了故障诊断。

振动数据使用一个16通道的DAT记录仪采集，并在MATLAB中完成了数据的前处理。轴承的故障通过电火花加工进行预设。该网站提供的数据包含不同故障位置及损伤直径的振动信号。故障位置包含内圈、外圈、滚动体故障，损伤直径包括0.18mm、0.36mm、0.53mm，以上数据构成了这里验证方法的原始数据。

表1 驱动端轴承信息（单位：mm）Tab.1 Drive End Bearing Information（unit：mm）

3.2 不同故障位置的故障程度识别

这里选择负载为1hp 的原始振动数据，运用这里提出的方法，对三类故障位置的故障程度进行了识别，验证了这里提出的方法的可行性。从上到下依次为内圈正常以及三种故障程度（依次为0.18mm、0.36mm、0.53mm）的原始振动信号，如图4所示。

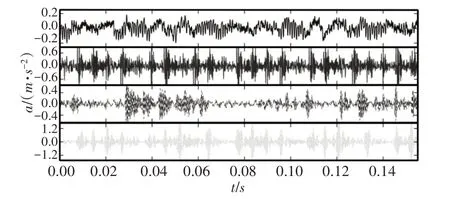
图4 内圈不同故障程度振动信号Fig.4 Vibration Signal of Different Fault Degree in the Inner Ring

仅从图4的时域信号，除了幅值以外，较难发现可以区别不同故障的有用信息。因而，对原始时域振动信号进行WPT变换，并计算重构信号能量，作为故障特征，进行故障诊断。对图4信号应用‘db4’母小波进行小波包3层变换，并进行重构信号能量计算后的能量分布，如图5所示。

由图5可知，不同故障状态的小波包变换后的能量分布差异较大。正常状态的能量主要分布在节点1、节点2、节点4；损伤直径为0.18mm的能量主要分布在节点2、节点3、节点7；损伤直径为0.36mm的能量主要分布在节点1，节点3，节点7；损伤直径为0.53mm 的能量主要分布在节点1，节点3，节点7。虽然，损伤直径0.36mm和0.53mm主要分布节点一致，但二者占比差别较大。因此，选取重构信号能量作为特征值是可行的。

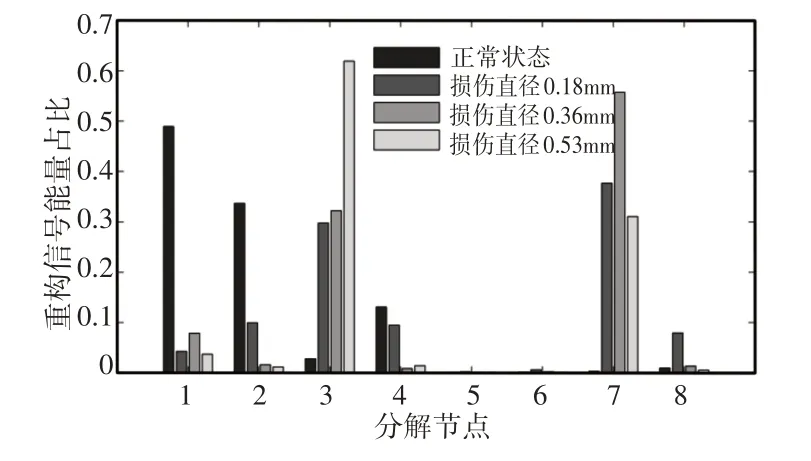
图5 重构信号能量分布图Fig.5 Energy Distribution of Reconstructed Signal

这里选取正常状态、损伤直径0.18mm、0.36mm和0.53mm原始振动数据共计360组数据，每种状态90组数据。其中，50组数据用于训练，40组数据用于测试。采用这里提出的方法对内圈、外圈、滚动体三种不同位置的三种不同故障程度数据进行处理。

在故障诊断过程中，主成分分析的累计贡献率、小波包分解层数和分解母小波类型均会对最终的故障诊断成功率产生影响。诊断成功率指的是正确分类个数与总测试数的比值。

首先，以‘db3’作为母小波类型对信号进行4层分解，研究主成分分析累计贡献率对轴承故障诊断成功率的影响，如图6所示。

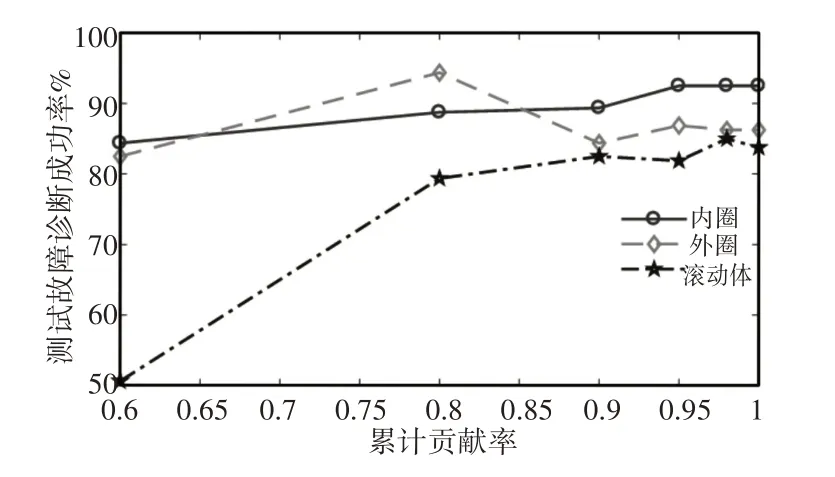
图6 不同累计贡献率的诊断成功率Fig.6 Effect of Cumulative Contribution Rates on Diagnostic Success Rate

成功率大致随着累计贡献率的升高而升高，当累计贡献率达到95%，可以达到一个较高的识别成功率。随着累计贡献率的增加，得到的原始信号的信息更丰富，诊断成功率也会随之增加。三个故障位置中，滚动体的故障诊断成功率对累计贡献率相对较为敏感。以‘db3’为母小波对原始信号进行分解重构，累计贡献率取95%，研究不同分解层数对故障诊断成功率的影响。不同分解层数对故障诊断成功率的影响，如图7所示。

由图7可知，当分解层数过小时，频率分辨率不高，故障诊断成功率较低，而当分解层数过大时，会导致故障特征维度过大，反而会降低故障诊断成功率。三个故障位置中，内圈与滚动体的故障诊断成功率对分解层数都较为敏感。

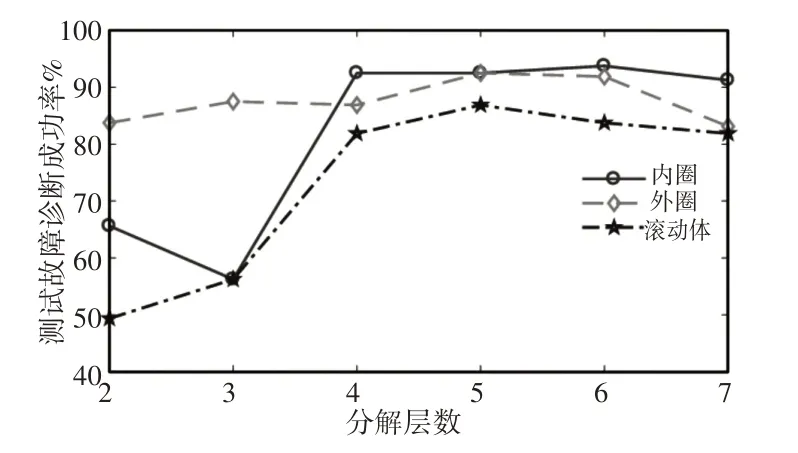
图7 不同分解层数的诊断成功率Fig.7 Diagnostic Success Rates of Different Decomposition Layers

另外，分解层数过大还会导致故障模型建立与诊断时间过长，分解层数与故障诊断时间之间的关系，如图8所示。

图8 不同分解层数的故障诊断时间Fig.8 Fault Diagnosis Time of Different Decomposition Layers

通过对比图8与图7，当分解层数为5时，既可以达到满意的故障诊断率，也并未过多影响计算效率。在选定分解层数为5，累计贡献率为95%的条件下，这里选择了7种母小波类型，分别为‘db3’‘、db4’‘、db5’‘、dmey’‘、sym5’、‘fk14’，探究了母小波类型与故障诊断成功率之间的关系。不同母小波类型的故障诊断成功率，如表2所示。

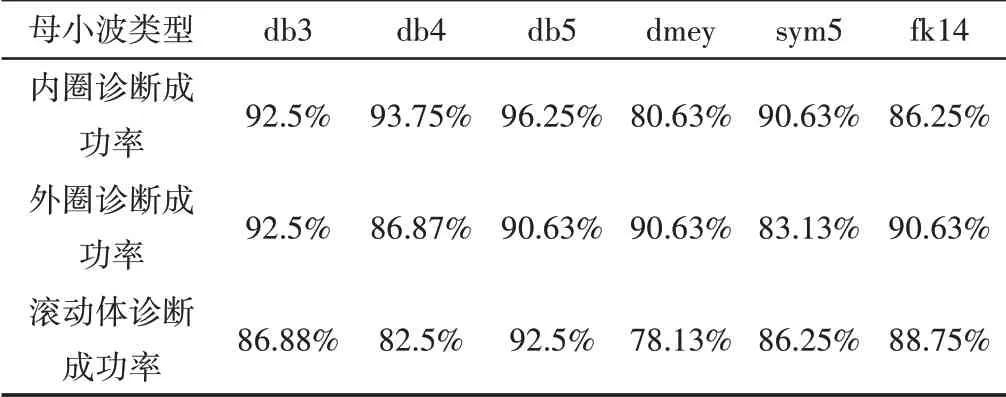
表2 不同母小波类型的故障诊断成功率Tab.2 Fault Diagnosis Success Rates of Different Mother Wavelet Types

由表2可知，不同的母小波类型会对故障诊断成功率产生较大的影响。在上述7种母小波类型中，适合于内圈、外圈、滚动体故障程度诊断的母小波类型分别为‘db5’‘、db3’和‘db5’，相应的最佳故障诊断成功率分别可达到96.25%，92.5%，92.5%。

综上所述，在进行故障诊断过程中，需要依据诊断位置选取合适的累计贡献率、分解层数和母小波类型，才能保证较高的诊断成功率和诊断效率。对内圈进行故障诊断的最佳参数为累计贡献率95%、分解层数5层、母小波类型‘db5’；对外圈进行故障诊断的最佳参数为累计贡献率95%、分解层数5层、母小波类型‘db3’；进行故障诊断的最佳参数为累计贡献率95%、分解层数5层、母小波类型‘db5’。针对上述三种参数配置，利用这里的诊断算法进行故障诊断，诊断结果，如图9所示。

在图9中，共计160组测试样本，从左至右分为四个部分，依次是正常状态、损伤直径0.18mm、0.36mm、0.53mm的测试样本。如果预测标签与实际标签一致，则说明该样本诊断成功，否则为误诊，预测标签所在的位置代表其误诊为的故障类型。

图9 不同故障位置故障程度诊断效果图Fig.9 Diagnostic Results at Different Locations

对比图9的三幅图发现，故障诊断方法对于三类故障位置的正常状态均能够进行正确识别；内圈故障程度诊断主要是将损伤直径0.53mm误诊为0.36mm，外圈故障程度诊断主要是将损伤直径0.18mm误诊为0.36mm和0.53mm，滚动体故障程度诊断主要是将损伤直径0.18mm误诊为0.36mm和0.53mm以及将损伤直径0.36mm误诊为0.18mm和0.53mm。

4 结论

针对滚动轴承故障程度诊断成功率低且难以实现自动识别的问题，这里提出了一种针对滚动轴承故障程度的诊断方法，并应用凯斯西储大学的试验数据对该方法诊断成功率进行了验证，得到了如下结论：

（1）不同故障位置对于参数的敏感性不同，内圈故障对于分解层数最为敏感，外圈对于三个参数敏感性差别不大，而滚动体对于累计贡献率和分解层数都较为敏感。

（2）不同故障位置的最佳诊断成功率不同，内圈的最佳故障诊断成功率最高为96.25%，外圈与滚动体均为92.5%。

（3）从实验结果来看，这里提出的基于WPT、PCA与SVM的故障诊断方法可以有效地对滚动轴承不同故障位置的故障程度进行识别。