An air-rail inter-modal strategy for aircraft recovery

Hong LIU, Fng SUN, Yu ZHANG

a Department of Air Traffic Management, Civil Aviation University of China, Tianjin 300300, China

b Department of Science, Civil Aviation University of China, Tianjin 300300, China

c Department of Civil and Environmental Engineering, University of South Florida, Durham FL 33620, USA

KEYWORDS Aircraft recovery;Airline operations modelling;Airline scheduling;Air-rail inter-modal network;Network modelling

Abstract It is common that airlines encounter a disruption of a flight schedule, which is mainly caused by resource shortages. In case of a disruption, subject to scarce resources, most of airlines lose flexibility of performing aircraft recovery on the basis of business interest priorities and need to delay, swap, and cancel flights. This paper proposes an air-rail inter-modal strategy to incorporate a High-Speed Rail (HSR) transport mode into an aviation network for aircraft recovery. The air-rail inter-modal strategy focuses on occasionally operational integration of existing airside and HSR infrastructure capacities. It is different from air-rail cooperation implemented in Europe which emphasizes a long-term strategy. In addition to modelling the air-rail inter-modal strategy,an inter-modal time-band network is presented. Modelling is applied to a pure aviation network and the inter-modal network. Comparison results show that the inter-modal air-rail strategy helps to reduce the number of cancelled flights and the total disruption cost.

1. Introduction

Most flight delays and cancelations can be due to two major resource shortages: airline resource shortages and airport and airspace capacity shortages.Aircraft taken out of service due to unforeseen mechanical problems, earlier upstream disruption, no enough time for a minimum turnaround time,and absent crew can lead to airline resource shortages.Airport and airspace capacity shortages mean that the number of departures and arrivals exceeds the air field capacity of an airport, resulting from inclement weather reducing airport throughput to air traffic control.

The reason for a disruption can be analyzed in detail, but for airlines, it is more important to minimize negative consequences emanating from the disruption and get a feasible,cost-minimizing plan to recover from the disruption.Most airlines have developed Airline Control Centre (ACC) or Airline Operation Centre(AOC)to manage the resources for recovering from disruptions. Aircraft, crews, and passengers are the most important and manageable resources.When schedule disruptions occur, an ACC monitors and manages these relative resources to recover from the disruptions. Aircraft recovery has a great influence on airlines’ revenue and is the first and most important step.For aircraft recovery,airlines face a myriad of options to utilize scarce aircraft more efficiently,including delaying flights, cancelling flights, and rerouting affected aircraft under some constraints on aircraft balance requirements, maintenance requirements, and curfew restrictions. As the resource of available aircraft is always scarce and valuable during a disruption,it is a great challenge for an ACC to solve the problem of aircraft recovery from a business perspective when a disruption occurs.

Transportation modes are coupled and interdependent.Competition between air service and High-Speed Rail (HSR)has attracted much attention,but in some cases,HSR may also have an intermodal complementary role to air transportation.Intermodal transportation is one of the desired recovery solutions for airline disruption management. Evidence has shown that HSR can provide feeding services to long-haul air services in hub airports, particularly those with HRS stations.Meanwhile, the project of HSR has grown greatly in China and established a specialized network of railways with speeds of 250-350 km/h, which is the world’s longest HSR network and also the most extensively used one. By the end of 2018,HSR has extended to 30 of the country’s 33 provincial-level administrative divisions and almost reached 29,000 km in total length, accounting for about two-thirds of the world’s HSR tracks in commercial service.Furthermore, the project boom continues, and the total HSR length will reach 38000 km in 2025.

Therefore, HSR is a suitable replacement for short-haul flights from the speed to the facility especially when the resource of available aircraft is in shortage. It is suggested in this paper that an ACC could cooperate with HSR to recover flight schedule when a disruption occurs. The strategy offers more flexibility for an ACC to reschedule affected flights with business interest priority and provide reliable service to passengers.

HSR belongs to public transport whose departure time is scheduled and cannot be influenced by airlines. Only the excessive capacity of services can be utilized by airlines.The characteristic of public transport may bring some convenience from the perceptive of cost of renting HSR, for example, the cost of utilizing HSR is only related with the number of occupied seats, which provides airlines with a more flexible scheme to utilize HSR. Trains with sufficient capacity of services can be utilized as substitutions for flights whose departure (a station for flight refers to an airport that an airline servesand arrival stations will be passed by trains in a proper order.

This paper studies the aircraft recovery problem when a disruption is caused by resource shortages. With the cooperation of HSR, an air-rail inter-modal recovery strategy is proposed and modeled. The remainder is organized as follows: in Section 2, relevant literature is summarized. In Section 3, the aircraft recovery problem is presented,and an air-rail inter-modal strategy is proposed. In Section 4, a mixed integer linear programming model is developed,and the method of constructing an air-rail recovery network is given. In Section 5, the proposed research method is validated with numerical examples.Conclusions are drawn and described in Section 6.

2. Literature review

Disruption is defined as an act of delaying or interrupting a continuity. It can be divided into two categories: aircraft disruption and station disruption.An aircraft disruption arises when a plane is not available and at least one of its assigned flight legs is prevented from flying.When weather and congestion reduce the capacity of a station and the schedule of flights departing from or arriving at the station is disrupted, it is referred to as station disruption.

Recovery of an aircraft disruption problem always deals with the recovery of a flight network and considers the impact of operation on downstream flights.Recovery of a station disruption considers only those directly affected flights which depart from and arrive at the disrupted station. The solution of a station disruption may give rise to an aircraft disruption.For example, a flight is suggested to be cancelled during the recovery of a station disruption, and the route of the aircraft which executes the cancelled flight is disrupted; therefore, a station disruption is followed by an aircraft disruption. The results of an aircraft disruption can be an input to the recovery of a station recovery, which helps airlines accurately estimate the cost of cancelling a flight considering the impact downstream. Therefore, this paper focuses on the problem of aircraft disruptions.

When an aircraft disruption occurs, aircraft recovery is firstly solved,which is to reassign the route of the affected aircraft to recover from the disruption. The aircraft recovery problem was firstly proposed by Teodorovic´ and Guberinic´,who focused on recovering a schedule with the objective of minimizing the delay cost by swapping and delaying flights when one or more aircraft are out of service. Rerouting options were firstly expanded and combined with flight delays,cancellation, and ferrying in a model proposed by Yan and Yang.More detailed description and models can be found in Refs.10-14.It is worth mentioning that Rosenberger et al.presented an aircraft selection heuristic for the aircraft recovery problem, which helps an ACC select a subset of aircraft which are rerouted for optimization prior to rerouting aircraft.

A limitation in most of the existing models for aircraft disruptions is that most of the literature considered only rescheduling their flights to recover from a disruption, not incorporating alternative transportation modes. Zhang and Hansenproposed a model to recover from a station disruption focusing on recovering the schedule of flights departing from or arriving at a station whose capacity is short-fall or closed, in which it is suggested that airlines could incorporate ground transport modes into their operations when there is a significant capacity shortfall. Recently, more and more people have paid attention to researching multimodal transportation networks. These studies include substitution of air passenger transport by HSR for mitigating airport congestion,collaborative decision-making at the airport level when a disruption occurs, and using ground transportation for aviation system disruption alleviation.Sun et al.proposed the need for construction of an open-source dataset for large-scale multimodal transport systems and comprehensive assessment of new emerging transport modes. Wang et al.studied the robustness of the airports network in the face of an unexpected disturbance.

However, to our knowledge, little has been studied for multi-modal recovery of aircraft disruptions. In this paper, a mixed integer linear mathematical model is developed to minimize the total cost including delay cost,cancellation cost,and substitution cost and to generate recovery plans which help airlines make decision on flight departure times, flight cancellations, flight substitutions, and assigning aircraft to flights.This model is based on an inter-modal time-band network generating a set of candidate flight legs for each flight.

3. Problem presentation

The problem discussed in this paper is how to make aircraft recovery in case of a disruption preventing an aircraft from flying at least one of its assigned flights. In a traditional airline recovery operation,an ACC needs to reassign other candidate aircraft to recover from the disruption. Consequently, these candidate aircraft’s original routes are disrupted indirectly.In order to reduce adverse effects, the ACC adjusts the flight schedule and aircraft routes by means of retiming the departures of flights, cancelling flights, and revising the routes of affected aircraft in order to return back to the initial schedule with a feasible and cost-minimizing plan.

To help an ACC flexibly recover a flight with business interest priority and offer better and reliable service for passengers,this paper incorporates the HSR mode into an air traffic network.A line of HSR train Gi can be represented by its private HSR train type G along with a train number i. It is common that a line of HSR Gi passes many intermediate stations. If HSR Gi travels from station sto station s,then we call it pass

For example, a sample flight schedule presented in Table 1 assigns 5 aircraft to service 14 flights over 4 stations. The scheduled routes for aircraft 1, 2, 4 and 5 all originate from Beijing Capital International Airport (PEK), but terminate at Shanghai Hongqiao International Airport (SHA), PEK,Changchun Longjia International Airport(CGQ)and Zhengzhou Xinzheng International (CGO), respectively. Aircraft 3 originates from SHA, but terminate at PEK. Suppose that a disruption occurs at 12:00 so that aircraft 3 is not able to execute its flight plan, and the recovery horizon T = [12:00,24:00], A= ｛3 ｝, A= ｛1，2，4，5｝.

Table 2 presents a sample schedule of the HSR train G9 from Beijing South station to Shanghai Hongqiao station.There are 3 intermediate stations,namely Tianjin South,Jinan

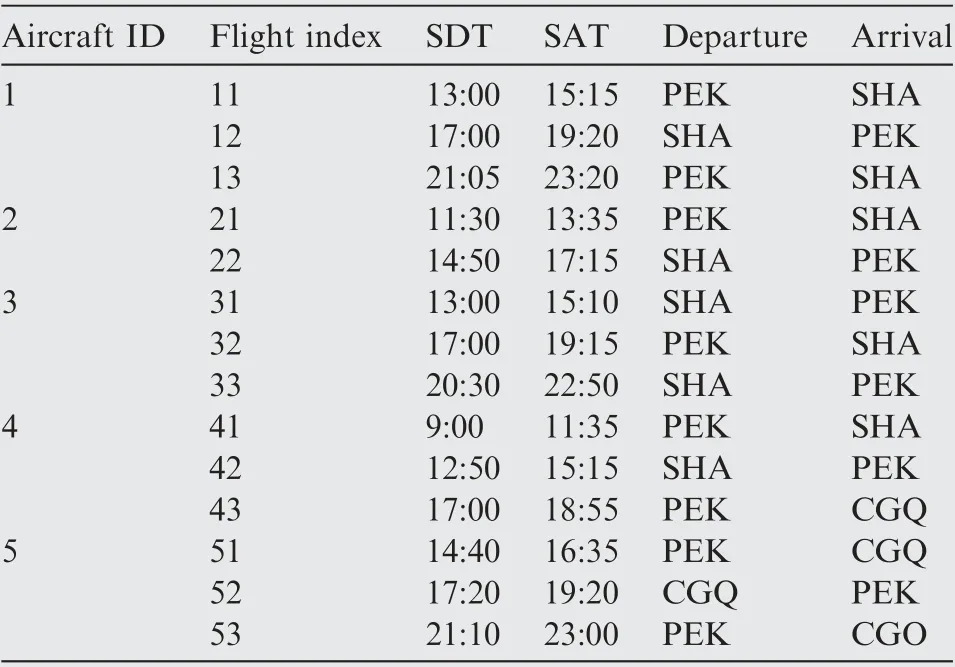
Table 1 Sample flight schedule.

Table 2 Sample HSR train schedule.

4. Model formulation

In this section, some basic assumptions will be given, and an air-rail recovery model relating to the problem described above will be established.

4.1. Basic assumptions

Before stating the air-rail recovery mathematical model, the following four assumptions are made, namely single fleet, no ferrying,no maintenance requirements,and fixed transfer time between an airport and a railway station.

(1) It is assumed that the aircraft are of the same type. As aircraft of different types have different characteristics such as passenger capacities, ranges, and requests for pilots and crew, rerouting aircraft from different fleets will complicate the recovery problem, and airlines typically avoid reassigning fleets during operational disruptions in reality.

(2) No ferrying aircraft (transporting empty aircraft to another location)is permitted.It is known that aviation fuel is costly,and assigning a departure slot temporarily is troublesome for airlines. Moreover, a temporal flight plan should be submitted. Waiting for an approval by the authority is time-consuming. Thus, a ferrying aircraft is the last choice and is avoided at all possible.

(3) To simplify the model, maintenance requirements and crew constraints are not considered;however,the model can be easily expanded incorporating these requirements.

(4) The transfer time of passengers from an airport to a railway station is different from one city to another, and it is also affected by the congestion state of the road traffic when a disruption occurs. For simplicity, the transfer time is set to be a fixed buffer time.

4.2. Model formulation

The approach of generating flight directional copies to represent flight legs has been employed in various recovery models.Eq. (3) shows the cost of making flight substitutions by HSR.The first term in Eq.(3)is the delay cost caused by flight substitution. Since the duration of HSR is usually longer than the duration of a flight, a coefficient α is multiplied to adjust the balance between the duration of HSR and the duration of the flight. The cost for each substitution of one flight by an HSR train is calculated by multiplying the cost of delaying one flight per minute by the delay time and the coefficient α which is a factor to evaluate the impact of the difference between HSR and air travel time. The second term in Eq. (2)is the cost that the airline pays to the ground transportation service providers for transiting passengers. The largest part of the cost is paid for train tickets. The airline may need to cooperate with a public urban transport service provider(i.e., a public bus company) to transfer passengers from airports to railway stations. Note that airlines are resistant to pay for transfer fees and would negotiate with ground transportation service providers to reduce these expenditures. A resistance factor dis introduced and multiplied with the corresponding cost of train tickets.The larger the factor is,the more resistant airlines are to pay for transiting passengers.

Table 3 Notations of parameters and variables.

5. Model prerequisites

To generate the copies of the flight,the problem is transformed into an inter-modal time-band network. The process of constructing such a network is the process of generating the copies of flights which include the copies executed by aircraft and the pseudo flight copies substituted by HSR.The copies in the network capture the delay of the corresponding copy for each flight.An inter-modal time-band network is established by inserting the above pseudo flight copies into the air traffic time-band network. The recovery scheme is illustrated in Fig. 1.

Algorithm 1. Pseudo flight copies generation algorithm.Input:Affected flight set F A0，A1，H（）, database of the HSR train DBHSR, buffer time tbuff for transferring passenger from an airport to a railway station Output: GF，G，FG Step 1. (Pre-process to generate the available HSR interval set G’)Sort the set F A0，A1，H（） with a keyword of SDT and a sub keyword of SAT to generate a set of pairs of stations■■■■S=∪f sdp f ，sarf .■■∈S, search DBHSR, and put Gi into G’ if Gi passes through sj，sk For sj，sk ■■.Step 2. For f ∈F,put f into the set FGi sdp ■■if there exists a line of HSR Gi ∈G， satisfying the following constraints:f ，sarf■■(1) Gi passes through the interval sdp f ，sarf ,(2) tsdp Gi ≥t+tbuff, where tsdp f f Gi is the passing time of Gi from station sdpf and t is the scheduled departing time of f.Create a pseudo flight copy with two-dimensional weight NGi sdp■■，Df ■■into the set Gf and G where NGi sdp f ，sarf■■Gi sdp f ，sarf and put Gi sdp f ，sarf■■is the available capacity of the HSR train and Df f ，sarf■■=tsar Gi-tarf -tm is the delay time in the time-band network calculated by subtracting f Gi sdp f ，sarf the scheduled arrival time of flight tar f and the average passengers transition time tm from the arrival time of the HSR train.

To illustrate the generation of pseudo flight arcs,the sample scheduled flight presented in Table 1 will be used.Fig.2 depicts the available HSR schedule in a railway time-station network.The network consists of 22 high-speed railways over 3 stations,namely Beijing,Changchun,and Shanghai.Station Zhengzhou and HSR trains to Zhengzhou are not contained in the network. The reason is that the only flight to Zhengzhou is operated by aircraft 3 from Beijing at 21:00, but there is no HSR line starting later than 21:00 from Beijing to Zhengzhou.

Set the buffer time from PEK to Beijing South Railway Station to be one hour.For flight 11,we can query the HSR timetable and find that there are 3 lines of HSR passing through(PEK, SHA) with scheduled departure time from PEK later than 14:00, so these HSR lines are put into G11 and G. Similarly, pseudo flight arcs can be obtained for other flights.

For the given scheduled flight presented in Table 1 and the HSR data in Fig.2,the generated air-rail time-band network is illustrated in Fig. 3. The flight arcs are marked by black lines.The pseudo flight arcs obtained by the pre-process step in the pseudo flight copies generation algorithm are marked by cyan lines.This network contains 45 flight arcs and 35 pseudo flight arcs.

6. Computational results

The data used to evaluate the effectiveness of the air-rail intermodal mathematical model for recovery includes two parts,namely flight and railway schedules. In this paper, the flight schedule is from flight plans of a big airline in China, while the railway schedule is from the China High-Speed Railway Network (CHSRN). A flight recovery network is generated based on the flight and railway schedules.This generation process is coded on MATLAB. All computations are performed on a Think Station with CPU i5-7200U and 8 gigabits of RAM. The integer programs are solved with IBM CPLEX.

6.1. 5-aircraft sample computational results

There are two types of HSR in operation,namely normal highspeed railway (G) and China high-speed railway (D). The prices and average durations of the two types are different from each other. Relating to the above HSR network, the prices and average durations between Beijing and Shanghai and between Beijing and Changchun are as listed in Table 4.

Before presenting the full set of computational results, the values of the parameters used in the recovery model are given.The cost of delaying one flight is 22.48 RMB per minute,which is calculated from the fiscal year cost of the airline operation 98 415 million RMB divided by the yearly flight hour 1216013.The number of passengers on each flight is 142, which is obtained from the average capacity of medium aircraft 180 multiplied by the occupancy rate 79%. The cancellation cost is 674.22 RMB per passenger, calculated from multiplying the cancellation cost per passenger $102.31 by 6.59, which is the average yuan’s exchange rate against the US dollar from year 2015 to year 2019. Since Hu’spaper did not consider air-rail model recovery, some additional assumptions are necessary. In particular, we assume that the transiting cost for each passenger is based on 1.4 RMB per minute and is determined by multiplying this value by the difference between the actual arrival time of the reassigned flight or HSR and the scheduled arrival time of the cancelled flight.

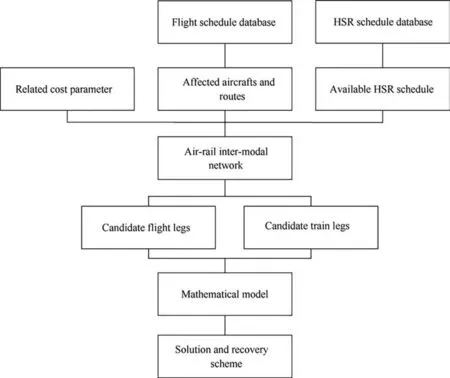
Fig. 1 Air-rail inter-modal recovery scheme.

For the 5-aircraft sample mentioned previously,5 scenarios are considered.In each scenario,one aircraft is grounded.The objective again is to minimize the total cost resulting from flight delays,passenger reassignments,and flight cancellations.The output of the optimization solver is used to generate new aircraft routes and passenger transiting itineraries between different flights and HSR, and cancelled flights.

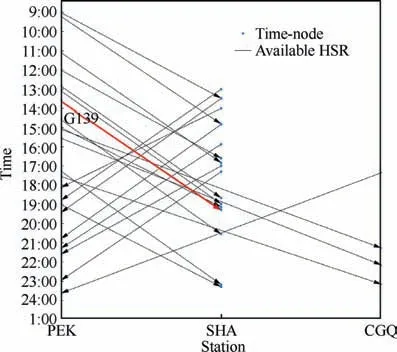
Fig. 2 Time schedule and available HSR train schedule.

Table 5 shows the results of the 5 scenarios. The table is divided into five sections (recovery mode, total cost, substituted flight ID set, cancelled flight ID set, and total delay time). For each scenario, air-rail inter-modal recovery is compared with air-only modal recovery. In scenarios 1 and 5, the optimal solution of air-rail inter-modal recovery is the same as that of air-only modal recovery. In scenario 4, the substituted flight{43}which is cancelled under air-only modal recovery reduces the total recovery cost. In scenarios 2 and 3, the cancelled flight ID set is different from the substituted flight ID set, and the optimal solution under air-rail inter-modal recovery is lower compared with that under air-only modal recovery.

6.2. Larger-scale sample computational results

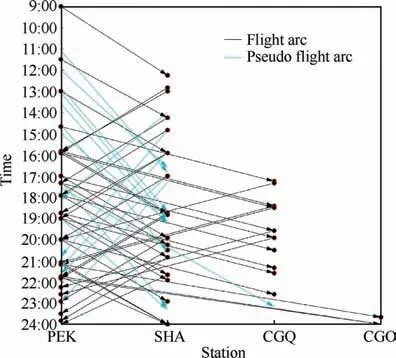
Fig. 3 Air-rail time-band network.

Table 4 HSR prices and average durations.

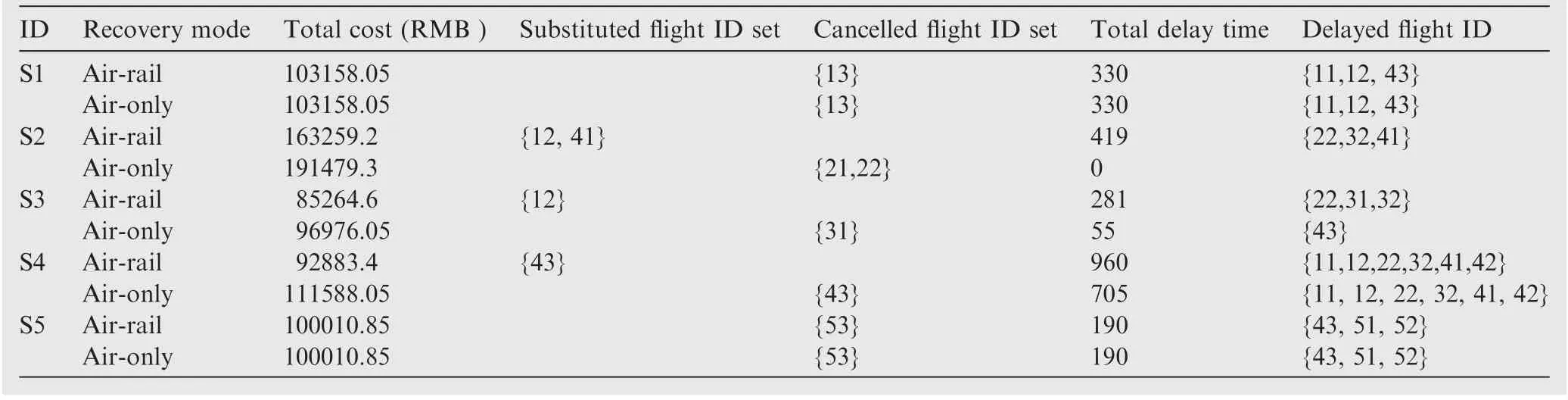
Table 5 Solution for the sample problem.

For larger-case computational experiments, the data required for the recovery model include flight information (flight ID,flight departure and arrival times, and departure and arrival airport stations) and aircraft information(aircraft ID and aircraft capacities). These data along with the original schedule for one day are obtained from the airline, while passenger information (number of passengers on each flight and cancellation cost for each passenger) are hypothesized for testing purposes. The flight data set includes 118 aircraft, and the number of flight schedule is 295 over 71 stations. The airline network includes 269 pairs of cities and the HSR data set includes 226 HSR lines covering 11 stations.

Fig. 4 Comparison of total cost between air-rail and air-only modals.

Table 6 Cost comparison between air-rail and air-only modals.

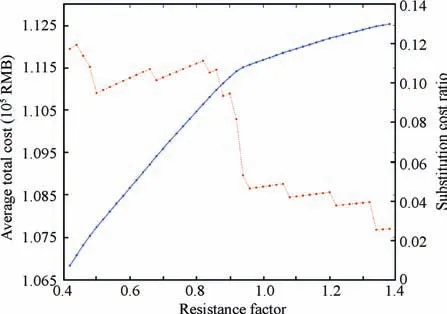
Fig. 5 Resistance factor sensitivity analysis.

For the 118-aircraft sample, computation experiments run 118 times for each of the two methods. One different aircraft from each other is grounded each time. Test results show that the optimal solution of air-rail inter-modal recovery is 18 times lower than that of air-only modal recovery. The average total cost reduction is 17.65%.Compared with other cases,18 cases show that airline routes are more robust under air-rail intermodal recovery methods. Fig. 4 displays the total costs of the two methods for each of the 18 tests. From the figure,the maximum cost reduction is 54,000 RMB of air-rail intermodal transportation compared to that of air-only modal.

Table 6 gives a comparison of the average results obtained from the solutions of 118 times tests of the two methods.Compared air-rail modal with air-only modal,the average total cost reduction is 3.57%,the average flight cost increment is 2.22%,and the average cancellation cost reduction is 14.07%.Parameters affecting the results include the airline and HSR network structures, the percentage of China high-speed railway in the HSR network,and resistance of the airline paying for substitutions of disrupted flights by HSR. Since the network and the HSR type are relatively stable,we focus on the impact of resistance of the airline paying for substitutions of disrupted flights by HSR.

Fig. 5 shows two curves. The resistance factor is set to be from 0.4 to 1.4 with an increment step of 0.02.The horizontal axis is the resistance factor, the vertical axis on the left is the total cost, including flight delay cost, substitution cost, and cancellation cost, and the vertical axis on the right represents the percentage of the substitution cost in the total cost.

The trend of the red curve shows that the lower the resistance factor is, the lower the average total cost is. There is one turning point when the resistance factor takes a value of 0.92. The slope of the line segment when the resistance factor lies between (0.92, 1.4) is smaller than that of the other segment when the resistance factor lies between (0.4, 0.92). The blue curve shows that the changing trend of the substitution cost percentage when the resistance factor increases from 0.4 to 1.4. The results in Fig. 5 indicate that higher resistance factors leave lower possibility for flight substitutions and passenger reassignments, which leads to more canceled flights. To reduce the total cost, airlines can differentiate disrupted passengers based on the resistance factor and adopt different tactics of reassignments.

7. Conclusions

(1) An air-rail inter-modal strategy is proposed to incorpo

rate an HSR transport mode into an aviation network for aircraft recovery during airline schedule disruptions.A solution scheme based on modification of a time-band network and generation of candidate pseudo flight legs is developed in this paper. A mixed integer linear programming mathematical model is constructed to verify the air-rail inter-modal strategy.

(2) The mixed integer linear mathematical model is developed to minimize the total cost including delay cost,cancellation cost, and substitution cost and to generate recovery plans which help airlines make decision on flight departure times, flight cancellations, flight substitutions by HSR trains, and assigning aircraft to flights.

(3) Numerical experiments are performed to demonstrate the proposed modelling and solution algorithm, solving air-rail inter-modal recovery. Experimental computations are performed with flight schedule operation data from one of Chinese airlines and railway resource data from China high-speed railway network. By comparing recovery outcomes for a pure aviation network and an air-rail intermodal network, it shows that the air-rail inter-modal strategy helps to reduce the number of cancelled flights and the total disruption cost.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This study was co-supported by the Tianjin Natural Science Foundation,China(No.18JCQNJC04300),the National Natural Science Foundation of China (No. 71801215) and the Foundation for University Key Teacher by the Ministry of Education of China (Nos. 3122018C033, 3122015L010).