Direct thrust control for multivariable turbofan engine based on affine linear parameter-varying approach

Yiyang ZHU, Jinquan HUANG, Muxuan PAN, Wenxiang ZHOU

Jiangsu Province Key Laboratory of Aerospace Power System, College of Energy and Power Engineering,Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

KEYWORDS Turbofan engine;Direct thrust control;Linear Parameter Varying(LPV) approach;Particle Swarm Optimization(PSO);Robust LPV H∞filter

Abstract A novel turbofan Direct Thrust Control(DTC)architecture based on Linear Parameter-Varying (LPV) approach for a two-spool turbofan engine thrust control is proposed in this paper.Instead of transforming thrust command to shaft speed command and pressure ratio command,the thrust will be directly controlled by an optimal controller with two control variables.LPV model of the engine is established for the designing of thrust estimator and controller.A robust LPV H∞filter is introduced to estimate the unmeasurable thrust according to measurable engine states. The thrust estimation error system is proved to be Affinely Quadratically Stable (AQS) in the whole parameter box with a prescribed H∞performance index γ.Due to the existence of overdetermined equations, the solving of controller parameters is a multi-solution problem. Therefore, Particle Swarm Optimization (PSO) algorithm is used to optimize the controller parameters to obtain satisfactory control performance based on the engine’s LPV model. Numerical simulations show that the thrust estimator can acquire smooth and accurate estimating results when sensor noise exists.The optimal controller can receive desired control performance both in steady and transition control tasks within the engine working states above the idle,verifying the effectiveness of the proposed DTC architecture’s application in thrust direct control problem.

1. Introduction

In the aircraft designing process, the thrust matching between engine control system and flight control system is a significant procedure. A good match will allow the engine to provide the proper thrust required by the aircraft, which has a great influence on the flight performance.Traditionally,the flight control system and the engine control system are designed separately.Thrust demand is firstly calculated by the flight control system.It is converted to shaft speed command and pressure ratio command, as these two control variables are usually considered the most related engine parameters to thrust. After that,the engine control system will control the engine states according to the engine states command given by the flight control system and the thrust will be controlled indirectly. However,such indirect thrust control structure will lead to great error between desired thrust and real thrust. First of all, turbofan engine performance varies from engine to engine due to manufacturing tolerances, ageing, and deterioration. The off-line designed control program is not customized for each engine,which means the control program is not accurate itself and will cause internal error. Secondly, with the degeneration of the engine, the same engine’s thrust usually changes at the same Power Lever Angle (PLA) in different flight cycles. Because of the inaccurate control of thrust,the pilot needs to manually adjust the flight attitude based on experience, which increases the pilot’s workload. For aircraft with multiple engines, the inconsistency of engine thrust will even make the aircraft yaw. The integrated flight & propulsion system will correct the yaw by adjusting the aircraft’s tail rudder, while this will increase the resistance and fuel consumption of the flight and reduce economy efficiency.If thrust demand can be delivered to the engine, in which thrust can be controlled directly and precisely, the problems discussed above can be solved.

Over the past two decades, direct thrust control has come into people’s sight. A workshop sponsored by NASA to identify technology development claimed needs for reducing pilot workload and increasing autonomy concerning the operation of aircraft engines.Based on the needs, Ring and Henriksson developed the concept of thrust control. A Kalman filter is used to estimate thrust and the thrust control is included as an add-on to a robust shaft speed control concept. Litt et al. proposed a thrust control system with a double-loop architecture. The outer loop calculates the error between actual thrust and thrust demand. The inner loop controls fan speed according to the thrust error. Chen et al. added a limit protection controller into the thrust tracking controller.However,in these methods, the essence of indirect thrust control is not completely changed and the complexity of the engine control system is somehow increased. Also, these methods are used in single-variable turbofan engine control. When the number of control variables increases, it is difficult to decide the best combination of control variables. In order to control the thrust directly and apply more control variables, Zhou et al. proposed an improved multivariable predictive control algorithm, in which thrust is directly controlled by a twovariable integrated control system. However, in this method,in order to make the number of control variables and controlled variables equal, the compressor surge margin SMis also considered as a controlled variable. It is unrealistic for the pilot to provide reasonable SMcommands during the flight attitude control process, which means application value of the method requires further discussion. Nikolaidis et al. proposed an advanced constraints management strategy for real-time optimization of gas turbine engine transient performance using model predictive approach,in which the thrust can be controlled directly and the strategy is capable of achieving the optimal and safe operation for the engine at different flight conditions. While the choosing of prediction length and control horizon has a great influence on the control effect,the computational burden of the algorithm may become unacceptable. From a practical point of view, it is urgent to develop a novel engine direct thrust control architecture which can be applied to multivariable turbofan engine. The architecture should possess the ability to estimate accurate thrust and give out optimal control strategy with small computational burden.

In the proposed DTC architecture, an accurate mathematical model is needed for controller and thrust estimator design.The LPV approach is considered to have innate advantages to characterize strongly nonlinear systems, in which system matrices affinely depend on time-varying parameters. By establishing an engine state-space model in affine LPV form,the strong nonlinearity of the system can be appropriately expressed. Besides, the calculation speed can be guaranteed due to the tiny storage space requirement of the affine system matrices. Because control variables are more than controlled variables, there are infinite combinations of solutions for the same control target. The existence of the multi-solution problem makes finding the optimal controller parameters according to specific criteria necessary.A large number of Meta-heuristic Global Optimization(MGO)algorithms is introduced into gas turbine engine controller optimization.The representative ones among these MGOs are Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Ant Colony Optimization(ACO), Invasive Weed Optimization (IWO), and Bee Colony Optimization (BCO). Liu et al. applied linkage learning genetic algorithm in Gas Turbine Engine (GTE) controller gains tuning and generated the optimization results for runway conditions in different flight conditions. Jafari et al. applied competent genetic algorithm, PSO and differential evolution algorithm in gains tuning of aero-engine and wind turbine.The results show that MGO algorithms performs much better in searching the optimal control parameters combination than trial and error manually. PSO is a kind of optimization algorithms inspired by individuals’social behavior in nature which is maturely developed and easily to be used in optimization problems with defined dimensions.Based on the PSO optimization algorithm,the controller can realize Multi Input Single Output (MISO) control with a satisfying control response.The controller parameters will also be formed into affine LPV form.Based on the parameter varying controller,thrust can be controlled in the full engine operation state above idle both in the transient and steady control tasks.

However, thrust is an unmeasurable output parameter.Thus, in order to calculate actual thrust to realize thrust control,a thrust estimator is needed.A variety of thrust estimators have been proposed,in which Kalman filter is often used in turbofan engine thrust estimation. In these methods, engine parameters are used to estimate thrust. However, due to the characteristic of Kalman filter, prior information about noise is required. Also, the oscillation characteristic of the filter is not suitable for the control problem.On-board real time modelling is also a promising solution for engine unmeasurable parameters estimation. Wei et al. proposed a hybrid Wiener model for on-board modeling of gas turbine aero-engines over the life cycle, which can estimate both steady and transient thrust over the engine life cycle.However,dependability,reliability and high-fidelity are still challenges for the on-board modeling of gas turbine aero-engines. Also, real-time calculation is also a difficulty in the use of on-board modeling.In order to reduce the complexity of model calculation and ensure the stability and robustness of the estimated value under the measurement noise, robust LPV Hfilter is introduced. If an LPV approach is used, it may happen that the change of LPV parameters will destabilize the Hfilter error estimation system. The error estimation system needs to be proved to be AQS and satisfy the Hperformance index γ in the whole parameter box. Yang et al. proved the affinely quadratically stability based on the assumption that the system is stable when the time-varying parameter ρ is at average value ρ. It is not enough to prove the stability in the whole parameter box. This paper generalizes the theory and relaxes the selection criteria of the performance index γ.The proposed filter improves the reliability of the DTC architecture under the existence of noises and model uncertainty.

This paper is structured as follows.In Section 2,the overall view of the proposed DTC architecture is presented. In Section 3, the affine LPV model of the engine is established. In Section 4, a thrust estimator based on robust LPV Hfilter is designed, and the AQS of error estimation equation in the entire parameter box is proved. In Section 5, a MISO optimal controller designing method based on the PSO algorithm is proposed for thrust direct control. Numerical simulations are conducted to verify the proposed DTC architecture’s effectiveness in Section 6 and conclusions are provided in Section 7.

2. System architecture

The proposed DTC architecture is shown in Fig. 1, which is composed of the optimal controller, the thrust estimator and the engine. The input of the engine is control variable u,while outputs are measurable engine output y and unmeasurable output thrust F. The engine state-space model is established as an LPV system, which can calculate measurable output yaccording to the current estimated state x. An LPV Hfilter estimates the current system state xaccording to the deviation ybetween engine output y and estimated output y.Here,estimated state xinstead of x measured by sensors is used to calculate ^F,as the measured state is unsmooth under sensor noise.Using x to calculate ^F will reduce the control quality greatly and cause the system to oscillate. With ^F and thrust demand rconverted from PLA, thrust error eis calculated as the optimal controller input. Based on the PSO algorithm, the optimal control parameters can be obtained.The control variable u is calculated to eliminate thrust error e.In the proposed system, both the filter and the optimal controller parameters are designed offline and organized into affine LPV form,which can be calculated rapidly with parameter vector ρ in actual use.Therefore, the DTC architecture proposed in this paper is an offline design online control technology with low storage information, which has high engineering application value. With the utilization of this system,tracking control of unmeasurable thrust F can be achieved and the Hfilter can reduce the influence of sensor noise, which enhances the robustness of the controller.

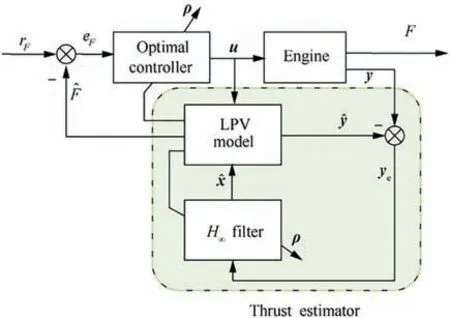
Fig. 1 DTC system architecture.

3. Linear parameter varying model of engine

In this paper, a two-spool military turbofan engine is discussed,in which the nozzle area Acan be adjusted.The thrust F is the most important engine performance parameter determined by the engine state. It is the controlled variable of the DTC architecture.As the fuel consumption Wand nozzle area Aare the main control variables to decide the engine state,they are selected to be the control variable u.

Considering the strong nonlinearity of the engine, the engine model is established as an LPV system. The model is established at the ground point,and control tasks at high altitudes can be realized by similar conversion.

3.1. System equations in affine LPV form

Consider an engine system as follows

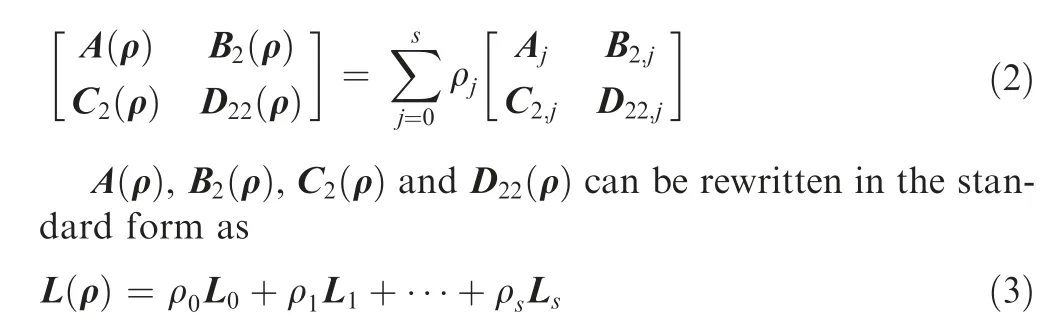
3.2. Selection of parameter vector ρ

The dynamic characteristics of the engine discussed in this paper varies greatly with nand A. For the Aand Aat ground points, we select 85 steady-state points with equal intervals in the engine working range of n, separately.At these steady-state points, parameters of A（ρ ）, B（ρ ）,C（ρ ） and D（ρ ） are calculated by partial differentiation method and approximated by a third-order polynomial model as

Elements in parameter matrices for n<0.939 and n≥0.939 are shown in Table 1 and Table 2.

4. Thrust estimator based on robust LPV H∞filter

As for DTC control problems, a thrust estimator is needed.Thrust is closely related to the system state nand n. Also,the adjustment of control variables Wand Awill change the current thrust. Therefore, the system state variable x and control variable u are selected to establish the LPV model to estimate thrust. Besides estimating the unmeasurable thrust,the system is required to be robust. As external interference exists,the controller is unable to guarantee the control quality of the closed-loop system. The robust LPV Hfilter is designed to estimate unmeasurable thrust and ensure the robustness against the sensor noise within the whole parameter box.

Fig. 2 Parameters of system matrix at A8，min

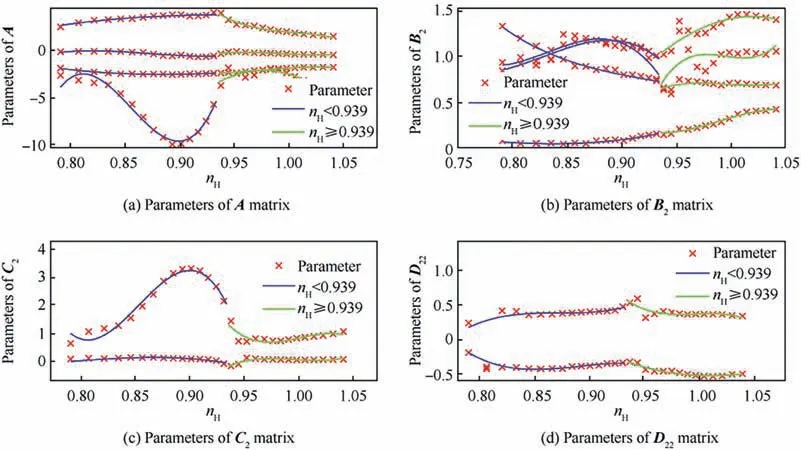
Fig. 3 Parameters of system matrix at A8，max

Based on the LPV model of the engine,an estimation equation of Hfilter with the similar mathematical form of Kalman filter is firstly established as

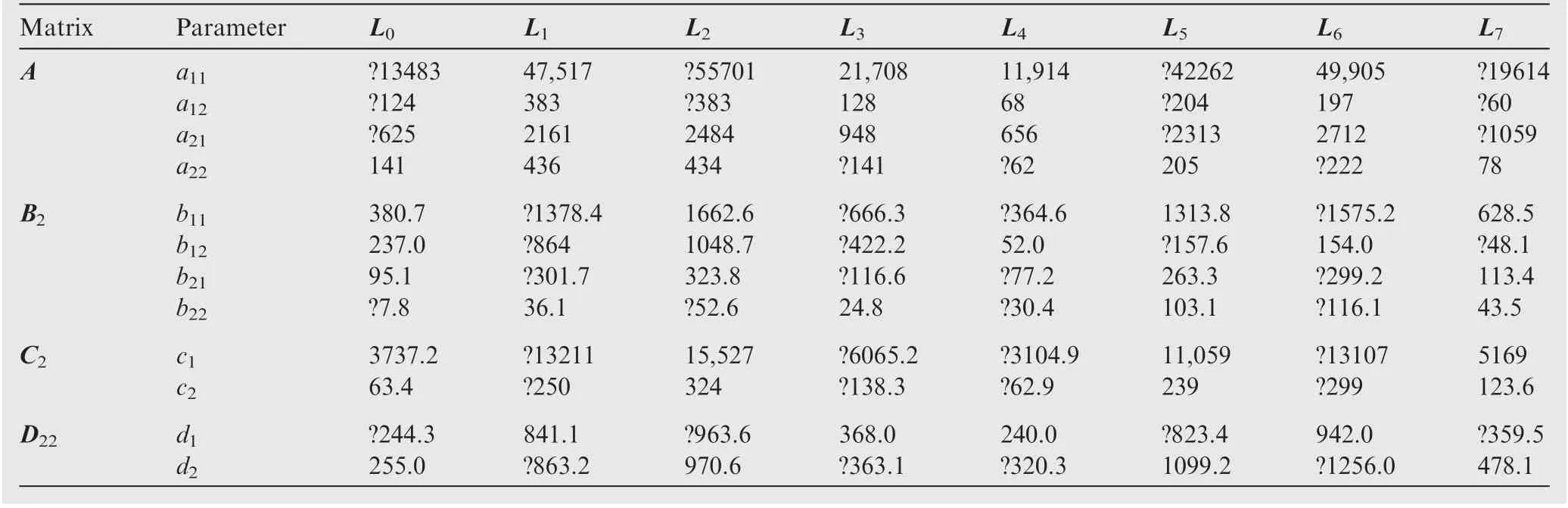
Table 1 Parameters of LPV model at ground point (nH <0.939).

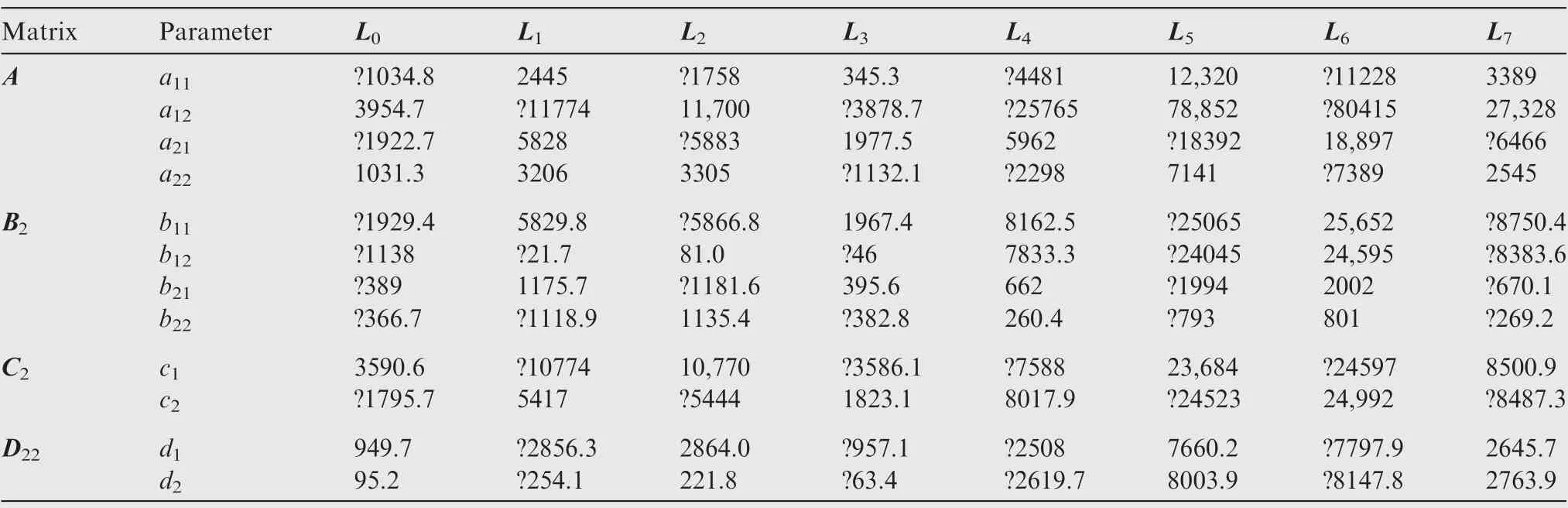
Table 2 Parameters of LPV model at ground point (nH ≡0.939).

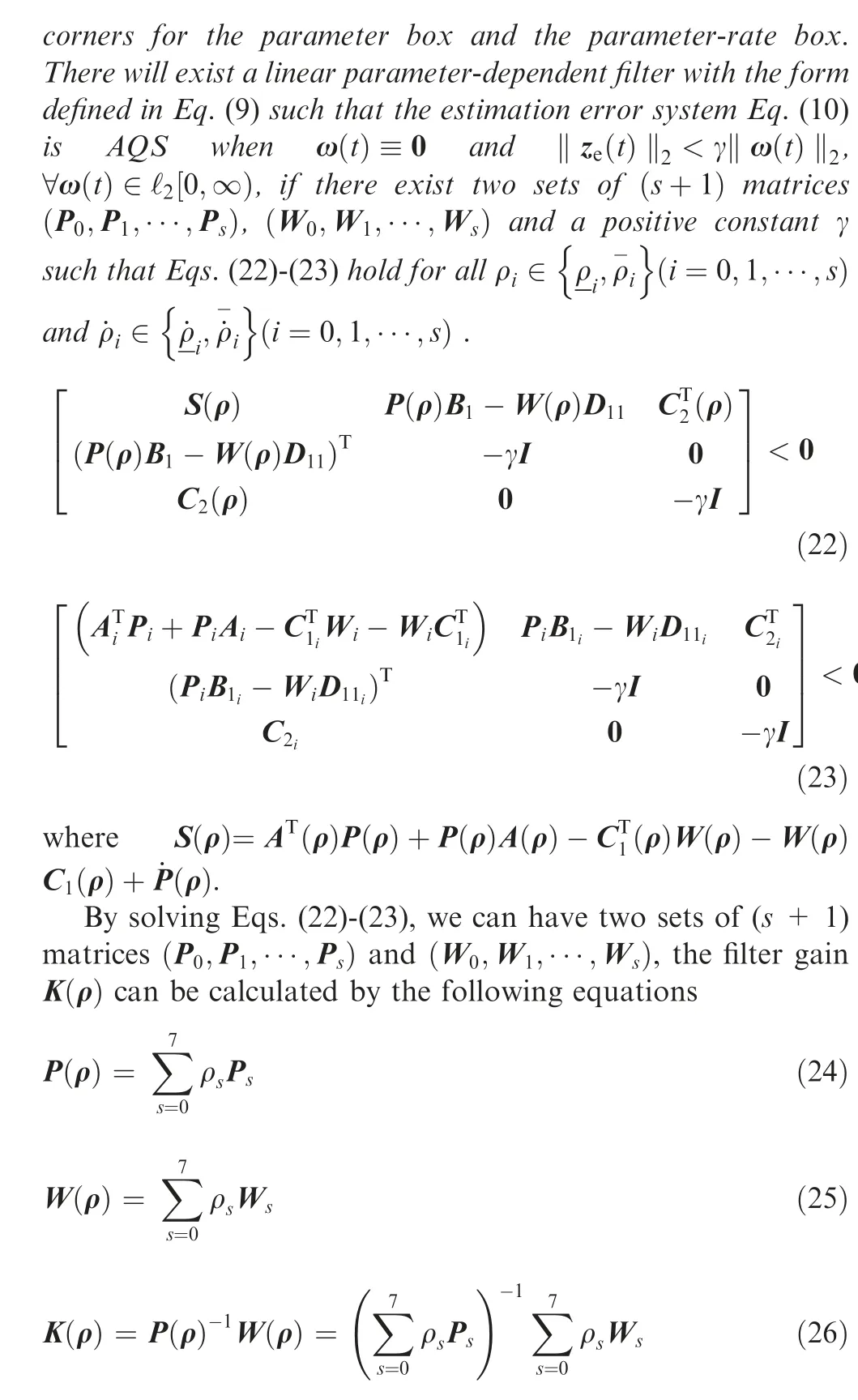
5. Optimal controller design

The optimal controller of the DTC architecture has two input variables and only one output variable. The traditional linear robust controller design method is not suitable for MISO dynamic system.As system matrices are non-square,determining of the controller parameters is an overdetermined problem.The process of finding MISO controller parameters is considered as solving an optimization problem.Particle Swarm Optimization (PSO) algorithm is a typical intelligent optimization algorithm and we will use it to select the most suitable parameters of the optimal controller.

5.1. Control law design

5.2. Controller parameter optimization based on PSO

Traditional multivariable controller design methods based on linear system require system matrices to be non-singular.However, in the proposed DTC architecture, the C（ρ ） is a 1×2 matrix, which makes J（ρ ） a 6×8 matrix. Because of the existence of the overdetermined equation,the solving of controller parameters will become a multi-solution problem. When we try to figure out uby solving Eq. (33), the controller parameters are not unique.

PSO is a stochastic evolutionary computation technique used for optimization inspired by individuals’ social behavior in nature. Compared with other optimization algorithms,PSO has fewer hyperparameters, and there is no need to consider the relevant gradient information. Also, natural real number coding is suitable for controller parameters optimization.

A set of particles represent the individuals seeking the optimal controller parameters, the dimension of which represents the number of the controller parameters to be optimized. At first, in the search space, particles are randomly initialized.Then,each particle represents a possible solution with a fitness value to rank its quality and select the best solution. The particles are supposed to move according to the Eqs.(36)and(37)until the ending condition is satisfied.

When fitness value J is less than a certain value or the iteration numbers reaches the upper limit, the search ends.

The process of searching the optimal controller parameter can be summarized in Algorithm 1.

Algorithm 1. Control parameter optimization algorithm Step 1 Initialization of the first equilibrium point Let k ∈1，2，...，85［］ represents the kth equilibrium point divided in Section 3.2.Initialize particles’ initial position of the 1st equilibrium point by uniformly sampling within the range of xid，min，xid，max■■.Step 2 Optimization for controller parameters For k ∈k1，k2，...，kmax［］Get system matrix A（ρk）, B2（ρk）, C2（ρk）, D22（ρk） of the present equilibrium point.According to the fitness value J, find the optimal controller parameters at the kth equilibrium point using PSO algorithm until reach the ending condition.Step 3 Fitting controller parameters into affine LPV form Fit the six parameters of F（ρk）into a three-order polynomial at A8，min and A8，max, respectively.Rewrite the polynomial into LPV affine approach according to Eq. (8).Notes: To make the fitting curve smooth, when k>1, the initial position of each particle is equal to the optimal position of the last equilibrium point.

The searching and fitting results of optimal controller parameters are shown in Fig.4.The forks represent the parameters of matrices F（ρ ）.At each equilibrium point,there are six forks in total,the number of which is equal to that of the controller parameters. The blue line and green line are the fitting results of the six parameters when n<0.939 and n≥0.939, respectively. As we can see, the fitted curve is quite smooth,which can avoid the abrupt change of controller parameter and ensure the quality of transient control in the full engine state above idle.

6. Simulation and analysis

Fig. 4 Controller parameter varying within nH range

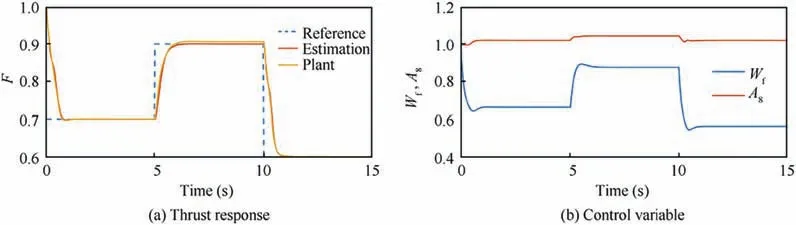
Fig. 5 Transient control simulation based on component level model (altitude H = 0 m, Ma = 0).

In Fig. 5(a), the blue line is the thrust reference signal, the red line is the estimated thrust calculated by robust LPV Hfilter and the orange line is the real thrust output of the plant.It can be noticed clearly that when the thrust command varies between 0.6 and 1.0,the controller can make the thrust quickly tracking the command. Simulations of three steady points are performed in order to showcase the accuracy of the thrust estimator and the reliability of the controller in the whole parameter box above idle. From 0 to 5 s, thrust command is 0.7.From 5 to 10 s, the thrust command is 0.9. From 10 to 15 s,the thrust command is 0.6. During the transformation process between different steady points, the average rising time is 0.52 s, and overshoot is about 0.15%. Root Mean Squared Error(RMSE)between estimated thrust and real thrust within the entire control task is about 0.0069.In addition,by observing the change of control variable u in Fig. 5(b), there is no abrupt vibration over the whole control period. This validates that the proposed architecture solves the multi-solution problem of MISO control and achieves a satisfying control performance.The robust LPV Hfilter estimates engine state and unmeasurable thrust accurately.

Fig. 6 Transient control simulation adding Gaussian white noise (altitude H = 0 m, Ma = 0).

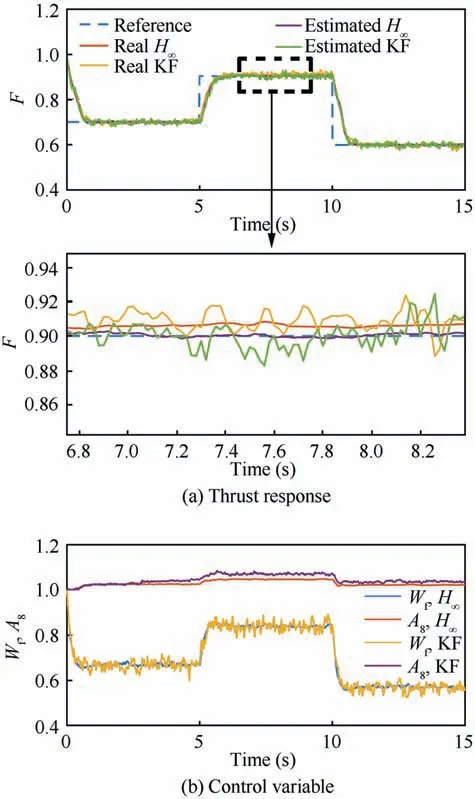
Fig.7 Transient control simulation adding Gaussian white noise with variance (0.02)2.

Now that we have proved the feasibility of the proposed architecture, to showcase the robustness of the system, test with sensor noise is done and results can be seen in Fig. 6.Here, it is assumed that the sensor noise is Gaussian white noise with the variance (0.02), which is shown in Fig. 6(e).Measured engine states with noise is shown in Figs. 6(b) and(c).

It can be seen clearly that under Gaussian noise, the vibration of sensor output is obvious.While with the help of robust thrust estimator, the estimated thrust in Fig. 6(a) does not jitter to such extent. RMSE between estimated thrust and real thrust of entire control task is about 0.0074. Compared to the RMSE without sensor noise,it rises only about 7.2%,indicating great robustness of the system. The control quality is not affected by noise.The rising time and overshoot are similar to the test without sensor noise.

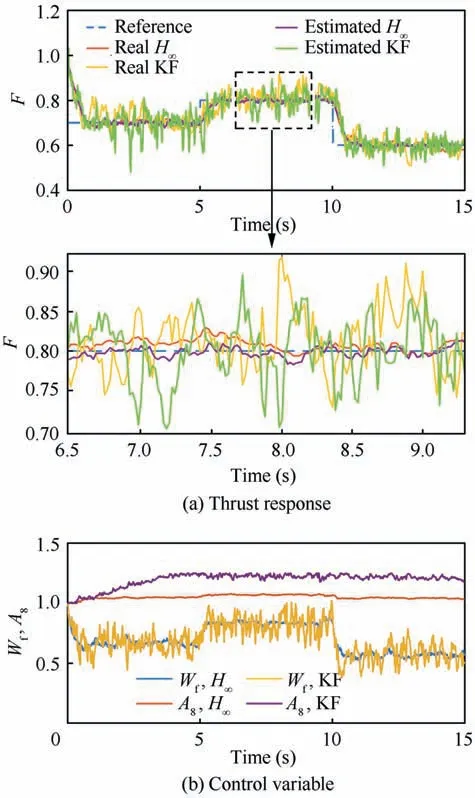
Fig.8 Transient control simulation adding Gaussian white noise with variance (0.10)2.

The comparison of the proposed thrust estimator with the Kalman Filter (KF), which is often used in the estimation of unmeasurable parameters in aero-engine control is shown in Fig. 7 and Fig. 8. Detail of estimation and control quality in a steady process is enlarged.

In Fig. 7, Gaussian white noise is generated with the variance (0.02). The green line in Fig. 7(a) is the estimated thrust calculated by Kalman filter, and the yellow line is the real thrust output of engine obtained by the DTC system with Kalman thrust estimator. RMSE of the proposed system between estimated thrust and real thrust in the entire control period is 0.0068. While RMSE of the system using the Kalman filter as thrust estimator is 0.0167, which is two times of that of the proposed system. In the detail picture in Fig. 7(a), we can see that the control results of the system using robust LPV Hfilter is much smoother than that of the system using the Kalman filter. In Fig. 8, when white noise variance is set to(0.10), RMSE of the proposed system is 0.0230. However,the RMSE of the system using the Kalman filter is 0.0868.In Fig. 8(b), the control variable of the system using the Kalman filter has a continuously increasing trend.The simulations in Fig.7 and Fig.8 show that the Hfilter is much more suitable for the application of the thrust control problem than the Kalman filter. This is due to the fact that Hfilter can give much smoother results than Kalman filter. In addition, when the prior information about Gaussian white noise is accurate,the accuracy of the Kalman filter cannot be ensured.When the noise is not ideal,Gaussian white noise or prior information is unknown, the Hfilter usually provides more reliable estimation results.

7. Conclusions

(1)In this paper,a novel DTC architecture for a two-spool turbofan engine based on engine affine LPV approach is proposed. First, an LPV model is designed to characterize the nonlinearity of the turbofan engine. Then, a thrust estimator based on improved robust LPV Hfilter is used to estimate thrust for control problem. Next, an optimal controller is designed to solve the multi-solution thrust direct control problem with two control variables. Both the estimator and the controller are designed in affine LPV form with the same parameter vector ρ of the engine model. The numerical simulation of the proposed DTC architecture is performed on the Component Level Model (CLM) of the two-spool turbofan engine.

(2)For the robust LPV Hestimator,the thrust estimation error system of is proved to be AQS and satisfies Hperformance index γ in the whole parameter box by relaxing the selection criterion of γ. The derivative of parameter vector ρ is considered as well in the proof process. Compared with the Kalman filter, robust LPV Hfilter is more suitable for the thrust control problem since it can provide smoother estimation results, especially when prior information about measurement noise is unknown.

(3) Based on the estimated thrust, the MISO optimal controller realizes thrust control of the two-spool turbofan engine.To address the multi-solution problem,PSO algorithm is used to search for optimal parameters of the controller at each equilibrium working point. The controller parameters are formulated in the LPV form with the same parameter vector ρ as the engine model. Applying the optimal controller, the whole system can achieve satisfactory response in thrust control tasks.

(4) Numerical simulations of the proposed turbofan DTC architecture at the ground point shows that thrust estimation error in the full working state is at a very low level. The proposed architecture can realize thrust direct control both in transition and steady control task with desired control quality and indicates excellent robustness when sensor noise exists.Due to the fact that the filter gain K（ρ ） and the controller gain F（ρ ） are all off-line designed. When the DTC architecture is online used, the K（ρ ） and the F（ρ ） can be obtained only by interpolating according to the engine state. The current estimated thrust and control quantities within the operation cycle can be calculated by multiple the gain with engine states, commands and measurable outputs. The computational complexity T（n ） = O（1 ） will not increase when the control task or engine states changes, which means the computation burden of the proposed DTC architecture is extremely low.

(5)The novelty of this work is to give a brand-new solution to the DTC problem of a multivariable turbofan engine. A MISO architecture of thrust control is firstly introduced,which is instructive for other similar direct thrust control research.However, there are still limitations. Frist of all, the accuracy of thrust estimating depends on the accuracy of modeling.Secondly, when the engine degenerates, the off-line designed model will become inaccurate. Creating a more refined model in the whole envelope is meaningful. Therefore, more engine parameters such as mass flow, turbine-exit temperature and degeneration parameters can be added into the modeling in order to improve the accuracy of modeling.On-board real time model for gas turbine engine can also be used to estimate thrust. In the future, we hope to realize the DTC architecture in the full envelope.With the increasing trend of engine control variables,more control variables can be added into the optimal MISO controller. Furthermore, the protection module can be considered in the DTC architecture, some safety limitations(over-speed, over-temperature, compressor surge margin,etc.) should also be taken into consideration. This would become an important research point in the next stage.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work was supported by the National Science and Technology Major Project, China (No. 2017-V-0004-0054).