A theoretical method for solving shock relations coupled with chemical equilibrium and its applications
Zijin ZHANG, Chihyung WEN, Wenshuo ZHANG, Yunfeng LIU,*,Zonglin JIANG
a Department of Aeronautical and Aviation Engineering, The Hong Kong Polytechnic University, Hong Kong, China
b Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
c School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China
KEYWORDS Chemical equilibrium;Detonation;Dissociated air;Shock relation;Theoretical solution
Abstract In this study, a theoretical method is proposed to solve shock relations coupled with chemical equilibrium.Not only shock waves in dissociated flows but also detonation waves in combustive mixtures can be solved. The global iterative solving process is specially designed to mimic the physical and chemical process in reactive shock waves to ensure good stability and fast convergence in the proposed method.Within each global step,the single-variable equations of normal and oblique shock relations are derived and solved with the Newton iteration method to reduce the complexity of the problems,and the minimization of free energy method of NASA(National Aeronautics and Space Administration) is adopted to solve equilibrium compositions. It is demonstrated that the convergent process is stable and very close to the real chemical-kinetic process, and high accuracy is achieved in the solutions of normal and oblique reactive shock waves. Moreover, the proposed theoretical method has also been applied to many problems associated with reactive shocks,including the stability of oblique detonation wave,bow detonation over a sphere,and shock reflection in dissociated air.The great importance of using chemical equilibrium to theoretically predict the theoretical range of the wedge angle for a standing oblique detonation wave (the standing window of the oblique detonation wave), the stand-off distance of bow detonation wave and the transition criterion of shock reflection in dissociated air with high accuracy have been addressed.©2021 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
1. Introduction
Shock waves,including normal shock waves and oblique shock waves,are common physical phenomena in gas dynamics,and also basic flow structures in supersonic gas flows. In some circumstances, chemical reactions will occur after the compression of a shock wave. Moreover, chemical reactions behind a shock always have significant effects on the propagation of the shock wave. For example, when a shock wave propagates in a premixed combustible gas, such as the hydrogen-air mixture, violent and fast combustion will be induced by the hightemperature and high-pressure environment just behind the shock, and the shock will be accelerated in turn by the chemical heat release. Therefore, a shock wave strongly coupled with combustion, called a detonation wave, is formed and propagates in a self-sustaining way with a very high speed.Research on the detonation phenomenon is not only a scientific issue, but also the base of development of the high efficiency propulsion systems using detonation waves for airbreathing hypersonic aircrafts.
Coupling of shock waves and chemical reactions is also an important mechanism in high-temperature real gas effects of air and carbon dioxide, when the spacecraft return to the earthand landers enter the Mars atmosphere,respectively.Oxygen and nitrogen molecules in air will be dissociated into atoms or recombined into oxynitrides by compression of the strong shock wave formed ahead of the blunt body flying at an extremely high speed. Thereafter, due to the change of physical properties across the shock and the thermal effects of chemical reactions,shock relations will become quite different from the classical ones derived from the ideal-gas theory.As a result, the aerodynamic performances of spacecraft will be deviated from the predicted values in an ideal-gas environment, which is important for the control and safety of spacecraft.
Researches of shock waves coupling with chemical reactions have been carried out by experimentsand numerical simulations.However, despite the complexity of the problems, theoretical studies still play an important role in understanding the inherent mechanism, and in predicting shock phenomena efficiently with a satisfactory accuracy, such as shock reflections, shock interactions, etc. Problems of shock waves coupled with chemical reactions can be solved mainly by three approaches according to different physical hypotheses and approximations. The most convenient approach is to assume that mixture compositions and specific heat ratios before and behind the shock wave are respectively known,and the mixtures before and behind the shock wave can be dealt with the ideal-gas theory.This method is simple and can be solved analytically. However, it is not accurate enough based on the following facts. Firstly, due to the excitation of vibrational degrees of freedom under high-temperature conditions behind the shock wave, many physical properties of the mixture depend on the temperature. As a result, they are unknown before solving. Secondly, the heat effects are also unknown before solving due to forward and backward reactions, which are dependent on the pressure and temperature behind the shock.Thus,the choices of the values of fixed specific heat ratio and reaction heat are so subjective that the solution of shock wave coupled with chemical reactions by this method is not reliable enough in the engineering applications,when high precision is needed.
Another approach is the closest to the true physics by solving chemical kinetics(for example, Refs.). Assuming finite chemical reaction rates, the chemical non-equilibrium processes are induced by the high-temperature conditions behind the shock wave, which results in non-uniform flow properties behind the shock. The mixture properties are determined by the local mixture composition and temperature. Although it is reasonable to adopt this chemical non-equilibrium method to solve the problem, it is quite complex and difficult to achieve fast solution,especially when solving the oblique shock waves.Moreover,solution using this chemical non-equilibrium method depends on the time scale of the problem(i.e.,the ratio of characteristic chemical reaction time to the characteristic flow time) and it is not general enough. Nevertheless, as one ultimate limit of chemical non-equilibrium processes, the assumption of infinite chemical kinetics is widely used in previous theoretical analyses.Hence, the third approach is to assume infinite chemical kinetics and solve the reactive shock waves using chemical equilibrium. In many cases, such as gas detonation, the time scale of chemical reaction is always far smaller than that of flow, resulting in the reasonable assumption of chemical equilibrium. Further, the theoretical solution of chemical equilibrium can be obtained easier,not as complex as chemical non-equilibrium, and preserves the advantage of fast solution.
In the past decades, NASA (National Aeronautics and Space Administration) has developed a chemical equilibrium computer program,CEA(Chemical Equilibrium with Applications), to calculate chemical equilibrium compositions and properties of complex mixtures and it has been extended to many applications, including calculation of theoretical rocket performances, Chapman-Jouguet detonation parameters,shock tube parameters and so on.Another GUI (Graphical User Interface) program used the same method of NASA,called Gaseq, has been widely used by engineers.However,the CEA program was initially designed to calculate the theoretical performances of the rocket engines. Only are normal shock waves coupled with equilibrium chemical reactions available.No solution of oblique shock waves is provided,that are also common and important in engineering and more complex.Last but not least,the CEA solution is obtained using of the multidimensional Newton iteration method that solves matrix equations. Hence, the derivatives of gas state variables should be derived and calculated under the chemical equilibrium assumption. The solution still involves rather complex iteration processes and its convergence is greatly dependent on the choice of the set of initial values.
In this study,a two-steps iterative theoretical method,using the single-variable Newton method to solve shock relations and the minimization of free energy method of NASA to solve equilibrium compositions, is proposed, which mimics the real reacting process and is therefore robust in convergence. Based on this method, several applications are discussed, including the calculation of detonation polar and the theoretical range of the wedge angle for a standing oblique detonation wave(the standing window of the oblique detonation wave),standing-off distance prediction for a bow detonation wave,and prediction of transition criteria of shock reflection in dissociated air.
2. Theoretical method and mathematical formulation
2.1. Physical problems and hypotheses

A shock wave, either a normal shock wave (Fig. 1(a)) or an oblique shock wave (Fig. 1(b)), coupled with thermal equilibrium and chemical equilibrium in multi-species gas mixtures is theoretically solved in this study. Notably in Fig. 1, p, T,ρ and u represent the pressure,temperature,density and velocity of the gas mixture, respectively; χis the molar fraction of species i(i=1,2,...,n,and nis the number of species considered in the mixture); θ and β are the wedge angle and oblique shock angle, respectively; subscripts 1 and 2 represent the flow states before and behind the shock wave,respectively;and subscripts n and τ denote the velocity components normal to and tangential to the oblique shock front, respectively. For example, for the detonation wave in hydrogen-air mixture,11 species (H, H, O, O, OH, HO, HO, HO, N, Nand NO) can be considered,and for the strong shock in air, 6 species(N,O,Ar,NO,N and O)can be considered.All parameters before the shock wave (Zone 1), including temperature,pressure, velocity and composition, are assumed to be known,and those behind the shock wave (Zone 2) are to be solved.
For each species, the perfect-gas equation of state is still satisfied. However, the gas is always not a calorically perfect one, due to the excitation of vibration degrees of freedom under high-temperature conditions behind the shock wave.As a result,the enthalpy of each species is a nonlinear function of temperature under the assumption of thermal equilibrium,and accordingly the specific heat ratio is a function of temperature as well.

2.2. Solving strategy
The problem of shock wave coupled with chemical equilibrium is complicated. The properties of the flow behind the shock wave, such as temperature, pressure, and velocity, are decided by the shock relations,while the shock relations are relative to the compositions behind the shock and the heat release of chemical reactions. Reversely, the equilibrium compositions of the mixture and the thermal effects of chemical reactions are dependent on temperature and pressure because of reversible reactions. Therefore, it is a problem with coupling of a large number of variables,including equilibrium compositions,temperature, pressure, velocity, etc.
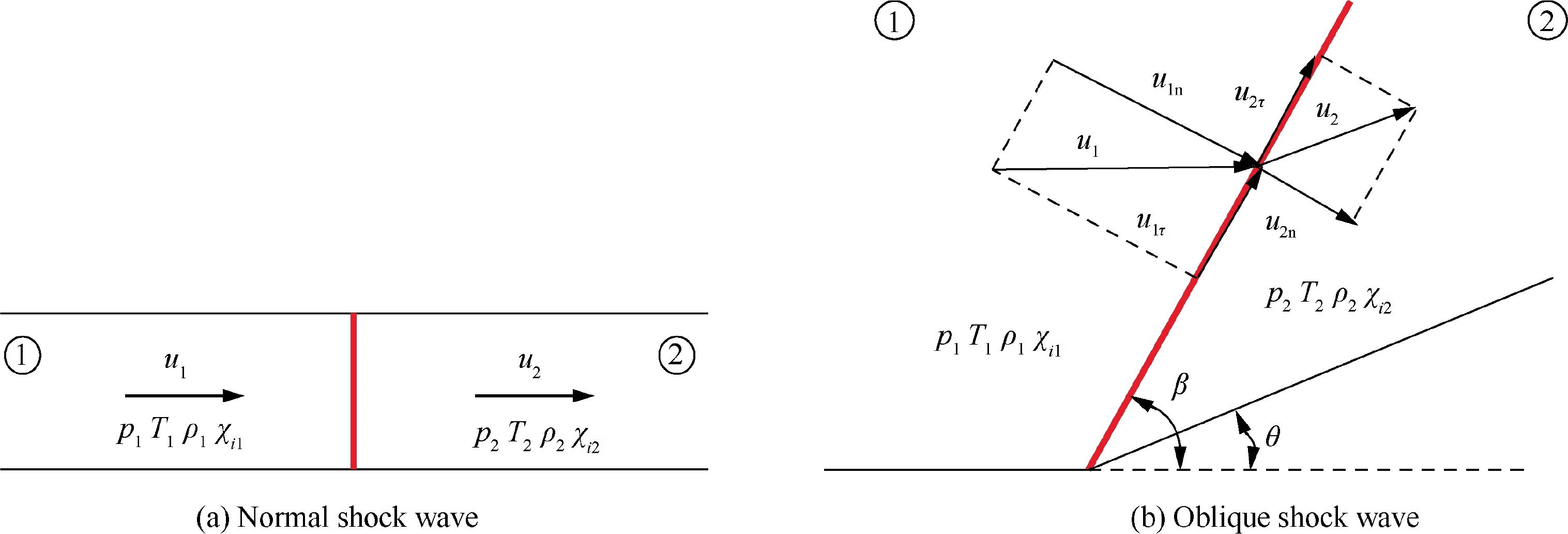
Fig. 1 Shock waves in multi-species gas mixtures.
To solve this problem, a physically reasonable and stable solving process is proposed in this paper based on the following physical facts. In the classical ZND (Zel’dovich-von Neumann-Do¨ring)structure of the detonation wave(Fig.2),the high-speed reactants are first compressed non-reactively by the shock wave. Then behind the shock, reactions are induced under the high-temperature and high-pressure conditions.With the mixture reacting gradually, the reactants are consumed, the products are produced, the temperature rises and the pressure drops gradually until chemical equilibrium. The reaction process is very fast and hence the reaction zone is very thin in the detonation wave. That is, the detonation wave is constituted by a non-reactive shock wave and a thin reaction zone. Therefore, the flow properties at an arbitrary position within the reaction zone are the medium solution of the detonation wave, and the flow properties behind the reaction zone are just the chemical equilibrium solution of the detonation wave. The solving process proposed in this paper is trying to mimic above chemical reaction process to obtain the equilibrium solution of shock wave coupled with chemical reaction,as shown in Fig. 3. Notably, superscripts (k) and (*) denote the kth global iteration value and the intermediate value in global iteration step, respectively.
In the solving process, the flow properties and the compositions(of reactants)before the shock are known at the beginning. At first, by assuming non-reactive, the compositions behind the shock are the same as those before the shock.Then,the iteration process begins.Step 1: the shock relations can be calculated iteratively with known compositions before and behind the shock and hence the temperature and pressure behind the shock can be determined.Step 2:with specific temperature and pressure,new compositions behind the shock can be calculated using the minimization of free energy method of NASA. With the new compositions of the mixture behind the shock, a new iteration can be processed until convergence is achieved.
In Fig. 3, the convergence criteria for the problem can be chosen as following,

Fig. 2 ZND structure of detonation wave in hydrogen-air mixture (before shock: 0.42H2 + 0.21O2 + 0.79N2, T1 = 300 K,p1=1 atm(1 atm=101325 Pa),u1=2500 m/s),calculated by a detailed chemical reaction mechanism.23
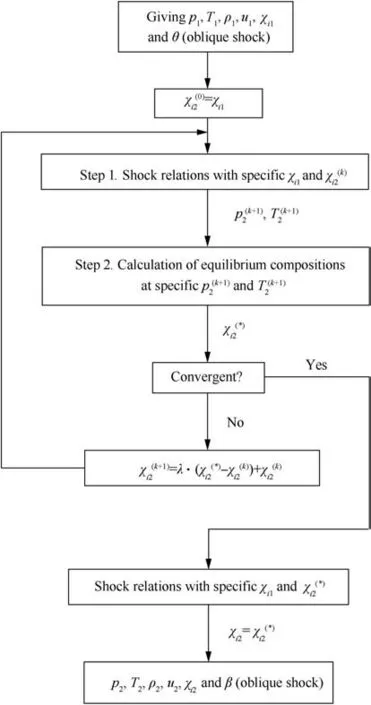
Fig. 3 Diagram of solving process.
Also presented in Fig.3 is a relaxation treatment adopted in the global iteration step,when updating the new compositions behind the shock,to avoid undesired oscillations in the solving process and to ensure stability and convergence.λ is the relaxation factor and can be set as 0.4 empirically and conservatively. A brief discussion on the effects of λ value on the convergence process will be given later in Section 2.6.1. It is easy to know that above solving process cannot simulate the exact ZND structure,but it is very close to the ZND structure(this will be discussed detailedly in Section 2.6). Notably, it is not necessary to reproduce the exact ZND structure, because only the equilibrium solution of the shock wave is pursued.Thus,the physical bases of the solving process in Fig.3 ensure that the iteration process is stable and easy to achieve the solution convergence.
2.3. Normal shock relations with known compositions
In the solving process of the problem,the shock relations with known mixture compositions before and behind the shock wave need to be calculated in each global iteration step,namely the Step 1 in Fig.3.In this section,the method for calculation of normal shock relations is discussed first.All parameters of the mixture before the normal shock wave and the composition behind the shock wave are assumed to be known,and other parameters behind the shock wave are to be determined, such as pressure, temperature and velocity (see Fig. 1(a)).
As the compositions before and after the shock wave are known,the gas constants of the mixtures Rand Rare known as well.From the gas dynamic theory,the governing equations for this normal shock wave problem can be expressed as follow.
Continuity equation:

It is easy to know that in Eqs. (8)-(11), the unknown variables are ρ, p, Tand u. There are four unknown variables and four equations, thus the problem is well posed. Notably,from Eqs. (2) and (6), the specific enthalpy h(T) in Eq. (10)is a nonlinear function of T. Hence, Eqs. (8)-(11) cannot be solved analytically. A direct way to solve this equation set is to use the multidimensional Newton iteration method. However,it is still complex to solve the matrix equation and its convergence is closely dependent on the choice of the set of initial values. Consequently, to simplify the problem, an effort is made to reduce the order of the problem and to simplify the Newton iteration process in this paper.

Dividing Eq. (9) by Eq. (8) yields,where c(T) = dh/dTis the specific heat of the mixture at constant pressure behind the shock and it can be evaluated by Eqs. (1), (5) and (6). When uhas been solved, it is easily to solve Tby Eq. (14), ρby Eq. (8), and pby Eq. (11) with Tand ρ.
In order to show the advantage of the iteration method proposed in this section, an example of the function f(u) in the solving process of the normal shock wave problem with known composition behind the shock is shown in Fig. 4.The mixture before the shock is the equivalent hydrogen-air mixture:0.42H+0.21O+0.79N,and the mixture behind the shock is assume frozen(i.e.,the Step 1 in the first iteration of Fig.3 in the corresponding equilibrium solution). And the flow parameters before the shock are T= 300 K, p= 1 atm,u=2500 m/s(Ma=6.12).As illustrated in Fig.4,the function f concaves downward and there are two roots (Points A and B)for the equation f(u)=0.It is easy to know that Point A is the exact solution of the normal shock wave problem and Point B corresponds to the equilibrium state before the shock that is meaningless. Therefore, it is intuitive to set the initial iteration value near u= 0, such as u= 10 m/s. Then, the solution can be quickly approached by the Newton iteration process along the function f to Point A.As a result,the solving process is stable and the convergence can be easily achieved due to the good properties of the Newton iteration function f.
Consequently, the success in reducing the four-variable problem of Eqs.(8)-(11)into one equation with only one independent variable and the use of single-variable Newton iteration method, make the solving process of the normal shock wave problem with thermal equilibrium easy and reliable.
2.4. Oblique shock relations with known compositions
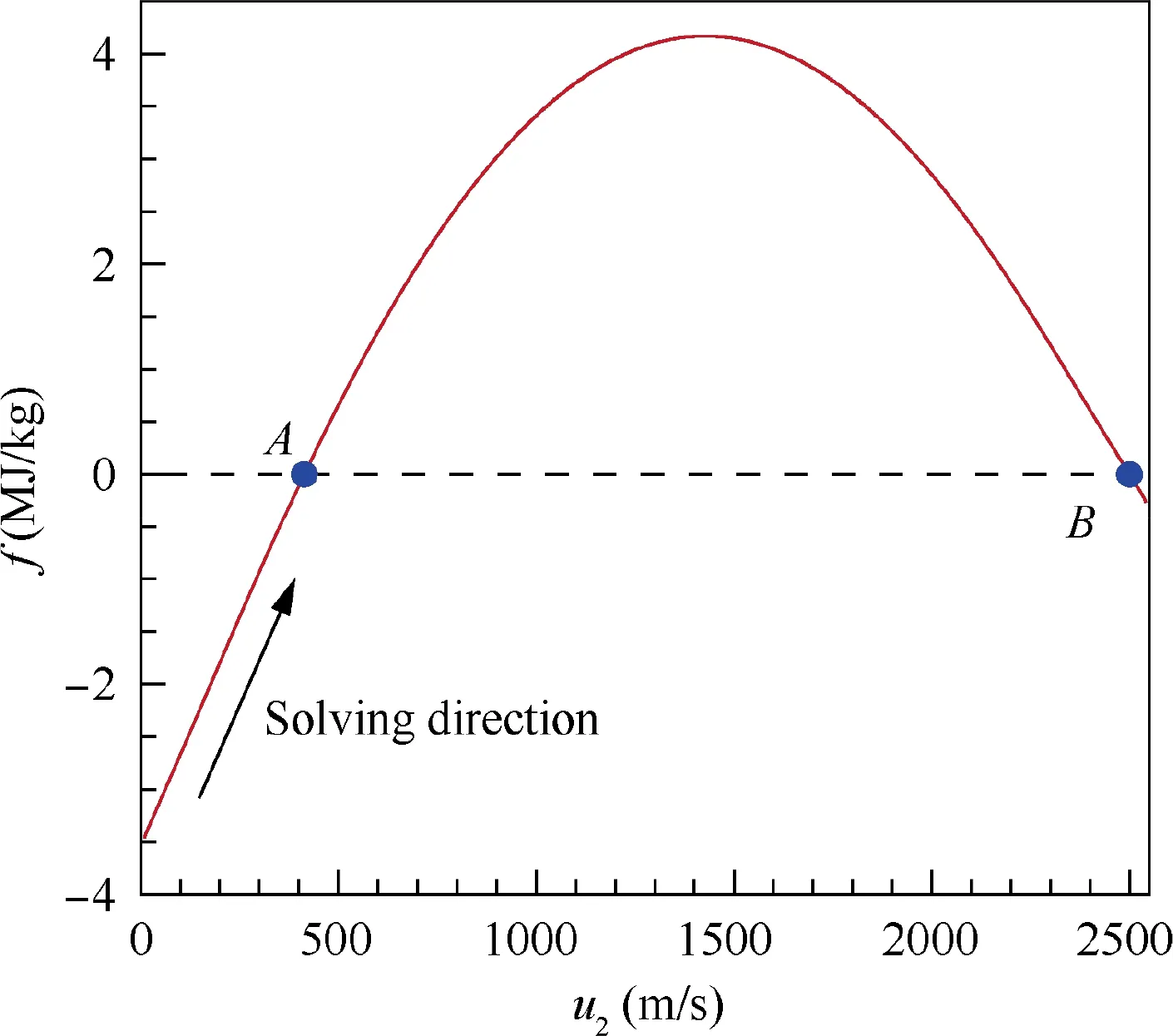
Fig.4 An example of function f(u2)in solving process of normal shock wave problem in hydrogen-air mixture (before shock:0.42H2 + 0.21O2 + 0.79N2, T1 = 300 K, p1 = 1 atm,u1 = 2500 m/s; behind shock: 0.42H2 + 0.21O2 + 0.79N2).
The same treatment as in Section 2.3 can be used to reduce the order of the oblique shock wave problem with known mixture compositions before and behind the shock wave, and to simplify and stabilize the solving process. Again, all parameters of the mixture before the oblique shock wave and the composition behind the shock wave are assumed to be known as well as the wedge angle θ, and other parameters behind the shock wave are to be determined, such as pressure, temperature and velocity (see Fig. 1(b)). From the gas dynamic theory,the governing equations for this oblique shock wave problem can be expressed as follow.
Continuity equation:

where βis the result of the kth iteration. To complete the solving process, the derivative of g can be easily derived by the derivative method for a compound function with Eqs. (25)-(27),
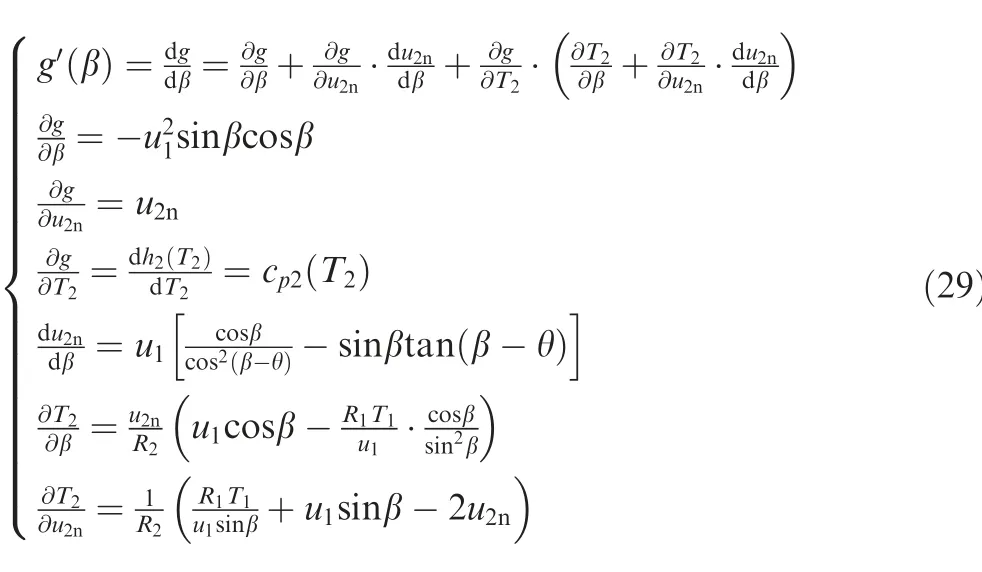
After β has been solved by Eqs. (25)-(29), the solutions of uand ucan be obtained by Eq. (26), ρby Eq. (18), Tby Eq. (25), and pby Eq. (11) with Tand ρ. Apparently, the derivation process is similar to that in Section 2.3, but more compound functions are involved.
Similarly, an example of the function g(β) in the solving process of the oblique shock wave problem with known composition behind the oblique shock is shown in Fig.5.The mixture before the shock is the equivalent hydrogen-air mixture:0.42H+0.21O+0.79N,and the mixture behind the shock is assume frozen again (i.e., the Step 1 in the first iteration of Fig. 3 in the corresponding equilibrium solution). The flow parameters before the shock are T= 300 K, p= 0.4 atm,u= 3270 m/s (Ma = 8), and the wedge angle is θ = 30°.As depicted in Fig.5,the function g concaves downward again and two roots (Points A and B) of the equation g(β) = 0 are found. The Point A is the weak solution of oblique shock wave, while the Point B is the strong solution. Generally, the weak solution, namely the Point A, is the natural oblique shock wave solution. Moreover, the shock angle β is always larger than the wedge angle θ.Thus,it is intuitive to set the initial iteration value βnear θ,such as β=θ+0.1°.The problem can be solved along the function g to Point A thereafter.The solving process is stable again and the convergence can be easily achieved due to the good properties of the Newton iteration function g. Notably, the strong solution of oblique shock wave may need to be solved in some specific problems,such as the asymmetrical Mach reflection. In this case, the initial iteration value of βcan be set near 90°, and then the problem can be solved along the function curve of g to Point B.
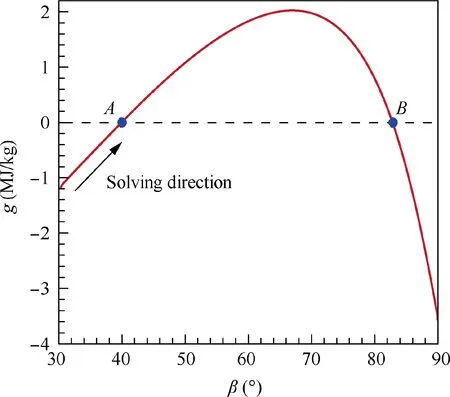
Fig.5 An example of function g(β)in solving process of oblique shock wave problem in hydrogen-air mixture (θ = 30°; before shock: 0.42H2 + 0.21O2 + 0.79N2, T1 = 300 K, p1 = 0.4 atm,u1 = 3270 m/s; behind shock: 0.42H2 + 0.21O2 + 0.79N2).
2.5. Calculation of equilibrium compositions at specific p and T
Another key step in each global iteration step in the solving process of the problem is to calculate the equilibrium compositions at a specified pressure and temperature,namely the Step 2 in Fig. 3. Given the initial compositions of the mixture (the reactants),the equilibrium compositions need to be determined under specified temperature and pressure.The minimization of free energy method of NASAis adopted in this paper.
The Gibbs free energy G of the mixture at pressure p and temperature T is given by,

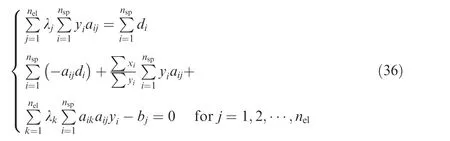
Notably,Eq.(36)can be easily derived from the summation of Eq. (35) or substituting Eq. (35) into Eq. (31). When xin Eq.(35)is solved,it can be set to be the new yfor the next iteration, until convergence.
2.6. Validations
2.6.1. Normal shock wave
In order to validate the proposed method in this paper, an equilibrium normal shock problem is examined first.The mixture before the shock is the equivalent hydrogen-air mixture(0.42H+ 0.21O+ 0.79N) with T= 300 K, p= 1 atm and u= 2500 m/s, and 11 species (H, H, O, O, OH, HO,HO, HO, N, Nand NO) are considered in the chemical equilibrium calculation.This kind of shock wave actually corresponds to an over-driven hydrogen-air detonation wave.Parameters behind the shock and the iteration error defined in Eq. (7) in the convergence process (λ = 0.4) are presented in Fig. 6. It is clearly observed that the convergence process of this method is stable and the parameters change monotonously to the convergent values. Further, the error decreases exponentially in the convergence process and the 10order of error is achieved within 30 iterations.Consequently,it takes less than 1 s to finish the iterations.
Notably, the relaxation factor λ is an important control parameter in the proposed method, and the convergence stability and speed are undoubtably affected by the chosen value of λ. To clarify this, the changes of post-shock temperature,Hmole fraction and iteration error defined in Eq. (7) during the convergence process of the present normal shock problem using different λ values are depicted in Figs. 7(a)-(c), respectively. Moreover, a summary of the iteration errors achieved after 30 iterations with different λ values is given in Fig. 7(d).As seen, when the λ value is too small (for example, λ = 0.1 or 0.2), the post-shock parameters monotonously converge to the corresponding equilibrium values, but the convergence process is rather slow. After 30 iterations, the iteration errors only reduce to about 10and 7 × 10for λ = 0.1 and 0.2,respectively, indicating a large number of iterations is needed to achieve the desired convergence accuracy with a rather small value of λ. As the λ value increases, the convergence process becomes fast and the iteration error after 30 iterations drops significantly. When the λ value increases to 0.6,an extremely small iteration error of about 10can be achieved via 30 iterations. However, if the λ value increases further, undesired oscillations of the post-shock parameters appear in the convergence process. As a result, the convergence process becomes slow again and tends to be unstable.For example, for λ = 0.8, the iteration error only reduces to about 4 × 10after 30 iterations. Taking both the convergence stability and speed into consideration at the same time,a range of λ = 0.4-0.7 is favorable for the present normal shock problem. Finally, a value of λ = 0.4 is suggested and used conservatively in this paper to ensure a good stability of the convergence process along with an acceptable convergence speed.
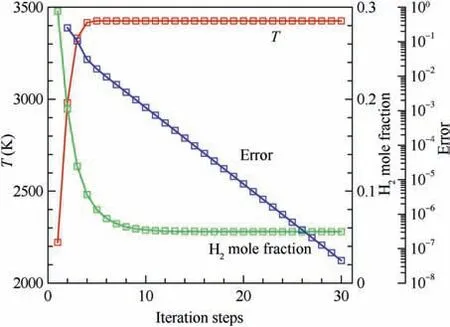
Fig. 6 Convergence process of normal shock problem (before shock: 0.42H2 + 0.21O2 + 0.79N2, T1 = 300 K, p1 = 1 atm,u1 = 2500 m/s; λ = 0.4).
The solutions of the final flow parameters and mixture compositions behind the shock are shown in Table 1 and Fig. 8,respectively.The ZND solutions calculated by a finite chemical kinetics are also presented for comparison. The detailed equations for calculating the ZND solutions are briefly introduced in the Appendix for clarity.The ZND solutions far behind the shock can be considered as the exact solutions of chemical equilibrium. The differences between the theoretical solutions in this paper and the ZND solutions are defined as the errors of the method proposed in this paper. Clearly seen, the errors of all flow parameters and mixture compositions behind the shock are less than 10,which means that for solving the normal shock problem coupled with chemical equilibrium, the precision of the proposed theoretical method is very high.
Additionally, in order to show the physical bases of the solving process described in Fig. 3, the convergence paths,from the frozen shock solution to the equilibrium shock solution are demonstrated in Fig. 9 and compared with the ZND solutions with a detailed chemical-kinetic process. It can be seen that the current theoretical convergence process does not exactly follow the ZND chemical-kinetic process (Fig. 9(b)). Nevertheless, the similar trend of the chemical reactions as the ZND solution is observed. The current p-T path(Fig. 9(a)) match that of the ZND solution well. Notably,the p-T path is important to the stability of the convergence process.In summary,the proposed solving process is of certain physical bases, which consequently ensures the good stability and fast convergence of the proposed solving method. This is also the initial intention to design such theoretical iteration method in this work (as discussed in Section 2.2).
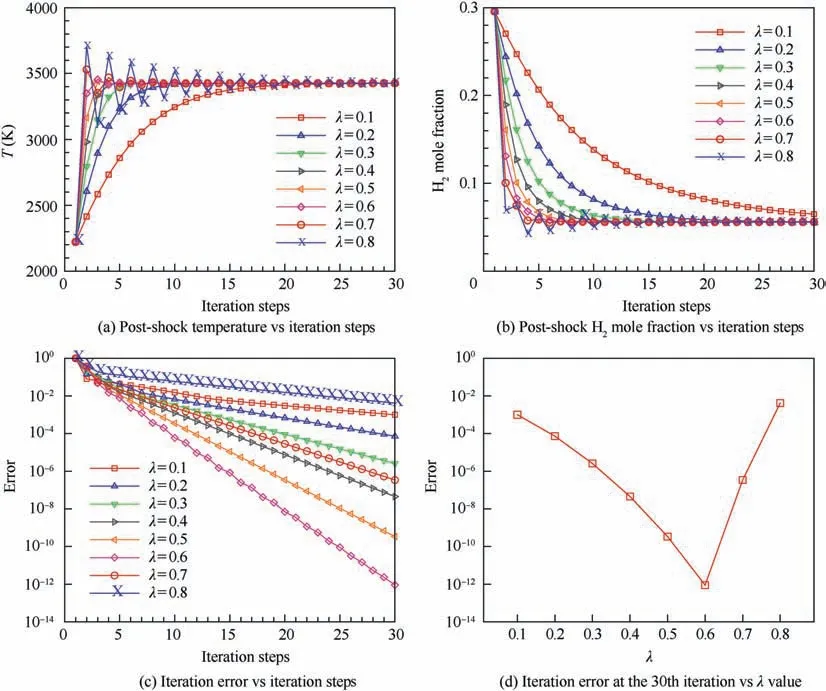
Fig. 7 Effects of λ value on convergence error and speed for normal shock problem (before shock: 0.42H2 + 0.21O2 + 0.79N2,T1 = 300 K, p1 = 1 atm, u1 = 2500 m/s).
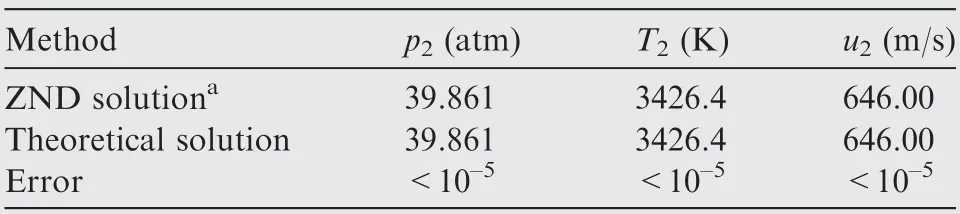
Table 1 Comparison of flow parameters behind normal shock waveinhydrogen-airmixture(beforeshock:0.42H2 + 0.21O2 + 0.79N2, T1 = 300 K, p1 = 1 atm,u1 = 2500 m/s).
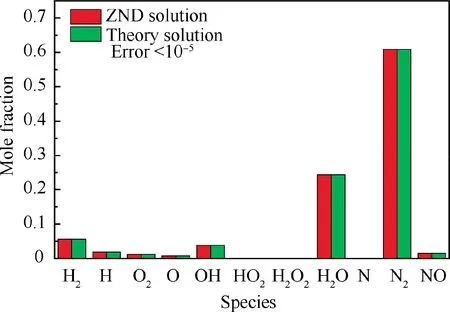
Fig. 8 Comparison of species compositions behind normal shock wave in hydrogen-air mixture (before shock:0.42H2 + 0.21O2 + 0.79N2, T1 = 300 K, p1 = 1 atm,u1 = 2500 m/s).
2.6.2. Oblique shock wave
The same validation process of the proposed theoretical method can be illustrated to the equilibrium oblique shock wave problem. An oblique shock wave in the hydrogen-air mixture (0.42H+ 0.21O+ 0.79N) with T= 300 K,p=0.4 atm,u=3270 m/s(Ma=8.0)and θ=30°is examined,and the same 11 species (H,H,O,O, OH,HO,HO,HO, N, Nand NO) are considered in the chemical equilibrium calculation. Obviously, this kind of oblique shock wave is actually an oblique detonation wave. Convergent solutions of flow parameters and mixture compositions behind the oblique shock are shown in Table 2 and Fig.10,respectively.As it is difficult to obtain the ZND solutions of oblique detonation for comparison, the CFD (Computational Fluid Dynamics)solutions with a detailed chemical reaction mechanism (via our in-house CE/SE code)are adopted and considered as the nominal exact solution, and the differences between the theoretical solution in this paper and the CFD solution are hence the errors of the proposed method. From Table 2 and Fig. 10, the maximum error of the proposed method is less than 2‰. The comparison of shock angle is shown in Fig. 11. Essentially, no difference between the theoretical shock angle and that of CFD is observed. Notably, although the CFD solution is extracted downstream the shock front as far as possible, it is still slightly deviated from the truly exact equilibrium solution with the limitation of the size of computational domain, leading to a slightly larger nominal relative error in the present equilibrium oblique shock problem as compared to that in the above equilibrium normal shock problem (<10). Nevertheless, high accuracy is demonstrated when solving the oblique shock wave problem coupled with chemical equilibrium once again.
3. Applications
3.1. Detonation polar and standing window for oblique detonation
The shock polar analysis is a simple and effective tool in theoretical studies of shock wave reflection phenomena and other shock/shock interaction problems.And it has been extended to analyze shock waves in ideal dissociating gases and in radiative gases.As for detonation waves,the shock waves coupled with fast combustion,there is no doubt that the polar analysis would play the same important role.Moreover,the theoretical range of the wedge angle for a standing oblique detonation wave, namely the standing window, can also be obtained from the detonation polar, which is important in applications of oblique detonation in hypersonic propulsion systems, such as the oblique detonation engine. With the benefit of simplicity of the proposed theoretical method, it is easy to generate the detonation polar (coupled with chemical equilibrium) with high accuracy.
The detonation polar diagrams of stoichiometric hydrogenair mixture for different Mach numbers are shown in Fig. 12.Taking Ma = 10 as an example, the detonation polar is a closed curve and is divided into three segments by critical Points O, A and B. Point O is corresponding to the solution of normal detonation wave, θ = 0° and β = 90°. And Point B corresponds to the maximum wedge angle θfor the attached oblique detonation wave. For θ > θ, the detonation wave would be detached from the wedge, which is not favorable in applications.Divided by Points O and B,Segment OB is the strong shock solution, while Segment OAB is the weak shock solution. In nature, the weak shock solution is favored and usually occurs because the post-shock flow is supersonic.
Point A corresponds to the C-J oblique detonation wave with the normal-shock component of the post-shock Mach number Ma= 1, and hence the wedge angle for this point is denoted as θ. Then, shock solutions on Segment OA are the so-called under-driven oblique detonation waves since Ma> 1, while shock solutions on Segment AB are the socalled over-driven oblique detonation waves since Ma< 1.However, under-driven oblique detonation waves have not yet been observed in experiments, and some researchers considered they are abnormal in nature.As a result, only the over-driven oblique detonation waves are applicable in engineering.
From the above observation, the solution of a standing oblique detonation wave is on the Segment AB in the detonation polar,and hence the wedge angle must be θ<θ<θ.That is, the standing window of oblique detonation waves is enclosed by the θline and the θline, as shown in Fig. 13. For the Mach number 10 flow, it is 11.37°<θ<49.56°.With no doubt,the standing window will narrow down to zero with the decreasing Mach number, and no solution of standing oblique detonation waves exists below about Mach number 5.This indicates that the oblique detonation engine should work at high Mach numbers to gain a wide standing window for the stable operation of the system.Summarily, to precisely predict the standing window of oblique detonation wave in engineering design, it is necessary to use the shock relations coupled with chemical equilibrium.The importance of the theoretical work in this paper is clearly manifested.

Fig. 9 Convergence paths of proposed theoretical method compared with real chemical-kinetic process for solving normal shock problem (before shock: 0.42H2 + 0.21O2 + 0.79N2, T1 = 300 K, p1 = 1 atm, u1 = 2500 m/s).

Table 2 Comparison of flow parameters behind oblique detonation wave in hydrogen-air mixture (θ = 30°; before shock:0.42H2 + 0.21O2 + 0.79N2, T1 = 300 K, p1 = 0.4 atm, u1 = 3270 m/s).
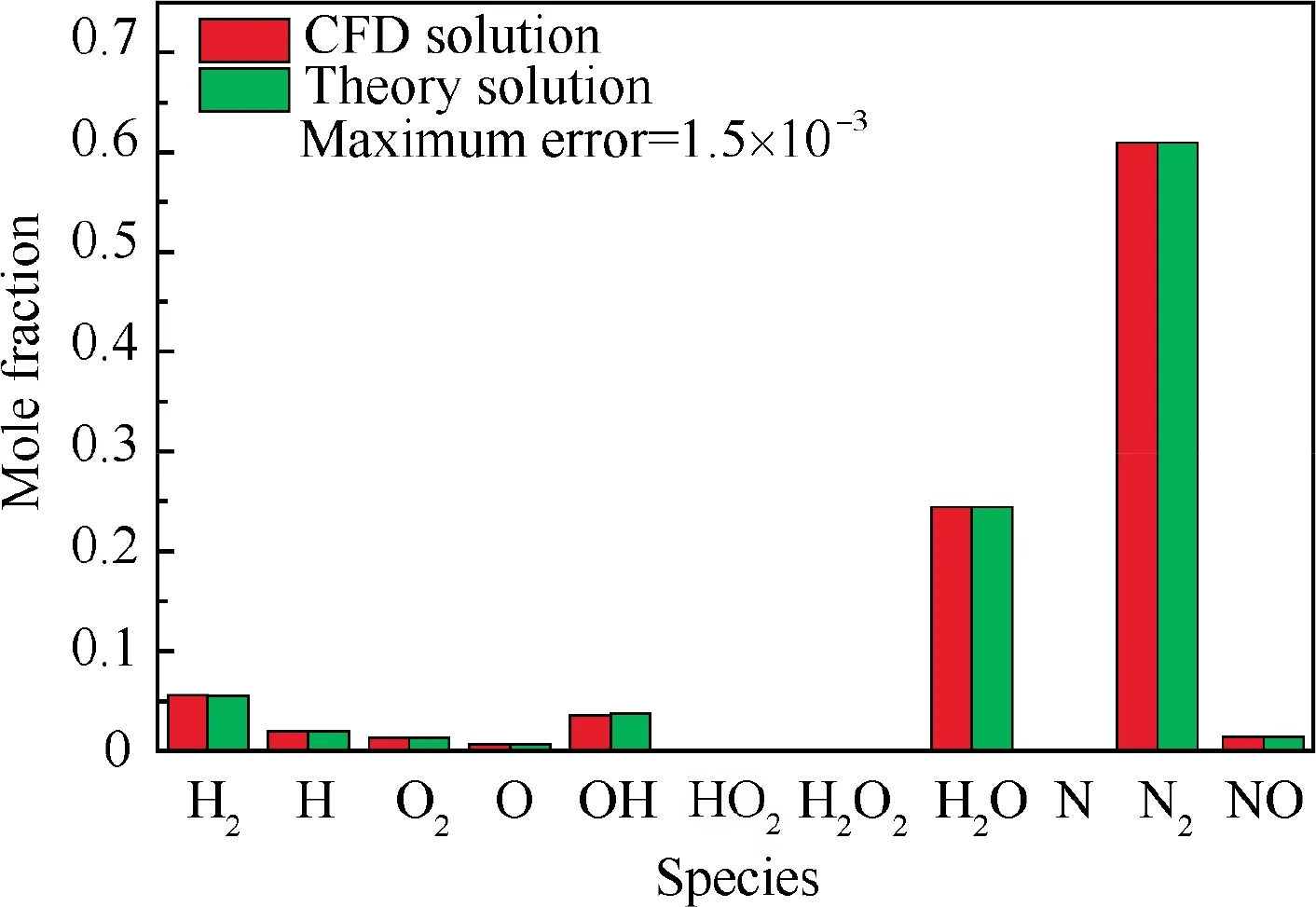
Fig. 10 Comparison of species compositions behind oblique detonation wave in hydrogen-air mixture (θ = 30°; before shock:0.42H2 + 0.21O2 + 0.79N2, T1 = 300 K, p1 = 0.4 atm,u1 = 3270 m/s).
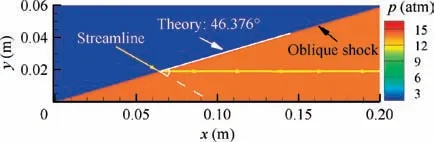
Fig. 11 CFD pressure contours of oblique detonation wave in hydrogen-airmixture(θ=30°;beforeshock:0.42H2 + 0.21O2 + 0.79N2, T1 = 300 K, p1 = 0.4 atm,u1 = 3270 m/s).

Fig. 12 Detonation polar diagrams of stoichiometric hydrogenair mixture (T1 = 300 K, p1 = 1 atm).
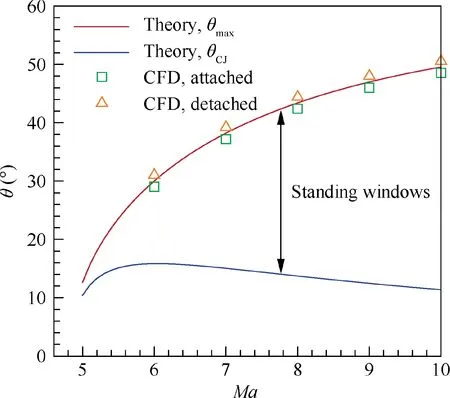
Fig. 13 Standing window of oblique detonation wave in a stoichiometric hydrogen-air mixture (T1 = 300 K, p1 = 1 atm).
Obviously, the accuracy in predicting the maximum wedge angle θis important to determine the width of the standing window of oblique detonation waves, since it changes significantly with Mach number (Fig. 13). To further validate the accuracy of the proposed theoretical method in predicting θ, numerical simulations are conducted near the theoretically predicted θ(±1°) to determine the specific flow patterns (attached or detached) of oblique detonation waves at different Mach numbers, and are summarized in Fig. 13. An example of the flow fields of oblique detonation waves near θ= 38.22° at Ma = 7 is shown in Fig. 14. As indicated in Figs.13 and 14,the predictions of θby CFD and the proposed theoretical method are in good agreement.
3.2. Stand-off distance prediction for detonation wave
When a sphere is placed in a supersonic flow, a bow shock is formed before the sphere,and the distance between the shock and the sphere along the stagnation streamline is so called the stand-off distance Δ, as shown in Fig. 15. It is one of the important design parameters in supersonic vehicles,especially the hypersonic vehicles. Moreover, it is often used as one parameter to validate numerical methods, especially in high-enthalpy dissociating air.As the same phenomena occur in detonation waves, the detonation stand-off distance is of the same importance. Limited by experimental facilities and measurement instruments,the experimental determination of detonation stand-off distance is difficult and large errors are generally encountered. In this paper, with the help of the proposed method to solve detonation wave coupled with chemical equilibrium,the theoretical predictions of detonation stand-off distance with high accuracy may become possible.
Fig. 15 Schematic of stagnation flow.
A well-known relation of the shock stand-off distance for a non-reactive air flow is given by Lobb,

Assuming that Eq. (38) is also satisfied in the theoretical prediction of detonation stand-off distance. Then, by given the sphere diameter D, the detonation stand-off distance Δ is only determined by the parameter ρ/ρof the equilibrium detonation wave that can be easily calculated by the proposed method in this paper.
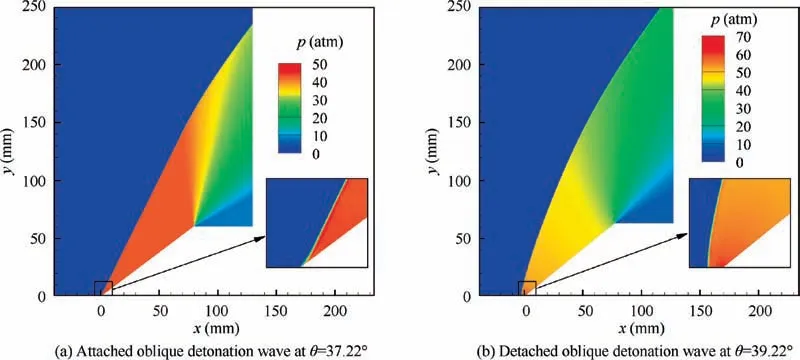
Fig. 14 Flow fields of oblique detonation waves in a stoichiometric hydrogen-air mixture of Ma = 7 (the predicted θmax in Fig. 13 is 38.22°).
Fig. 16 shows detonation stand-off distances predicted by the proposed method for a D = 10 cm sphere placed in the high-speed stoichiometric hydrogen-air mixture.It can be seen that the stand-off distance Δ decreases exponentially as Mach number increases for different freestream temperature T.And it decreases with the increasing of T.There exists a limit value of Δ at Δ/D = 0.04, if continually increasing the Mach number. With Eq. (38), it is obviously a result of the existence of limit value of ρ/ρacross detonation waves. The ‘‘Mach number independence” is achieved.Therefore, the difference of Δ with varying Tat high Mach number would be smaller than that at low Mach number, which is clearly shown in Fig. 16(b).
In order to validate the theoretical predictions of the detonation stand-off distances, numerical simulations are carried out, using our in-house CE/SE code, to provide the so called‘‘exact”values.Fig.17 shows an example of the simulated detonation flow field around a 10 cm sphere. The measurement values of the detonation stand-off distances at different Mach numbers and freestream temperatures in the simulated flow fields are summarized and shown in Fig.16.It can be seen that the theoretical predictions of the detonation stand-off distances agree well with the simulated ones in CFD, and the maximum relative error is about 4.5%. The proposed theoretical method shows good accuracy in predictions of equilibrium detonation stand-off distances.
It should be note that detonation waves are always characterized by characteristic lengths of chemical reactions. When the Mach number and freestream temperature are relatively low, which would result in a relatively long reaction zone, or the diameter of the sphere is relatively small,which would lead to a relatively short detonation stand-off distance, the flow between the leading shock front and the sphere surface may not reach the fully chemical equilibrium state and hence Eq.(38) may cause a relatively large error. Under such nonequilibrium occasions, a characteristic chemical reaction rate parameter should be introduced, and the coefficient in Eq.(38)is no longer a constant of 0.41 but a function of this characteristic chemical reaction rate parameter.
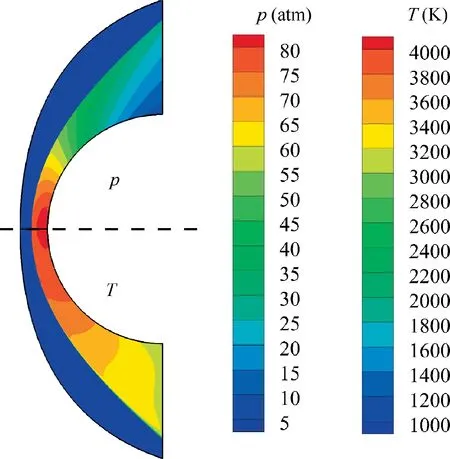
Fig. 17 Pressure and temperature contours of detonation flow fieldarounda10cmsphere(freestream:0.42H2 + 0.21O2 + 0.79N2, T1 = 300 K, p1 = 1 atm, Ma = 8).
3.3. Transition criteria of shock reflection in dissociated air
Steady shock reflections include regular reflection and Mach reflection,as shown in Fig. 18, where θ and Ma are the wedge angle and freestream Mach number, respectively. The regular reflection flow field (Fig. 18(a)) consists of an incident shock and a reflected shock, while the Mach reflection flow field (Fig. 18(b)) consists of an incident shock, a reflected shock,a Mach stem and a slip line, and these four discontinuities intersect at the so-called triple point.Shock polar analysis is a simple and effective tool in theoretical studies of shock reflection phenomena.As shown in Fig. 19, Mach reflection occurs at θ > θ, while regular reflection occurs at θ<θ,where θand θare the so-called von Neumann criterion for Mach reflection transiting to regular reflection and detachment criterion for regular reflection transiting to Mach reflection, respectively. At high Mach numbers, θand θare not equal and θis greater than θ. At θ< θ < θ, both regular reflection and Mach reflection can exist, resulting in hysteresis in shock reflection transition.Studies of shock reflection phenomena and their transition are not only conducive in understanding the supersonic flow physics, but also have a great importance in engineering applications.

Fig.16 Detonation stand-off distance as a function of Mach number and freestream temperature T1 for a D=10 cm sphere placed in high-speed stoichiometric hydrogen-air mixture (p1 = 1 atm).

Fig. 18 Steady shock reflections.
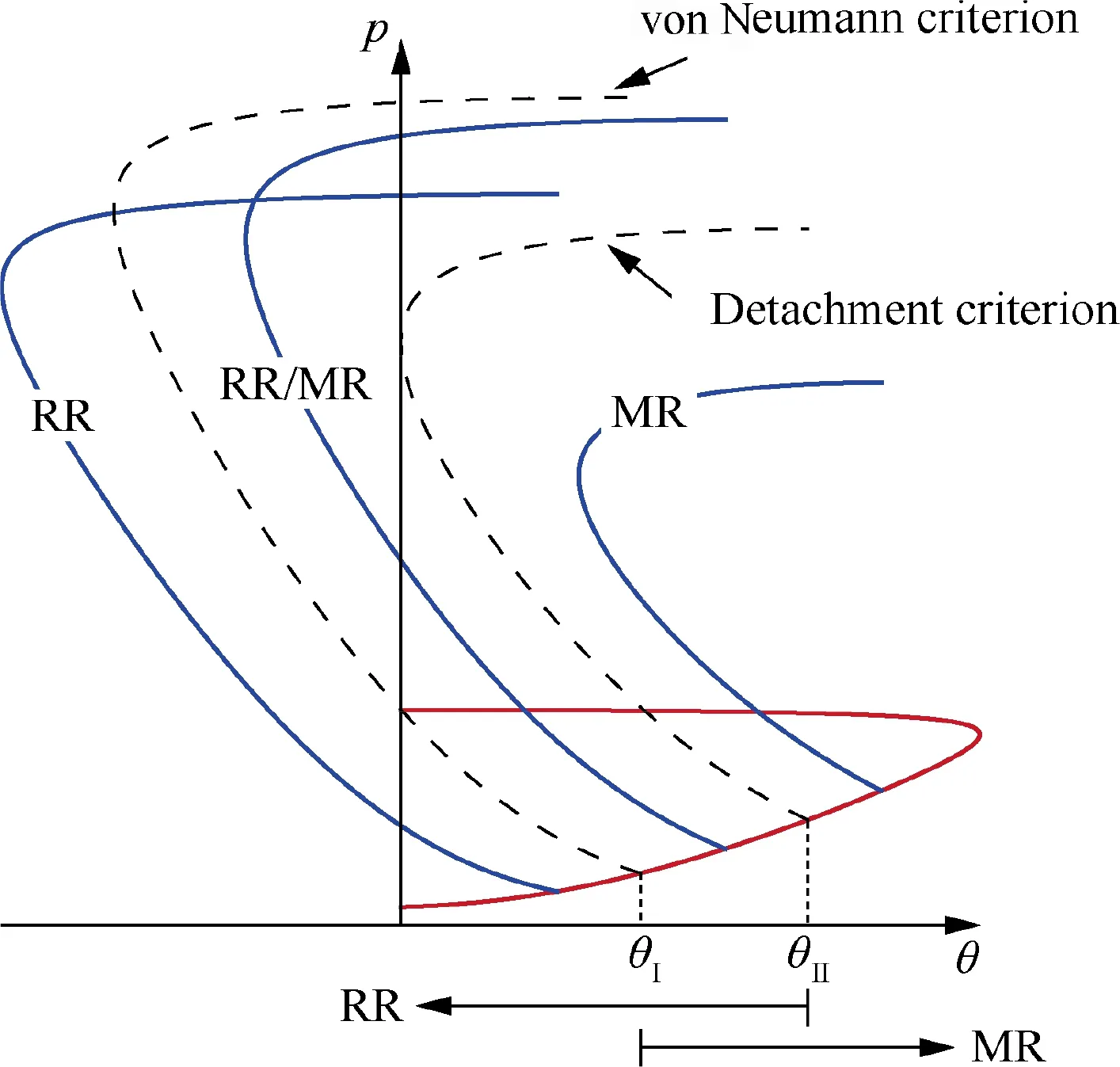
Fig. 19 Shock polars of Regular Reflection (RR) and Mach Reflection (MR) and their transition criteria.
As for hypersonic flows, oxygen and nitrogen molecules in air will be dissociated into atoms or recombined into oxynitrides in the high-temperature environment behind a strong shock wave. Hence, the shock relation in dissociated air will be quite different from that of the frozen flow due to the change of mixture compositions and physical properties across the shock and the accompanying thermal effects of chemical reactions, resulting in discrepancy in shock reflection transition criterion predictions. With the proposed theoretical method in this paper, the chemical-equilibrium oblique shock solutions of multiple reflections with high accuracy can be obtained readily and the chemical-equilibrium shock polars for determining the transition criteria of shock reflections similar to Fig. 19 can be generated accordingly. In this section, 6 species (N, O, Ar, NO, N and O) are considered for the air dissociation,and the undissociated freestream air is composed of 0.78 N+ 0.21O+ 0.01Ar. Flow parameters in the freestream are T= 226.51 K and p= 1197 Pa, which correspond to the static temperature and pressure of hypersonic flight in the atmosphere at an altitude of 30 km.
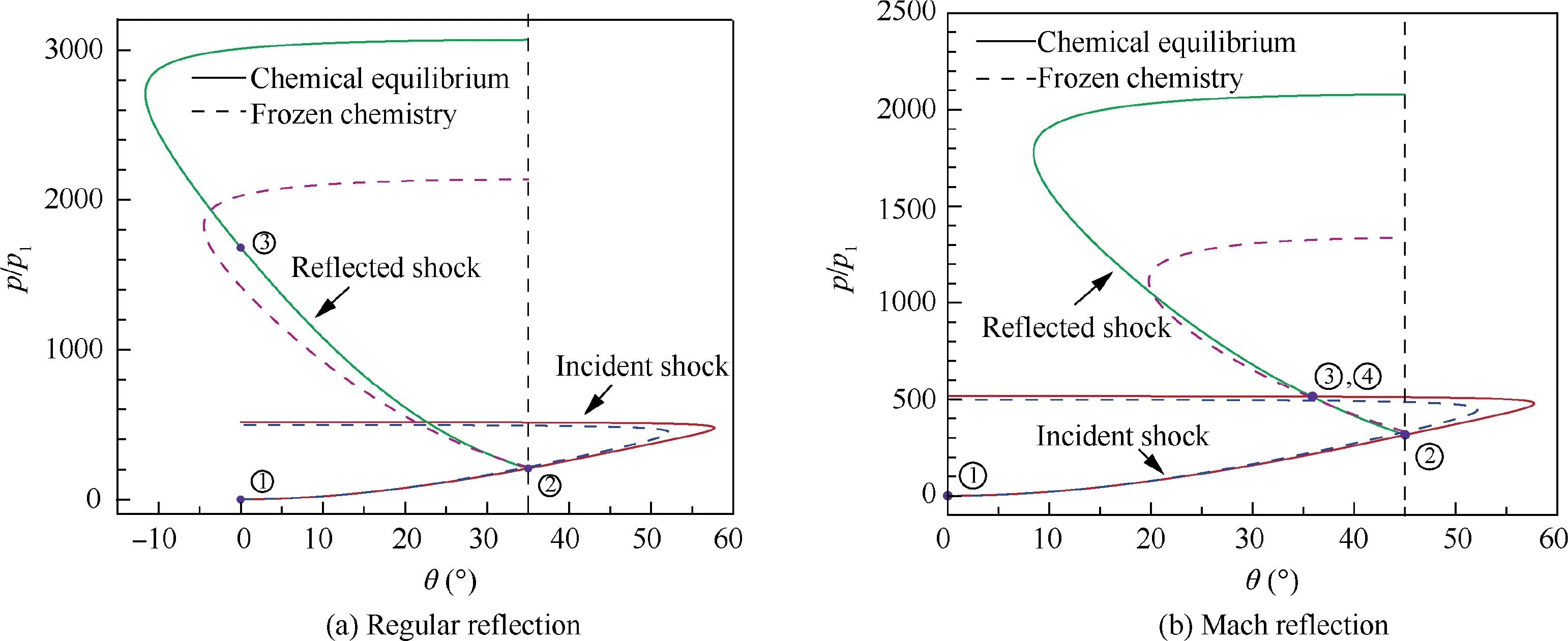
Fig. 20 Shock polar analyses of regular reflection and Mach reflection (freestream: 0.78N2 + 0.21O2 + 0.01Ar, T1 = 226.51 K,p1 = 1197 Pa, Ma = 20).
The incident shock polar and reflected shock polar in dissociated air for Ma = 20 and θ = 35° or 45°, corresponding to the regular reflection or Mach reflection,are shown in Fig.20.Shock polars with frozen chemistry are also available in Fig. 20 for comparisons. In addition, as an example, mixture compositions across the incident and reflected shock waves in the regular reflection of Fig. 20(a) are compared in Fig. 21.Notably,since Eqs.(1)-(3)are used to evaluate the thermodynamic properties of each species, vibrational equilibrium has been already considered in both frozen and dissociated cases,and the differences between them only arise from the inclusion of dissociated reactions of air. It can be revealed that, due to the existence of dissociation and recombination reactions in the dissociated air, shock polar profiles are greater than those with frozen chemistry. Consequently, the value of maximum wedge angle that is related to the detachment criterion of shock reflection increases. Moreover, shock polar profiles between the equilibrium and frozen cases are more differentiable in reflected shocks. In summary, the transition criteria of shock reflection in the equilibrium dissociated air are expected to be very different from those predicted by frozen chemistry.
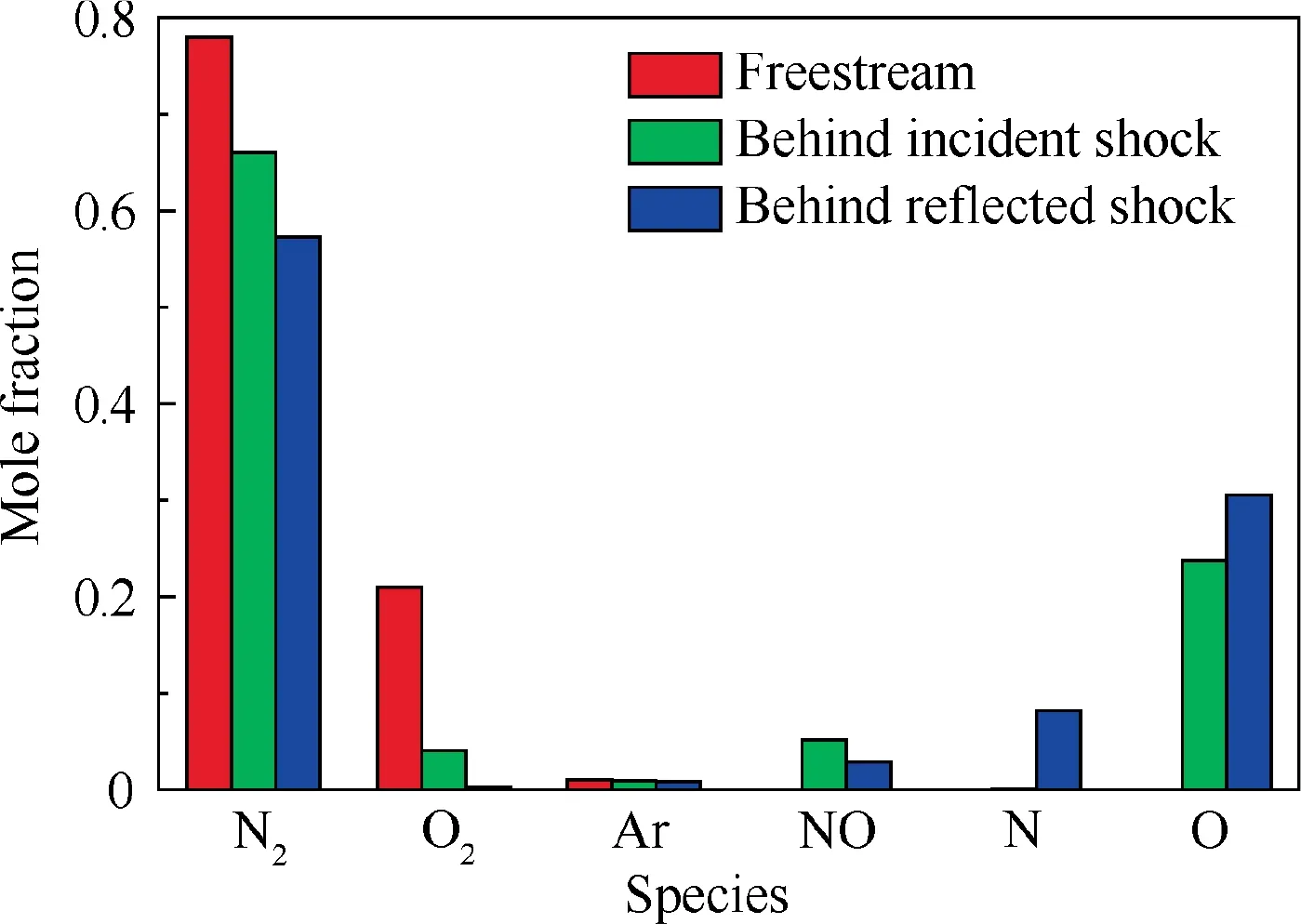
Fig. 21 Compositions of air in regular reflection case in Fig. 20(a).

Fig.22 Transition criteria between Regular Reflection(RR)and Mach Reflection (MR).
Fig. 22 shows the predicted transition wedge angles as a function of Ma between regular reflections and Mach reflections coupled with chemical equilibrium, comparing with the predicted values by frozen chemistry. It can be seen that at low Mach number where chemical reactions do not occur in air, frozen chemistry predicts the same values of transition wedge angle with chemical equilibrium. However, with the increasing of Mach number,effect of air dissociation on shock reflection and hence difference of transition wedge angles predicted by chemical equilibrium and frozen chemistry begin to emerge at about Ma = 6. Both transition criteria (i.e., von Neumann criterion and detachment criterion) are underpredicted when shock relations with frozen chemistry are used at Ma > 6, particular in the prediction of detachment criterion. Taking Ma = 20 as an example, the predicted wedge angles of von Neumann criterion by chemical equilibrium and frozen chemistry are θ= 19.05°and 18.53°, respectively,and the prediction by frozen chemistry is only 2.7%lower than that by equilibrium counterpart. Comparatively, they are respectively θ= 41.20° and 37.21° for the detachment criterion and the under-prediction of frozen chemistry increases to 9.6%. Therefore, the shock relation coupled with chemical equilibrium must be used at high Mach number to obtain accurate prediction of shock reflection regimes. The importance of this work is again manifested.
4. Conclusions
Reactive shock waves are common in nature and engineering applications. Fast predictions of reactive shock waves via theoretical solutions are of great importance in the understanding of supersonic flows and engineering preliminary designs. In this study, a theoretical method is proposed to solve shock relations coupled with chemical equilibrium. Some conclusive remarks are summarized as follows:
(1) The proposed method can be used in various reactive shock waves, including detonation waves in combustive mixtures, shock waves in dissociated air, etc. To ensure good stability and fast convergence, the global iterative solving process is specially designed to follow a virtual physical and chemical process mimicking the ZND process in reactive shock waves.The global iterative process is implemented through alternatively solving the shock relations with known compositions and the chemical equilibrium compositions at a specific temperature and pressure from the compressive states of non-reactive shocks. The shock relations with known compositions are solved using the derived single-variable Newton iteration formulas rather than the conventional multidimensional Newton method to reduce the complexity of the problems. Additionally, the equilibrium compositions at a specific temperature and pressure are solved via the classic minimization of free energy method of NASA.
(2) Comparisons of the normal detonation wave solution with the exact ZND solution and the oblique detonation wave solution with numerical simulation results are used to validate the convergence and accuracy of the proposed method. It is demonstrated that the convergent process is stable and very close to the real chemicalkinetic process. High accuracy is achieved as well.
(3) Based on this theoretical method, serval applications have been demonstrated, including calculations of detonation polar and standing windows for oblique detonations, standing-off distance predictions for bow detonation waves, and predictions of transition criteria of shock reflection in dissociated air.Significant discrepancies of the predicted results between chemical equilibrium and frozen chemistry have been revealed, which shows the great importance of using chemical equilibrium in theoretically predictions of reactive shock waves with high accuracy.
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
This study was co-supported by the National Natural Science Foundation of China (Nos. 11672312, 11772284 and 11532014), the Research Grants Council, Hong Kong, China(No. 152151/16E) and the Department of Mechanical Engineering, The Hong Kong Polytechnic University, China (No.G-YBYJ).
Appendix A.
The detailed equations for calculating the one-dimensional ZND solution of the steady reactive normal shock are given as follows. Assume that the shock front is located at x = 0,and the high-speed reactive mixture flows from left (x < 0)to right (x > 0). Therefore, the ZND profile of the reactive normal shock starts from x =0.As for x<0,it is the freestream state before the shock. The one-dimensional steady reactive Euler equation governing the flow within the ZND profile(x ≥0) is

In Eq.(A2),the specific enthalpy of the mixture h is a function of the temperature T and chemical compositions Y(i=1,2,...,n)of the mixture.Recalling the equation of state of the mixture (Eq. (11)), the density of mixture ρ can be calculated from p, T and Y. Hence, F is a function of the parameter set of {p, T, u, Y}. On the other hand, the parameter set of{p,T,u,Y}can also be uniquely solved by a given F.The mass production rate of each species ˙ωin S can be calculated from the pressure p, temperature T and chemical compositions of mixture Yvia a specific chemical reaction mechanism. Therefore,S is a function of F,that is,S=f(F).Obviously,Eq.(A1)is an ordinary differential equation, with the initial value condition of

where the F values at the right-hand side can be calculated from the flow parameter set of {p, T, u, Y} right behind the corresponding frozen normal shock. Finally, Eqs. (A1) and(A3) compose an initial value problem for calculating the ZND solution, which can then be integrated explicitly via a Runge-Kutta method, such as the fourth-order scheme as below,
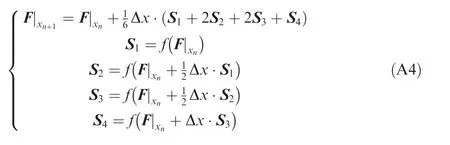
 Chinese Journal of Aeronautics2022年6期
Chinese Journal of Aeronautics2022年6期
- Chinese Journal of Aeronautics的其它文章
- Experimental investigation of a gliding discharge plasma jet igniter
- Evolution of turbulent boundary layer over a three-dimensional bump
- Conceptual design and preliminary experiment of icing risk management and protection system
- Direct thrust control for multivariable turbofan engine based on affine linear parameter-varying approach
- Characteristics of reattached boundary layer in shock wave and turbulent boundary layer interaction
- Structurally coupled characteristics of rotor blade using new rigid-flexible dynamic model based on geometrically exact formulation
