信号交叉口行人二次过街下右转车通行能力与延误估计模型

李冰，王正辉，马铭炜，杨鸿宇，冯悦

(昆明理工大学，交通工程学院，昆明 650500)

0 引言

对于行人过街需求大的交叉口，当红灯时间过长时，行人易闯红灯，因此，有必要研究如何减少行人等待延误的信号控制方法，其中，行人二次过街信号控制是常用的方法之一。例如，在多相位信号控制中，可以利用直左或专左相位的时空资源，增设行人过街相位，减少行人过街延误[1-2]。CHEN等[3]提出一种用于协调大型信号交叉口行人二次过街设置的行人和车辆信号相位的方法，减少行人二次过街设置对直行和左转车辆吞吐量的影响。SONG 等[4]设计一种新的行人二次过街模式，为行人过街提供额外的时间。YU 等[5]设计一种与两段式街区中人行横道有关的信号优化方案，以优化行人过街，减少行人延误。

大多数关于行人二次过街的研究集中在如何减少行人延误和提高行人满意度上，忽略了增加行人过街时间后对右转车的影响。然而，由于多数交叉口右转车流不受信号控制，在行人过街需求较大的交叉口，随着行人过街时间的增加，往往会加剧行人与右转车流的冲突[6]；此外，由于行人过街享有优先通行权，右转车只有等待行人过街流出现可穿插间隙时才能通行，所以，当右转车流量较大时，易发生由于行人过街时间增加导致右转车排队长度增大的现象，进而对同向直行车流造成干扰，加大进口道交通压力。以直左分开放行的典型四相位为例，在交叉口不设置行人二次过街时，右转车只会和来自人行横道两端的行人发生冲突；但在交叉口设置行人二次过街后，右转车不仅会和来自人行横道两端的行人发生冲突，还会和来自中央安全岛的行人发生冲突，具体情况将在第1节中以图例进行说明。在这种情况下，需要分析行人二次过街的设置对右转车的影响，并随着行人过街时间的增加，行人二次过街的设置对右转车通行能力和延误的影响在驾驶员的可接受范围内。因此，本文在利用可插车间隙理论分析右转车通行能力时，通过现场数据调查和分析，拟合行人群体与行人流量之间的关系，建立右转车通行能力模型和延误模型，考虑单向和双向行人流的影响与信号控制，同时考虑聚集到达和自由到达对右转车的影响。定量分析典型四相位下有行人二次过街和无行人二次过街的右转车通行能力和延误，为交通治理提供参考。

基于此，本文以行人过街影响下右转车的通行能力和延误为评价指标，以常规四相位对称放行的信号控制交叉口为例，建立行人二次过街设置标准，为行人二次过街信号控制的设置提供理论依据。

1 行人二次过街对右转车通行能力影响分析

为进一步分析行人二次过街与右转车流的冲突情况，如图1所示，在典型四相位下相位2与相位4 中的行人流为增设行人二次过街控制下的行人流；以右转车流R1为例，在没有设置行人二次过街的情况下，R1仅与行人流P2和P7发生冲突；当在交叉口设置行人二次过街后，R1在原有冲突的基础上增加了与行人流P3、P5、P9和P10的冲突。可以看出行人二次过街的设置将增大与右转车流的冲突概率，进而影响右转车通行能力。

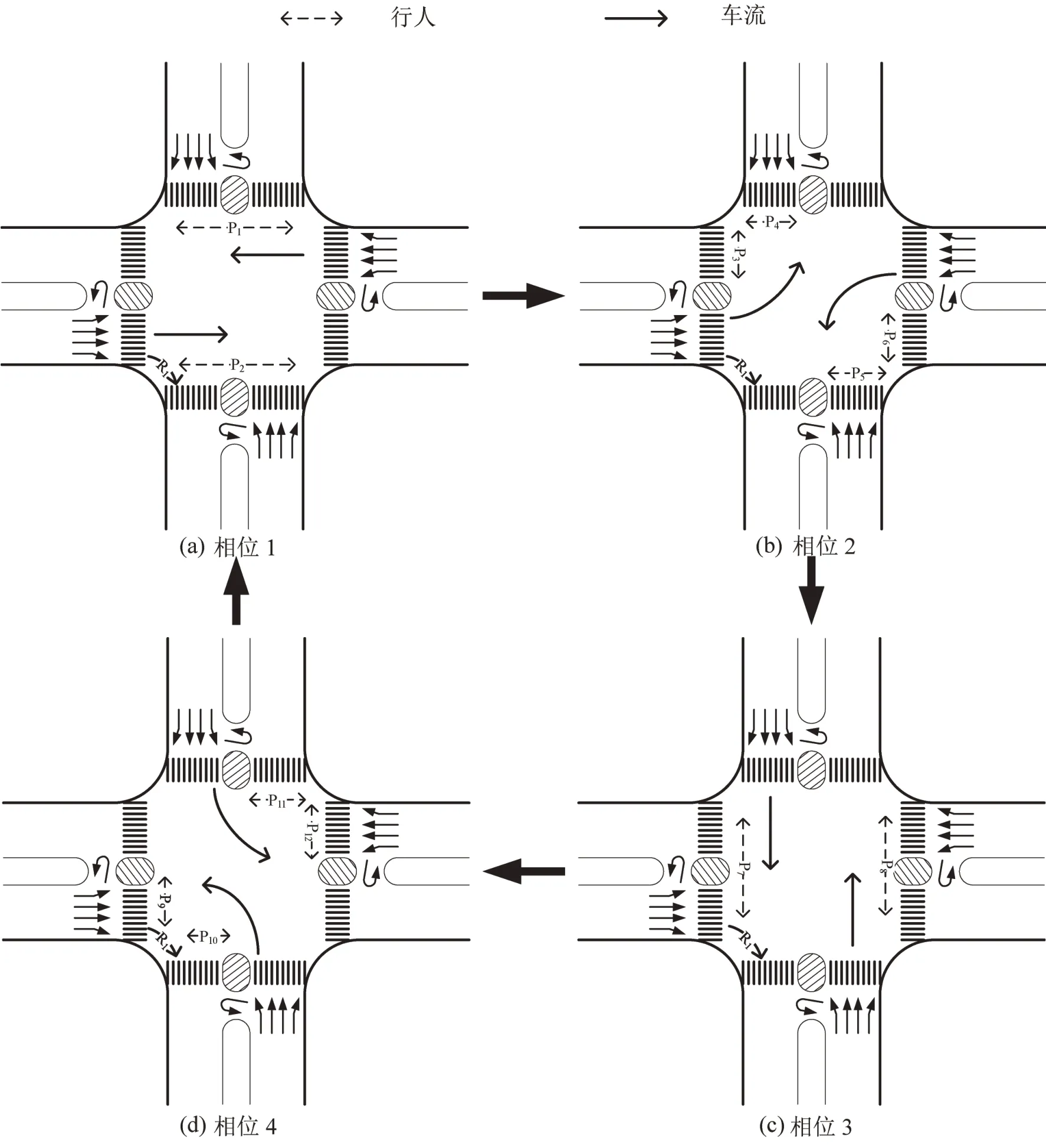
图1 典型四相位下的行人二次过街信号示意图Fig.1 Typical four-phase signal with pedestrian two-stage crossing

在分析行人过街对右转车通行能力影响时，还需考虑右转车道功能情况，如图2所示。

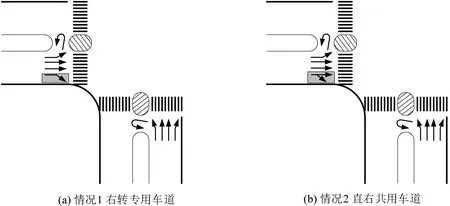
图2 右转车道的两种情况Fig.2 Two cases of functions of right-turn lane

当设置直右共用车道时，右转车流量较小，行人二次过街设置对其通行能力影响小，所以，本文仅研究右转专用道设置下的车辆通行能力。在该情况下，右转车与行人的冲突包括以下3方面。

1.1 与行人过街没有冲突

行人过街为红灯时，行人须在人行道上等待过街绿灯启亮时才能通行，此时，右转车通行能力为

式中：TRP为行人有效红灯时间；Tc为周期长度；Srs为右转车辆的饱和流率，为右转车饱和车头时距。

1.2 行人过街绿灯启亮初期行人集聚通过时与右转车的冲突

当行人绿灯启亮时，行人占据冲突区，此时，右转车只有等集聚到达的行人通过冲突区，且后续到达行人群出现可穿插间隙时，方可通行。在该种情况下，右转车通行能力CR2=0。此时的关键在于确定行人集聚通过时占据冲突区的时间，如图3所示。

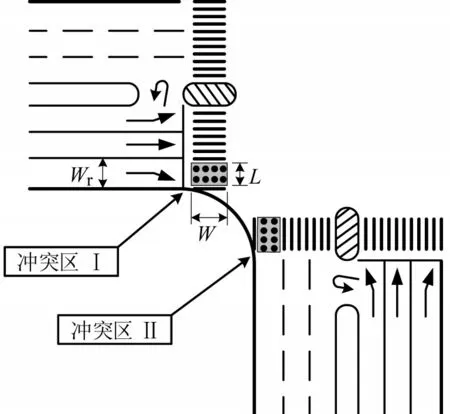
图3 行人与右转车辆的冲突区域Fig.3 Conflict zones between pedestrians and right-turn vehicles

此时，将聚集过街的行人看作是一个行人体，其在道路上的投影面积S=LW，L和W分别为行人体的长度和宽度，本文中W为人行横道宽度。S和W分别为

由式(2)和式(3)可得

式中：λP为行人流量；TR为行人红灯时间；kP为行人经过冲突区域的人均占地面积(根据场景分析取值，本文取1.8 m2·人-1)。

由于行人聚集过街后还需通过右转车道宽度Wr，所以，行人集聚通过时占据冲突区的时间TL可确定为

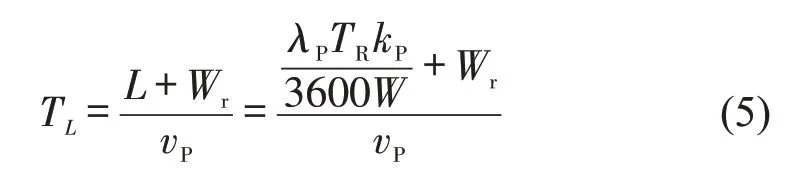
式中：vP为行人过街速度，本文取1.2 m·s-1。由于行人过街方向的不同，其密度也会有所差别，对于从近端(邻近右转车道的人行道)进入人行横道的行人流添加下标A；从远端(远离右转车道的人行道)进入人行横道的行人流添加下标B，不同方向行人密度值需根据实际调查所得。典型四相位行人二次过街如图4所示。

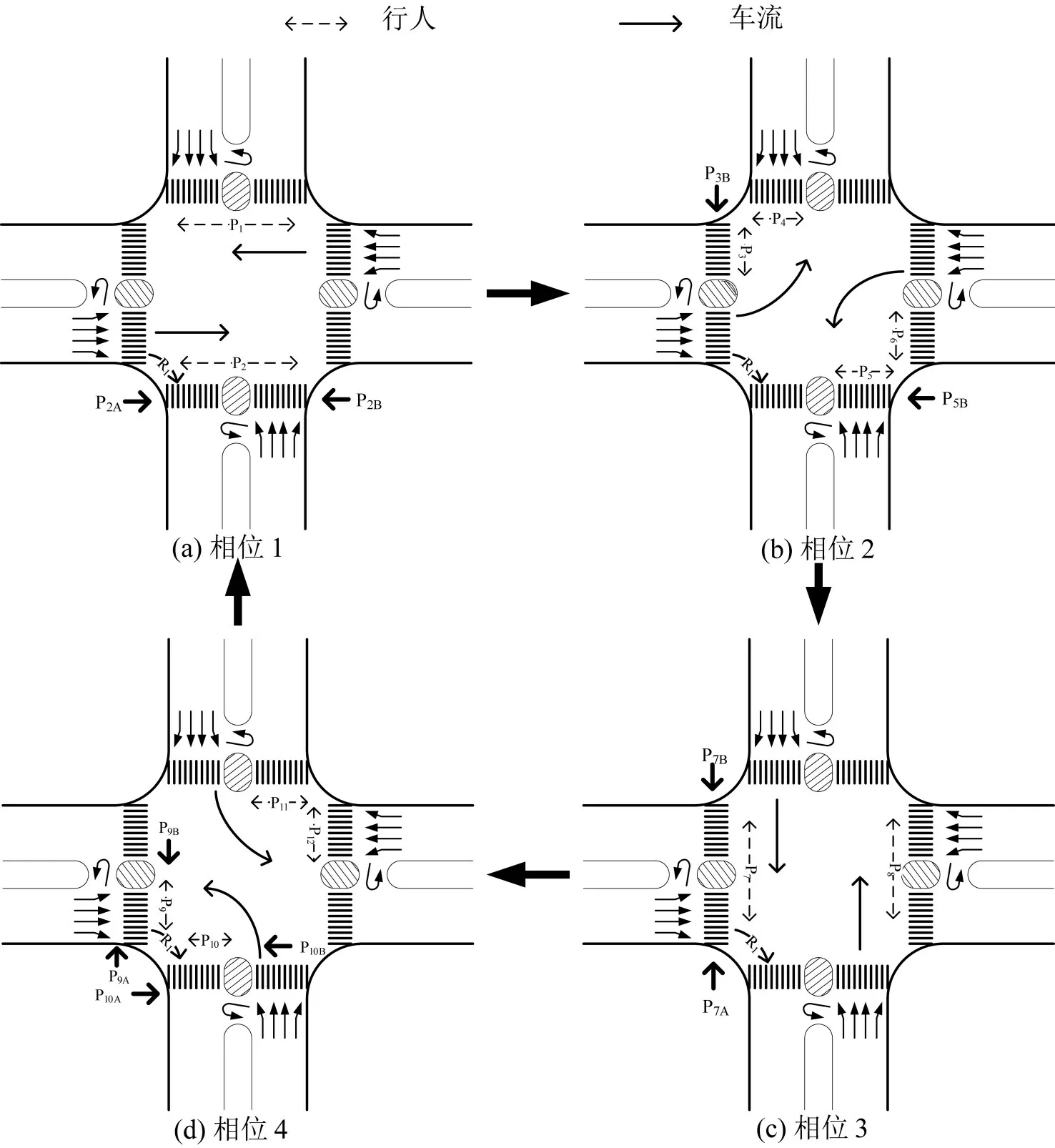
图4 典型四相位下的行人二次过街近端与远端行人流示意Fig.4 Near-side and far-side pedestrian flow diagram in typical four-phase signal with pedestrian two-stage crossing

1.3 行人自由到达冲突区时与右转车的冲突

对于自由到达冲突区的行人，假设到达人行横道处的行人时间差在1 s 以内的为同一群体，根据研究表明[7]，当行人流量适中时，行人群的到达时距Hp服从负指数分布，其概率密度函数为

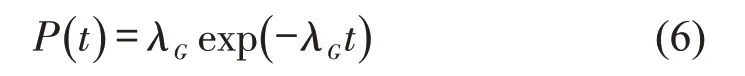
式中：λG为平均行人群体数量；t为时间变量。

通过对昆明市10个行人过街观测点持续1 h数据进行回归分析可得：当行人流量为p时，平均每群中的人数、平均行人群体数量及平均到达时距为

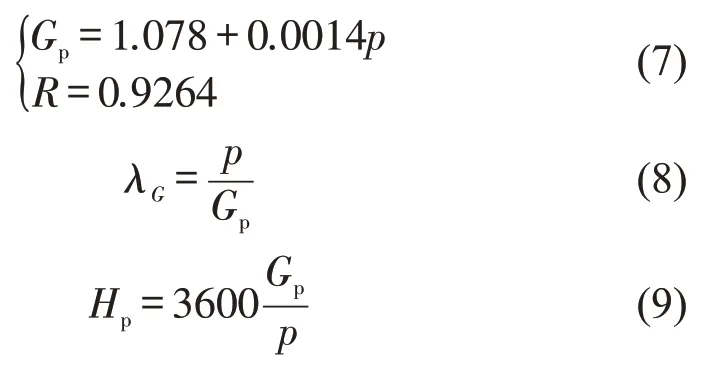
式中：Gp为行人群体的平均人数；R为相关系数。

当行人在绿灯期间自由通过人行横道时，此时，右转车只有在行人流出现可插车间隙时才能通过冲突区，当右转车通过单向行人流时，行人群体时距tPA和tPB，只需满足tcr≤tPA或tcr≤tPB；当右转车需同时通过双向行人流时，需满足tcr≤tPA∩tcr≤tPB，tcr为右转机动车的临界可穿越间隙。基于此，本文以可插车间隙理论为依据，并借用文献[8]的分析方法，计算该冲突下的右转车通行能力。

设右转机动车的车道可容纳无穷辆车排队，设tc为行人流中允许右转机动车穿越的最小车头时距，即临界间隙。对于任意大于tc的t及微小增量Δt，Hp在[t,t+Δt] 范围内的概率为Δtp(t)，一个周期内Hp在该范围内出现的次数为CλGΔtp(t)，C为信号周期时长。把Hp分割成tc与trs之和，通过推导可知：Hp可让右转机动车流穿越的车数为，所以，一个周期内在[t,t+Δt]内的那些Hp可让右转机动车流穿越的车辆数为

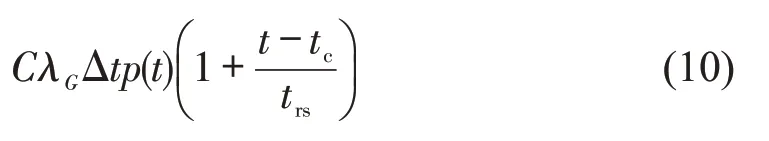
令Δt→0，并对式(10)求积分，可得

表1 行人过街特征数据采集(观测时段7:00-18:00)Table 1 Data collection of pedestrian crossing characteristics(observation period is 8:00-18:00)

前文已假设右转机动车的车道可容纳无穷辆车排队，因此，此时右转车流车道长度折减率可认为等于1，将负指数分布的概率密度函数代入式(11)，得

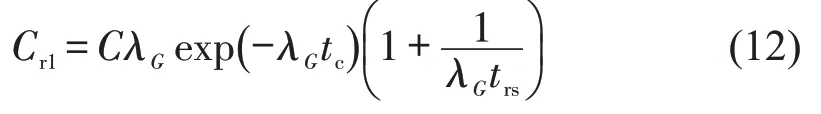
式中：Cr为右转车流通过自由到达的单向行人流时的通行能力值，当行人流双向通行时，需同时考虑行人群体的到达时距分布，假设不同方向通行的行人流为两个独立发生的事件，此时，双向行人流到达时距的概率密度为

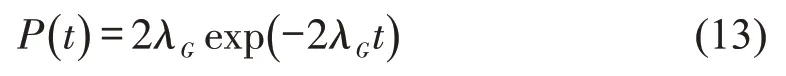
将式(13)代入式(11)可得右转车穿越双向行人流时的通行能力为

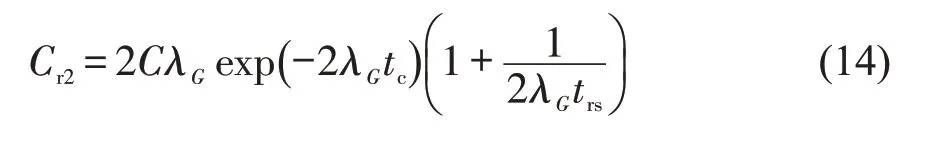
2 行人二次过街设置下的右转车通行能力计算

2.1 相位1放行时右转车通行能力

如图4所示，相位1放行时，与右转车冲突的行人流为P2，只需考虑P2A(聚集到达含于P10)自由到达时对右转车的影响；P2B需同时考虑行人集聚与自由到达对R1的影响。综上，相位1 放行时R1的通行能力为

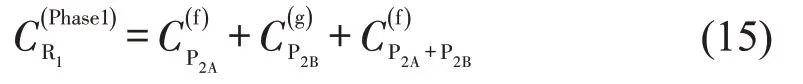
式中：为P2A自由到达时R1的通行能力；为P2B集聚到达时R1的通行能力；为P2A、P2B同时自由到达时R1的通行能力。

2.2 相位2放行时右转车通行能力

如图4所示，此时无行人流与R1发生冲突，R1的通行能力为饱和流率，即

式中：为行人流P5的绿灯时长。

2.3 相位3放行时右转车通行能力

从图4可以看出，相位3放行时，与右转车冲突的为P7，而P7中又包含P3对右转车的影响；对于远端方向的P7B而言，P3中已经包含了聚集通过时的影响，因此，只需考虑P7B自由到达对右转车的影响；对于近端方向的P7A而言，需同时考虑行人集聚与自由到达对R1的影响。综上，相位3 放行时R1的通行能力为

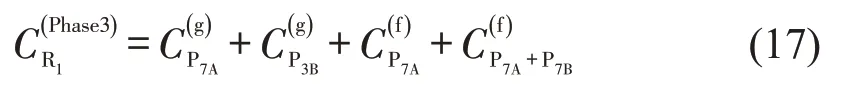
2.4 相位4放行时右转车通行能力

如图4所示，相位4放行时，与右转车冲突的行人流为P9和P10，因此，本文取右转车穿越P9和P10的最小值为该相位右转车通行能力。由于P9是紧接着P7放行的，故此时只考虑P9自由到达时对右转车的影响；而对于P10而言，远端方向P10B由相位2 放行时P5聚集至驻足岛的行人构成，所以，需考虑P10B集聚到达对右转车的影响；近端方向P10A需同时考虑行人集聚与自由到达对右转车流的影响。综上，相位4放行时R1的通行能力为

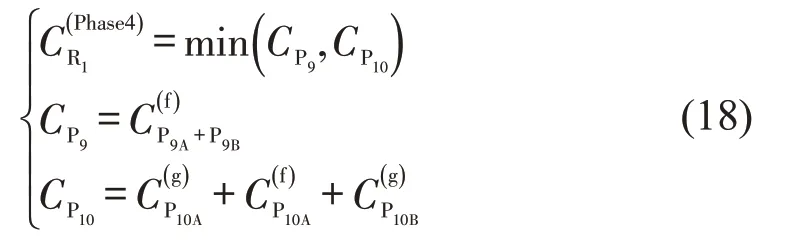
3 行人二次过街未设置下的右转车通行能力计算

行人二次过街未设置时，与R1冲突的行人流为相位1 的P2和相位3 的P7。无行人二次过街如图5所示。

3.1 相位1放行时右转车通行能力

如图5所示，相位1 放行时，对于P2A与P2B而言，需同时考虑行人集聚与自由到达对R1的影响。综上，按照行人通行顺序，相位1 放行时R1的通行能力为

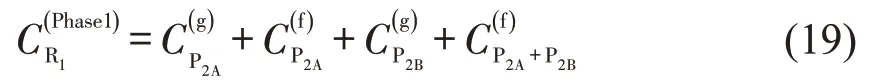
式中：为P2A集聚到达时R1的通行能力；为P2A自由到达时R1的通行能力；为P2B集聚到达时R1的通行能力；为P2A和P2B同时自由到达时R1的通行能力。

3.2 相位2和相位4放行时右转车通行能力

如图5所示，当相位2和相位4放行时，没有行人流与R1发生冲突，通行能力为右转车流的饱和流率，即

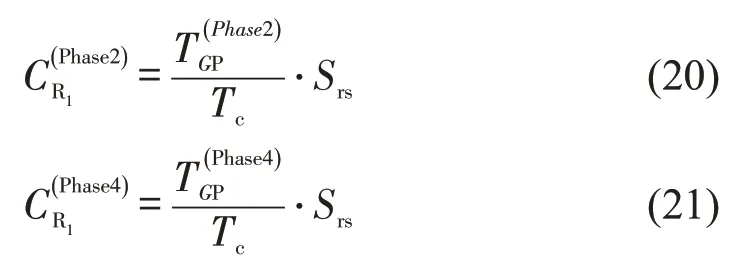
式中：、分别为相位2、相位4行人流的绿灯时长。

3.3 相位3放行时右转车通行能力

如图5所示，相位1 放行时，对于近端方向P7A与远端方向P7B而言，均需同时考虑行人集聚与自由到达对R1的影响。综上，相位3 放行时R1的通行能力为

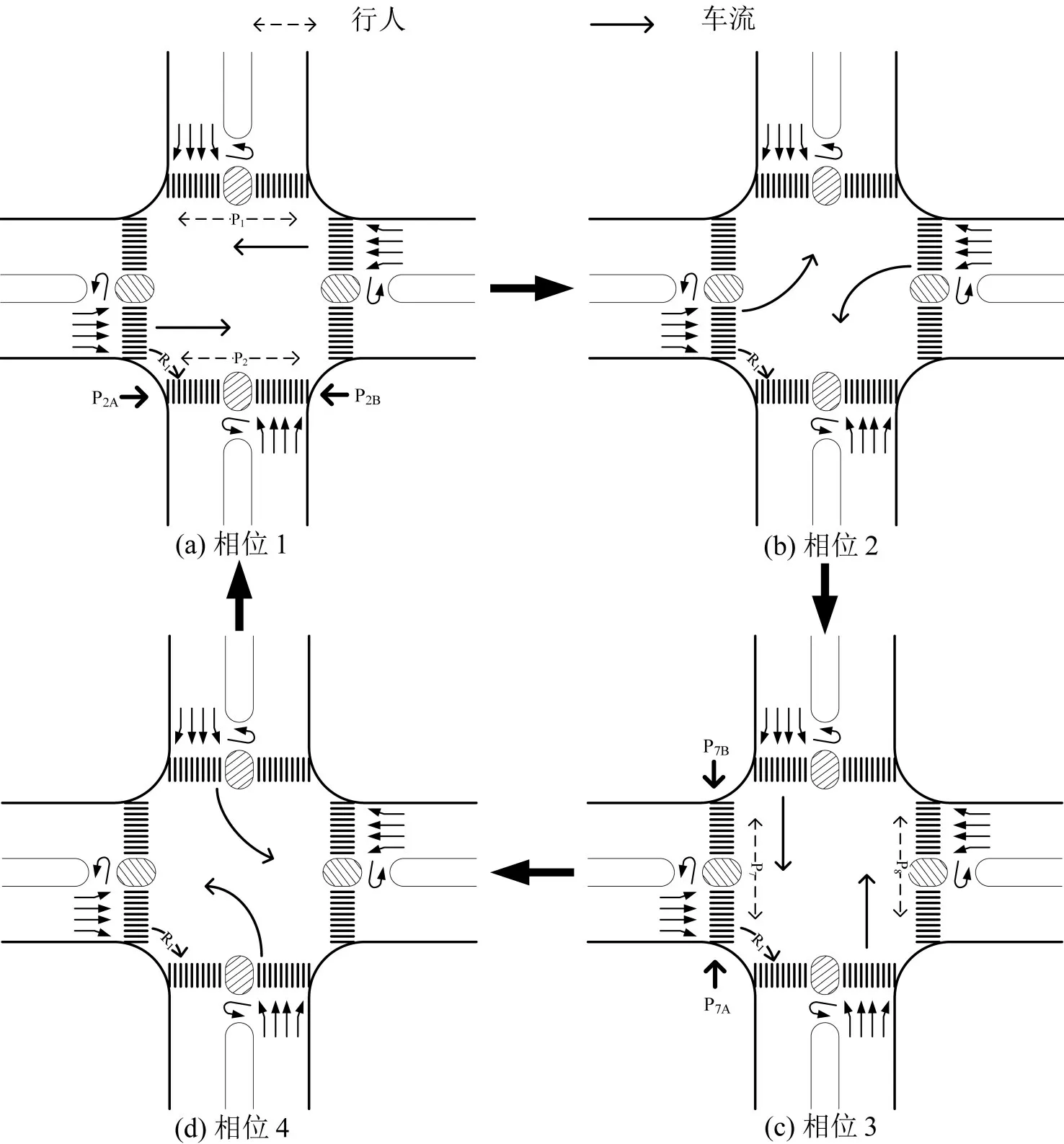
图5 典型四相位下的无行人二次过街近端与远端行人流示意Fig.5 Near-side and far-side pedestrian flow diagram in typical four-phase signal with pedestrian one time crossing

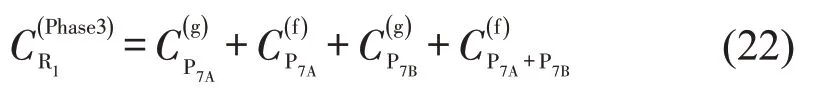
4 行人与右转车延误分析比较

4.1 行人延误分析

信号交叉口行人延误除了红灯等待产生的延误外，还存在绿灯时与右转车冲突时的附加延误[9]。本文假设当行人与右转车冲突时，行人享有优先通行权，行人延误可忽略不计，因此，信号交叉口行人延误即为行人红灯等待产生的延误。行人延误采用Webster延误公式计算，即

式中：dp为行人延误；C为周期时长；Tpg为行人绿灯时间。

4.2 右转车延误分析

由于大多数交叉口右转车均不受信号控制，因此，右转车延误主要来自于行人过街干扰时的延误[10]。如上述，根据行人流的不同消散形式，本文将右转车延误模型分为两部分：

(1)行人集中到达时对右转车的延误，右转车只能寻找可穿越间隔通过，此时，车辆的延误时间等于行人消散所占据冲突区时间，记为D(r1)，利用式(23)计算。

(2)行人随机到达时对右转车的延误，此时，右转可以选择可穿越间隙通过交叉口。车辆延误等于车辆到达时刻与车辆离开时刻之差。

本文借鉴韩印等[11]的分析思路构建右转车延误模型，定义以下变量：随机变量θ为车辆到达冲突点处的时刻，其值为行人随机消散过程结束时刻与车辆到达时刻之差；θ的概率密度为g(θ)，对应的概率分布为G(θ)，本文设到达时刻为均匀分布；随机变量dr为车辆的延误，在该部分延误的条件下0≤dr≤Te(Te为行人相位绿灯结束时刻)；dr的概率密度为fr(dr)，对应的概率分布为Fr(dr)。

车辆在θ时刻到达，等待可穿越间隙，当第1个可穿越间隙出现时，车辆离开，此时，产生延误dr，根据泊松过程的剩余寿命定理和可穿越间隙服从泊松分布假设，得到可穿越间隔的剩余寿命，此时延误的分布同指数分布，即

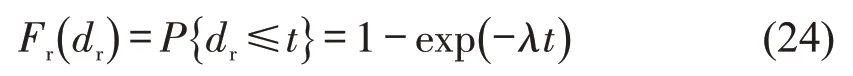
式中：λ为可穿越间隙的强度。

延误dr的概率密度为

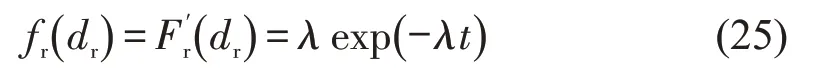
由于车辆到达具有一定的随机性，在车辆于θ时刻到达的条件下，其延误的分析函数为Fr(dr,θ)，对应的概率密度为fr(dr,θ)。

当0≤dr＜θ时，右转车辆发现可穿越间隙即可离开，这时候的分布函数为Fr(dr,θ)=Fr(dr)；当dr≥θ时，车辆只能等待行人流消散后离开，这时dr=θ，其分布函数Fr(dr,θ)=1-F(θ)，F(θ)为θ的分布函数，故延误dr的分布函数为

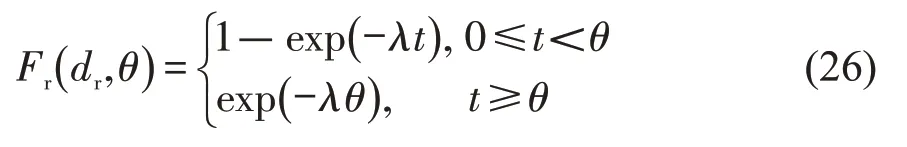
行人随机消散的时间区间为[0,Te]，在[0,Te]内右转车辆在到达时刻为θ的条件下的平均延误为

将式(28)展开，即

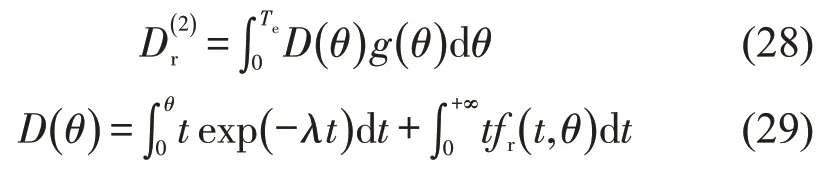
将dr=θ代入式(29)的第2部分可得

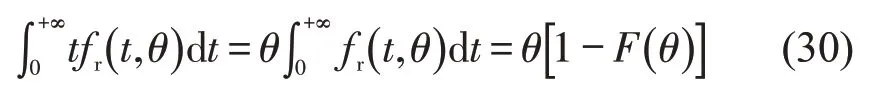
假设右转车辆在[0,Te]内服从均匀分布，即

将式(29)～式(31)代入式(28)可得

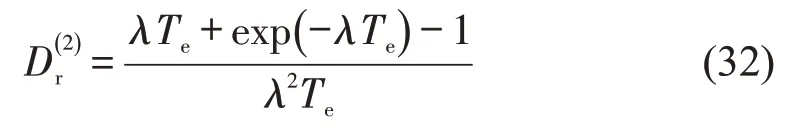
由于行人群的到达时距服从负指数分布，因此，相邻各行人群之间的时间间隔h大于某一值Hp的概率为

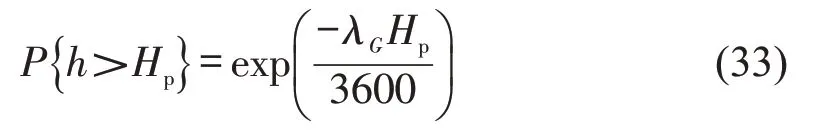
可得，单向行人流的可穿越间隙强度为

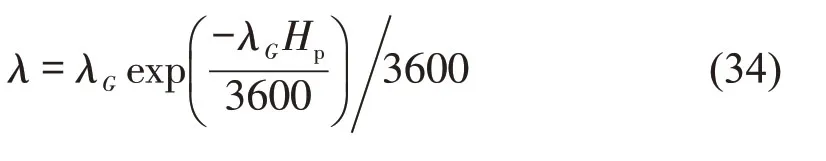
由于前文已假设不同方向通行的行人流为两个独立发生的事件，所以，双向行人流的可穿越间隙强度为

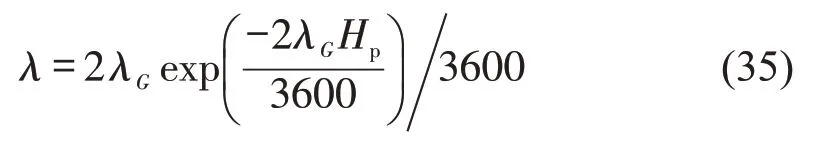
根据式(32)和式(34)，穿越行人流的每辆右转车平均延误为

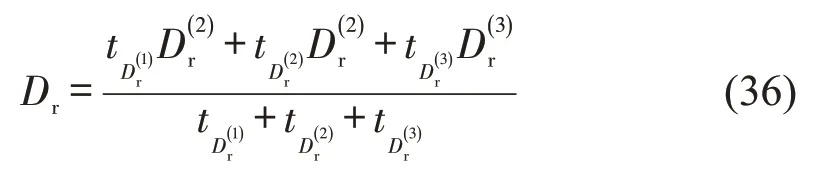
右转车穿越人流的延误过程如图6所示。

图6 行人随机到达时右转车辆延误过程Fig.6 Process of right-turn vehicle delay when pedestrians arrive randomly

5 案例分析

以行人过街绿灯时间和行人流量作为分析指标，交叉口信号配时如图7所示，通过计算对比设置行人二次过街前、后的R1的通行能力值，得出典型四相位交叉口右转车影响下的行人二次过街设置条件。

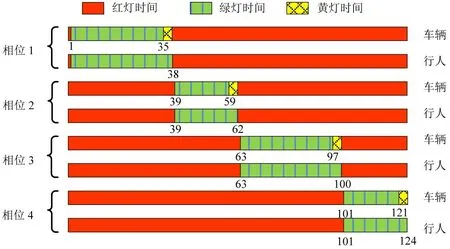
图7 交叉口信号配时示意图Fig.7 Illustration of signal timing of studied intersection

对昆明市人流量较大的10 个交叉口进行调查，单一流向的行人流量均在3000 人·h-1以下，取85%高峰行人流最大的小时流量为本算例的最大值。本文以双向6 车道的交叉口进行分析说明，每条车道取3.5 m，驻足岛宽度取2.5 m，人行横道宽5 m。

5.1 通行能力分析比较

(1)相同信号配时，不同行人流量下的行人二次过街设置前、后右转车通行能力比较结果如图8所示。

由图8(a)可得，在同一信号配时下，随着行人流量的增加，两种情况的通行能力均下降，且设置二次过街的通行能力更小；由图8(b)可以看出，随着行人过街流量的增加(增加至2000 人·h-1)，行人二次过街设置前、后的右转车通行能力差值逐渐减小而后逐渐增大，表明当行人流量处于范围的两端时，行人二次过街设置与否对右转车通行能力的影响较大。

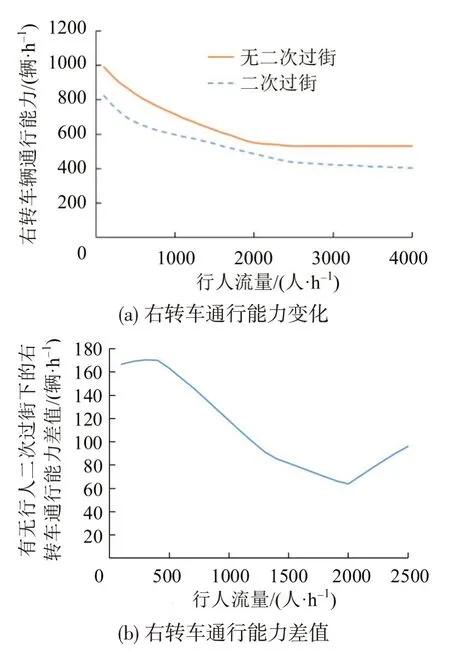
图8 相同信号配时参数和不同行人流量下右转车通行能力比较Fig.8 Comparison of right-turn vehicles capacity under same signal timing parameters and different pedestrian volume

(2)相同85%位的行人流量(1300 人·h-1)，仅增加直行相位时间的行人二次过街设置前、后右转车通行能力比较结果如图9所示。

由图9可得，在行人流量不变的前提下，随着直行相位时间的增加，未设置二次过街时的右转车通行能力均大于设置二次过街时的右转车通行能力；且两者差值出现下降的趋势，说明增大直行相位时间更利于二次过街设置时右转通行能力的增加。

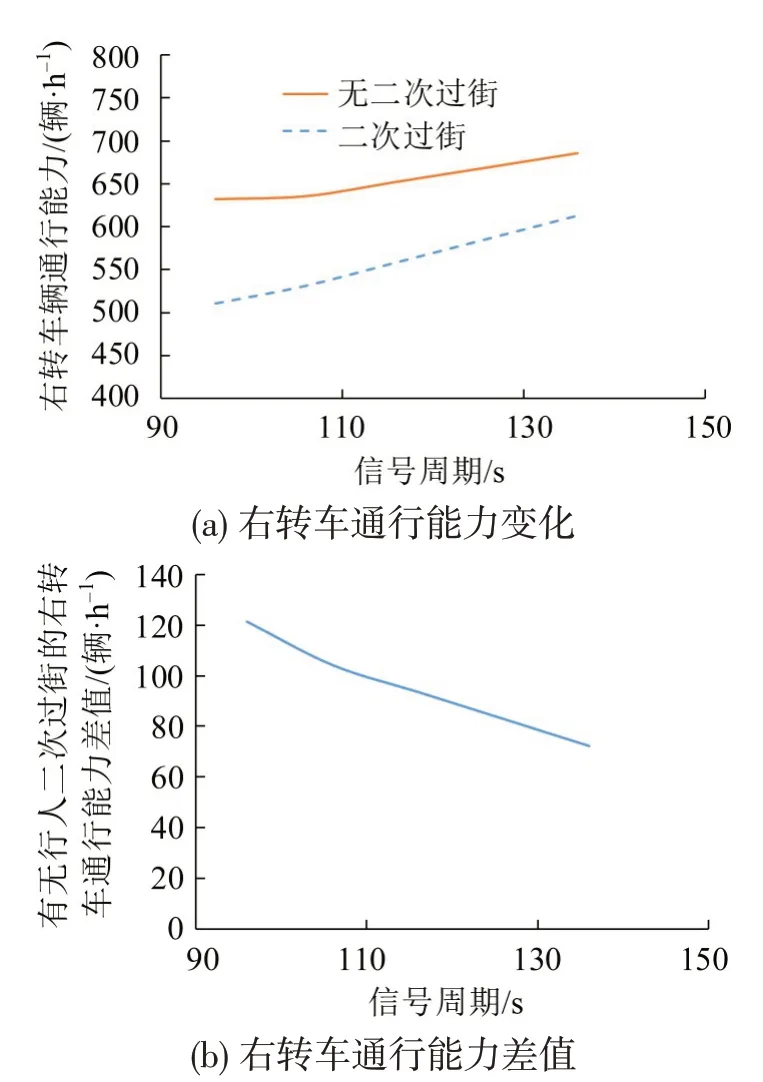
图9 在相同行人流量(1300 人·h-1)和不同信号周期(仅改变直行相位的绿灯时间)下右转车通行能力比较Fig.9 Comparison of right-turn vehicles capacity under same pedestrian volume(1300 pedestrians·h-1)and different signal cycles(changing green time of through phases only)

(3)相同85%的行人流量(1300 人·h-1)，仅增加左转相位时间的行人二次过街设置前、后右转车通行能力比较结果如图10所示。

由图10可以看出，当行人流量不变时，随着左转相位时间的增加，未设置二次过街时的右转车通行能力均大于设置二次过街时的右转车通行能力；且两者差值呈现出上升的趋势，说明增大左转相位时间更有利于未设置二次过街时右转车通行能力的增加。

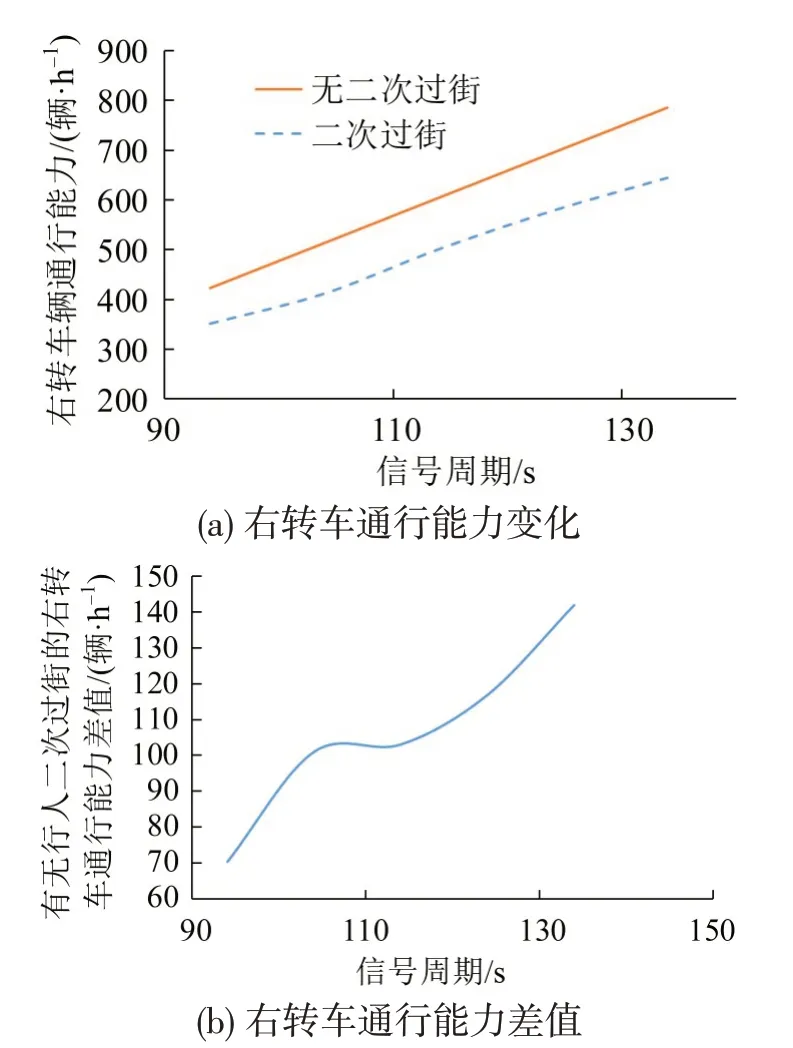
图10 在相同行人流量(1300 人·h-1)和不同信号周期(仅改变左转相位绿灯时间)下右转车通行能力比较Fig.10 Comparison of right-turn vehicles capacity under same pedestrian volume(1300 pedestrians·h-1)and different signal cycles(changing green time of left-turn phases only)

5.2 延误分析比较

(1)相同信号配时参数，不同行人流量下的行人二次过街设置前、后右转车延误比较结果如图11所示。

由图11可以看出，在同一信号配时下，随着行人流量的增加，行人二次过街设置时的右转车延误大于未设置行人二次过街时的右转车延误；但随着行人流量的进一步增加(增加至2000 人·h-1)，行人二次过街设置时右转车延误小于未设置行人二次过街时的右转车延误，表明，当行人流量处于较大值时，未设置行人二次过街对右转车延误的影响要大于行人二次过街设置时的影响。

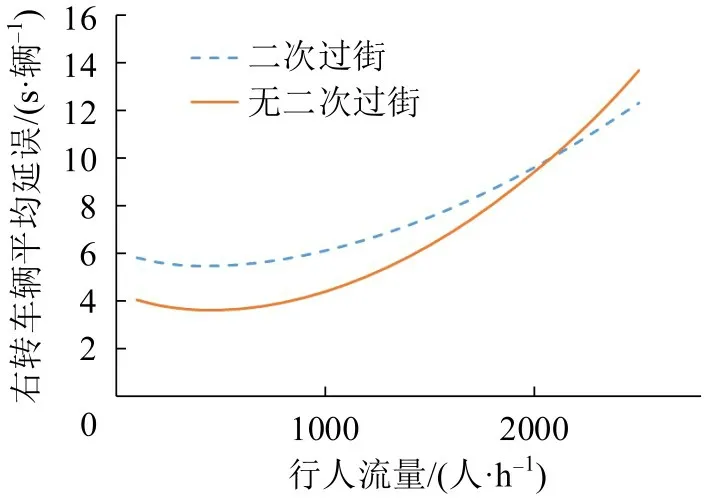
图11 在相同信号配时参数和不同行人流量下右转车延误Fig.11 Delay of right-turn vehicles under the same signal timing parameters and different pedestrian volume

(2)相同85%位的行人流量(1300 人·h-1)，仅增加左转相位时间的行人二次过街设置前、后右转车延误比较结果如图12所示。

由图12可以看出，当行人流量不变时，随着左转相位时间的增加，设置二次过街时的右转车平均延误要大于未设置二次过街时的右转车平均延误；但设置二次过街时呈现出下降趋势，未设置二次过街时呈现出上升趋势；表明，当行人二次过街设置时，左转相位时间的增加有利于减少右转车延误。

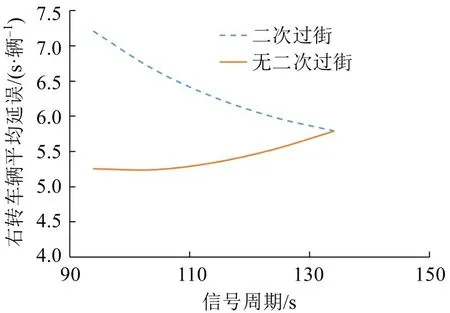
图12 在相同行人流量(1300 人·h-1)和不同信号周期(仅改变左转相位的绿灯时间)下右转车延误Fig.12 Delay of right-turn vehicles under same pedestrian volume(1300 pedestrians·h-1)and different signal cycles(changing green time of left-turn phases only)

(3)相同85%位的行人到达流量(1300 人·h-1)，仅增加直行相位时间的行人二次过街设置前、后右转车延误比较结果如图13所示。

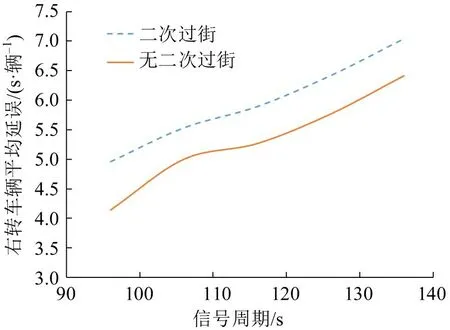
图13 在相同行人流量(1300 人·h-1)和不同信号周期(仅改变直行相位的绿灯时间)下右转车延误Fig.13 Delay of right-turn vehicles under same pedestrian volume(1300 pedestrians·h-1)and different signal cycles(change green time of through phases only)

由图13可以看出，在行人流量不变的前提下，随着直行相位时间的增加，未设置二次过街时的右转车延误均小于设置二次过街时的右转车延误；并且二次过街设置前、后的右转车延误均呈现出增大的趋势。

6 结论

本文利用可插车间隙理论和随机分布理论，建立了考虑行人冲突条件下右转车通行能力模型和延误模型。以典型的四相位信号交叉口为例，以行人流量、直行相位绿灯时间及左转相位绿灯时间为比较指标，比较分析了行人二次过街设置前、后右转车通行能力和延误。得到结论如下：

(1)总体而言，行人二次过街设置后，右转车的通行能力减小，延误增大，表明，行人二次过街的设置将增大右转车行驶压力。

(2)在行人流量相同的情况下，随着直行相位绿灯时间的增加，行人二次过街设置前、后右转车通行能力都将增大；此外，行人二次过街设置后，增加左转相位的绿灯时间更有利于提高右转车通行能力。

(3)在行人流量相同的情况下，随着直行相位绿灯时间的增加，行人二次过街设置前、后右转车延误都将增大；随着左转相位绿灯时间的增加，行人二次过街设置前的右转车延误将增大，行人二次过街设置后右转车延误将减小。本文分析方法可推广到其他相位放行方式(例如，单口放行)分析右转车与行人过街的冲突；适用于分析非机动车较少或无非机动车的信号控制交叉口，可以为是否采用行人二次过街，是否对右转车采用信号控制及是否设置行人专用相位等信号优化方法提供理论支撑。