基于航空器自主运行的空中交通复杂性建模

王红勇，郭宇鹏

(中国民航大学，空中交通管理学院，天津 300300)

0 引言

随着航空业在后疫情时代逐渐复苏，未来全球空中交通量有望持续增长，空中交通管理(Air Traffic Management,ATM)系统有限的空域服务能力将成为限制航空运输发展的关键瓶颈。基于自由航路空域(Free Route Airspace,FRA)的航空器自主运行模式为克服上述问题提供新的思路。自由航路空域是欧洲单一天空项目(Single European Sky ATM Research,SESAR)的重要组成部分，航空器可在选定空域进出点后直飞穿越该空域[1]。在自由航路空域中，空中交通管理将发展为地基ATM系统与机载系统并用，由机载系统根据空域运行态势辅助飞行员完成战术航迹规划，实现航空器自主运行[2]。在此模式下，空域运行态势的评价主体为机载系统，评价对象将由航线(航段)拓展至空域中任意点。

空域运行态势可通过空中交通复杂性反映，是航空器成功实施自主运行的基础。国内外研究者在基于客观运行数据表征空中交通复杂性方面做了大量尝试。Delahaye等[3]提出了基于航迹数据量化计算复杂度的方法，Hasan 等[4]基于Lyapunov 指数测量了空中交通几何结构复杂性，丛玮等[5]使用灰色关联聚类方法研究复杂性指标的选取和精炼过程，王红勇等[6]率先建立了空中交通态势复杂性的二维、三维网络模型，吴明功等[7]通过典型复杂网络拓扑指标实现了空中交通复杂性的识别与表征。为应对航空器自主运行模式对空中交通复杂性提出的新需求，Brázdilová等[2]设想了基于分布式空中交通管理系统实现航空器自主保持间隔运行的场景，并简要构建基于该模式的空中交通复杂性计算模型，陈雨童等[8]通过可视图法和Dijkstra算法研究受限空域自主运行模式，以总飞行距离最短为目标进行航空器路径与速度联动规划。

综上，现有空中交通复杂性研究侧重于地基模式的集中式空中交通管理，部分针对航空器自主运行的研究，侧重于空域宏观运行态势评估，难以满足自主运行模式下实时测度空域中任意位置复杂度分布的需要，也无法为机载分布式ATM 系统进行航迹优化提供依据。同时受机载数据链和计算机性能限制，空域复杂性的测度方法不能过于繁琐。为此，本文将探讨一种适用于航空器自主运行的空中交通复杂性快速计算方法，并通过实际管制扇区数据进行仿真验证。

1 建模

1.1 空域栅格化建模

航空器自主运行模式下，可将空域离散化为若干大小一致、相互连接的基本空域体单元，每个单元在空中交通数据管理中相对独立，称其为空域格网单元[9]。格网单元是特定形状的空间体，边界点坐标由栅格形状、尺寸、经(x轴)纬(y轴)度及高度(z轴)决定。考虑空域复杂度的实时变化特性，需在计算效率和精度之间做出权衡，权衡的实际指标包括扇区大小、栅格形状、栅格尺寸等。为与空中交通管理实际运行标准相符，本文选择水平间隔10 km，垂直间隔300 m 的长方体栅格划分空域。基于此标准对某空域及空域中某航空器航迹进行栅格化处理，如图1所示。

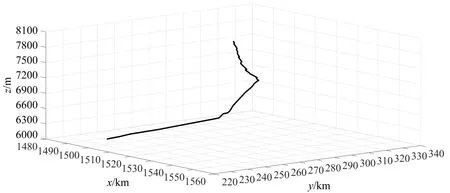
图1 空域栅格化示意图Fig.1 Schematic diagram of spatial rasterization

基于栅格的空域离散化建模主要实现以下功 能：(1)对航空器的航迹进行离散化处理，便于标示航空器四维时空位置；(2)实时测度每一栅格的空域复杂度值，并以此反映空域运行态势；(3)比选航空器初始航迹邻近栅格的复杂度值，以便进行航迹优化。

1.2 空域复杂性建模

为更客观地反映空域内各航空器相对空域各点的汇聚程度及汇聚趋势，本文将空域中某一位置点的实时复杂性定义为当前时刻空域中航空器对该点施加的影响大小。假定某栅格中心点C，构建其复杂性影响空域如图2所示。该空域为水平面长半轴、短半轴长度均为a，垂直高度为2h的椭球体。A为某航空器i所处位置，P为CA连线所在向量与椭球边界的交点，箭头方向为航空器运动方向，γ为与航空器运动方向的夹角。

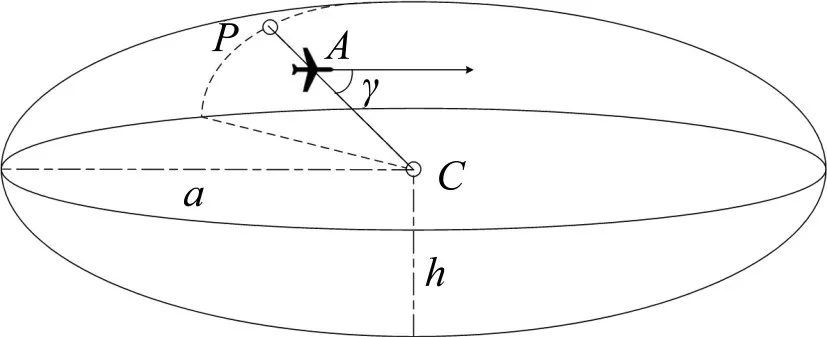
图2 空中交通复杂性影响空域示意图Fig.2 Schematic diagram of airspace affected by air traffic complexity

设t时刻，空域内共有n架航空器，则航空器对点C施加的叠加复杂度为

式中：M(C,t)为t时刻C点处的整体复杂度值；mi(t)为t时刻第i架航空器对C点的复杂性影响，即单机复杂度值，计算公式为

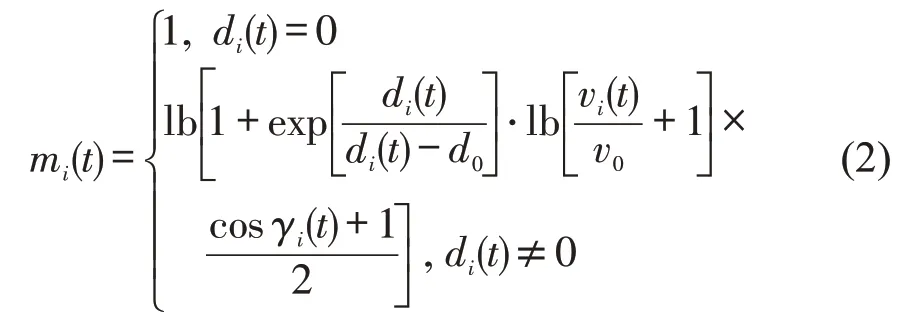
衡量了航空器位置、速度、航向对于复杂度值的影响；vi(t)为t时刻航空器i的航速；v0为预设的参考航速值；γi(t)为t时刻航空器i的航向与的夹角(以弧度制表示)；di(t)为t时刻航空器i所处位置相对点C的距离，为避免航空器水平间隔和垂直间隔的计量标准不同造成点-机临近程度判定结果存在差异，本文引入椭球距离概念，即

式中：Δxi(t)、Δyi(t)、Δzi(t)分别为t时刻航空器i所处位置相对C点的纵向距离、侧向距离与垂直距离；a、h分别为椭球体的水平半轴与垂直半轴长度，亦为预定义的复杂性水平影响范围与垂直影响范围；d0为预设的复杂性影响范围，计算公式为

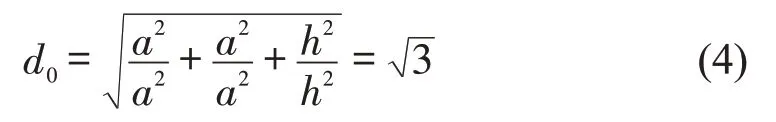
由式(2)可知，若t时刻航空器i恰好处于C位置，则设定其对于C点的复杂度为1。若航空器所处位置不属于点C对应的复杂性影响空域，即当Δxi(t)＞a或Δyi(t)＞a或Δzi(t)＞h，亦或di(t)＞d0时，设定mi(t)=0。

1.3 模型分析

由认知可得，航空器位置越接近点C、航速越高、航向与夹角越小，则航空器对点C的复杂性影响理应越大。基于当前设备性能限制，本文对航空器复杂性影响水平范围a的设定标准，参考第二代航空器机载防相撞系统(Traffic Alert and Collision Avoidance System Ⅱ，TCASⅡ)主动询问方式下的监视范围40 nm[10]，约合70 km。对于垂直距离h的设定标准，参考我国当前高度层划分标准——12500 m高度以下同向高度层划分间隔标准为600 m。即a=70 km，h=600 m，若di(t)＞，则认为该航空器对点C不存在复杂性影响。基于BADA 数据库中波音737 型客机经济巡航速度828 km·h-1与最大运行速度876 km·h-1[8]，本文假定航空器航速范围800～900 km·h-1，并设定最高参考航速为900 km·h-1。夹角γ取值介于(0,π)；当夹角处于(0,π 2)时，航空器航向分量与方向相同，航空器向C点汇聚；当夹角处于时，航空器航向分量与方向相反，航空器背离C点飞行。

根据式(2)计算单架航空器对于周边空域的复杂性影响，以及水平对向偏置飞行的4架航空器在连续飞行时段内对水平空域的复杂性影响，分别如图3和图4所示。

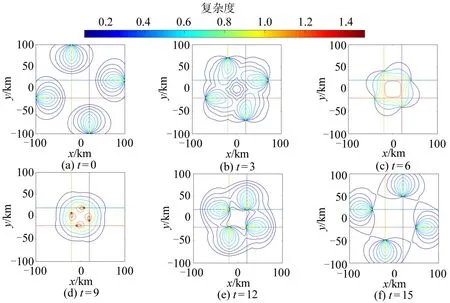
图4 4架航空器水平对向偏置飞行对空域周边空域复杂度影响Fig.4 Influence of four aircraft flying in horizontal convergence on complexity of surrounding airspace

图3(a)为复杂度水平截面图，同心叶型线为航空器对水平方向各点施加的复杂度等值线；图3(b)为沿航空器航向方向的复杂度垂直截面图，标示航空器对垂直方向各点施加的复杂度。如图可见，航空器对航向前方空域的复杂性影响高于其他方向，对航向后方空域的复杂性影响不断削减至0。

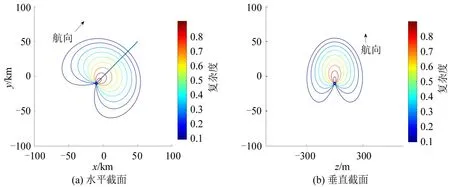
图3 单架航空器对周边空域复杂性影响Fig.3 Influence of a single aircraft to complexity of surrounding airspace

图4(a)～(f)显示水平对向偏置飞行的4 架航空器对水平空域的复杂性影响随时间变化趋势。图4(a)中各航空器间距较远，复杂性影响未叠加；随时间推移，各航空器不断接近，复杂性影响逐渐叠加，因此导致图4(c)和图4(d)中某些位置复杂度过高；至航空器交错后，叠加影响逐渐消除。且由图4可见，图4(b)和图4(f)，图4(c)和图4(e)中航空器间隔相同而运行方向不同，其对于空域复杂性影响也有显著区别。

2 仿真验证

2.1 仿真空域选择

本文选取上海区域管制中心1 号管制扇区(ZSSSAR01)中使用率较高的8900，9200，9500，9800 m高度层作为仿真空域，模拟固定航路和自由航路运行模式。向东运行的航空器选择8900 m和9500 m 高度层，向西运行的航空器选择9200 m 和9800 m 高度层。随机生成100 架航空器的航迹并为每一航空器设定进入扇区时间和高度层。固定航路运行模式下航空器由设定的航路点进出扇区，并假定同高度同航迹航空器进入扇区的时间间隔大于5 min。自由航路运行模式下航空器随机选择与固定航路模式相对应的同方向扇区边界点进出。由于航空器在航路中一般保持固定高度匀速飞行，故仿真中假定每一航空器的速度保持恒定，且不考虑航空器穿越高度层。两种运行模式对应航迹如图5所示。

图5 模拟空域运行航迹图Fig.5 Track map operating in simulated airspace

图5为航迹俯视图，包含4 个高度层所有航空器的航迹。图5(a)和图5(b)分别表示固定航路和自由航路运行模式。图示可见，自由航路模式的航迹分布较固定航路模式更为分散，同向运行的航空器航迹存在横向偏差。

假定各航空器在扇区中保持匀速运行，计算各航空器实际运行时间ti，总运行时间Ti=t(0)i +ti，并将总运行时间最大值MaxTi设定为总仿真时间。对总仿真时间以10 s为单位离散成时间片，计算每一时间片对应空域各栅格的复杂度值；对其取平均数作为该时刻扇区平均复杂度值。其中某时间片内9200 m、9500 m 高度层的复杂度等值线分布如图6所示，部分时间片对应的扇区最大复杂度值和平均复杂度值对比如表1所示。

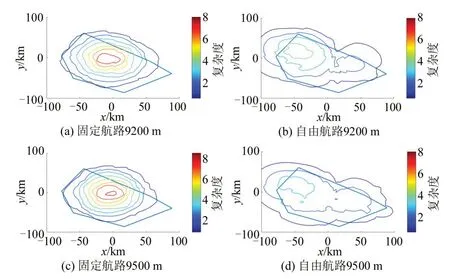
图6 某时刻空域运行状态Fig.6 Airspace operation status at a certain time

图6(a)和图6(c)为固定航路运行模式下9200 m、9500 m高度层的复杂度分布，由于同向运行的航空器选择相同的航路，航空器间的水平间隔较小，扇区内繁忙区域的复杂性影响存在明显叠加；对比图6(b)和图6(d)自由航路运行模式下9200 m、9500 m 高度层的复杂度分布，其航迹横向分散，航空器聚集现象不明显，不存在复杂性影响过度叠加的区域。表1所示扇区复杂度指标中，两种运行模式对应的扇区最大复杂度差异远大于平均复杂度差异；固定航路运行模式对应的扇区最大复杂度与平均复杂度的差异远大于自由航路运行模式。表明自由航路运行模式下，航空器在扇区内横向分散，各高度层各栅格内航空器分布较为均衡，不存在过度闲置的空域，空域资源利用效率较高。

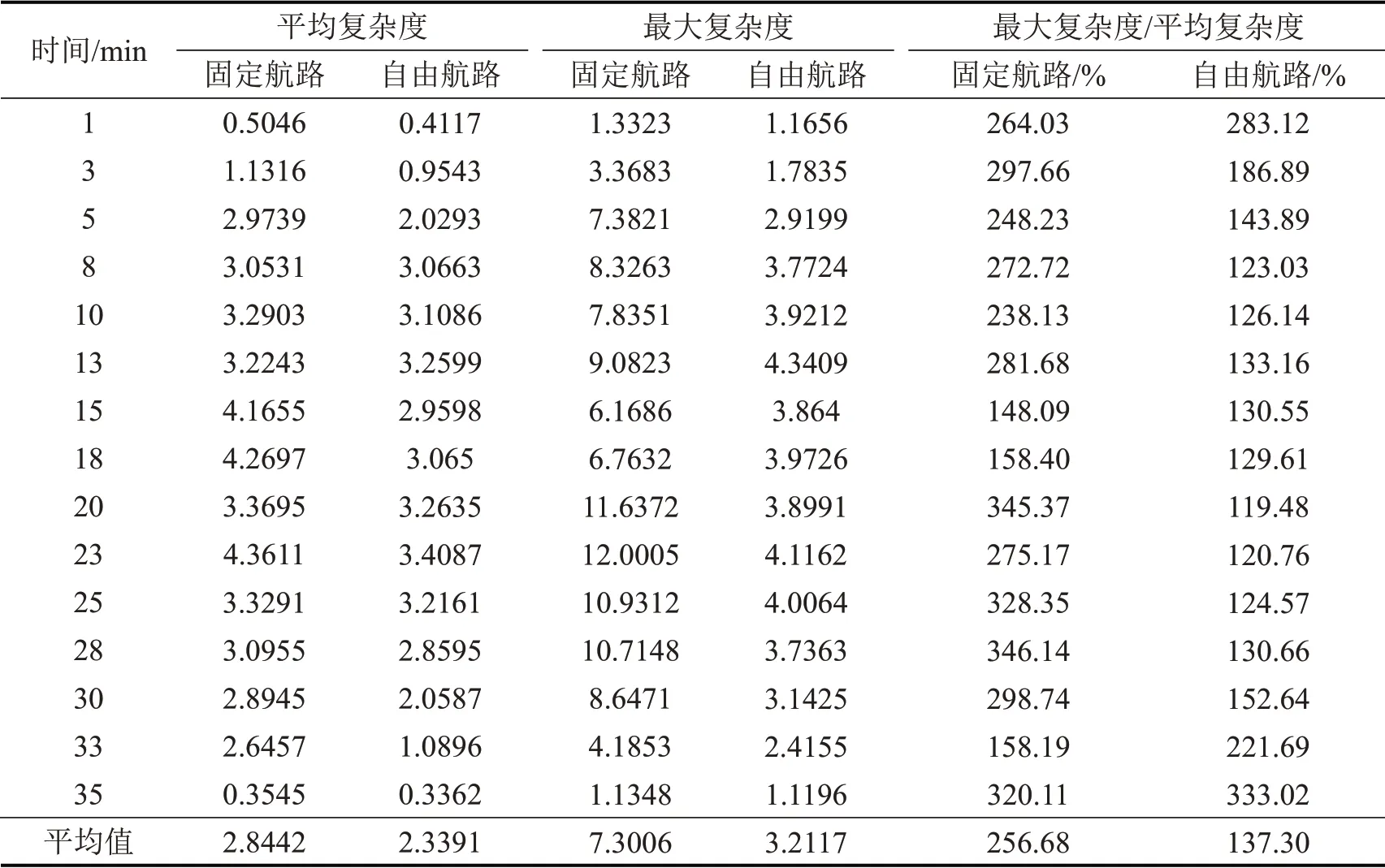
表1 固定航路和自由航路运行模式扇区复杂度对比Table 1 Comparison of operation mode complexity between fixed route and free route airspace

2.2 空域复杂度与冲突

航空器潜在冲突指两架航空器间隔小于规定的间隔标准。我国对于航空器是否发生飞行冲突的间隔标准设定为水平方向10 km、垂直方向300 m。在自由航路运行模式下，航空器可根据(飞行员、航空公司等的)偏好自主规划航迹，由此也会带来航空器时空位置不确定及潜在冲突数量上升等问题。这里将基于新提出的复杂度模型，探讨自由航路运行模式下空域复杂度值与航空器冲突的相关关系。选择冲突率(冲突次数/航班总数)和冲突比例(冲突航班数/航班总数)作为衡量冲突发生强度的指标。各时间片内航空器冲突指标和扇区平均复杂度值的关系如图7所示。

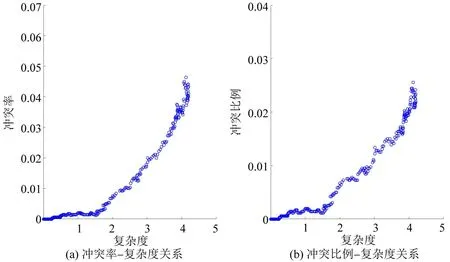
图7 冲突指标-空中交通复杂度值关系Fig.7 Relationship between flight conflict rate and air traffic complexity value

图7(a)反映航空器冲突率-复杂度关系，图7(b)反映航空器冲突比例-复杂度关系。可见航空器冲突率、冲突比例均与空域复杂度值有相似的变化趋势。为验证该数量关系，基于上述空域和自由航路运行模式进行20 次重复实验，并计算各组实验对应冲突指标与扇区平均复杂度值的相关系数，再由此计算相关系数均值和变异系数，如表2所示。

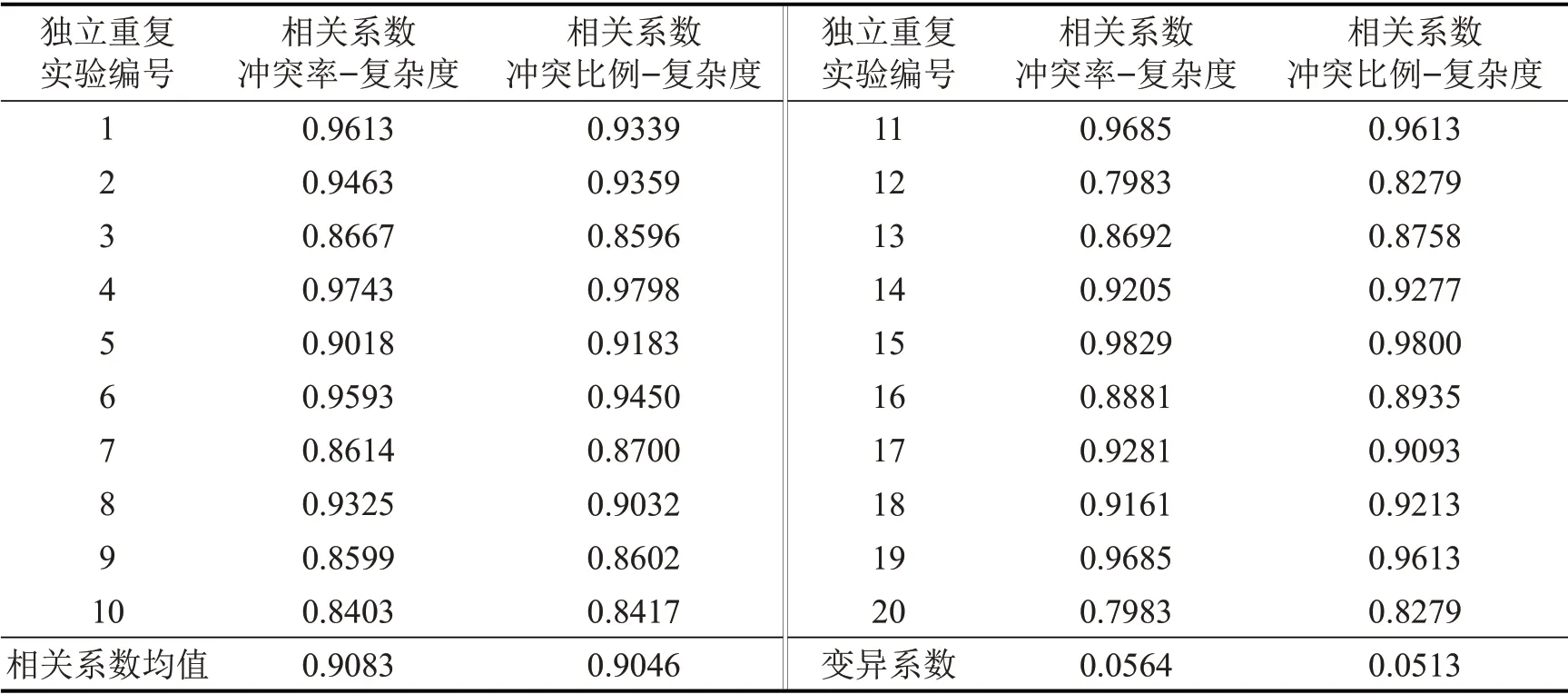
表2 各组实验所得冲突指标-复杂度值相关系数Table 2 Correlation coefficient of conflict index and complexity value obtained from each group of experiments

据表2所示，20 次独立重复实验结果表明，冲突次数与复杂度值、冲突航班数与复杂度值之间均有较强相关性(相关系数平均值大于0.90)；重复实验所得数据的变异系数较低(小于5.7%)，表明该数据分布较为集中，冲突指标与复杂度值的相关关系具有非偶然性。上述结论表明，冲突指标与复杂度值具有稳定的强相关关系，可用空域复杂度值大小表征并预测空域未来冲突可能性。

2.3 潜在应用

本文提出的复杂度模型可应用于自由航路运行模式的航空器战术航迹规划中。在该运行模式下，航空器基于自身偏好设定初始航迹，在运行中实时计算邻近空域栅格的复杂度值，并据此判定冲突发生的可能性。若复杂度值较高(超过该空域的复杂度阈值)，则发生冲突的可能性较大，可通过机载分布式ATM 系统辅助飞行员进行航迹调整，以此实现航空器自主保持间隔运行。为保障运行安全，本文选取各时间片内扇区最大复杂度上0.8 分位数作为该空域的复杂度阈值。基于上述空域和自由航路运行模式进行20次重复实验以确定该扇区复杂度阈值，计算结果如表3所示。

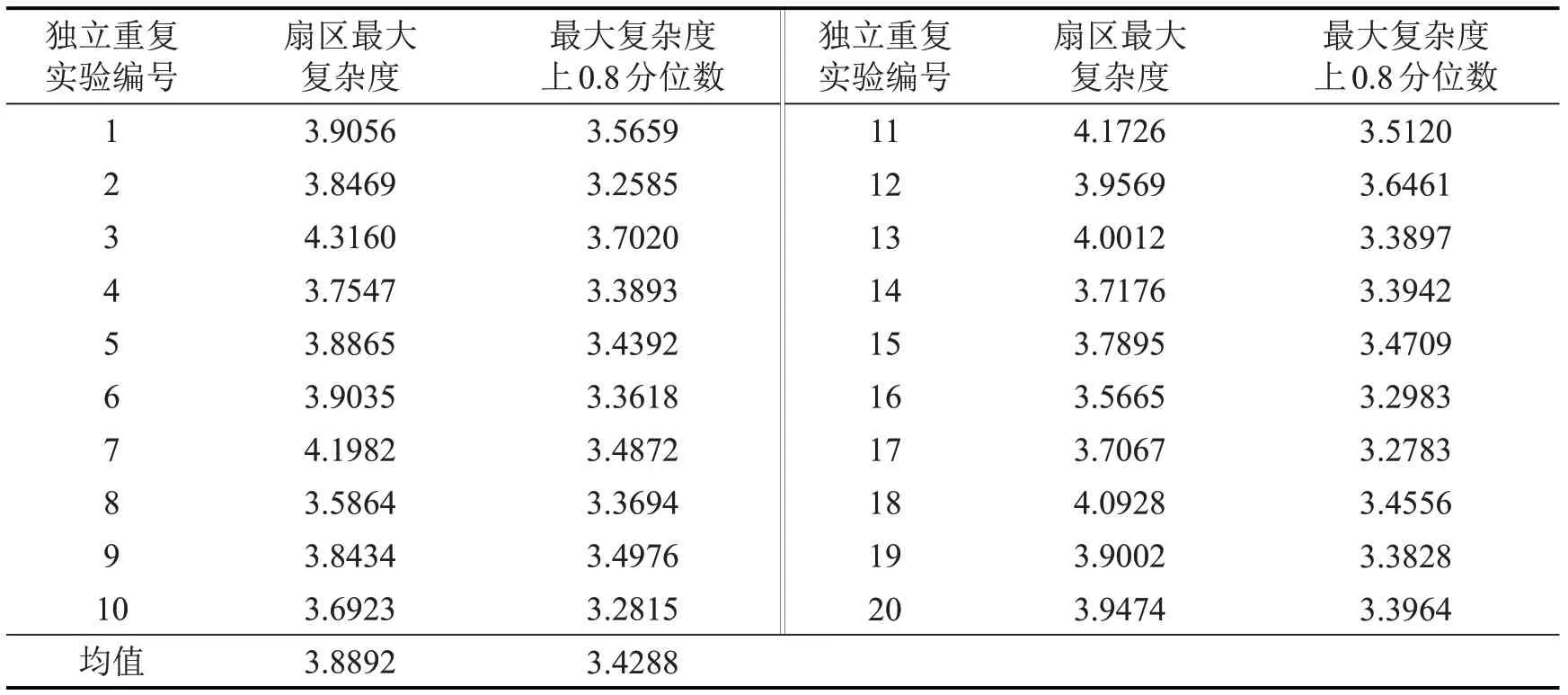
表3 各组实验所得扇区最大复杂度及上0.8分位数Table 3 Upper 0.8 quantile and maximum sector complexity obtained by each group of experiments

若某一时刻部分栅格的复杂度值超过阈值(3.4288)，表明此时刻该栅格内冲突可能性高，应限制其他航空器进入该栅格。在航空器自主运行模式下，若航空器探测到初始航迹某区域的复杂度值超过复杂度阈值，即表明有较高冲突风险时，机载分布式ATM系统将辅助飞行员在规则允许范围内调整航迹，选择复杂度值较低的区域以保证安全。

如图8所示，航空器初始航迹中部分栅格的复杂度值高于阈值(3.4288)，机载系统将辅助飞行员进行航迹调整，选择空域内复杂度值较低的栅格作为改航点以规避高复杂度区域。航迹调整效果如表4所示。航迹调整后，航迹最大复杂度与航迹平均复杂度均得到显著降低。结果表明，基于空域复杂度的战术航迹调整策略可有效规避高复杂度空域。

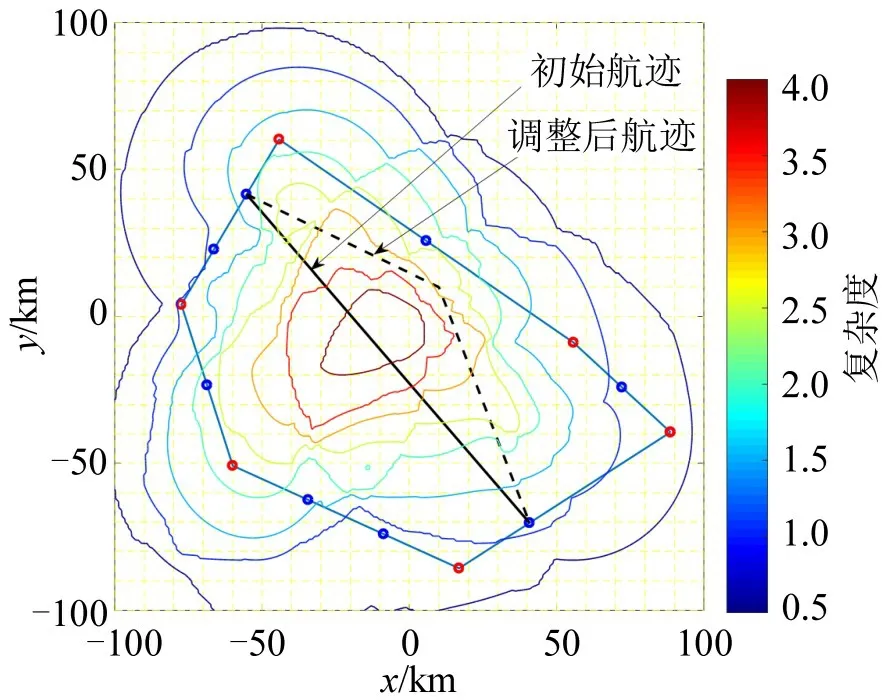
图8 基于空域复杂度进行航迹实时优化示意图Fig.8 Schematic diagram of real-time path optimization based on spatial complexity

表4 基于复杂度的航迹调整效果Table 4 Results of track adjustment based on complexity

3 结论

本文结论如下：

(1)提出适用于航空器自主运行模式的复杂度计算模型，可反映航空器位置、速度、航向因素对于空域某栅格的复杂性影响。

(2)基于ZSSSAR01 扇区验证了自由航路运行模式的复杂度时空分布较固定航路运行模式更均衡。

(3)复杂度值对于航空器冲突的相关性可达0.90以上，表明该方法在航空器自主保持间隔运行的冲突探测中具有较好的适用性。

本文提出的复杂度计算方法暂时只应用于航路，未来可拓展至终端区等航空器易出现大范围高度变化的区域；本文仿真实验中基于TCASⅡ系统确定复杂性水平影响范围，未来实现ADS-B 与TCAS 混合监视后，监视范围大大增加，也可拓展本文中复杂性影响范围以实现更长时间的空域运行态势预测；本文仅提出了空域复杂度应用于分布式ATM 系统实现航迹实时优化的理念设想，未来可对于改航点和回航点选择、三维高度自主调配等问题开展进一步研究。