基于链路预测的中小机场连接机制研究

张培文，杜福民，汪瑜*

(1.中国民用航空飞行学院，经济与管理学院，四川广汉 618307；2.西南财经大学，统计学院，成都 611130)

0 引言

探索中小机场航线选择的影响因素，揭示中小机场航线选择规律，是研究中小机场航线连接机制的重要内容。截止到2020年底，我国民用运输机场数量达到241 个，但年旅客吞吐量不足200 万人次的中小机场数量占全部机场总数的近80%，其吞吐量仅为机场总量的10%。年旅客吞吐量超过1000 万人次的大型繁忙机场数量仅占机场总数的11%，其吞吐量却占机场总量的70%。在中小机场和大型机场之间发展极不平衡的形势下，探索中小机场发展普遍困境，提高其航线选择和网络布局的合理性，对于改善我国航线网络的通达性，充分发挥运输网络的运行效率和效益，以及实现中国民航局“十四五”时期“一二三三四”战略有着重要的现实意义。

国内外学者对网络连接机制从不同角度进行了研究，Barabási 等[1]最早提出了一种基于优先连接机制的无标度网络演化模型(BA模型)，王杰等[2]利用改进的BA模型分析了不同规模海运网络的演化机制情况。但不同网络机制之间的优劣性难以判断，因而链路预测的出现为网络连接机制提供了统一且公平的比较方法。在航空网络中，刘宏鲲等[3]比较了多种节点属性接近性因素，指出第三产业产值对航线网络演化机制影响较大；冯霞等[4]同时考虑航线网络的拓扑结构和节点属性两类特征，提出基于链路预测的未来新增航线发现模型；Takahashi等[5]从航线网络不同结构接近性的角度，评估了各种链接预测方法之间的相对预测精度；Najari等[6]探讨了多层航空网络层间结构的接近性并对层间节点进行连接可能性预测。以上研究对航线网络连接机制的探讨多针对整体网络，而中小机场在整体网络中的地位处于弱势特征，未能关注到中小机场在航线网络中的连接机制问题，对预测结果也缺乏实际验证与应用。

本文考虑影响中小机场航线连接的外生属性，同时选取网络的结构性特征作为内生因素，比较内外影响因素的链路预测精确度，确定不同因素对航线连接的影响程度，并选取精确度高的内外因素进行多因素耦合预测，验证耦合算法的有效性并进行实际验证，以期更为全面且有针对性地挖掘中小机场的重要连接机制。

1 问题描述与评价指标

1.1 问题描述

本文航线数据来源于2019年民航局公布的夏秋航季全国航班计划总表，以连接中小机场的航线为边构建出无向的中小机场航线网络。对吞吐量高于200 万人次的多机场城市的航班数据进行合并，数据不包含港澳台地区。数据经处理后判别出中小机场159 个，与中小机场相连的航线1588 条，网络共包含224个机场。

令V为点集，E为边集，则生成的中小机场航线网络可表示为G(V,E)，同时所有节点对的全集为对于一种链路预测算法，为所有未产生航线连接的节点对(x,y)赋予分数值vxy，这种分数值可视为一种接近性，分数值越高的节点对连接可能性越大。为检验算法的准确性，将边集E随机分为训练集ET以及测试集EP，数据集满足于E=ET∪EP，ET∩EP=∅[7]，前者主要作为已知信息计算分数值，后者用以连边测试。

1.2 评价指标

中小机场航线网络是一个整体，因而从预测的完整性角度考虑，本文选取从全局角度衡量预测算法精确度的AUC(Area Under Curve)指标评价算法的准确性。其基本原理为：一种接近性算法经过训练后可以得到网络中所有节点对间的接近性矩阵，然后利用AUC 指标以网络中不存在的边为基准，每次随机选择不存在边的接近性值与EP中的边进行比较。若EP中选择的边分值更高则记1 分，分值相等则记0.5 分，小于则不记分。显然抽取次数越多，得到的AUC越精确。在进行m次比较以后，若有m1次记1分，m2次记0.5分，则AUC的具体测度定义为

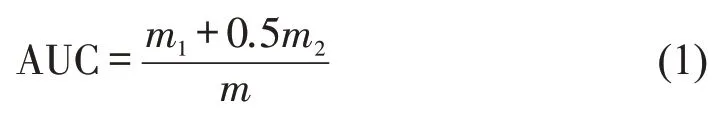
其中，若所有分数均随机产生，则AUC≈0.5，当AUC=1 时，表示算法准确预测出所有结果。因而AUC 大于0.5 时算法便具备一定可行性，接近1的程度则反映出当前预测算法的准确性。此外，ET的选取比例也会影响AUC计算结果，一般ET划分比例越高，AUC值越大。因而本文判别当ET∶EP=9∶1时，AUC对不同算法的预测精确度评价情况。

2 中小机场航线网络的链路预测

2.1 网络外生属性的接近性

中小机场发展好坏受自身、社会、经济等因素的影响，以上因素可以构成中小机场航线网络的外生属性。在获得节点相关数据的情况下，从节点属性角度进行链路预测同样值得关注。本文选取机场间航距反映其连接属性，以机场的起降架次反映其自身属性，以机场所在城市的人口数量、第三产业产值反映其社会、经济属性，4种外生属性接近性指标具体如下。

(1)航距(Flight distance,Fld)的接近性

航距对航线网络的连接有着明显影响，航线的数量会随着航距的增加逐渐上升，当航距达到某一值后，航线的数量又逐渐减少[3]。但航线两端机场的连接可能性并不能仅以现实航线数量分布进行考虑，为了分析航线的航距与航线连接的可能性之间的关系，本文对中小机场航线网络中所有节点间的连接按距离进行统计，以真实存在的不同航距的航线数量与该航距下总的航线数量的比值作为连接率，并对连接率分布趋势进行拟合，拟合曲线如图1所示，拟合优度为0.9757，表明该曲线能够较好地反映航距对机场间连接可能性的影响。由于航距低于200 km 的航线数量极少，故未对其进行拟合。从航距角度用拟合函数将其接近性定义为

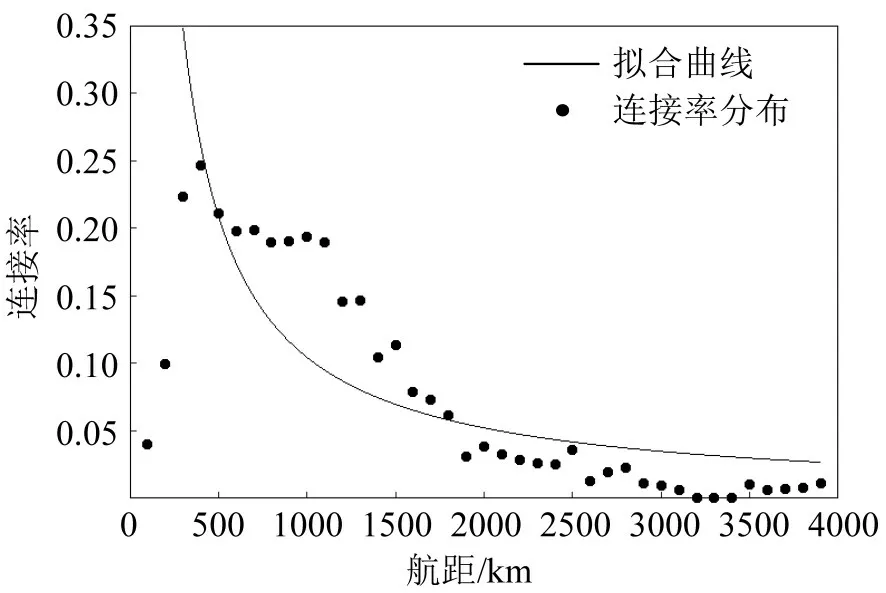
图1 不同航距航线连接率拟合曲线Fig.1 Fitting curve of connection rate of routes with different distances

式中：F(x,y)为机场x与机场y的航距。

(2)起降架次(Sortie,Sor)的接近性

机场的起降架次能反映其繁忙程度，是机场业务量的重要统计特征之一。一般而言，起降架次高的机场能获得更高的客运或货邮吞吐量，越能吸引其他机场的连接，新增的航线也就越多，使得机场的整体连通性获得提升，而连通性的提升又反过来使得机场更为繁忙，最终产生“强者越强”的现象。这种“强者越强”的连接现象，可以通过一个优先连接模型描述起降架次的接近性[8]，即

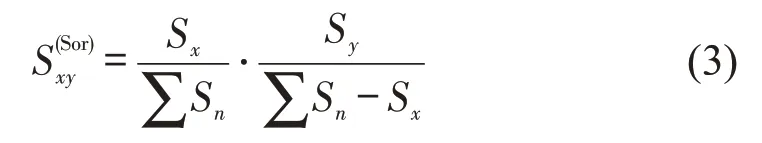
式中：n为机场数量；Sx为机场x的起降架次数量；Sy为机场y的起降架次数量；Sn为n个机场的起降架次数量。式(3)表示两机场在起降架次因素影响下相互选择的概率，在本文链路预测方法中指起降架次的接近性。

(3)人口数量(Population,Popu)的接近性

在使用航空出行概率相同的情况下，每个目的城市都有相同几率被选择，机场所在城市的人口数量越多，则两城市间的人员流动密度越高。人口数量同样具有“强者越强”的特征，因而人口数量的接近性表示为

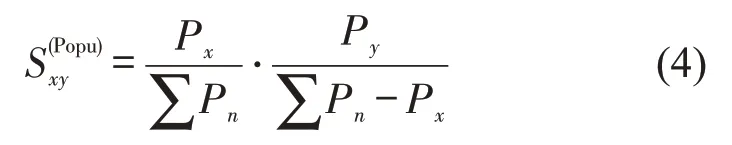
式中：Px为机场x所在城市的人口数量；Py为机场y所在城市的人口数量；Pn为n个机场所在城市的人口数量。本文所使用的城市人口数据为年平均人口，人口及下文的第三产业产值数据均来源于《中国城市统计年鉴2020》。

(4)第三产业产值(Tertiary Industry,TI)的接近性

由于航空运输与服务业息息相关，同时已有研究从城市GDP以及第三产业的接近性角度研究了整体航空网络的预测性，发现第三产业的接近性更好[3]，因此从中小机场航线网络中机场所在城市的第三产业角度建立网络连接的接近性模型，即

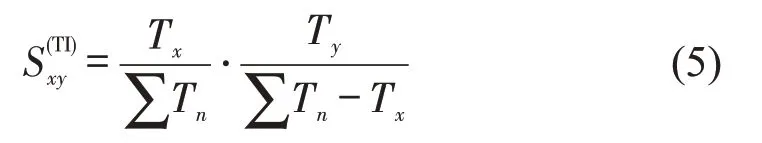
式中：Tx为机场x所在城市的第三产业产值；Ty为机场y所在城市的第三产业产值；Tn为n个机场所在城市的第三产业产值。

2.2 网络内生因素的接近性

网络中两个节点是否连接除受自身属性影响外，网络结构特征也是重要影响因素，因而有必要从网络结构信息角度进行发掘。从网络结构信息角度定义的接近性，一般称为结构接近性，本文指网络内生因素的接近性。一种结构接近性能否很好地抓住网络的结构特征，决定了该结构接近性最终链路预测精度的好坏。现有研究发现，一个网络的集聚系数小于阈值0.1 时，基于全局信息的接近性算法预测效果较好[9]。对中小机场航线网络的结构特征参数进行统计，结果如表1所示，可以发现，其集聚系数未达到0.1，故从全局信息接近性研究中小机场航线网络的链路连接机制是本文的主要角度。本文按上述算法的类别，选用以下4种典型算法探究中小机场连接机制。

表1 中小机场航线网络结构特征参数统计Table 1 Statistics of characteristic parameters of small and medium-sized airports network

(1)优先连接(Preferential Attachment,PA)

PA指标主要是从两个节点度值的乘积角度定义两节点间的接近性，也就是各节点度值越高则相互连接的可能性越大。应用优先连接方法可以产生无标度的网络结构，而中小机场航线网络度值分布符合幂律特征，PA 指标可表示机场节点度值与网络连接性的关系，公式为

式中：Kx为节点x的度值；Ky为节点y的度值。

(2)局部路径(Local Path,LP)

局部路径是考虑网络三阶路径的基础上提出的接近性指标，表示为

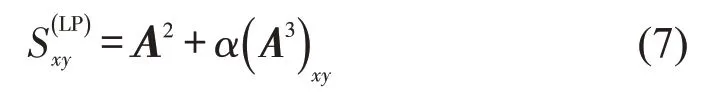
式中：α为可变参数；A为网络的邻接矩阵；A3xy为两节点间路径长度为3 的数量。此处局部路径是3 阶路径，在其基础上也可以扩展到更高阶路径的情形，但随着阶数增加，指标的计算复杂性会越高。

(3)平均通勤时间(Average Commute Time,ACT)

对于一个随机游走粒子，由节点x至节点y的平均步数为m(x,y)，则两节点间的平均通勤时间可表示为n(x,y)=m(x,y)+m(y,x)。n(x,y)可通过求解网络的拉普拉斯矩阵L(L=D-A)的伪逆L+得到，其中，D为网络的度矩阵。于是平均通勤时间的接近性可以理解为两节点的通勤时间越小，节点间越接近，表示为

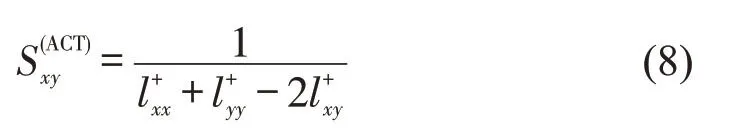
式中：l+xx为矩阵L+中第x行y列所在位置的元素。

(4)重启随机游走(Random Walk with Restart,RWR)

若一个随机游走粒子每走一步都有可能以概率c返回其初始位置。粒子从节点x处走到节点y处的概率可用网络的马尔科夫概率转移矩阵表示，其中，kx为粒子在节点x处的状态向量，若两节点相连则axy=1，反之为0[7]。某粒子在初始节点x处，在下一时刻到达网络中任一节点的概率向量为

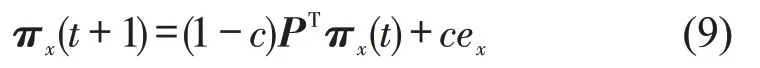
式中：t为时间；PT为概率转移矩阵的转置；ex为初始状态。求得式(9)的稳态解为

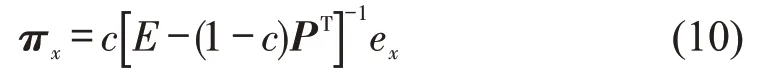
于是可将重启随机游走接近性的定义为

式中：πxy为由节点x出发最终到达节点y的概率。

2.3 接近性算法精确度分析

中小机场航线网络中224 个节点处于全联通状态时，边数为24976条，当前未知连边数为23388条。在保证训练集连通性的情况下，训练集划分比例为90%，测试集划分比例为10%，测试边数量为159条。在进行AUC计算时，一般采用抽样的方式节省计算时间，本文抽样次数为300000次，计算出300000次抽样时实验的AUC值。此外，设LP指标中可变参数α=0.5，RWR 指标中粒子返回概率c=0.1。由前文所述外生与内生因素接近性算法，进行链路预测，最终求得的预测精确度AUC如表2所示。

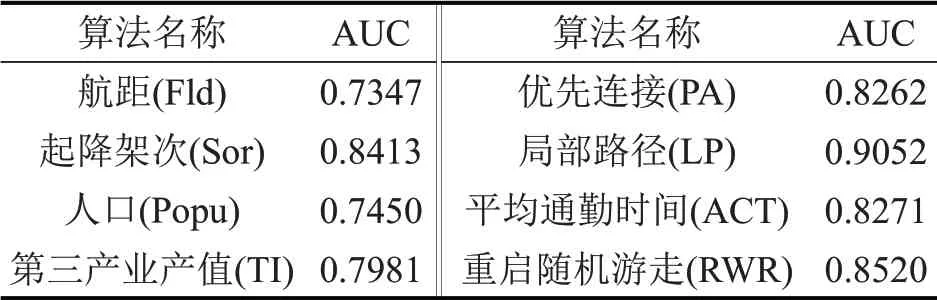
表2 8种接近性算法预测精确度Table 2 Prediction accuracy of eight proximity algorithms

由表2可以看出，在中小机场航线网络连接的外生影响因素中，机场的自身属性也就是起降架次的预测精确度值最高为0.8413，其次是机场所在城市的第三产业产值，预测精确度为0.7981。表明在中小机场航线网络中，机场的起降架次相较于其他外部因素是影响机场间是否连接的重要因素，机场自身因素对航线的连接决定性更大。此外，对4种内生因素而言，其接近性指标的预测精度均高于除起降架次以外的外生属性指标，其中基于局部路径的接近性预测精确度最高为0.9052。由于中小机场航线网络的结构特征不同于整体航线网络，其集聚系数较小使得从网络路径的角度进行链路预测更能符合网络的结构特征，同时基于随机游走过程的平均通勤时间与重启随机游走全局信息算法预测精确度也略好于局部信息优先连接算法，再次表明，网络路径的结构接近性更适合于中小机场航线网络的链路预测。总体来看，网络内生因素的结构接近性预测效果整体好于外生属性的接近性，从网络路径的角度进行预测效果较为理想，挖掘小机场网络内部的结构信息更有利于预测网络的连接情况。

3 接近性耦合算法及预测应用

3.1 接近性耦合算法

网络中节点的连接与否绝不是单个因素决定的，有必要进一步耦合不同类型的接近性，以综合分析网络的连接机制。考虑到内生因素的整体预测精确度好于外生属性，局部路径的接近性预测效果最好，而外生属性中起降架次的接近性预测精确度最好，因而本文在确定起降架次与局部路径接近性作为主要耦合因素的情况下，继续选择不同的内生因素接近性进行多因素耦合，表示为

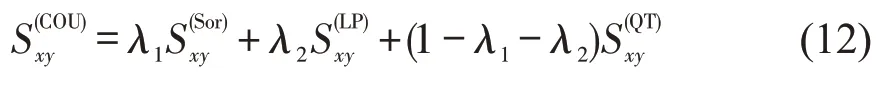
式中：为基于网络内生因素接近性的其他3 种指标的1 种；λ1，λ2为耦合系数，λ1、λ2∈[0,1]，且λ1+λ2≤1，任意λ1、λ2的取值步长为0.1。当任一λ1、λ2取值为1 时，耦合算法回归到系数取值为1的初始算法。为了确保耦合算法的合理性和准确性，各耦合指标的接近性矩阵参数均除以其最大值，即采取归一化措施后进行耦合计算。

多因素耦合算法的预测精确度如图2所示，不同子图展现了λ1、λ2取值变化对精确度变化的影响。对图2进行分析发现，在不同的λ1、λ2取值情况下，各耦合算法均存在最优值，图2(a)、(b)均在(λ1,λ2)=(0.1,0.9)时分别取得最优值0.90663、0.90609，而 Sor + LP + RWR 算法则在(λ1,λ2)=(0.0,0.6)取得最优值0.9088。具体来看，对Sor+LP+PA算法而言，在λ2取值一定的情况下，λ1取值越大时精确度越高；当λ2取值尽可能大，λ1取值尽可能小时，该耦合算法预测精确度越好，也就是精确度值整体受LP 接近性影响较大。对Sor+LP+ACT 算法而言，当λ2取值越大，λ1取值越小时，其耦合精确度越高且波动性越小，表明LP接近性在此耦合方式中具有主导性。对Sor+LP+RWR算法而言，其耦合最优值效果最好，但与Sor+LP+PA 算法精确度分布不同，在λ2取值一定的情况下，λ1的取值增加会使得预测精确度降低。总体来看，在不同λ1、λ2取值情况下，3 种耦合算法分别有98%、98%、95%的精确度值高于各自耦合方式中单个指标的最低值，说明耦合算法对预测精确度的提升效果较好，但在λ2取值为0 的11 种情况当中，3 种耦合算法的精确度均处于末位，整体与λ2存在取值时有着较大差距，随着LP接近性的加入，会使得各自精确度逐渐增加。为了进一步展示耦合算法的预测效果，对耦合算法预测效果与原单个算法进行比较，结果如表3所示。

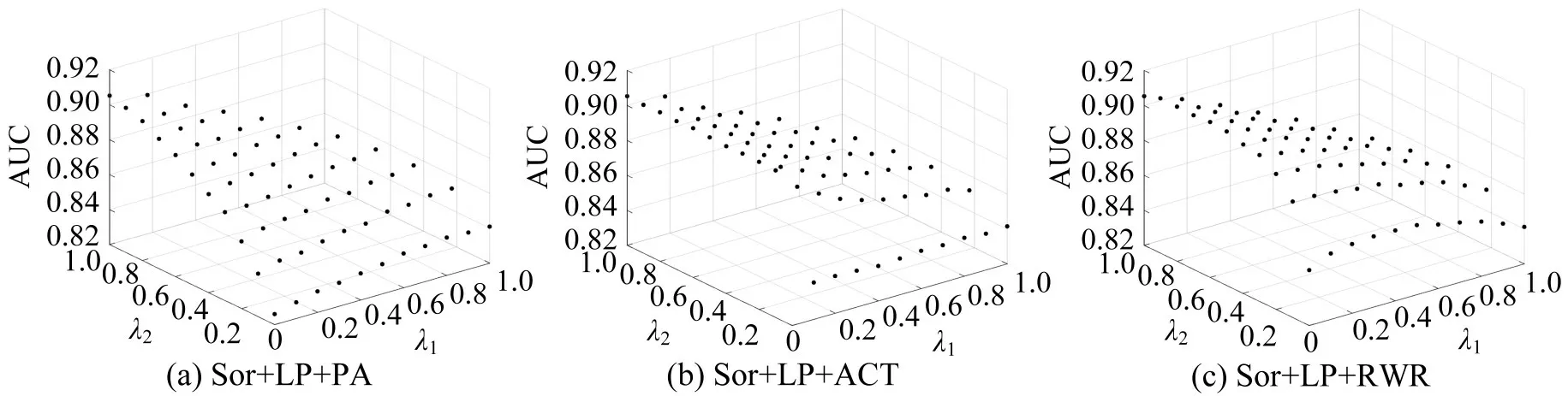
图2 耦合算法精确度变化情况Fig.2 Accuracy change of coupling algorithm

表3 耦合算法精确度统计Table 3 Accuracy statistics of coupling algorithm

由表3可以看出，耦合算法的精确度在各自耦合范围内均高于单个指标，但相较于LP 指标精确度则提升极其有限，此外当各耦合算法取得最优值时，λ2取值分别为0.9、0.9、0.6，可以看出LP指标在耦合算法中具有主导作用，这种单个指标在耦合算法中起主导作用的现象在我国整体航线网络[3]与能源供应链网络[7]中均有发现。尽管从精确度数值比较角度，所有耦合算法相较于LP指标提升不明显，但通过耦合方式对整体以及其他耦合指标精确度的提升效果不可忽视。在单个指标的精确度中，仅有LP指标达到0.9以上，但通过耦合以后，3种耦合算法达到0.9 以上的精确度的情况数量分别为5、19、20，同时上文也有提到所有耦合方式均有95%以上的精确度值高于单个指标的最低值，因此表明通过耦合的方式能提高对中小机场航线网络连接可能性的预测效果。

3.2 耦合算法预测结果应用

利用节点间接近性进行链路预测的一个前提是，节点间连接可能性越大则他们之间的接近性越高。在所有耦合算法当中，Sor+LP+RWR算法最优值较高，本文考虑以其取得最优值时的节点间接近性作为预测结果。将此时的接近性矩阵视为节点间的连接网络，得到50176 组节点间接近性值，对该网络进行无向化以及去除自环处理后，得到无向的航线网络全图，共24976组接近性值。由于航线网络边集满足于E=ET∪EP，但在该预测情况下，边集E的各边接近性值处于整体排序的前列。一个直观的现象是，在接近性排序较高的前400条航线中，仅有9.25%的航线不属于边集E，这些航线也就是不存在的航线。若不存在的航线接近性值排序越靠前且高于已经存在的航线，则表明该航线的两机场间具有很大的连接可能性。在接近性值排序中，有2407条航线接近性值高于0.1，在整体排序中属于连接可能性较大的航线，排除已经存在于边集E的1290 条航线以及40 条非中小机场航线后，共得到1077条不存在的中小机场航线，本文以该1077条连接可能性较强的航线作为预测航线。

对预测航线的地理空间分布进行分析发现，所预测的航线主要集中在东部地区，内陆的机场倾向于连接沿海地区机场。其中大多数中小机场预测连接的对象均为省会或区域中心城市，中小机场间的连接依然较少。同时，预测结果也显示在西北地区的中小机场与内陆连接可能性较小，这是由于连接中小机场的航线一般为中短程航线，地理距离的存在使得其新增航线连接受限，以上预测现象也较为符合中小机场的实际连接情况。

当然，预测结果的好坏也离不开实际的检验，本文将预测结果与2020年、2021年夏秋航季的中小机场航线进行对比，并计算了两个年度实际新增航线的接近性值，得出相对于2019年的接近性值环比增长情况，如表4所示。2020年、2021年相较于2019年中小机场航线数量有所增加，实际新增航线数量变化较大，分别为431 条和674 条。对于命中的航线而言，其在两个年度的实际新增航线中的占比(命中率)均达到1/3以上，2020年、2021年命中航线的接近性值相对于2019年平均增长率分别为55.4%、39.6%。对于未命中的航线而言，2020年、2021年分别有265条、428条航线的接近性值相较于2019年大幅增长，各自的平均增长率均达到300%以上，也就是这些航线的接近性值增长达到2019年的3倍以上，造成此现象的原因可能是这些航线连接的机场在2019年之后的网络演化当中结构特征变化较大，如路径数量增加、连接机场数增多等，最终影响了航线的接近性值变化。此外，相较于2019年航线的接近性值，2020年、2021年未命中航线中分别有10 条、14 条航线的接近性值降低1%左右，这类航线在未命中航线当中占比极少且变化很小。对比命中航线及未命中航线的接近性值平均增长情况可以发现，2020年、2021年命中航线的接近性值平均增长率较小，也就是命中航线连接机场的结构特征较为稳定，而未命中航线的接近性值平均增长率极大，表明在新增航线预测工作当中机场节点的路径及连接变化等情况会极大的影响预测命中效果。当然，由于2020年新冠疫情的爆发，疫情防控政策和航空市场低迷导致大量的国际航线停飞，航空公司将运力转移到国内航空市场，国内航空市场受疫情防控政策影响较大，从而对新增航线的预测也产生一定影响，但以上结果仍然表明耦合算法能一定程度模拟中小机场航线网络连接机制，具有一定实用性。

表4 预测结果对比统计Table 4 Comparative statistics of prediction results

4 结论

本文使用链路预测方法，探索不同属性或因素对中小机场航线连接影响的程度并进行验证，得到的主要结论如下：

(1)在单个接近性指标中，中小机场的起降架次在外生属性中预测效果最好，机场自身的因素对航线连接影响较大，航距、人口等环境因素则影响相对较小，而基于网络路径的LP 指标在所有内生因素中精确度最高，网络集聚程度较低使得网络路径的构成会极大影响节点连接情况。同时内生因素指标的预测精度均高于除起降架次以外的外生属性指标，相较于中小机场网络的外部因素，挖掘其网络内部的结构信息更能预测网络的连接情况。

(2)从多因素耦合算法预测精确度来看，耦合网络内外因素的预测效果优于单个指标，LP 指标在耦合算法中占主导地位，通过耦合的方式能提高中小机场航线网络连接预测的精确度。

(3)预测的中小机场航线主要集中在东部地区，多数中小机场依然选择省会或区域中心城市连接，所预测的航线在后两年的新增航线中占比均高于1/3，命中航线的接近性值变化相对较小，网络结构演化的稳定性对预测结果有较大影响。