电动自行车与机动车事故严重性影响因素分析

马景峰，任刚，李豪杰，曹奇，杜建玮

(东南大学，交通学院，南京 211189)

0 引言

近年来，伴随人们的出行需求快速增大，电动自行车与机动车保有量急剧增加，日趋严重的交通拥堵已成为城市通病之一[1]。作为一种非常重要的出行工具，电动自行车因具有省力快速、灵活便捷、高效实用及廉价环保等诸多优势而广受中、短距离出行者的青睐[2]。目前，我国电动自行车保有量已超过3亿辆，在不同经济发展水平的城市道路交通系统中均有着举足轻重的地位。但由于电动自行车具有相对高速性、较大灵活性、管控不便性及干扰敏感性等特征，且其违规行为成本较低，骑行者安全防护装备较差，导致电动自行车事故频发，其交通安全问题日趋严重[3]。此外，电动自行车与机动车经常共享同车道混行权，导致交通秩序变差，既降低了通行效率，更造成了电动自行车与机动车碰撞事故频发，其导致的生命与经济损失比其他类型的电动自行车事故(侧翻或与自行车、人及固定物碰撞事故)更加巨大[4]。为缓解城市电动自行车与机动车事故危害，亟需定量分析各潜在因素对该类事故严重性的差异性影响[5]。

围绕电动自行车交通事故的建模分析，一直广受国内外学者关注。XING等[6]利用广义线性模型(Generalized Linear Model,GLM)，探索时空、环境及骑行者属性等因素对北京市电动自行车与人力自行车事故严重性的影响；YU等[7]提出广义估计方程(Generalized Estimating Equation,GEE)研究风险感知、责任感及骑行者年龄等因素对电动自行车与行人事故的影响；BIGAZZI 等[8]构建结构方程模型(Structural Equation Model,SEM)计算能量排放、空气质量与电动自行车事故的关系；李英帅等[3]建立了随机森林模型(Random Forest Model,RFM)，剖析碰撞类型、事故时间、道路条件、骑行者与驾驶员信息以及车辆类型对电动自行车与机动车事故严重程度的影响；周继彪等[5]基于问卷数据，以二项(Binary)probit 模型量化了骑行者属性(性别、年龄、职业、收入、受教育程度等)、危险感知度、节日类型及车牌使用等因素对电动自行车事故的影响；MA等[9]同样利用二项probit 模型，厘清冒险驾驶行为对城区电动自行车与机动车事故严重程度的影响差异性；YUAN 等[10]提出二项(Binary)Logit 模型研究时空、道路环境及骑行者信息等因素如何影响电动自行车与机动车事故；DU 等[11]考虑事故多分类本质特性，利用多项Logit(Multinomial Logit,MNL)模型量化分析了时空与骑行者信息对电动自行车事故的影响，但该模型要求各自变量需要保持彼此独立性，即严格遵守IIA(Independence from Irrelevant Alternative)特性；XU 等[12]通过建立混合(Mixed)Logit 模型，松弛了IIA 特性，研究超速行为与限速设置对电动自行车事故的影响；GUO等[13]构建贝叶斯(Bayes)Logit 模型，计算时空、道路条件、闯红灯行为、车型及骑行者属性等因素对电动自行车事故的影响。

以上有关电动自行车事故研究所用的模型或方法均为无序反应模型，为了贴合事故严重性的有序多分类特性，一些学者提出了有序反应模型。WANG 等[14]构建有序Logit(Ordered Logit,OL)模型，研究骑行者对交通规则熟悉度与头盔使用行为对电动自行车交通事故的影响，但该模型要求自变量都严格遵守平行线(Parallel-lines Assumption,PL)假设，即自变量回归系数不随事故严重性变化而变化；为了松弛PL 假设，WANG 等[15]提出广义有序Logit(Generalized Ordered Logit,GOL)模型，允许所有自变量违背该假设，定量分析时空、道路、环境及骑者信息如何影响电动自行车事故严重程度。

此外，一些学者建立支持向量机(Support Vector Machine,SVM)[16]、灰色马尔科夫(Grey Markov,GM)[17]或神经网络(Neural Network,NN)[18]等模型预测交通事故严重性或数量，但这些分类预测模型以预测精度为目标，对事故影响因素可解释性较差；也有部分学者采用巢式(Nested)Logit 模型[19]，通过松弛IIA 特性，分析交通事故影响因素，但该模型为无序反应模型，不能体现部分影响因素的有序本质与交通事故严重程度之间的内在联系。

关于电动自行车交通事故的研究，综上可知：①在研究对象方面，主要聚焦于电动自行车与慢行事故研究(自行车或行人)、电动自行车违章行为分析(超速、闯红灯等)及电动自行车能耗对环境影响等，而针对电动自行车与机动车的研究不足，其严重性影响因素定量分析更为匮乏；②在影响因素选择方面，主要考虑时间、空间、道路、环境、骑行者及车辆属性等因素中的部分因素，缺少对这6类因素同时定量研究；③在模型应用方面，主要分为无序模型与有序模型两类，例如，多项Logit模型等无序模型，要求自变量遵守IIA特性，虽然有序模型既能体现分类变量的有序本质，但其中有序Logit模型要求所有自变量严格遵守PL 假设，而广义有序Logit模型中，所有自变量均不受该假设限制，两者均缺乏灵活性。

作为有序Logit 模型与广义有序Logit 模型的综合改进模型，偏比例优势(Partial Proportional Odds,PPO)模型在充分体现各分类变量有序特性的同时，允许部分变量违背PL假设，而部分变量遵守该假设，故其具有更强的灵活性，因此，非常适用于有序多分类变量研究[20]。目前，鲜有学者采用PPO 模型进行电动自行车与机动车事故严重性影响因素分析。

本文以2018年1～12月绍兴市上虞区交通局电警系统中记录的10304 起电动自行车与机动车事故为数据支撑，在剖析其严重性分布与时空分布特性基础上，选取6类影响因素，利用MNL、OL、GOL及PPO模型进行拟合对比分析，进而结合最优模型(PPO模型)与边际效应量化分析事故严重性影响因素，并根据各因素的影响差异性提出相关管理建议，可为电动自行车交通安全管理者的精细化管控决策提供有效支撑。

1 电动自行车与机动车事故特性分析

1.1 事故严重性分析

事故严重性影响因素选取与模型应用等方面，电动自行车交通事故的研究情况如表1所示。

表1 电动自行车交通事故研究Table 1 Research on E-bicycle crashes

根据现有大多数研究中对电动自行车事故严重性的分类方法，本文将电动自行车与机动车事故严重程度用j表示，j=1 为未受伤(仅经济损失)，j=2 为轻伤，j=3 为重伤(包括致命事故)。统计分析绍兴市上虞区交通局电警系统中2018年10304起电动自行车与机动车事故，未受伤、轻伤及重伤事故数依次为：3190，4240，2874起，其占比依次为：31.0%，41.1%，27.9%。

电动自行车与机动车事故严重性影响分析具有多维度复杂性，本文从时间、空间、道路、环境、骑行者及车辆属性这6方面，选取17个因素进行影响分析，各变量在不同严重程度的统计特性如表2所示。其中，车流相交角为事故发生时机动车行车方向与电动自行车行车方向的交叉角度，慢行交通由行人、人力自行车及电动自行车(两轮、三轮)组成。

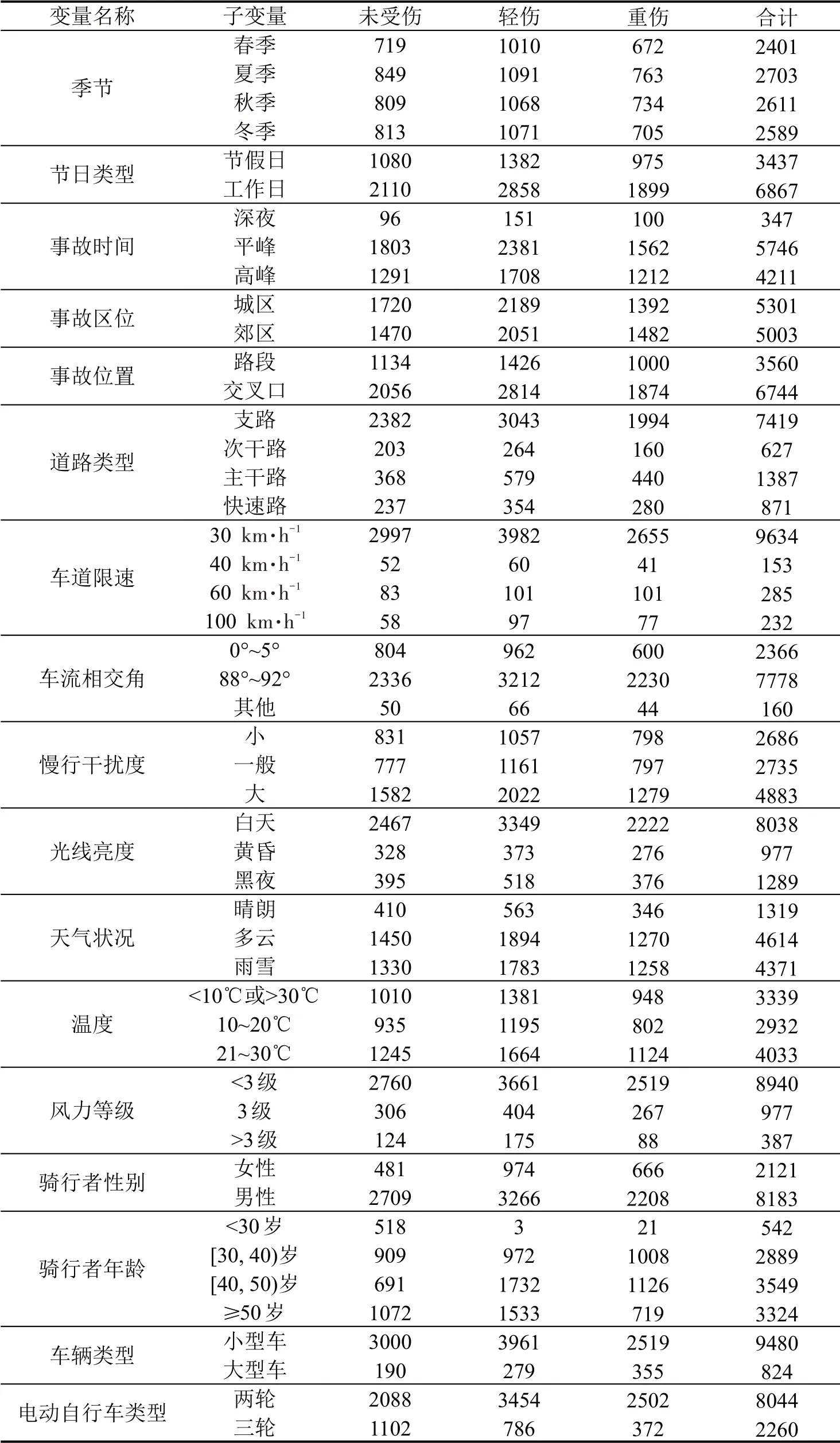
表2 变量分类、编码及频数Table 2 Classification,coding and frequency of variables

1.2 时间特性分析

所选事故频数(单位：起)的月份(季度)分布与小时分布如图1所示。由图1事故的月份(季度)分布可知：该地电动自行车与机动车事故的不同月度的24 h 频数分布规律基本一致，即均呈现“双高峰”；2018年月均859 起事故，事故数最高的前4 个月份依次是春季4月、夏季7月、冬季12月与秋季9月，其事故数均不少于900起；2月由于春节节假日的存在，居民出行需求下降，出行率明显降低，交通冲突几率随之降低，故日均事故数显著少于其余月份。

此外，由表2可知，夏季的电动自行车与机动车事故数最多(2703起)，可能是因为夏季天气比较炎热，而电动自行车骑行者对其感受非常敏感，为追求出行舒适感而提高骑速，以致提高了事故概率；其次是秋季与冬季，而春季事故数明显少于其他3个季节，且在不同事故严重程度上也基本符合季度性排序规律，但春季四月份事故总数(966 起)与日均事故数32.2 起·d-1均明显高于其他月份，这与上虞区当地气候特征密切相关，2018年4月上虞区超过2/3时间为阴雨天气。

由图1事故的小时分布特性可知，该地电动自行车与机动车事故在同一日内小时频数分布存在明显的双峰波动性，但每月的事故数日分布规律基本保持一致(2月高峰期略有差异)，这与当地交通量时间分布规律保持一致，即事故数与交通量或交通密度基本呈正相关。据此，本文将事故时间变量划分为3类：深夜(晚22:00-次日6:00)、高峰(7:00-9:00 与16:00-18:00，2月高峰时段为10:00-12:00 与13:00-15:00)及平峰(剩余时段)。不同严重程度下该类事故小时分布情况如图2所示。

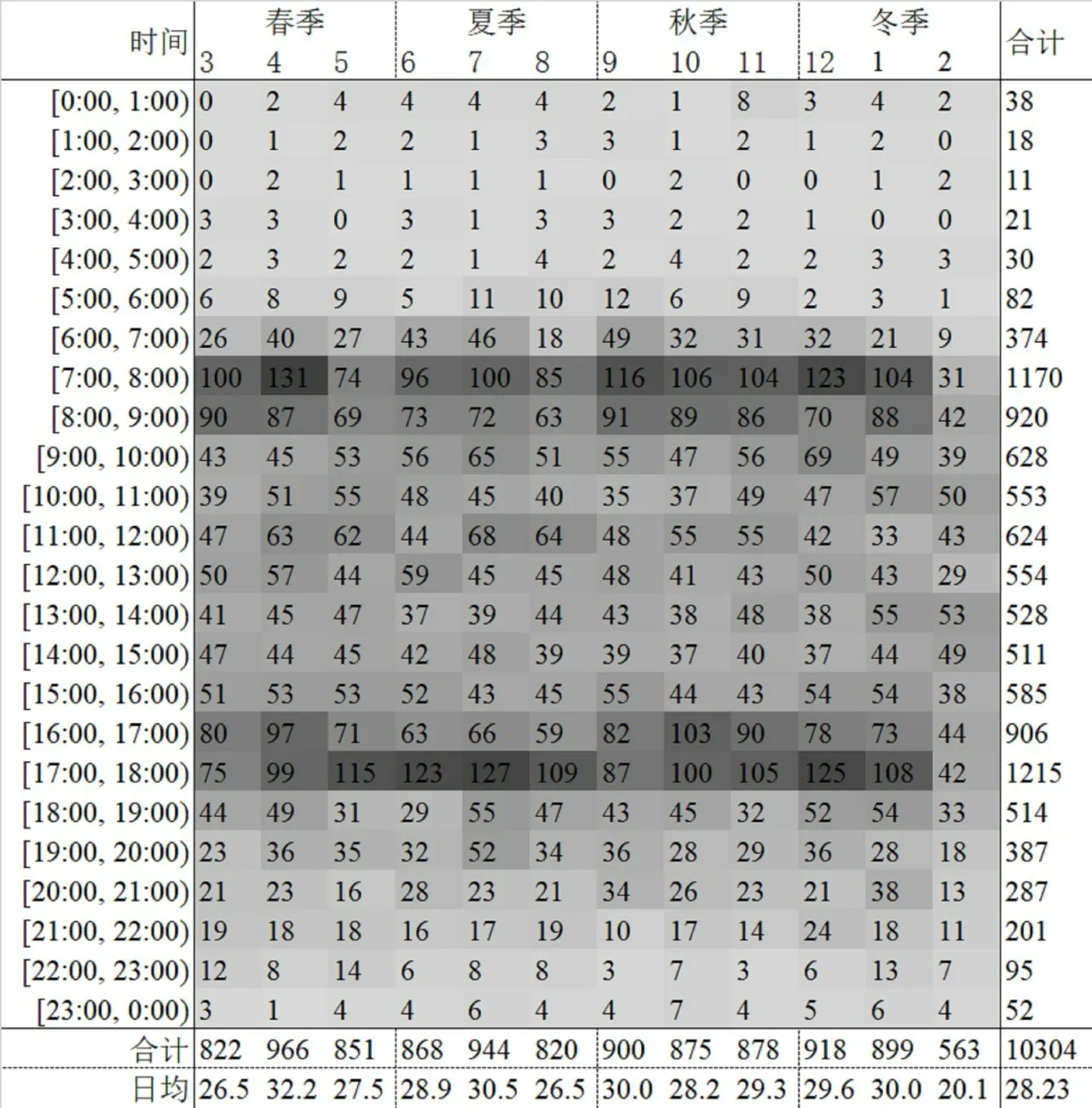
图1 事故频数小时-月份分布Fig.1 Frequency distribution of crashes by hour and month

由图2可知，不同严重性事故的24 h频数分布规律基本一致，即[7:00,8:00)、[17:00,18:00)为最明显的事故双高峰；[11:00,12:00)为事故次高峰，此时间分布特征可为交通安全管理部门进行主动防控与警力部署提供一定的决策依据。

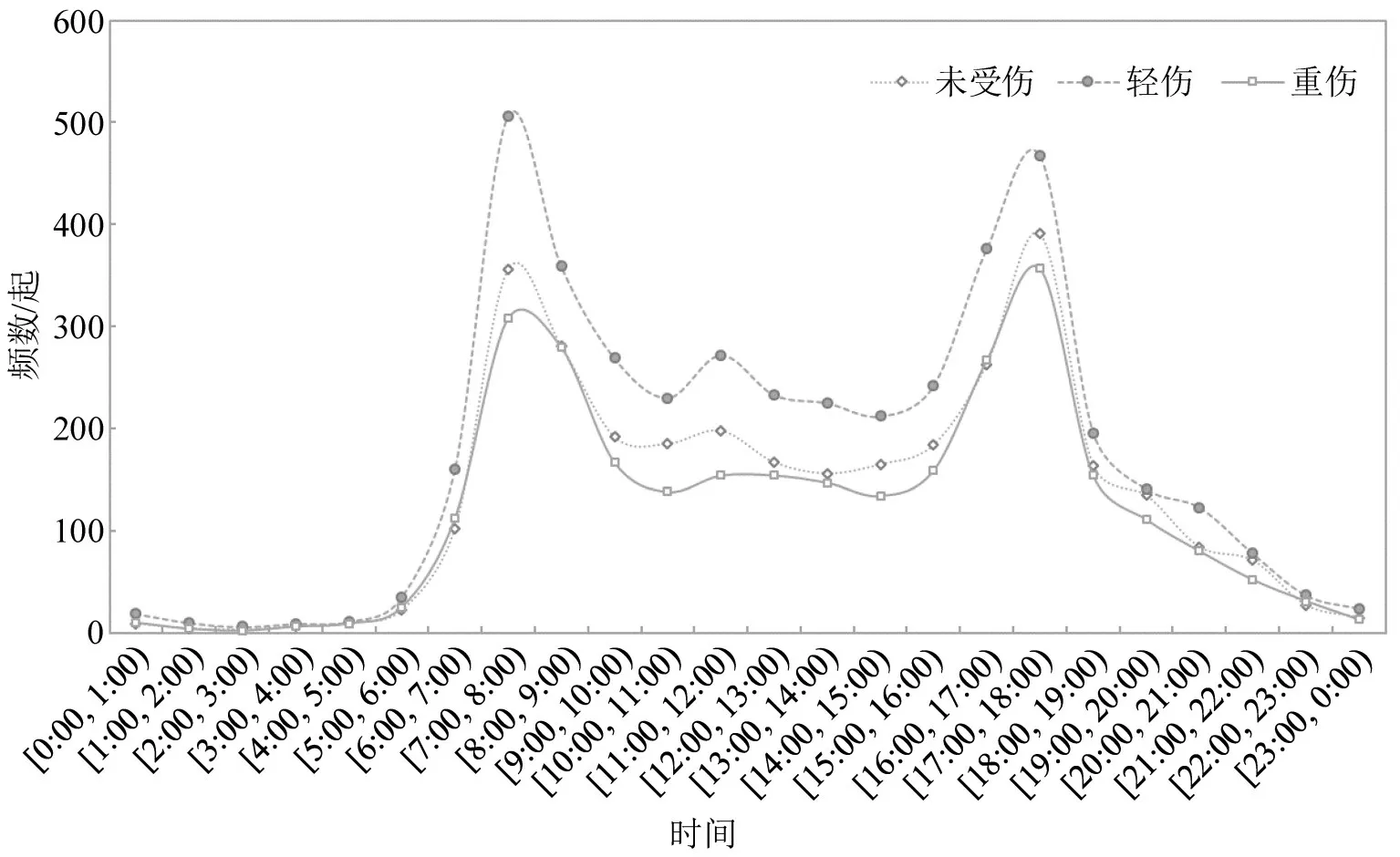
图2 事故频数小时-严重程度分布Fig.2 Frequency distribution of crashes by hour and severity

该类事故的不同节日类型的日均-小时分布情况如图3所示。由图3可知，节假日与工作日的24 h波动规律基本一致，两者日均事故数每小时最大值不超过4起，且[20:00，次日6:00)时段内日均事故数均不到1 起；[7:00,8:00)和[17:00,18:00)同样为两类节日中最明显的事故双高峰，[11:00,12:00)是事故次高峰；虽然节假日与工作日的日均事故数分别为28.40 起和28.14 起，即前者整体上大于后者，但是[6:00,9:00)和[16:00,18:00)两个时段内节假日事故数却小于工作日，这与此时段内工作日所具有的大流量和高密度的通勤交通时间分布规律密切相关。

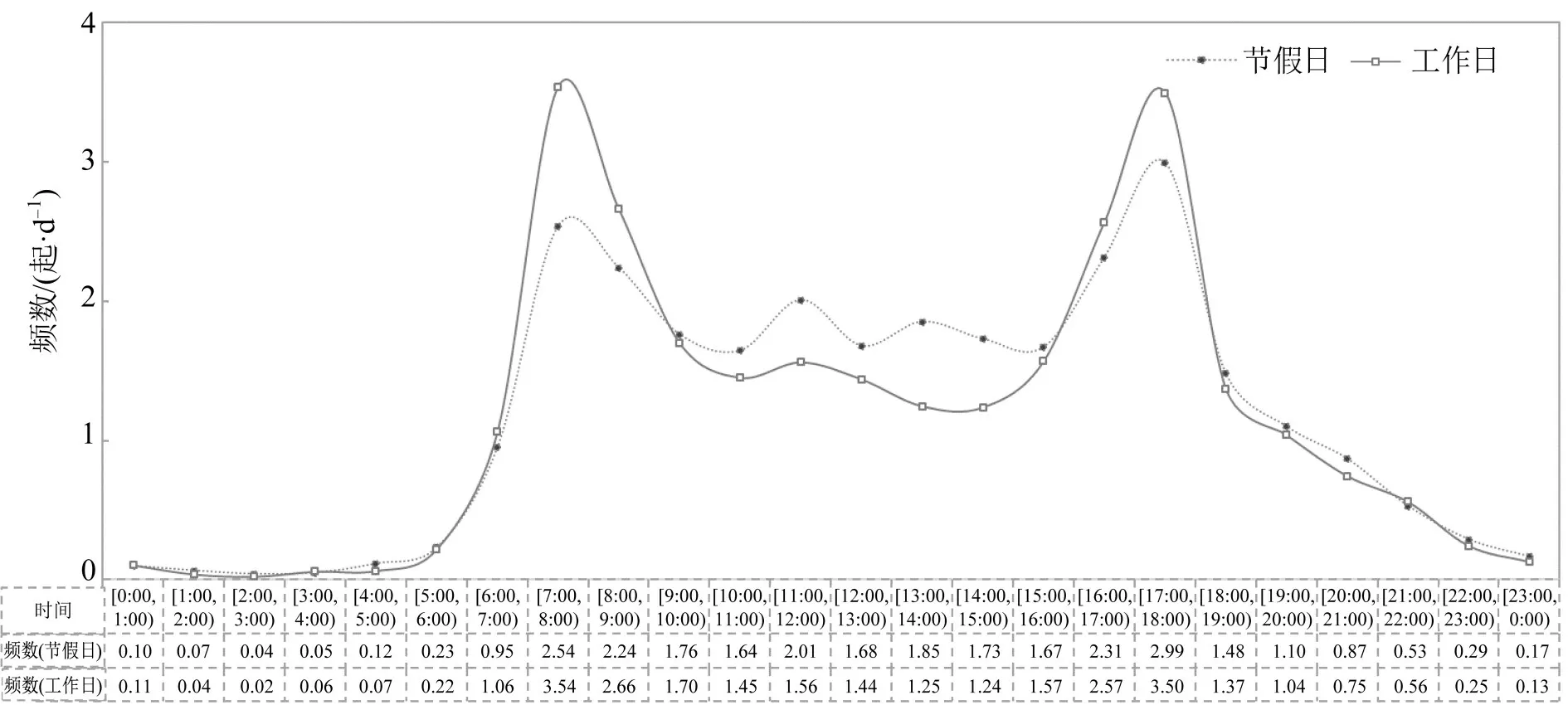
图3 不同节日类型的日均-小时事故频数分布Fig.3 Frequency distribution of crashes by average hour and day

1.3 空间特性分析

对所选的电动自行车与机动车事故数据进行空间特性分析，得到该事故频数的区位、位置及道路类型分布如图4所示。

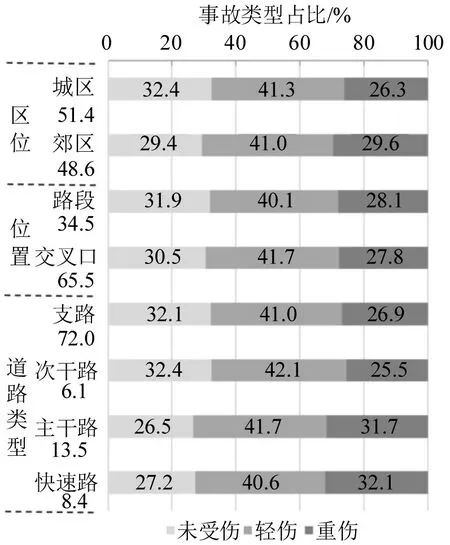
图4 电动自行车事故空间分布Fig.4 Spatial distribution of e-bicycle crashes

①从事故区位分布来看，城区与郊区电动自行车与机动车事故数相近(城区5301起，郊区5003起)，但两者在不同严重程度上的分布规律存在一定的差异性。此外，上虞区总面积1403 km2，其中，城区和郊区占地分别为37.80 km2，1365.20 km2，则两者的年均电动自行车-机动车事故率分别为140.24，3.66 起·km-2，即前者是后者的38.32倍，具有显著的差异。这与两者的人口密度、路网密度、交通密度、冲突密度、管控设备布设密度、服务水平及用地情况等指标密切相关。

②从事故位置分布来看，交叉口处与路段上发生的电动自行车与机动车事故频数差距较大(交叉口6744 起，路段3560 起)，即前者是后者的1.89倍。因为前者比后者交通流复杂度大很多，交通冲突更为频繁。但是，两者在不同严重程度上的事故占比分布规律差异性不大，交叉口因为具有限速偏低、车流稳定、监管设备密度大及交通参与者更谨慎等特性，导致其轻伤事故占比大于路段，而路段由于具有限速偏高、车流不稳定及机非混行频繁等特征，导致其未受伤与重伤事故占比大于交叉口。

③从道路类型分布来看，支路上电动自行车与机动车事故数(7419 起)明显大于其余3 类道路：次干路627起，主干路1387起，快速路(本文指快速道路辅路)871起，即前者是后者的5.35倍以上。因为，城市支路总里程与总通行量较大，且其以生活功能为主，监控设备部署密度较低，慢行交通量较大，交通秩序较差，电动自行车与机动车混行现象较多，交通环境更为复杂，且交通冲突更为频繁。此外，4 类道路在不同严重程度上的分布规律也存在较大的差异性。

2 分析方法

2.1 模型构建

本文建立多项Logit 模型(MNL 模型)、有序Logit 模型(OL 模型)、广义有序Logit 模型(GOL 模型)及偏比例优势模型(PPO模型)。其中，PPO模型既能够反映各变量的有序本质，又允许部分自变量的系数随不同水平等级的不同而存在差异性，具有较强灵活性。PPO 是有序Logit 模型与广义有序Logit模型的改进模型。

(1)多项Logit模型

MNL模型严格遵守IIA特性，其概率计算表达式为

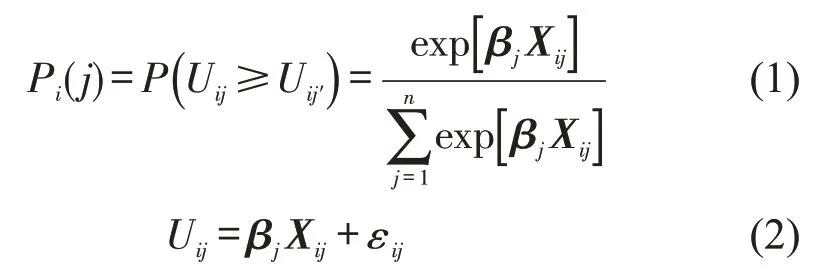
式中：j为事故严重程度；n为因变量分类数目；Uij为决定对象i水平等级j的函数；Uij′为对象i水平等级j的具体值；Xij为研究对象i水平等级j的向量；βj为自变量水平等级j回归系数向量；εij为随机误差项。

(2)有序Logit模型

OL模型中变量都严格遵守PL假设，其概率计算表达式为

式中：Yi为对象i的严重性等级；Xi为事故i的向量；β为自变量回归系数向量；τj为第j严重程度的常数项。β和τj可由极大似然法得出。

(3)广义有序Logit模型

GOL 模型中变量均违反PL 假设，其概率计算表达式为

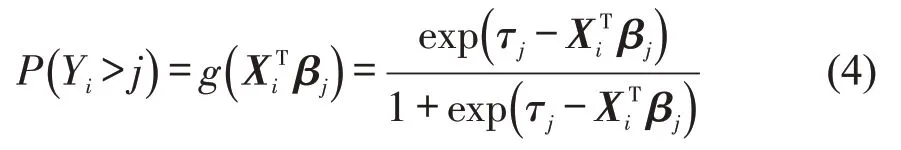
(4)偏比例优势模型

PPO模型中通过引入γ参数，允许部分变量满足PL假设，而其余变量违背该假设，相比前3个计量经济模型，该模型具有更强的适应性与灵活性，其概率计算表达式为

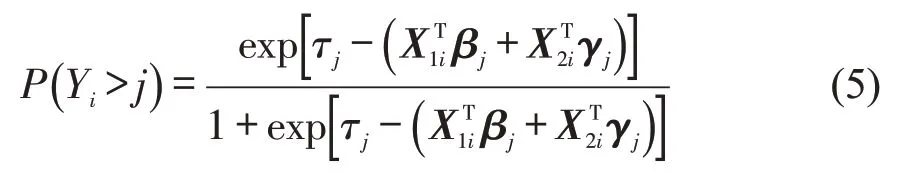
式中：X1i为遵守PL 假设的自变量向量；与其对应的回归系数向量为βj；X2i为不受PL 假设限制的自变量向量，与其对应的回归系数偏差向量为γj。

2.2 边际效应

边际效应可用于定量分析不同因素对因变量影响的强弱程度与变化趋势，其表达式为

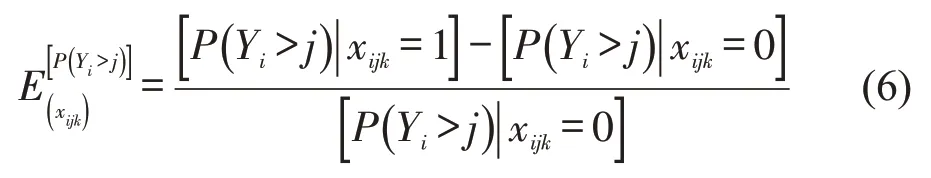
式中：为事故i的第k个变量在第j严重性的自变量xijk的边际效应值。

2.3 模型对比

采用AIC 与BIC 信息准则，对比MNL、OL、GOL、PPO模型的拟合优度，EAIC与EBIC值越小，则模型拟合效果越好。

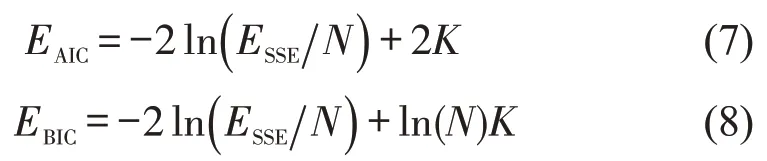
式中：ESSE为误差平方和；N为电动自行车与机动车事故数；K为模型中待估计的参数数目；令

3 模型分析

3.1 模型对比分析

利用STATA15.0 软件，分别设计MNL、OL、GOL及PPO模型的求解算法，分析所选的10304起电动自行车与机动车事故数据，得到各模型拟合参数如表3所示。

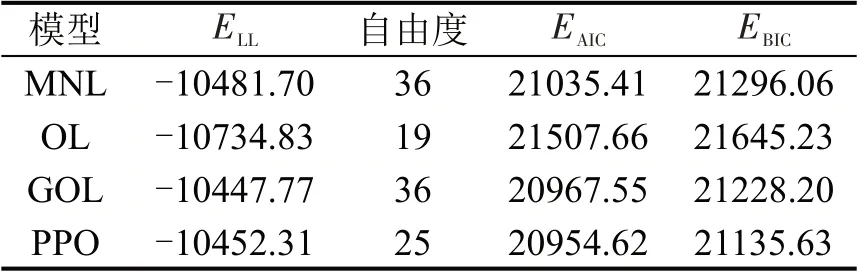
表3 拟合优度检验Table 3 Test of goodness-of-fit

由表3可知，PPO模型的EAIC与EBIC值均最小，则其拟合效果最佳，故以PPO模型及其边际效应做进一步量化分析。

3.2 偏比例优势模型结果分析

应用PPO 模型对所选交通事故数据进行gologit2算法求解，得到参数估计结果如表4所示。

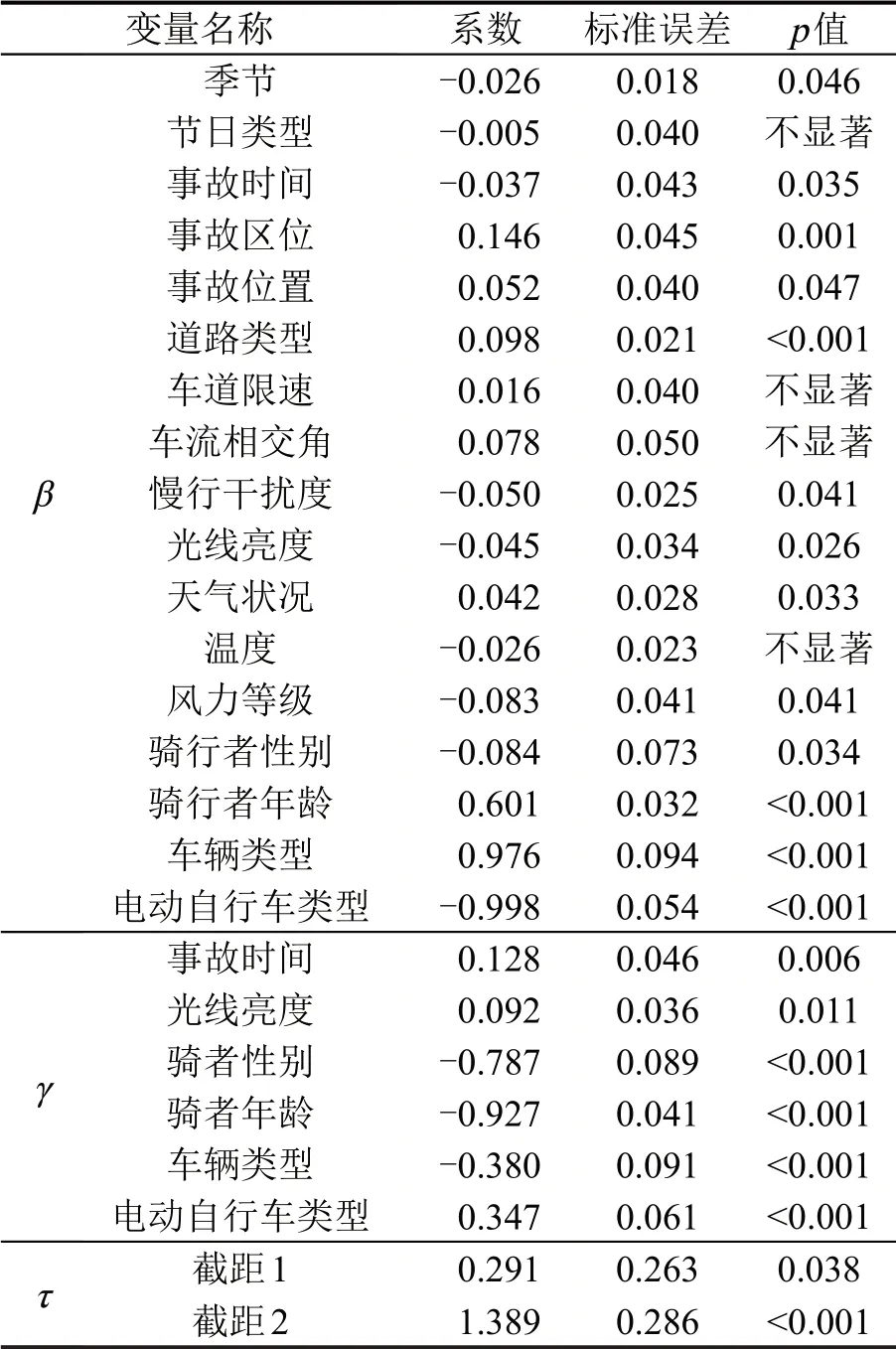
表4 偏比例优势模型参数估计Table 4 Parameter estimation for PPO model

由表4可知，除节日类型、车道限速、车流相交角及温度这4 个因素对电动自行车与机动车事故严重性影响不显著外，其余13 个因素均有着显著影响。此外，由γ参数计算结果可知，事故时间、光线亮度、骑者性别、骑者年龄、车辆类型及电动自行车类型这6个变量都不遵守PL假设，其余7个显著影响因素均满足该假设。

为量化分析各变量间与变量内对该类事故严重程度的影响差异性，需对各显著影响因素进行边际效应分析，其结果如表5所示。由表5可知，各影响因素间有着较大差异性影响：

①对于电动自行车与机动车事故严重性影响最大的前4个显著因素为电动自行车类型、车辆类型、骑行者年龄及性别，其边际效应绝对值最大值均超过51%，表明该类事故严重程度对事故碰撞对象与交通参与者的差异性最为敏感，因为两者均是事故产生的直接主导型承担者。

②事故区位、道路类型及光线亮度的影响一般，其边际效应绝对值最大值在20%～30%，表明道路条件与行车视距对事故严重性也有较大影响。

③事故时间与风力等级的影响较小，其边际效应绝对值最大值在10%～20%，因为不同事故时间的道路交通流密度与交通复杂性存在较大差异，两者都是能够直接影响到电动自行车与机动车的通行环境与交通参与者驾驶行为的动态外部因素，而风力等级虽然对机动车及驾驶员影响教小，但对电动自行车及骑行者均影响极大。

④季节、事故位置、慢行干扰度及天气状况的影响最小，虽然其边际效应均不超过8%，但是交通条件与气候环境对该类事故严重程度均有着不可忽视的显著性影响。

此外，由表5可知，不同影响因素内部的不同子分类之间对该类事故严重程度也存在着较大差异的影响。

表5 偏比例优势模型的自变量边际效应Table 5 Marginal effects of independent variables in PPO model

(1)时间影响分析

①4 个季节对不同严重程度的电动自行车与机动车事故影响趋势比较一致，但影响幅度差异性比较明显，其中，冬季影响最大，春季影响最小，因为与其他季节相比，冬季的不利气候发生率更高，通行视线更差，可视距离更短，对路面条件与骑行者均会产生极大的不利影响，事故概率更大，但是，恶化的交通环境与道路条件导致骑行者与驾驶员注意力更加集中谨慎，车速更低，受伤事故概率更低，可根据季节差异性影响力合理调整外勤警力部署方案与路面修养工作。

②在事故时间方面，与深夜时段相比，高峰对不同事故严重程度的影响均显著大于平峰(近2倍)，两者均会造成未受伤与重伤事故概率的增加，因为，不同时段的交通状态存在较大差异性与规律性，交通事故概率与交通冲突点密度呈正相关，而交通冲突点密度又与道路交通流密度呈正相关，与交通服务水平呈负相关，因此，从深夜到平峰，再到高峰阶段，未受伤事故概率随交通密度增加而增大，重伤事故概率随交通流量增大而增大，但轻伤事故概率随运行车速降低，随车流趋于稳定而减小，因此，管理部门可提倡灵活有效的缓解策略或措施，例如，错峰出行、诱导出行及区域微循环等。

(2)空间影响分析

①在事故区位方面，郊区对事故严重性影响比城区明显大(近2倍)，与城区相比，郊区会造成未受伤概率的降低(11.28%)，而重伤事故和轻伤事故概率分别增加10.34%、0.94%，因为，郊区道路监管设备密度低，交警警力投入少，交通干扰少，导致机动车与电动自行车的整体行车速度高于城区，并且郊区路面障碍物清除不够及时，道路标志标线、照明及辅助服务设施布设质量差和密度低，所以，郊区事故一旦发生，通常更为严重，可根据区位差异性需求分析合理布设道路监管和辅助设备密度与质量。

②在事故位置方面，与路段相比，交叉口对不同事故严重性影响更大，会造成未受伤事故概率降低3.18%，而重伤事故概率增加3.21%，因为，交叉口通常比路段管控设备更齐全，交通干扰更多，交通环境更复杂，驾驶员与骑行者更为专注谨慎，机动车与电动自行车运行速度更低，导致未受伤事故概率降低，但交叉口处会有部分闯红灯违章事件发生，特别是在夜间或者郊区的交叉口，比路段的冲突更多且更激烈，因此，重伤事故概率更大，据此不仅要注意路段交通管控，更应优化交叉口渠化设计，增强交通监管与违章惩治力度，在提高交叉口通行效率的同时，要注重提升交叉口安全水平等。

(3)道路影响分析

①在道路类型方面，与支路对事故严重性影响相比，道路等级越高，影响力越大，特别是主干路与快速路，导致未受伤事故概率降低14.31%和21.99%，而重伤事故概率增加13.78%和20.06%，这与不同等级道路的功能差异性、交通复杂性及结构多样性等密切相关，道路等级越低，尤其在城区，道路越以生活功能为主，交通密度越大，混行越严重，轻伤或未受伤事故概率越高，但是，在高等级道路上由于车速较快，则重伤事故发生概率更高，可根据不同道路的影响差异与功能定位制定针对性的管控措施。

②与慢行干扰度小的地方(路段)相比，干扰度越大影响越大，一般干扰性(信控交叉口处)与较大干扰性(无信号交叉口或学校、医院等特殊出入口处)由于交通干扰多，交通参与者更加谨慎小心，车速下降，形成未受伤事故概率降低，但由于易受伤群体密度增大，导致重伤事故概率增大，因此，需要增强道路管控水平，实现密集型冲突集的时空隔离(机非隔离栏，增加信号灯等)，以提升道路安全性。

(4)环境影响分析

①在光线亮度方面，亮度越差对事故严重性影响越大，特别是与白天相比，黑夜里虽然由于交通量降低和冲突点减少而导致轻伤事故概率下降了22.03%，但是，因为交通视线较差和车流不稳定而导致未受伤与重伤事故概率分别增大15.86%和6.16%，表明道路环境中光线变差时，事故一旦发生就容易导致重伤事故，建议合理控制路灯照明时间与光照强度，增加光感和声控智能化路灯装置，及时维修故障路灯，或为相关标志标线添加新型光感材料。

②在天气状况方面，与晴天相比，多云与雨雪天气对不同事故严重性影响趋势比较一致，因为，交通参与者更加谨慎而未受伤事故概率分别下降3.02%和6.12%，轻伤事故概率下降幅度相近，但由于通行视线变差和地面摩擦力减小而导致重伤事故概率分别增加3.17%和6.26%。天气类型的影响幅度差异性比较明显，天气越恶劣，路面条件越差，对受伤事故影响越明显，因此，需要参考天气预报与实时天气变化进行精细化交通管控，多渠道提醒出行者选择出行方式，预先提高安全防护意识，交叉口处增设慢行遮阳挡雨棚，特别是事故多发地要强化管控手段，增加通行可视性。

③在风力等级方面，与小于3级相比，3级与大于3级的风对不同事故严重性影响趋势保持一致，未受伤事故概率分别上升6.02%和11.72%，但重伤事故概率却降低6.53%和13.34%，影响幅度存在明显差异，因为，风力属于不利外部因素，电动自行车骑行者对风力感受比较敏感，会增大未受伤事故概率，但是，风力的增强会迫使骑行者保持高度紧张状态而降低骑速，所以，受伤事故概率会降低。

(5)骑行者影响分析

①在骑行者性别方面，与女性相比，男性骑行者会增加14.90%的未受伤事故概率和9.48%轻伤事故概率，但会降低24.38%重伤事故概率，因为，男性比女性遇到突发交通情况更加镇定自若，且驾驶操作更擅于技术性与灵活性，所以，严重受伤事故概率会降低，但也因为男性交通参与者有着较强的炫技与高速心理需求和较为激进的驾驶风格与过多的驾驶技术自信，会增大未受伤事故的频数与概率。

②在骑行者年龄方面，与30岁以下的年轻人相比，年纪越大的骑行者驾驶经验越丰富，安全意识更高，出行时更有耐心，通常更能避免未受伤事故的发生，但是，由于年长者身体机能逐渐弱化和对于突发事件的反应速度变慢，灵活性较差，易引发更高概率的轻伤事故，但由于年长者(老人除外)对于出行更有耐心，骑车行为更稳重，更懂得避让机动车，尽量避免与机动车近距离混行，且骑速较低，所以，重伤事故概率略有所下降，可根据年龄的事故差异性影响与生活娱乐偏好行为，进行多样化交通安全文明出行宣传或交通突发事故应急行为教育。

(6)车型影响分析

①在机动车类型方面，与小型车相比，大型车因为流量小和密度低，与电动自行车交通冲突概率低，导致未受伤事故概率分别降低15.25%，但因为大型车灵活性较差、动能更大及减速度较小，而导致轻伤与重伤事故概率增大1.84%和13.41%，所以，通常大型车事故频数较低，但一旦发生事故就容易造成更严重的生命或财产损失，因此，要科学进行车道功能划分，合理进行车种限行管理及增设机非隔离栏。

②在电动自行车类型方面，与两轮车相比，三轮电动自行车由于其具有更差的灵活便捷性，而导致未受伤事故概率增大(12.12%)，但其较好的行车稳定性却会减小轻伤和重伤事故的发生概率(7.66%和4.45%)，因此，建议提升两轮车的行车稳定性，增大三轮车的机动灵活性，并在车辆设计与制造环节进行差异化的限速管控。

4 结论

本文在剖析电动自行车-机动车事故时空分布等特性基础上，从6个方面确立该类事故严重性潜在影响因素集，应用4 类模型进行对比分析，选取拟合效果最优模型分析事故严重性影响因素，基于模型结果为道路交通管理部门提出事故防控措施，从而减轻电动自行车-机动车交通事故的不利影响。主要结论如下：

(1)以2018年绍兴市上虞区交通局电警系统中记录的10304 起电动自行车与机动车事故为数据基础，深入剖析该类事故的严重程度分布、时间及空间分布特性。

(2)从时间、空间、道路、环境、骑行者及车型等层面选择17 个事故严重性影响因素，采用MNL、OL、GOL及PPO模型进行拟合效果对比分析，基于AIC、BIC准则得出PPO模型为拟合度最佳模型。

(3)以拟合效果最优的PPO 模型及其13 个显著影响因素的边际效应，对该类事故严重性影响因素进行定量分析，总结出不同因素的影响显著性与差异性及是否违背平行线假设，并为道路交通管理部门提出针对性改善建议。