公交驾驶员违规类型同交通事故间的关联分析

朱彤，秦丹，董傲然，杜雨萌，魏雯

(长安大学，运输工程学院，西安 710064)

0 引言

公交车作为现代城市交通的重要组成部分，保障公交运行安全对于城市客运系统高效运转具有重要作用。公交车普遍被认为比其他机动交通方式更安全，然而由于城市道路交通环境复杂，公共交通事故的发生也难以避免，2019年全国累计发生1421起涉及公共汽车的道路交通事故，并造成327人死亡[1]。虽然道路上公交车比其他类型的机动车少，但由于公交车乘客容量较大，公交车事故会造成更严重的财产损失和人员伤亡，有必要进一步探究公交车事故致因机理。

目前，国内外对于公交车事故的研究多集中在驾驶员及乘客的受伤严重程度以及驾驶员的事故风险等领域。Chimba等[2]利用多项式Logit模型评估了影响公共汽车碰撞事故的显著因素，结果表明，车道宽度、车道数和车辆数等因素会影响受伤严重程度。围绕公交车事故率，Gu等[3]提出了一个时空随机效应零膨胀负二项模型来研究影响公交线路层面上的公交事故发生关键因素，结果表明，公交运营因素以及规划因素对公交车事故发生具有显著影响。Af Wåhlberg等[4]发现，离职的公交车驾驶员事故数比在职的驾驶员多40%。

此外，学者也对驾驶员违规行为的影响进行了研究。朱春莹等[5]通过调查问卷的方式探究了其职业压力的影响因素，结果表明，公交车驾驶员职业压力程度较高，有违规记录的驾驶员职业压力显著高于无违规记录的驾驶员。高红丽等[6]利用调查问卷发现，知觉行为控制、行为态度和过去防御性驾驶行为对防御性驾驶行为意向具有一定正向影响。此外，Mallia等[7]研究发现，自我报告的违规行为与公交车驾驶员的事故风险有关。日常驾驶行为可以作为风险驾驶员的指示信号，特别是违规行为可以反应驾驶员的意图和情绪[8]，这也是导致事故的主要人为因素。以往研究验证了事故风险与违规行为倾向之间的正相关关系[9]。然而，不同的违规行为可能会对碰撞风险产生不同的影响，却少有研究考虑到违规行为类别间的差异。

驾驶行为研究的数据采集方法包括驾驶员行为问卷、视频采集、相关运营公司记录等手段。以往的研究大多是通过问卷进行的，虽然该方法广泛应用于交通安全研究，但由于问卷中的偏差，驾驶员的自我报告数据可能存在误报、漏报的可能，从而导致有偏差的估计结果。考虑公交车驾驶员事故数据中零观测值过多的情形，采用零膨胀模型更为合适。此外，相比于传统计数模型，随机参数模型拟合效果更优，且捕捉了可能的随机变量，但它并未解释造成随机系数的可能影响因素，为此发展了考虑均值和方差异质性的随机参数模型方法。

本文通过构建具有均值和方差异质性的随机参数零膨胀泊松模型，利用公交运营公司的真实事故及违规数据，以公交车驾驶员发生的事故次数为研究对象，结合边际效应，定量分析驾驶员的违规行为次数对其事故率的影响，以期为高危险驾驶员的确定提供理论依据，并提高安全推断的可靠性。

1 数据描述

本文使用的公交车驾驶员事故及违规数据来自于国内某市公交公司营运安全管理系统，数据包括2019—2020年4532 项有记录且未重复的违规及事故数据，其中违规4035 项，事故497项，涉及42 条线路上的1356 名驾驶员。在这两年内，1356 名公交车驾驶员中有1000 名驾驶员(占比73.75%)发生过违规行为而未发生事故，零事故的占比较大，具有零膨胀数据的特点。其余356名驾驶员(占比26.25%)均发生过次数不等的事故。因变量为每一个公交车驾驶员在2019—2020年间的事故起数，自变量为驾驶员这两年间各类违规行为的违规次数和驾驶员属性，表1和表2分别给出了连续变量和分类变量的描述性统计结果。图1为公交车驾驶员事故频次的直方图。

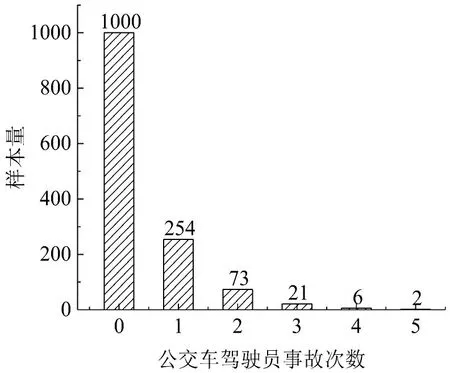
图1 公交车驾驶员事故频次分布Fig.1 Frequency distribution of bus driver's crashes

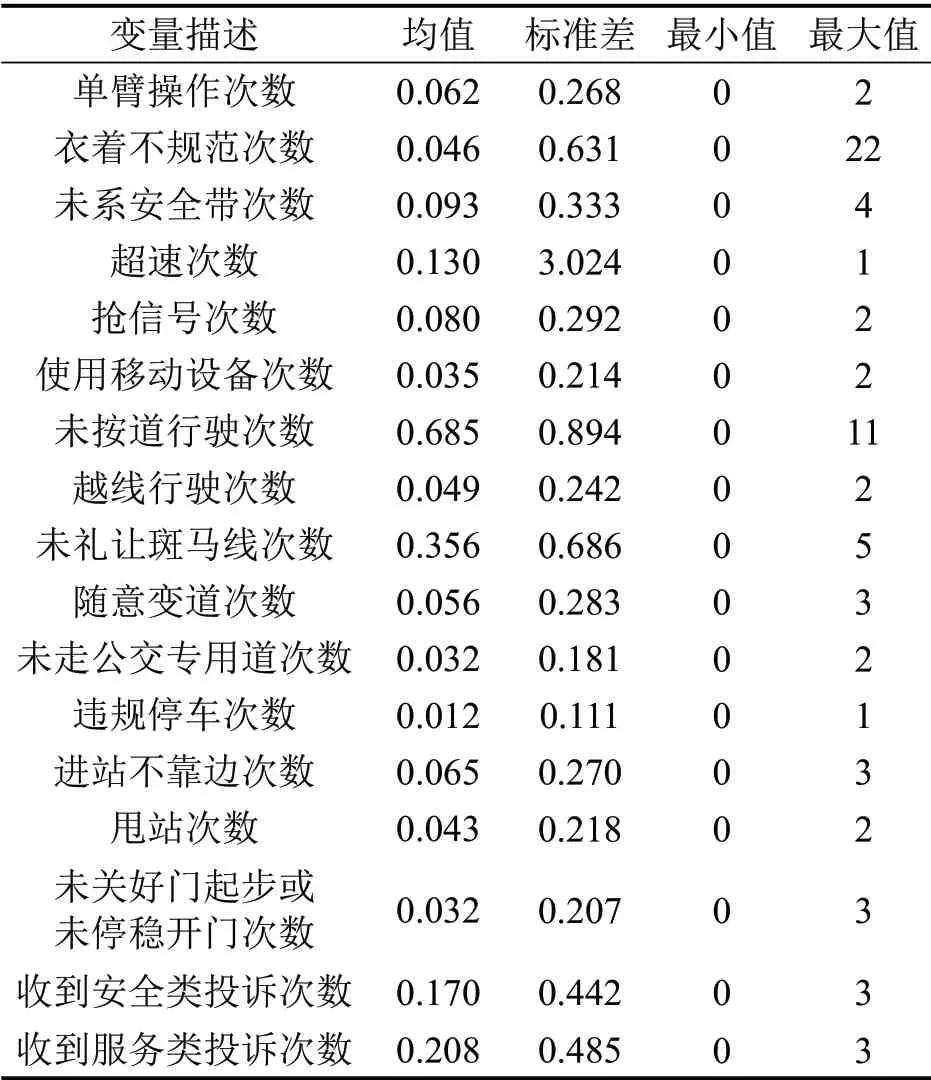
表1 连续变量描述性统计Table 1 Description of continuous variables

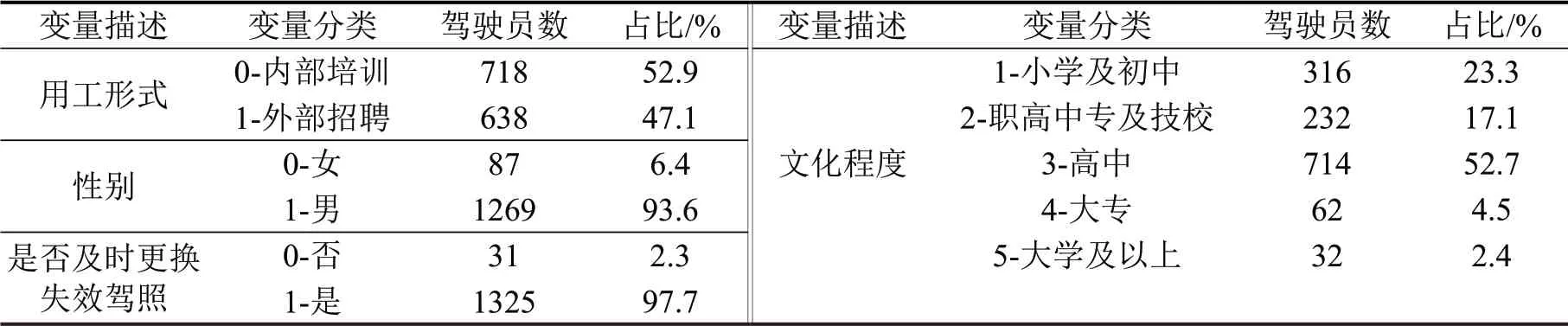
表2 分类变量描述性统计Table 2 Description of categorical variables

2 模型构建

2.1 建模框架

泊松模型(Poisson)适用于广泛的计数数据，表达式为

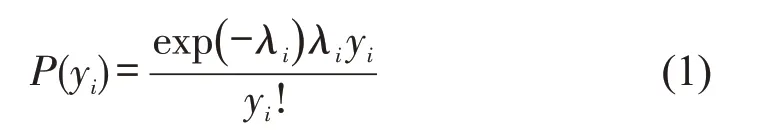
式中：P(yi)为发生yi起事故的频率；λi为驾驶员i的泊松参数，也是驾驶员i的预期事故数。Poisson模型具有限制性的等分散性，要求期望和方差均等于泊松参数。

在某些现象中，在观测周期内对零事件的观测可以由两种性质不同的条件产生。存在两种状态，一种是正常计数过程状态，另一种是零计数状态。考虑这种双态系统的模型被称为零膨胀模型，零膨胀泊松(zero-inflated Poisson,ZIP)模型由一个离散零分布和泊松分布组成，即

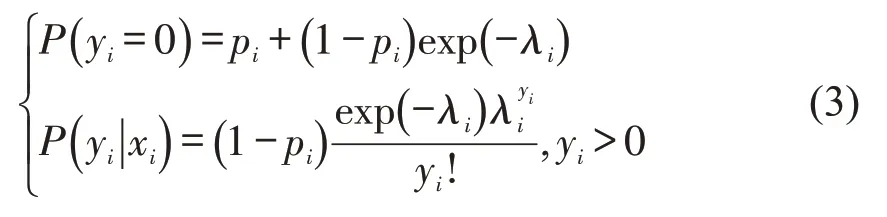
式中：pi为处于零状态的概率。最大似然估计法用于估计ZIP模型的参数，置信区间通过似然比检验来构造。

通过允许自变量的参数随观测值的变化而变化，随机参数模型可以很好地解释数据中未观测到的异质性，因此对ZIP 模型中引入随机参数，即随机参数零膨胀泊松模型(RPZIP)为

式中：βi为观测值i的参数；β为所有观测值的平均参数估计值；Δi服从均值和方差分别为0 和σ2的正态分布，是一个随机分布的误差项，可以捕捉未观察到的异质性。因此βi变成了可以随观测值变化而变化的可估计参数。如果一个参数的估计标准偏差明显不同于零，则视该参数为随机参数；否则，视该参数为固定参数。

过去几乎所有涉及随机参数模型的研究都假设随机参数的分布是独立的，即不同来源的未观察到的异质性之间没有相关性，这个假设可能是限制性的。本文引入一种更灵活的方法，允许每个潜在随机参数的均值和方差作为解释变量的函数，以捕捉观察因素之间相互作用产生的未观察到的异质性。βi是捕捉随机参数均值和方差异质性的关键参数，即

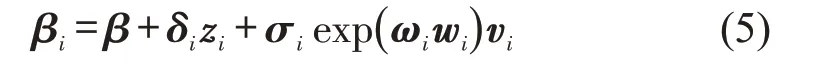
式中：zi为捕捉βi中均值异质性的解释变量向量；δi为相应的可估计参数向量；wi为属性向量，用于捕捉具有相应参数向量ωi的标准差σi的异质性；vi为干扰项向量。结构如式(5)所示，它允许两个不同的属性向量(zi和wi)影响不同观测值的参数值。

2.2 模型检验

2.2.1 过度离散检验

过度离散检验(Overdispersion tests)的假设为

式中：H0为零假设；H1为备择假设；μi为Poisson模型的期望值；α为散度系数；g(μi)为离散检验值。在等离差的零假设下，统计量具有一个自由度的极限卡方分布值3.84，当过度离散检验的值g(μi)大于临界值3.84时，拒绝零假设，继续寻找限制更少的模型；反之则接受零假设，认为数据不具有过度离散，适用于Poisson模型。

2.2.2 Vuong检验

通常采用Vuong 检验来选择最优模型，Vuong检验的假设为

式中：和Sm为mi的均值和标准差；N为总例数。V近似服从标准正态分布，若V≥1.96，模型1优于模型2；若V≤-1.96，模型2 优于模型1；若|V|＜1.96，则不能表明模型的优劣。

2.2.3 拟合优度检验

总体统计性能可以由收敛时的对数似然函数值LL(β)、Akaike 信息准则(EAIC)和McFadden Pseudo R-Squared (ρ2)指标来评估，计算方法分别为

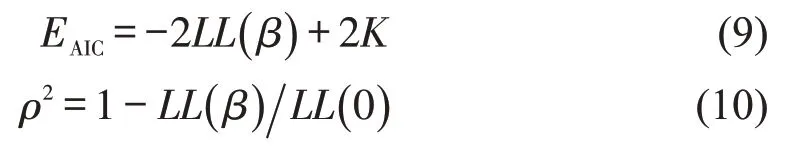
式中：LL(0)为仅含常数项的对数似然函数值；K为自由参数个数；指标LL(β)和EAIC值越小，ρ2越大，模型的拟合效果越好。

2.2.4 边际效应分析

通过边际效应来解释自变量对因变量的影响，本文因变量是公交车驾驶员事故频率。边际效应反映独立变量“一个单位”的变化对事故频率的影响，变量xi的边际效应可以用计算。

3 公交车驾驶员事故频率分析

表3为公交车驾驶员的Poisson 模型和RPZIP模型的估计结果，显著性水平为0.1，保留显著性水平低于0.1 的变量，并给出了RPZIP 模型的边际效应。表3中的过度离散检验值为3.280，低于3.84，在此基础上接受零假设，即无需继续寻找限制较少的模型，表示数据适用于泊松模型[10]。表3中的Vuong检验值为6.864，表明零膨胀模型优于非零膨胀模型。如表3所示，RPZIP 模型的LL(β) 值为-912.950，AIC 值为2026.1，均小于Poisson 模型，RPZIP 模型的McFaddenρ2=0.146 大于Poisson 模型，这些结果表明，RPZIP 模型在统计上优于Poisson 模型。本文将对RPZIP 模型的结果进行解释。RPZIP模型分为计数态和零态，计数态的显著因素对公交车驾驶员事故频率有显著影响，零态的显著变量影响驾驶员零事故的发生。计数态有3个随机参数，分别为未系安全带次数、未礼让斑马线次数和及时更换失效驾照；零态有1 个随机参数，为及时更换失效驾照。

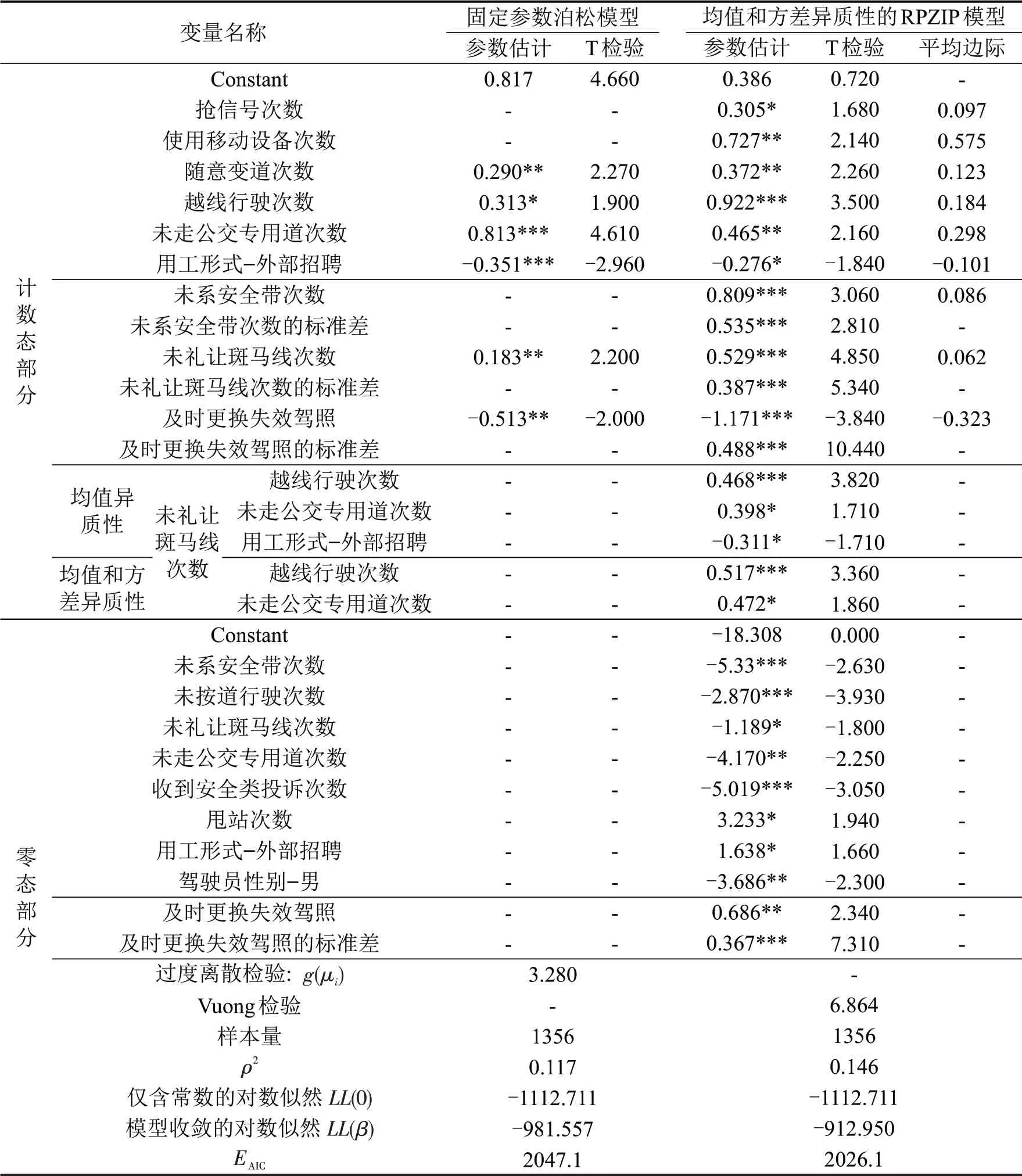
表3 泊松回归模型及随机参数零膨胀泊松模型参数估计结果Table 3 Model estimation results of Poisson and random parameters zero-inflated Poisson model

3.1 随机参数分析

未系安全带次数对公交车驾驶员事故频率有着显著影响，其参数服从均值为0.809，标准差为0.535的正态分布，该分布概率密度如图2所示。这表明随着未系安全带的次数增加，大部分驾驶员会发生更多的事故，但其影响效应存在波动性。安全带是有效的驾驶保护设施，安全带在车辆翻滚或碰撞过程中对乘员具有有效的保护作用，经常不系安全带的驾驶员具有较差的风险意识。因此，可考虑进一步管理措施与技术手段保障安全带佩戴，对于未按规定佩戴安全带的驾驶员予以进一步跟踪调查。

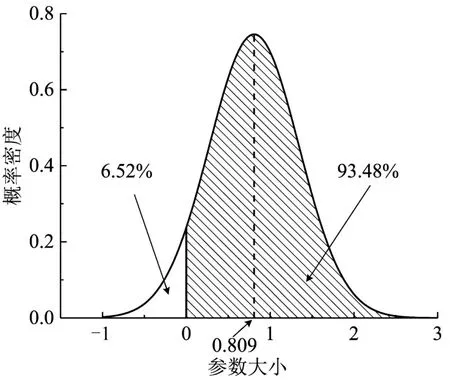
图2 “未系安全带次数”参数分布Fig.2 "Times of not wearing seat belt"parameter distribution

未礼让斑马线次数显著影响着公交车驾驶员的事故频率。未礼让斑马线次数的参数服从均值为0.529，标准差为0.387 的正态分布，其概率密度图如图3所示。表明未礼让斑马线的次数多，对大部分驾驶员来说意味着有较高的事故率，但在不同的驾驶员之间，其影响效应存在差异；平均而言，随着未礼让斑马线次数增加一个单位，公交车驾驶员事故数增加6.2%。此外，未礼让斑马线这一随机参数变量在越线行驶次数、未走公交专用道次数和外部招聘这3 个变量中具有均值和方差异质性。未礼让斑马线次数的均值异质性与外部招聘呈负相关，外部招聘使得未礼让斑马线次数参数均值变为0.218(0.529与0.311之差)，概率密度图的变化如图4所示。表明相比与内部培训的员工，用工形式为外部招聘的驾驶员会降低事故频率。

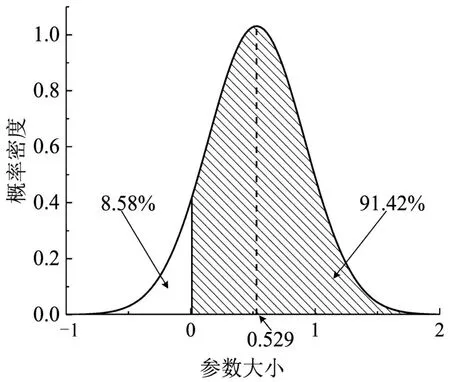
图3 “未礼让斑马线次数”参数分布Fig.3 "Times of not yielding to pedestrians"parameter distribution

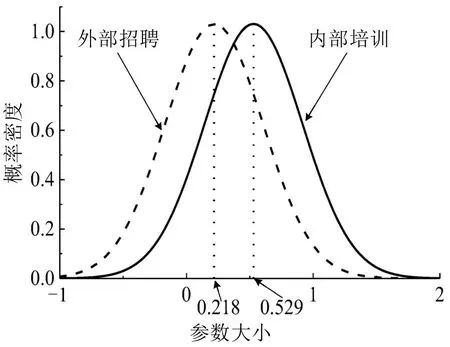
图4 “未礼让斑马线次数”在“用工形式”下的参数分布(均值异质性)Fig.4 Distribution of"times of not yielding to pedestrians"under"employment form"(Mean heterogeneity)

越线行驶次数参数估计系数均为正，使得未礼让斑马线次数参数均值变为0.997(0.529与0.468之和)，概率密度图的变化如图5(a)所示。此外，发现未礼让斑马线次数产生了均值和方差的异质性随机参数，越线行驶次数不仅增加了未礼让斑马线次数的均值，还使得未礼让斑马线次数参数的方差增加至0.667，即0.3872+0.517=0.667，概率密度图的变化如图5(b)所示。未走公交专用道次数参数估计系数也为正，使得未礼让斑马线次数参数均值变为0.927，即0.529 与0.398 之和，概率密度图的变化如图6(a)所示。同样地，未走公交专用道次数不仅增加了未礼让斑马线次数的均值，还使得未礼让斑马线次数参数的方差增加至0.622，即0.3872+0.472=0.622，概率密度图的变化如图6(b)所示。

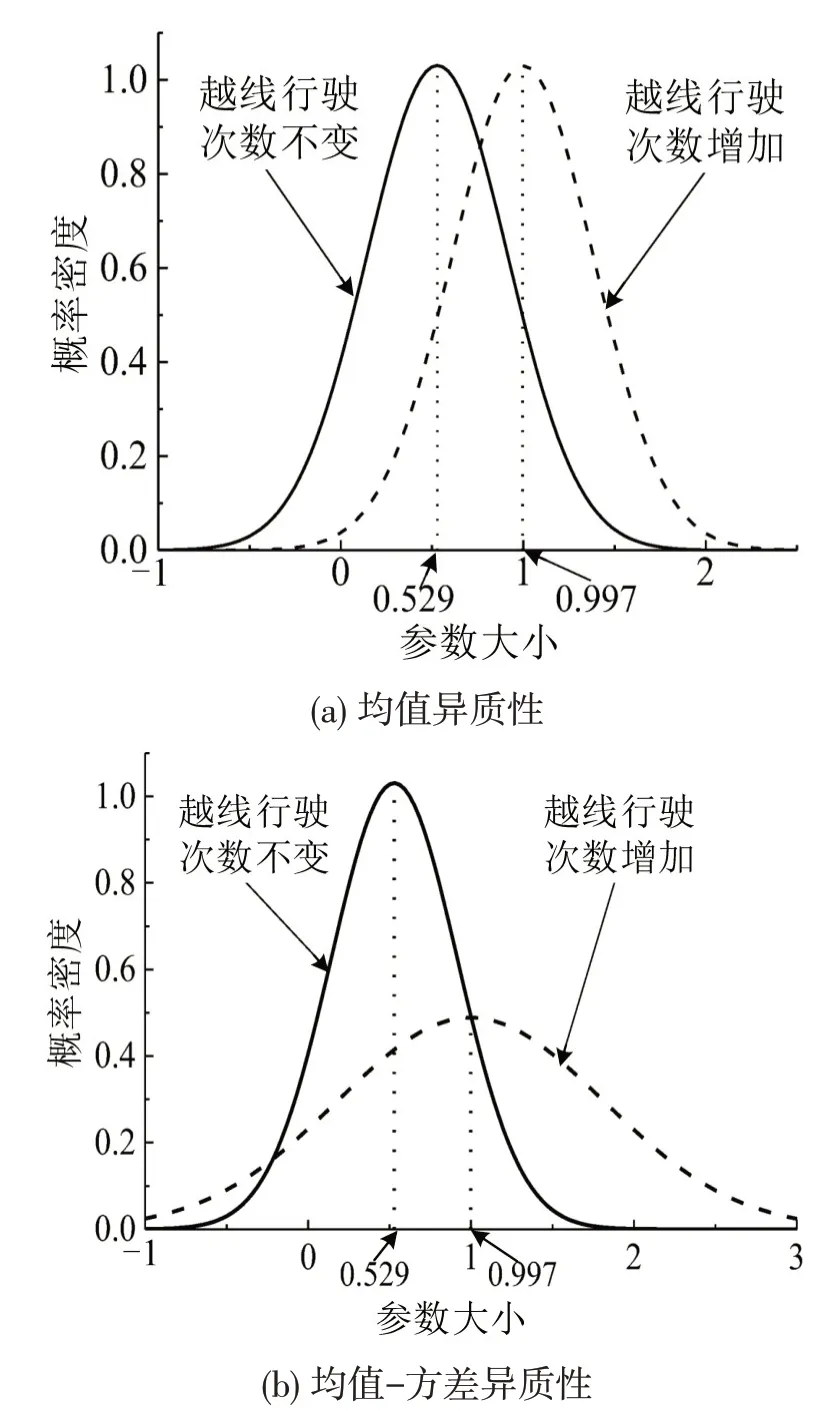
图5 “未礼让斑马线次数”在“越线行驶次数”下的参数分布Fig.5 Distribution of"times of not yielding to pedestrians"under"times of pressing the line"

图6 “未礼让斑马线次数”在“未走公交专用道次数”下的参数分布Fig.6 Distribution of"times of not yielding to pedestrians"under"times of not driving on bus lane"

上述结果表明，随着未礼让斑马线次数的增加，驾驶员的事故频率也会增加，而驾驶员越线行驶次数和未走公交专用道次数的增加会进一步导致这种不良的安全影响显著增加。越线行驶次数和未走公交专用道次数越高，未礼让斑马线次数参数的方差就越高。这些发现强调了公交车驾驶员事故频率数据中该变量的复杂性。不仅需要重点关注经常未礼让斑马线的驾驶员并对其采取相应的管理处罚措施，对于经常发生越线行驶和未走公交专用道驾驶行为的驾驶员，也需要关注和考核，可以采取减少其驾驶工作时长、配以辅助驾驶员等措施来减少事故的发生。此外，相应公交运营单位可适当选择对外招聘的驾驶员以降低事故率。

计数态研究结果表明，及时更换失效驾照的参数服从均值为-1.171，标准差为0.488的正态分布，其概率密度图如图7(a)所示。这意味着对绝大多数公交车驾驶员(99.18%)而言，及时更换失效驾照会显著降低其事故数，而对于极少数驾驶员(0.82%)而言，则会增加；相较于驾照失效后不及时更换的驾驶员，及时更换有效证件的驾驶员发生事故数减少了32.3%；在零态部分，及时更换失效驾照的参数服从均值为0.686，标准差为0.367的正态分布，其概率密度图如图7(b)所示。这意味着对3.08%的公交车驾驶员而言，及时更换失效驾照会减少“零事故”的发生，即会增加事故发生概率；对于另外96.92%的驾驶员，及时更换失效驾照会降低事故发生的概率。结果表明，能及时更换失效驾照的驾驶员具有更加谨慎的驾驶态度。

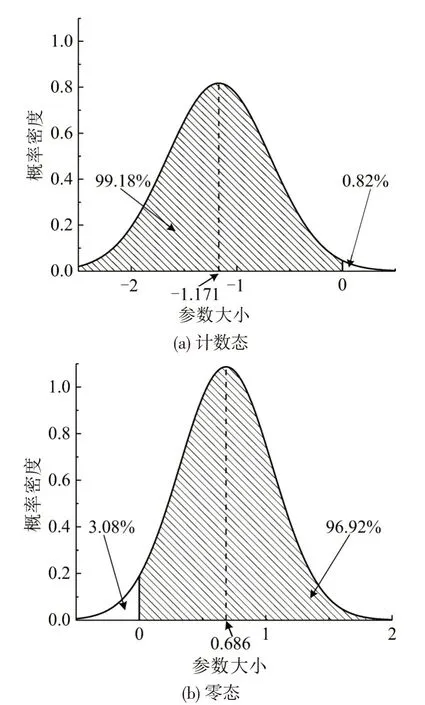
图7 “及时更换失效驾照”参数分布Fig.7 "Updating license in time"parameter distribution

3.2 非随机参数分析

使用移动设备次数行为的边际效应值为57.5%，对于驾驶员事故频率的增加影响最大，未走公交专用道次数在计数态部分的系数为正值，该违规行为次数每增加一个单位，驾驶员的事故频率增加29.8%。未走公交专用道次数与零事故的发生显著负相关，即随着未走公交专用道次数的增加，零事故发生的可能性越低，则驾驶员发生事故的概率越大。这与任高晓等[11]的研究结果一致，在交通信号临近转换时抢行通过、使用移动设备和随意换道等驾驶行为属于冒险驾驶风格，驾驶员在驾驶中的事故频率与冒险驾驶风格次数呈正相关。

零态部分的未系安全带次数、未按道行驶次数、未礼让斑马线次数和收到安全类投诉次数5个变量的参数估计结果为负值，即随着这些违规行为次数的增加，驾驶员的事故率不太可能具有零值，预期事故发生的概率会增加。甩站次数对于驾驶员是否发生事故有着显著影响，甩站次数的系数为正值，表明会增大发生零事故的可能性，则驾驶员发生事故的可能性降低。

计数态部分的驾驶员用工形式对于其事故频率有着显著影响。用工形式为外部招聘的驾驶员发生事故的频率显著低于用工形式为内部培训的驾驶员，外部招聘的公交车驾驶员会使事故频率降低10.1%。此外零态部分的驾驶员用工形式也显著影响零事故的发生，相比于内部培训的员工，表明其会增加零事件的发生。这可能是由于外部驾驶员驾驶经验丰富，而内部培训的驾驶员上岗门槛较低。与女性驾驶员相比，男性驾驶员会显著降低零事故的发生，即会增大发生事故的概率，这与前人的研究结果一致，原因是男性驾驶员的驾驶行为更加冒进，进而导致增加发生事故的概率。

4 结论

本文基于均值和方差异质性的随机参数零膨胀泊松模型，探究了城市公交车驾驶员违规行为次数与事故频率之间的关联机理，得到以下结论：

(1)驾驶员违规行为与事故频率具有明显的关联性。使用移动设备次数等违规行为与高事故频率有关，并具有较大的边际影响。相反，其他类型的违规行为与事故频率并未发现显著的相关关系。这进一步说明在研究中对违规类别予以区分的必要性。

(2)未礼让斑马线次数的增加，对于大部分驾驶员来说意味着更高的事故率，但在驾驶员个体之间其影响效应存在类正态性波动。未礼让斑马线次数与越线行驶次数及未走公交专用道次数显著相关，它们会进一步导致事故频率显著增加。

(3)未走公交专用道次数与越线行驶次数会显著影响事故频率，但在生活中这两类违规行为很容易被忽视。因此，建议在公交车上安装能够提醒驾驶员超越专用道或越线的车载智能设备。此外，经常不系安全带和未能及时更换失效驾照的驾驶员应是接受重点监督的关键群体。

(4)外部招聘驾驶员和内部培训驾驶员与事故频率之间的关系具有明显差异，内部培训驾驶员具有更高的事故率。因此有必要深化健全内部培训机制，加强驾驶员的上岗监督。

本文为公交车驾驶员事故频率研究提供了新的见解与探索方向，但仍存在不足之处。主要的局限在于本文未展开对于心理特征的调查研究。驾驶员表现出违规行为，可能是由于其具有抑郁、焦虑等心理特征。未来的研究可通过构建个人心理特征变量并建立其与事故率之间的关系，进一步探究引发事故的心理因素。