借助启发性提问 提高数学教学效益

安徽省合肥一六八中学 史传奇 （邮编：230601）

高中数学知识点多习题情境复杂多变，教学中如不注重相关方法的变式应用，很容易使学生产生枯燥感，挫伤学生学习的积极性.其中启发性提问能够指引学生向着正确的方向思考问题，营造宽松活泼课堂氛围的同时，有效地避免学生走进理解的误区，促进学生解题效率与解题能力的提升，因此高中数学教学实践中应注重启发性提问的运用，给高中数学课堂增添光彩.

1 借助启发性提问，提高函数奇偶性应用的灵活性

奇偶性是函数的重要性质，是各类测试的热门考点.教学中既要注重运用多媒体技术为学生展示奇函数与偶函数的图象特征，又要注重预留一定的时间要求学生认真观察图象，总结奇、偶函数图象的特点，启发其应用数学符号概括奇、偶函数的特性，如此既能加深学生印象，又能使其更好地理解“f(x)=f(-x)”“f(x)=-f(-x)”的含义，而非简单机械记忆.同时，为提高学生运用函数奇偶性解题的灵活性，课堂上应注重筛选、讲解经典例题，尤其为帮助学生更好地打开解题思路，应注重设计相关的启发性问题，使学生通过思考启发性问题，更好地找到解题的思路，增强其解题的自信心.如课堂上可向学生展示如下例题：

例1已知定义在R 上的偶函数f(x)，且当x≥0 时，f(x)=2x，若对任意x∈[0,2t+1]均有f(x+t)≥[f(x)]3，则实数t的最大值为（）

本题考查了函数的奇偶性、单调性、不等式、恒成立等知识，具有较强的综合性.要想顺利地解答该题，需要学生运用函数的奇偶性、单调性，脱去函数的“对应法则f”.教学中为使学生少走弯路，可提出一些启发性问题，采用一问一答的形式开展教学活动.

师：根据题意能否先粗略地求出t的取值范围？

生：由给定的区间“[0,2t+1] ”可得关系式2t+1 ＞0，可求得t＞-

师：能否直接将f(x)=2x代入到关系式“f(x+t)≥[f(x)]3”中？

生：要研究的函数是在给定的参数范围内，因此，可以直接代入.

师：代入后可得2x+t≥23x，即，x+t≥3x，这一关系式是否正确，为什么？

生：因给定的函数f(x)是偶函数，因此，代入后应转化为|x+t|≥|3x|，而非x+t≥3x.

师：接下来该怎么处理？

生：两边平方、整理，将问题转化为求8x2-2xt-t2≤0 在[0,2t+1] 上恒成立时t的取值范围，令g(x)=8x2-2xt-t2，由二次函数性质只需满足g(0)≤0,g(2t+1)≤0，解得≤t≤因此t的最大值为-故选A.

围绕例题巧妙地设计启发性问题，层层递进，引导学生不断地进行思考，不仅深化了学生对函数奇偶性的认识与理解，而且使其顺利地解出了正确答案，很好地调动了其学习的积极性，达成了预设的教学目标.

2 借助启发性提问，更好地掌握数形结合的应用思路

提高学生的解题能力是高中数学教学中的重要目标之一.为更好地实现这一目标，不仅需要认真细致地讲解高中数学基础知识，而且需要传授相关的解题思想、方法等，使学生在解题中能够透过现象看本质，迅速地找到解题的切入点.其中数形结合思想在解题中有着广泛的应用，教学中应注重围绕具体教学内容，启发性地提问学生，使学生掌握应用数形结合方法解题的具体思路，使其感受到解题的成就感.高中函数知识教学中应注重从学生熟悉的函数图象切入，引导学生根据自己的理解画出相关函数的图象.如由y=f(x) 的图象画出y=f(|x|)、y=-f(|x|)的图象，为数形结合方法的应用做好铺垫.另外，为使学生真正地体会数形结合方法的应用，可围绕以下习题开展教学活动：

例2已知函数f(x)=若关于x的方程f(x)=a(x+3)恰好有4 个不相等的实根，则a的取值范围为（）

本题考查了分段函数、方程、函数图象、导数、切线等知识点，较为综合，能很好地检测学生对基础知识的掌握情况.其中正确地画出函数的图象，深挖图象中的隐含条件是破题的关键所在.为使学生认识到这一点，应有启发性地对学生进行提问.

师：根据题意，方程有4 个不相等的实根，意味着方程两边的函数图象有什么关系？

生：方程两边的函数图象应有4 个不同的交点.

师：如何画出函数y=|x3-4x-1 |的图象？函数y=a(x+3)的图象恒过哪一个点？请尝试着在同一坐标系中画出这两个函数的图象.

生：先借助导数研究函数y=x3-4x-1 的单调区间和极值点，再画出它的图象，而后将处于x轴下方的图象关于x轴向上翻折，即可得到函数y=|x3-4x-1 |的图象.函数y=a(x+3)的图象恒过点(-3,0).两个函数的图象如图1 所示：

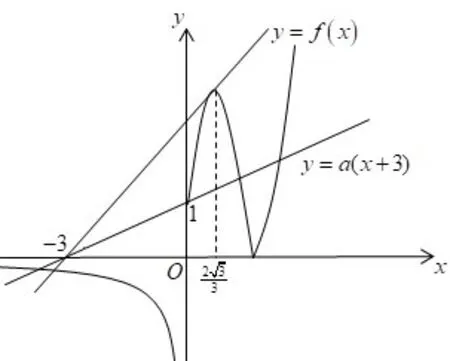
图1

师：若要满足题意，当x＞0 时，函数y=|x3-4x-1 |的图象和函数y=a(x+3)的图象应有几个交点？观察图象，如何求解符合上述交点的a的取值范围？

生：显然因为x＜0 时两个函数的图象必有1个交点，因此，当x＞0 时，函数y=|x3-4x-1|和y=a(x+3)的图象应有3 个交点，如图所示，函数y=a(x+3)的图象在两个临界位置之间的部分即满足题意.这里需要求出两个边界，当它过点(0,1)时，可得a=当它和曲线y=|x3-4x-1 |相切时的位置即为上边界.师：如何求上边界对应的a的值呢？

生：根据导数知识，通过设出切点，求出a的值.设切点坐标为(x0,-+4x0+1)，过切点的切线斜率为-3x02+4，对应的切线为y＝-4x0-1=(-+4)(x-x0)，将点(-3,0) 代入解得a=1，因此，a的取值范围为，故选D.

通过设计启发性问题促进学生思考，使学生深刻地体会到运用数形结合方法解决数学问题的便利之处，有效地提升了其运用数形结合解题的意识.同时鼓励学生进行系统的总结，很好地掌握了运用数形结合方法的解题思路，如解决复合方程根的问题，函数零点问题时，运用数形结合方法可有效地破题.

3 借助启发性提问，更好地掌握构造函数的技巧

解答高中数学习题的方法多种多样，尤其在解答函数习题中时常需要根据已知条件构造新的函数.而构造新的函数对学生分析以及理解问题的能力要求较高.教学中为提高学生构造函数的自信心，掌握构造函数的相关技巧，应注重从学生所学的基础知识入手，通过给予学生引导与启发，先要求其构造简单的函数，加深其对构造函数作用的认识.并根据学生的学习实际以及近年来高考中有关构造函数考查的规律与方向，为学生展示相关的习题，要求其通过构造函数加以解答，以更好的拓展其视野与能力，吃透构造函数的本质，在以后的解题中能够以不变应万变.如在讲解对数函数知识时，为学生展示如下习题：

例3已 知a、b∈(0,3)，且4 lna=aln 4,4 lnb=bln 2,c=log0.30.06，则（）

A.c＜b＜aB.a＜c＜b

C.b＜a＜cD.b＜c＜a

本题给出的条件较为简单，但是较为抽象，要想顺利地解答，需要对已知条件进行适当的变形，而后观察等式的结构特征，构造出合理的函数，借助函数的性质比较相关参数的大小关系.教学中为使学生少走弯路，尽快地找到突破口，应注重对学生进行启发性的提问.

师：由“4 lna=aln 4”能否求出a的值？

生：因为4 lna=aln 4，即4 lna=2aln 2，可以求得a=2.

师：如何将“4 lnb=bln 2”改写成分式的形式？

师：怎样比较c和2 的关系？

生：c=log0.30.06=log0.3(0.2×0.3)=log0.30.2+1＞log0.30.3+1=2，所 以c＞2，即c＞a，综 上分析可知b＜a＜c，故选C.

本题难度较大，对于大多数学生而言一时难以找到解题的思路.而通过启发性地提问学生，逐步启发引导，最终拨云见日，使学生顺利地找到了解题思路，很好地锻炼了学生构造函数解题的能力，积累了运用构造函数解题的相关技巧.

4 借助启发性提问，更好地把握运用函数周期性解题的细节

高中数学有关函数周期性的考查，常要求学生求解一些较大自变量的函数值.教学中为使学生更好地把握运用解题的相关细节，一方面，注重加深学生对函数周期性的认识与理解，尤其结合高中数学中一些具体的周期函数，与学生一起总结周期函数的相关性质以及推导函数周期性的相关思路，使学生能够熟练地掌握.另一方面，注重组织学生开展针对性的训练活动，给学生带来良好的解题启发，使其认识到运用函数周期解题时常需要与函数的奇偶性、单调性结合起来.同时，注重对学生进行启发性的提问，通过驱使学生进行有深度的思考，使其尽快地推导出函数的周期，以顺利地解答习题.教学中可组织学生围绕以下习题开展专题训练活动：

例4已知函数f(x)=1，若定义在R 上的奇函数g(x)，满足g(1-x)=g(1+x)，且g(1)=f(log225)+f则g(2019)的值为（ ）

A.2 B.0 C.-1 D.-2

本题给出的函数表达式较为复杂，而且较为抽象，很多学生审题后不知所措.课堂上应引导学生树立必胜的信念，通过给予学生启发性的提问，逐步引导学生化难为易，运用所学的函数周期加以巧妙地突破.

师：由函数f(x)，探讨f(x)+1 的奇偶性是怎样的？

生：由对数运算法则可知f(log225)+=f(2 log25)+f(-2 log25)，g(1)=f(2 log25)+f(-2 log25).

师：怎样建立g(1)和h(x)之间的关系？

生：g(1)=f(2 log25)+f(-2 log25)=h(2 log25)-1+h(-2 log25)-1=-2，因为g(x)为奇函数，则g(-1)=-g(1)=2.

师：g(2023)中自变量的数值很大，要求其值需要运用到周期，那么怎样结合上面问题的结论以及“g(1-x)=g(1+x)”推出g(x)的周期呢？

生：因为g(1-x)=g(1+x)，可知g(x)的图象关于直线x=1 对称，则g(4+x)=g[1+(x+3)]=g[1-(x+3)]=g(-x-2)=-g(x+2)=g[1-(x+1)]=-g(-x)=g(x)，所以g(x)的周期为4，则g(2023)=g(4×506-1)=g(-1)=2，故选A.

课堂上对学生进行启发性提问，实际上在帮助学生梳理解题思路，学生经过积极的思考与回答教师提出的问题，成功地解答成了该题.

高中数学教学中应充分认识到启发性提问的重要价值，尤其是结合具体教学内容做好问题的设计.课堂通过启发性地提问学生，营造民主的课堂氛围，拉近与学生距离的同时，进一步深化学生对所学知识的理解，指引其迅速地找到解题的思路与方法，为其数学学习成绩的提升做好铺垫.