指向深度学习的教学设计与思考
——以高一函数的教学为例
北京理工大学附属中学 金永涛 (邮编:100089)
1 问题提出
数学教学“重结论轻过程”的现象由来已久,导致学生多以低阶的学习活动为主,缺少深度参与和深度思考.学生对数学知识及知识所蕴含的数学思想更多地停留在浅层次的认知水平,缺少深刻的领悟.数学教学是数学思维的教学,只有教师具有深度教研的意识、能力和素养,在日常教学中一贯坚持指向深度学习的教学设计与实践,才能确保深度学习的发生.罗增儒教授指出:数学家创造了数学知识,数学教师创造了对数学知识的理解.伴随着学生深度学习的持续发生,学生和教师都会取得更大的提升,更好地实现教学相长.
2 对数函数与二次函数的复合函数性质探究
2.1 教学现状与设想
在对数函数的教学中,经常遇到形如下面的问题:
已知函数f(x)=log2(-x2+2x+3),求函数的增区间和减区间,或求函数的最大值等问题.
学生通常是利用复合函数的单调性口诀“同增异减”进行解答,而对这类函数的性质了解甚少,这也是解题会出现重结论、套路化的重要原因.为了改变学生机械化和被动接受式的学习方式,强化学生的深度学习和高阶思维参与,设置学习专题:系统研究函数f(x)=ln(ax2+bx+c)(a≠0)的性质,应用性质解决实际问题.进而,利用函数性质,尝试画出函数图象——图象是对函数性质的直观呈现.
2.2 教学设计与实施
学习任务研究函数f(x)=ln(ax2+bx+c)(a≠0)的性质.
引导问题1怎么开展研究?以前有无类似的经历?
引导学生对要研究的函数进行分析、类比、联想和思考,确定出研究的策略:类比研究二次函数的过程与方法.在此基础上,再确定研究思路:采用从特殊到一般的研究方式,从特殊的、简单的函数入手,利用函数之间的内在联系逐步深入,系统掌握函数的性质.
引导问题2需要考虑哪些影响因素?
引导学生梳理在研究函数性质时,需要考虑a>0 与a<0,还要考虑△=b2-4ac的正负取值情况及函数的定义域.
引导问题3如何开展具体的研究?
活动一先研究函数f(x)=lnx2的性质.注意到定义域为{x|x≠0},零点为-1 和1,且f(x)是偶函数,可将函数进行变形f(x)=lnx2=2 ln |x|,这样一来,f(x)就与熟悉的函数y=lnx建立起联系,可作出函数f(x)的图象(图1).
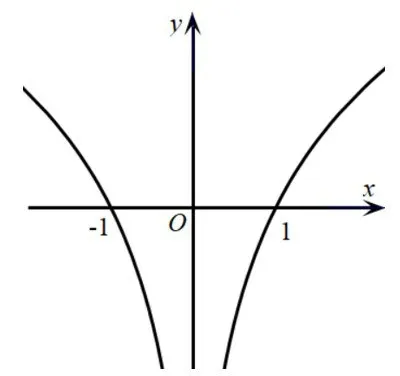
图1
活动二研究函数f(x)=lnax2(a>0 且a≠1)的性质.引导学生应用对数的运算性质,可得f(x)=lnx2+lna,注意到lna可以是任意非零的实数,f(x)可由y=lnx2通过向上或向下平移得到.由此可以猜想,当函数的真数部分是关于x的二次函数时,f(x)与y=lnx存在密切的联系,并非陌生的曲线.
引导问题4下面又该研究哪个函数呢?研究过程需要关注哪些因素?
活动三研究一般形式的函数f(x)=ln(ax2+bx+c)(a>0) 的性质.此时,函数仍然有对称轴且为x=-,要考虑定义域的变化,即ax2+bx+c>0.当△<0 时,ax2+bx+c>0 在实数集R 上恒成立,定义域为R.如f(x)=ln(x2+2x+2),变形可得f(x)=ln [(x+1)2+1],可知最小值f(-1)=0,f(x) 在(-∞,-1) 内递减且在(-1,+∞)内递增,根据函数的性质作出函数图象(图2);当△≥0 时,记方程ax2+bx+c=0 的两个实根为x1和x2且x1≤x2,则定义域为(-∞,x1)⋃(x2,+∞),如f(x)=ln(x2+2x-3),定义域为(-∞,-3)⋃(1,+∞),对称轴为x=-1 即f(x)=f(-2+x) 成 立,x=-3 和x=1 是两条渐近线,即
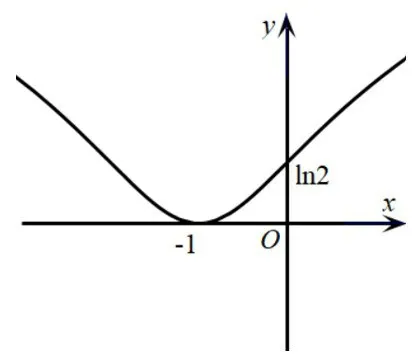
图2
x→1 ⇒x2+2x-3 →0 ⇒f(x)→-∞且
x→-3 ⇒x2+2x-3 →0 ⇒f(x)→-∞,f(x)在(-∞,-3)内递减且在(1,+∞)内递增,根据函数的性质作出图象(图3).观察可知,f(x)在(1,+∞)内的图象类似于我们熟悉的对数函数.
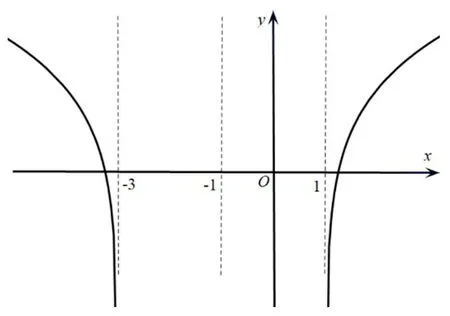
图3
引导问题5对于这一类型的函数,我们的研究全面吗?
活动四研究f(x)=ln(ax2+bx+c)(a<0)的性质,此时须满足ax2+bx+c>0 存在实数解,函数仍然存在轴对称且对称轴为x=-.如f(x)=ln(-x2+2x+3),定义域为(-1,3),对称轴为x=1,最大值f(1)=ln 4,x=-1 和x=3 是两条渐近线即x→-1 ⇒x2+2x-3 →0 ⇒f(x)→-∞且x→3 ⇒x2+2x-3 →0 ⇒f(x)→-∞,f(x)在(-1,1)内递增且在(1,3)内递减,根据函数的性质作出图象(图4).
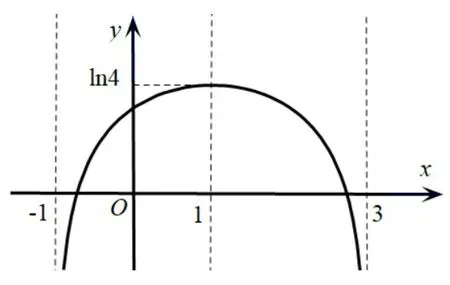
图4
2.3 评价与反馈
反馈练习已知f(x)=log2,解不等式f(a)<f(-a).
解析分析可得f(x)在定义域(-1,1)内单调递减,且为奇函数,再由f(0)=0,解得0 <a<1.
3 教学感悟
(1)深度教研是深度学习的根本前提
指向深度学习的教学设计,首先需要教师具备深度教学的意识、能力和素养,以学生的认知发展规律为基础,以实现知识理解的系统性和深刻性、探究和把握数学知识本质为根本,以揭示知识蕴含的数学思维、灵活运用数学思想方法创造性地分析和解决问题为核心,进行深度教学设计、深度学法指导设计和多元评价与反馈.
(2)学法指导是深度学习的根本保障
教师不仅要研究教学,还要研究学法,站在学生的视角审视数学的学习.引导学生有效开展观察与分析、数学运算与逻辑推理、交流与反思,提升学生的数学综合能力和素养.培养学生深度学习的意识,提升学习的效率和质量;培养学生的探究意识,努力揭示知识的本质和问题的本源;培养学生的多元思维,提升迁移能力、逆向思维和批判思维能力.
(3)深度学习是提升思维能力,落实核心素养的根本途径
波利亚说:“解题就像采蘑菇一样,当我们发现一个蘑菇时,它的周围可能有一个蘑菇圈.”深度学习,让学生学会用联系的观点、发展的观点看问题,用辩证的方式分析和思考问题,有助于提升学生的“四能”.依托深度学习,不断培养学生的高阶思维能力和思维品质,切实落实数学核心素养.

