函数图象中的“幽灵”

安徽省宁国中学 陈晓明 （邮编：242399）

在有关集合的运算中，我们常常说“空集”像一个幽灵：来去匆匆，在运算中经常忽略它的存在而付出代价！近来笔者发现渐近线更像是函数图象中的幽灵，同样我们会经常忽略它的存在而功亏一篑！

下面是笔者所在学校参加的各级各类考试中学生出错率相当高的一类试题，它们都与函数图象中的渐近线有关.

例1已知直线y=2a与函数y=|2x-2|的图象有两个公共点，则实数a的取值范围是____.

错解首先画出函数y=2x的图象（过定点(0,1)），然后向下平移2 个单位，得到函数y=2x-2 的图象（过定点(0,-1)），再把x轴下方的图象沿x轴翻折到x轴上方（翻折变换），从而得到函数y=|2x-2|的图象，如图1 所示.若直线y=2a与函数y=|2x-2 |的图象有两个公共点，则只需2a＞0，即实数a的取值范围是(0,+∞).

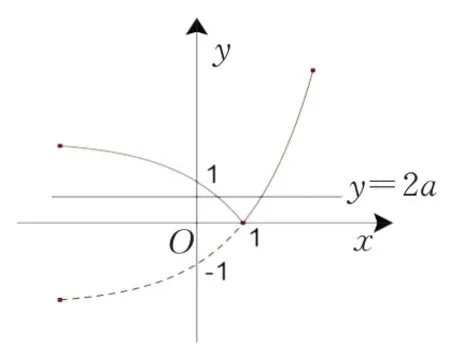
图1

剖析该解法错在忽略了函数图象的渐近线的存在.因为函数y=2x的图象的渐近线是x轴（y=0），图象向下平移2 个单位后渐近线是y=-2，如图2所示，把x轴下方的图象沿x轴翻折到x轴上方后渐近线是y=2，因此，若直线y=2a与函数y=|2x-2| 的图象有两个公共点，则0 ＜2a＜2，即实数a的取值范围是(0,1).

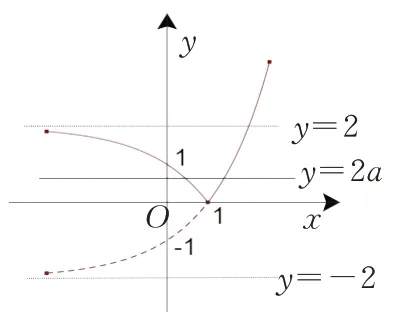
图2

变式（1）若直线y=2a与函数y=|2x-2 |的图象有一个公共点，则实数a的取值范围是__________.（答案：[1,+∞)⋃{ 0}）

（2）若直线y=2a与函数y=|2x-2 |的图象没有公共点，则实数a的取值范围是______.（答案：(-∞,0)）

（3）若直线y=2a与函数y=|ax-1（|a＞0 且a≠1）的图象有两个公共点，则实数a的取值范围是_________（答案

（4）若函数y=的图象与x轴有交点，则实数m的取值范围是_________.（答案：(0,1]）

例2已知函数f(x)=x(lnx-ax)有两个极值点，则实数a的取值范围是___________.

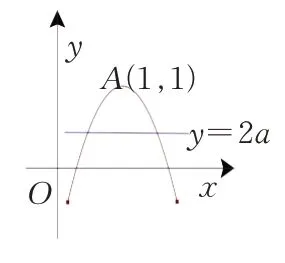
图3

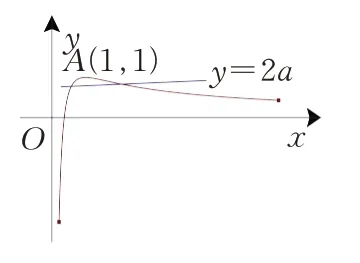
图4

例3函数f(x)=ax3-3x2+1，若存在唯一的零点x0，且x0＞0，则a的取值范围是（）.

A.(2,+∞) B.(1,+∞)

C.(-∞,-2) D.(-∞,-1)

错解（分离参数法）因为f(x)=ax3-3x2+1，所以x=0 不是函数的零点.

通过g(x)的大致图象可知，若函数h(x)=a（常数函数，图象是一条水平直线）与g(x)=的图象有唯一交点P(x0,y0)（且x0＞0）是不可能的，交点个数只可能是2或3 或4.因此该试题有误.

剖析问题出在函数g(x) 的大致图象上：如图6所示，当x＞1 时，g(x)=＞0，故图象应 在x轴上方；当x＜-1 时，g(x)=＜0，故图象应在x轴下方.因此出错的原因仍然是忽略了该函数图象的一条渐近线：x轴.由图6可知a的取值范围是(-∞,-2)，故本题正确答案是C.

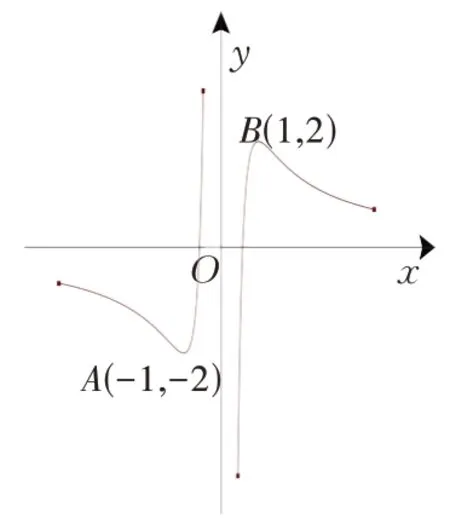
图6

变式1若函数f(x)=ax3-3x2+1 有唯一零点，求a的取值范围.（答案：(2,+∞)⋃(-∞,-2)）

变式2若函数f(x)=ax3-3x2+1 有两个零点，求a的取值范围.（答案：{0,2,-2}）

变式3若函数f(x)=ax3-3x2+1 有三个零点，求a的取值范围.（答案：(-2,0)⋃(0,2)）

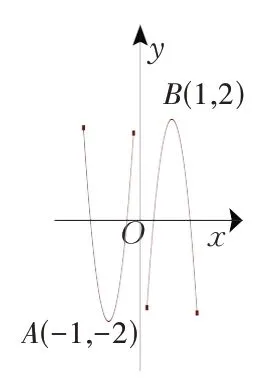
图5

例4已知函数f(x)=(x-1)ex-，若函数f(x)有两个零点，求实数a的取值范围.

解析（分离参数法）若函数f(x)有两个零点，即方程f(x)=(x-1)ex-=0 有两个根.又f(0)=-1，所以0 不是方程f(x)=0 的根.当x≠0时，易知a=也即方程a=有两个根.令g(x)=，也即直线y=a与函数y=g(x)的图象有两个交点.易求 得g′(x)=令g′(x)＞0，得x＞0；令g′(x)＜0，得x＜0.所以函数g(x)在(-∞,0)内单调递减，在(0,+∞)内单调递增，且g(1)=0，又函数g(x)在(-∞,0)内的值域为(-∞,0)，在(0,+∞)内 的值域为R，所以要使直线y=a与函数y=g(x)的图象有两个交点，则a＜0.即当a＜0 时，函数f(x)有两个零点.如图7所示.

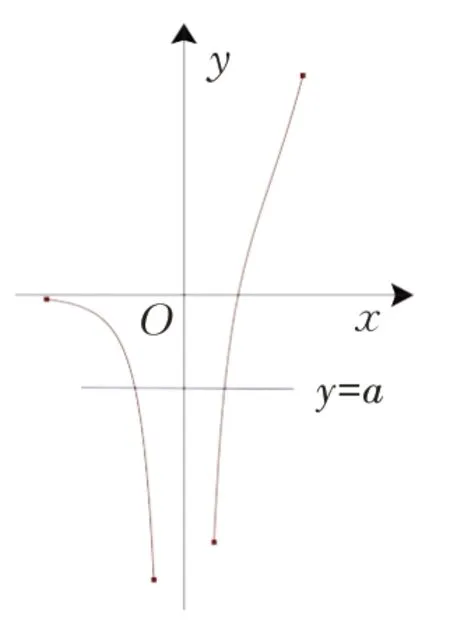
图7

点评如图7 所示，当x→-∞时，y→0，函数图象在x轴下方无限逼近x轴负半轴，即x轴为函数图象的一条渐近线，忽略这一点极易犯错.另外，问题还可变式为判断函数f()x有一个零点时实数a的取值范围.

变式若函数f()x=x2ex-a恰有一个零点，则实数a的取值范围是是（）.

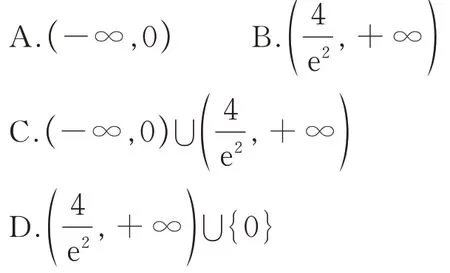
点评如图8 所示，当x→-∞时，y→0，函数图象在x轴上方且无限逼近x轴负半轴，即x轴为函数图象的一条渐近线，忽略这一点极易犯错.另外，本问题还可变式为判断函数f()x有两个零点或没有零点时实数a的取值范围.还有，本试题解答中易漏掉实数a的取值范围中的0.

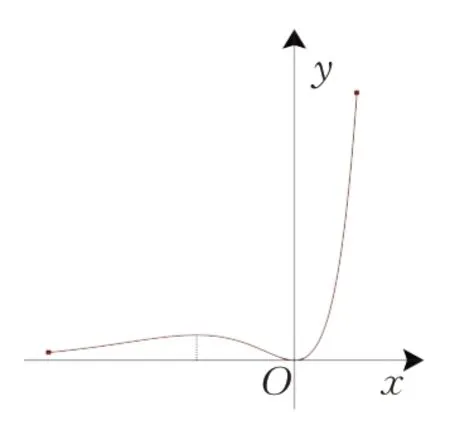
图8

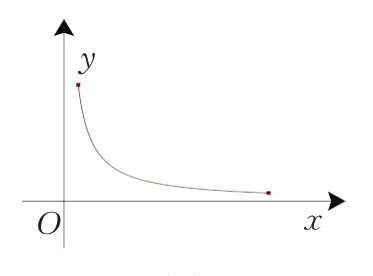
图9

由上述实例不难看出，试题中经常出现以考查指数函数、对数函数及幂函数图象的渐近线问题，而它就像一个“幽灵”，我们很容易忽略它而它又让你防不胜防，一不小心就会受到它的“致命一击”！特别是函数的图象经过平移后渐近线不再是x轴或y轴，而是另一条水平线或竖直线；另外，当出现它们的一些组合式时，更容易犯错，应特别引起重视，如例2中：x∈(1,+∞) 时，＞0；例3 中，当x＞1 时，＞0；当x＜-1 时，g(x)=＜0；例4 中，当x＜0时，g(x)=＜0 等等.

当一类错误经常发生时，我们要去反思错误产生的根源在哪里，从而在解题中引起重视.由本文可知，在解决求参数取值范围等问题时我们通常要借助函数图象来解决问题，而此时极易出现因为函数图象中的“幽灵”（渐近线）而犯错的现象.只要我们在学习中正视错误，剖析问题存在的原因，小心提防错误的发生，仔细观察函数图象的变化，那么“幽灵”一定会离我们远去！