新课程背景下的高中数学题根教学

广东省中山市实验中学 刘 强 （邮编：528400）

2017 年12 月，教育部组织修订并颁布了《普通高中课程方案和语文等学科课程标准（2017 年版）》（简称新课程），从2022 年秋季学期起，全国各省（区、市）均启动实施新课程新教材.新课程对高中数学内容进行了削枝强干，删去了算法初步、推理与证明、程序框图、简单的线性规划问题、三视图等内容，突出函数、几何与代数、统计与概率三大知识主线.新课程重视数学应用，在新教材中设计了大量数学建模和数学探究活动.新课程强调数学文化的渗透，在新教材的正文和阅读材料中有大量的文化背景知识.为了适应新时代的要求，笔者将题根引入课堂，借助题根突破重难点题型，引导学生围绕题根开展探究活动等，取得了不错的效果.

1 题根简介

黄坪和尹得好老师在《高中数学题根》一书的封面上有一句话“记单词想词根，解难题找题根”，这给了题根一个形象的类比.他们还对题根进行了描述性的定义，认为题根是一个题族的根祖，一个题系中的根基，一个题群中的代表.抓到了一个题根，就等于抓到了这个题族，这个题群，这个题系.

上述的描述性定义可以借助集合论的语言进行抽象.题根是某个问题的根源，是一类问题的共同特征.每个题根都对应一个问题集，此集合中的每个题目都具备某共同特征，这个共同特征就是我们所说的题根.但由于共同特征表达起来过于抽象，不容易理解，为了直观通常从这个集合中选取一个典型来代表题根.例如错位相减法求一类数列的前n项和是一个题根，但直接用语言来描述错位相减法的适用条件、操作步骤和注意事项等，会让大多数人看得一头雾水、不知所云.而举个具体的例子大家就知道错位相减是怎么一回事了.因此题根是一类问题的共同特征，但常常以问题的形式出现.

方亚斌老师在《一题一课.源于课本的高考数学题赏析》中描述，许多高考题往往源于课本有关例（习）题，而又高于课本有关例（习）题，即在课本中往往能够找到高考题的题源.因此课本中的一些典型例题、典型习题、典型方法，就是某类题目的“题根”.著名数学教育家张奠宙先生在《数学教育“中国路”》一书中专门提到“题根教学”，评价道：“如果积以时日，寻求‘题根’与变式，也许会成为中国数学教育的又一抹亮色.”

2 高中数学题根教学的常用模式

2.1 专题式

专题式教学是围绕某个题根进行各种变式扩展，旨在一次课讲透一类问题，能增加教学深度，适用于讲解重要题型或重要方法时.方亚斌老师著作的《一题一课.源于世界数学名题的高考题赏析》《一题一课.源于课本的高考数学题赏析》《一题一课.源于中华传统数学文化的高考题赏析》是一个系列，此系列是运用题根进行专题式教学的典范.每篇都是从一道高考题引入，分析背景、觅其源流、挖掘题根，并进行多角度的延伸演变得到变式题组、题链.在平时教学中，善用题根进行专题式教学往往能起到事半功倍的效果.

2.2 渗透式

受限于教学进度的要求，在日常教学中不可能大量进行专题教学，有些重要知识与方法也很难一蹴而就，因此在教学中还经常采用渗透式.以二次函数求最值为例，它的身影出现在高中学习的各个地方，不仅能求解一类基本不等式问题，还可以通过换元法与各类函数结合在一起.再比如投影向量，最早出现在平面向量数量积，在应用空间向量求解立体几何中的距离问题时又大显身手，平面解析几何中的点到直线的距离公式也是用投影向量证明最简单.

3 数学题根在教学中的价值

3.1 题根是解决难题的有力武器

正如黄坪和尹得好老师所说的“记单词想词根，解难题找题根”，题根概念的提出就是为了方便解题.题根可以帮助学生有效地避开误区，快速找到正确的解题思路.

例1（2008 年高考江苏卷）满足条件AB=2,AC=BC的△ABC的面积的最大值是___.

分析这道题从表面上看怎么看都是一道解三角形的问题，但是如果用正余弦定理去做就会落入命题人的圈套，运算十分复杂.这道题的题根是“阿波罗尼斯圆”，学生如果了解“平面内到两定点距离之比为常数的点的轨迹是圆”这个结论，就可以迅速求解此题.

解如图1，以AB的中点为原点，AB所在直线为x轴建立坐标系，很容易得到点C的轨迹方程为：(x-3)2+y2=8.

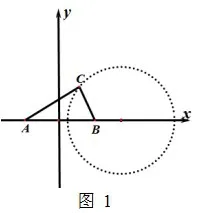
图1

点C到x轴距离最大值为，此时△ABC面积最大,

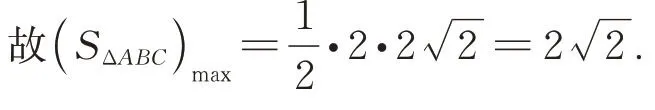
例2（2020 年新高考全国卷1（山东）数学）已知椭圆C=1(a＞b＞0)的离心率为，且过点A(2,1).

（1）求C的方程：（2）点M、N在C上，且AM⊥AN，AD⊥MN，D为垂足.证明：存在定点Q，使得|DQ|为定值.

分析本题单从结果来看，很难入手，因为点Q和点D都不知道，距离|DQ|更是无从表示.本题最关键的条件是AM⊥AN，如果了解题根“过椭圆上一定点做椭圆的两条互相垂直的弦，则两弦端点的连线过定点”，则很容易想到先求MN恒过定点，进而得到下列解法.

解（1）由题意可得椭圆方程为：=1.

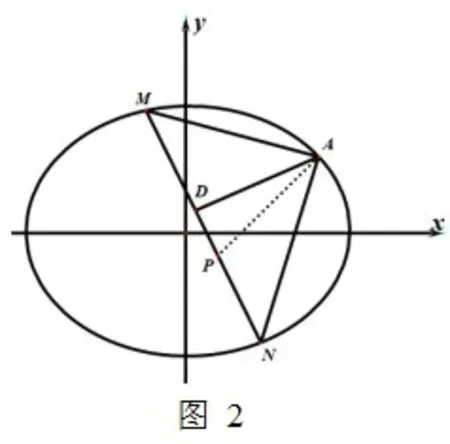
图2

(2) 设点M(x1,y1),N(x2,y2)，直 线MN的方程为：y=kx+m，代入椭圆方程消去y并整理得(1+2k2)x2+4kmx+2m2-6=0，

整理化简得(2k+3m+1)(2k+m-1)=0，

因为A（2,1）不在直线MN上，所以2k+m-1 ≠0，故2k+3m+1=0，

3.2 题根是题型分类的主要依据

数学题目浩如烟海，永远也做不完，但数学题型是有限的.在教学中对题目进行合理分类，可以降低学生理解难度，提高教学效率.题型分类的方式有很多，依据题根进行分类是很有效的一种.因为一类题目都属于同一题根，有相似的解法，便于学生深入理解.以基本不等式求最值为例，这部分内容在新教材里作为预备知识出现.因为题目千变万化、技巧性强，学生学起来很吃力.但如果从题根角度来看，这部分的题根只有两个：二次函数型最值与对勾函数型最值.

再比如圆锥曲线定点问题，除了上面的例2，还有如下题型：

例3（2020 年全国新课标1卷理科）

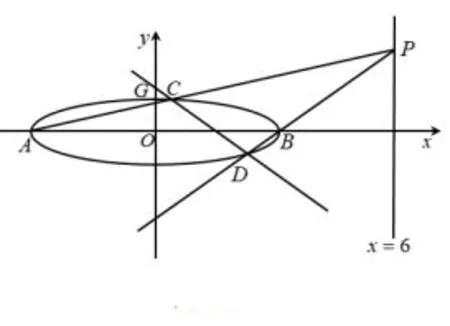
图3

已知A、B分别为椭圆E:+y2=1(a＞1)的左、右顶点，G为E的上顶点=8，P为直线x=6 的动点，PA与E的另一交点为C，PB与E的另一交点为D.

（1）求E的方程；（2）证明：直线CD过定点.

这两题虽然都是定点问题，但题根完全不同.本题的题根是极点极线问题，最佳处理方法是先猜后证.如果不了解题根就会笼统地把它们归为定点问题，不能反应各自的本质.因此，根据题根可以把圆锥曲线的定点问题分为内接三角形类和极点极线类.

3.3 题根是数学建模的强大助手

高中数学人教版新教材十分重视数学知识在实际生活中的应用，将数学建模与数学探究活动作为4 条主线之一.如何培养学生的数学建模和探究能力是数学教学的新课题，在实际教学中笔者发现运用题根思想可以帮助学生提高数学建模的能力.因为，运用数学知识去解决各类实际问题时，首先需要将它转化成为一个数学问题，建立数学模型，然后完成数学模型的解答，最后回归为实际问题的解答.这个数学模型就是一类问题的根源，建模的过程就是寻找根源的过程.

例4如图4，在宽8 米的矩形教室MEFN正前方有一块长6 米的黑板AB，学生座位区域CEFD距黑板最近1米，在教室左侧边CE上寻找黑板AB的最大视角点P（即使∠APB最大），则CP=______时，∠APB最大.

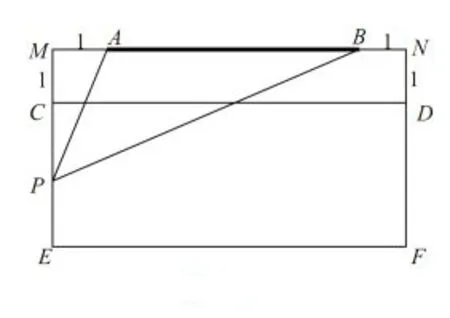
图4

例5如图5 所示，某人在一山坡P处观看对面山项上的一座铁塔，塔高BC=80（米），塔所在的山高OB=220（米），OA=200（米），图中所示的山坡可视为直线l且点P在直线l上，l与水平地面的夹角为α，tanα=，试问此人距水平地面多高时，观看塔的视角∠BPC最大.

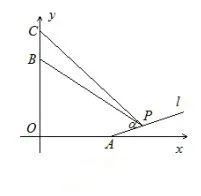
图5

分析这两道题都属于最大视角问题，可以由正切函数结合基本不等式求解，但计算量较大.如果了解这类问题的题根，则很容易建立合适模型，轻松得到解答.

题根（米勒定理）如图6，设M、N是锐角∠ABC的一边BA上的两定点，点P是BC边上的一动点，则当且仅当△PMN的外接圆与边BC相切时，∠MPN最大.

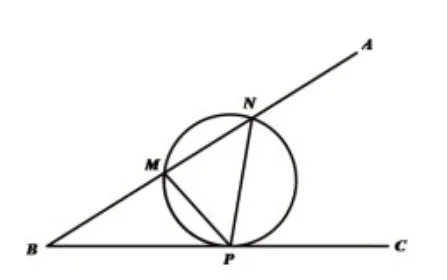
图6

解答如图7，延长AP交y轴于点M，由已知可得OM=100.由切割线定理知MP2=MB·MC=320×400=12800，所以MP=,AP=MPMA=，可得P点坐标为P(320,60).

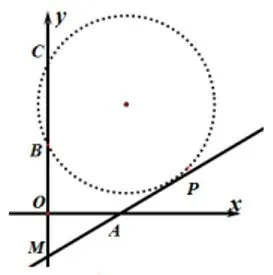
图7

故当此人距水平地面60 米高时，观看铁塔的视角∠BPC最大.

3.4 题根是数学探究的基本方向

数学探究即数学探究性课题学习，是指学生围绕某个数学问题，自主探索、学习的过程.与数学建模不同，数学探究是数学知识在数学内部的联系和应用，而数学建模是数学知识在数学外部的应用.要想提高学生的探究能力，需要老师适当引导，让学生去自主探索数学知识之间的联系和应用.在探究过程中如果了解一类问题的题根，将会为探究活动指明方向.

例6如图8，放置的正方形ABCD，AB=2，A、D分别在x轴、y轴上滑动，求的最大值.

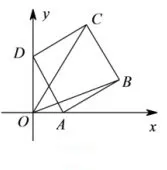
图8

分析本题看似是一道简单的数量积问题，但如果设∠ODA=θ，然后用θ表示四个顶点，则很容易得出错误解答，因为正方形在不同象限时，点的表达式是不同的.这就需要老师引导学生去探究题目的根源.

问题1当AD移动时，∠AOD有什么特点？

问题2如果让正方形不动，你能求出O点的轨迹吗？

通过上述引导，可以让学生发现：无论AD如何移动，∠AOD都是直角，也就是说O点落在以AD为直径的圆上.根据相对运动的思想，可以把正方形固定，让O点运动，则O点的轨迹是以AD为直径的圆，由圆的参数方程可得以下解法.解如图9，建立新的 坐 标系，可得A(1,0)，D(-1,0)，B(1,2)，C(-1,2),O(cosθ,sinθ)，则=(-1-cosθ,2-sinθ),=(1-cosθ,2-sinθ)=-1+cos2θ+4-4 sinθ+sin2θ=4-4 sinθ.

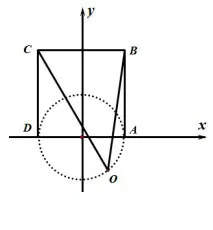
图9

故当θ=时取得最大值8.

变式1等边三角形ABC的边长为2，A、B两点分别在x轴、y轴上滑动，P、Q分别为AC、BC的中点，求的取 值范围.

变式2矩形ABCD的顶点A、D分别在x轴、y轴滑动，其中AD=2,AB=1，求的取值范围.

通过探究，可知这类问题的题根是圆的参数方程，运用了相对运动思想.这种探究可以让学生学会不能被题目的表象所迷惑，感受数学知识间的联系与应用.

3.5 题根是数学文化的传播途径

在漫长的数学发展史中，形成了无数的数学文化瑰宝，例如赵爽弦图、杨辉三角、祖暅原理、秦九韶公式、鳖臑阳马等等.每一个文化瑰宝都是一个题根，为了充分展示它们的魅力，可以借助题根的渗透性，围绕它们进行各种变式，与高中数学各知识点结合，渗透到日常教学中去.下面以赵爽弦图为例.

例7（与三角结合）“赵爽弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形（如图10），若大、小正方形的面积分别为25 和1，直角三角形中较大的锐角为θ，则cos 2θ=_________.

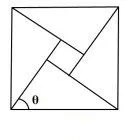
图10

例8（与向量结合）受“赵爽弦图”启发，某同学设计了一个图形，该图形是由三个全等的钝角三角形与中间的一个小正三角形拼成的一个大正三角形，如图11所示，若AD=4，BD=2，那么=______.

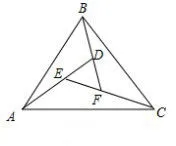
图11

例9（与数列结合）第24届国际数学家大会会标就是以“赵爽弦图”为基础进行设计的.如图12，四边形A1B1C1D1是由四个全等的直角三角形与一个小正方形ABCD拼成的一个大正方形.如果小正方形ABCD的面积为1，再以正方形A1B1C1D1为“小”正方形向外作“弦图”，得到正方形A2B2C2D2……按此做法进行下去，记∠AA1B1=θ，)，正方形An BnCn Dn的面积为an(n∈N*).若tanθ=则an=________.

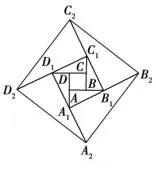
图12

可见，题根有强大的生命力，可以在数学教学的方方面面发挥重要作用.研究数学题根不仅对老师在教学和解题方面有重要意义，还能帮助学生跳出题海、深入理解数学内涵进而发展学生核心素养.在数学教学中，如果能根据新课程的特点，充分发挥题根教学的优势，一定能成为教育的又一抹亮色.