群钉连接组合轨道梁刚度调整系数研究

周帅，于鹏，聂建国，罗桂军，张胥，张欢*

（1.中国建筑第五工程局有限公司，湖南 长沙410004；2.清华大学 土木水利学院，北京100084）

跨座式单轨交通占地小，适应地形能力强，节能环保，观光效果好，在中国二三线城市和“一带一路”沿线的中小城市具有广阔的应用前景[1-2]。跨座式单轨交通车辆抱轨运行，轨道梁既是承重结构，又是走行轨道，如图1所示。成桥线形精度要求高。采用基于群钉连接的钢-混组合轨道梁结构形式，可实现轨道梁下部钢箱和上部混凝土板的标准化拆分、工厂化预制、装配化施工，解决传统混凝土轨道梁毫米级成桥线形精度控制难度大、纯钢梁运营振动噪声等问题，同时也可以合理应对满铺剪力钉现浇混凝土组合梁收缩裂缝等隐患。

图1 跨座式单轨交通Fig.1 Straddle monorail transit

群钉连接钢-混组合轨道梁为部分剪力连接结构，存在无钉区刚度不连续和界面滑移的问题，导致其竖向刚度和界面无滑移与理想状态有一定区别，甚至存在平截面假定适用性问题，该问题目前尚缺乏研究。徐国平等人[3-4]基于弹性地基梁理论和塑性发展系数提出了一种确定满铺剪力钉抗剪连接件的刚度和承载力的方法，针对部分抗剪组合梁群钉效应的研究和应用仍相对较少。张永康等人[5]综述了滑移效应对钢-混凝土组合梁的影响。范亮等人[6-7]对装配式群钉组合梁与现浇组合梁进行了对比试验研究。王宏亮[8]研究了考虑滑移效应的悬挂式单轨钢混组合轨道梁-车辆耦合系统动力特性及低频噪声问题。项怡强等人[9-14]对钢-混凝土组合梁长期滑移及其影响进行了深入研究。

考虑到跨座式单轨交通桥跨结构通常由竖向刚度控制设计且对竖向自振频率较为敏感，在分析并修正界面滑移时带来的计算偏差。本研究根据钢-混凝土组合结构界面无滑移刚度理论，建立群钉连接组合轨道梁理论基础，结合挠度试验结果，得出对应的刚度调整系数，并通过静力试验、动力试验得出应变和自振基频，验证刚度调整系数的准确性和适用性。

1 理论基础

针对界面无滑移钢-混组合梁，以钢材作为等效弹性模量基准：

Eeq=Es。 （1）

式中：Eeq、Es分别为等效弹性模量和钢材弹性模量。

无滑移组合梁轴向刚度为：

Eeq·Aeq=Es·As+Ec·Ac。 （2）

式中：Aeq、As、Ac分别为等效截面积、钢箱截面积和混凝土板截面积；Ec为混凝土弹性模量。

无滑移组合梁中性轴与轨道梁走行面距离为：

式中：Hs、Hc分别为钢箱、混凝土板截面形心与轨道梁走行面距离。

无滑移组合梁弯曲刚度为：

Eeq·Ieq=Es·Is+Es·As·(Ls-Leq)2+

Ec·Ic+Ec·Ac·(Lc-Leq)2。 （4）

式中：Ieq、Is、Ic分别为等效截面惯性矩、钢箱惯性矩和混凝土板惯性矩。

根据材料力学公式，以简支为边界条件，在跨中集中力F下，跨径L的界面无滑移组合梁的跨中竖向挠度为：

ω1=FL2/(48Eeq·Ieq)。 （5）

若试验实测或精细化实体有限元模型的竖向挠度为ω2，定义竖向刚度调整系数α为：

α=ω2/ω1。 （6）

考虑竖向刚度调整系数α后，即可计算界面有滑移组合梁截面任意位置的应力σ、应变ε：

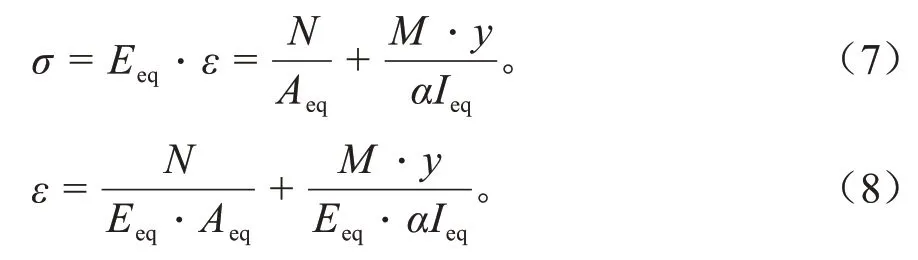
式中：M、N分别为截面弯矩和轴力；y为截面任意位置与中性轴距离。

滑移组合梁跨中钢箱处任意点应力σs为：

滑移组合梁跨中混凝土板任意点应力σc为：

根据《公路桥涵设计通用规范》(JTG D60-2015)，计算滑移组合梁自振基频为：

2 模型试验

2.1 试验模型与参数

跨座式单轨交通双线群钉连接钢-混组合轨道梁原始设计参数如下：

①断面参数

双线线间距4.6 m，简支50 m跨径双线钢-混凝土组合轨道梁梁高3.1 m，上部混凝土板厚度32 cm，宽度69 cm，下部钢箱高度278 cm。

②平面参数

群钉槽口尺寸为21 cm×90 cm，纵向中心距2 700 cm，横向错位布置，降低“无钉区”长度。

本研究根据该原始设计参数，制作了1∶3的缩尺试验模型，其断面如图2所示。

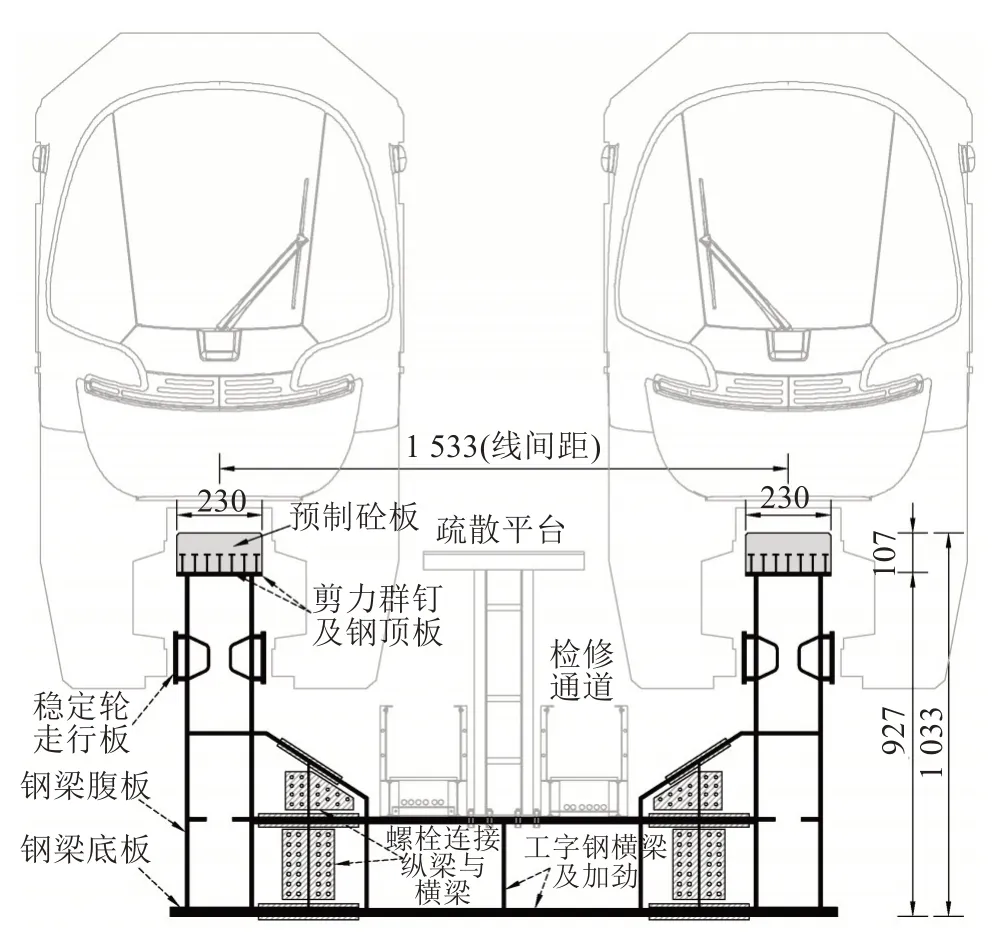
图2 轨道梁缩尺模型断面（单位：mm）Fig.2 Scale model section of track beam(unit:mm)

2.2 装配前钢箱梁（钢梁）模型

剪力群钉在设计指定位置与钢箱焊接，混凝土板按设计位置尺寸预留槽口如图3～4 所示。组合轨道梁混凝土板在工厂预制、养生完成后，运至现场与下部钢箱梁群钉对孔装配，后浇槽口，实现钢箱-混凝土板组合。

图3 钢梁Fig.3 The steel beam

图4 预制混凝土板Fig.4 The precast concrete slab

2.3 装配后钢-砼组合梁（组合梁）模型

预制混凝土板养生完成后，运输至钢梁吊装与剪力群钉对孔装配，后浇群钉槽口高性能混凝土，形成界面有滑移的钢-混凝土组合群钉轨道梁，如图5所示。

图5 预制混凝土板吊装Fig.5 The hoisting of precast concrete slab

2.4 静力试验

试验组合梁简支支撑在地面台座上，通过试验机进行跨中单侧集中荷载加载。梁底设置接触式位移计与千分表，测试梁底的竖向变形，沿双线组合梁左、右两幅的跨中、梁端、四分点均设有测量点位，共计20个点位。

混凝土板与钢梁之间设置传感器，分别测量荷载作用下跨中、支座、预制板湿连接处、两侧剪力槽边缘处混凝土板与钢梁截面的滑移值，如图6所示。沿着组合梁截面高度设置应变片，测量截面高度应变数据，观察荷载作用下下部钢梁和上部混凝土板在同一截面的变形协调特征，如图7所示。

图6 组合界面滑移测试Fig.6 The slip test of composite interface

图7 混凝土应变测试Fig.7 The strain test of precast concrete slab

2.5 动力测试

梁体放置于实验室平整地坪上，梁端底部通过临时滚轴支座支撑地面，梁端可以扭转自由度，约束三向平动自由度，模拟简支边界条件，如图8所示。测试所用传感器为拾振器，采样频率为1 000 Hz。

由于梁体较重，加载位置空间与技术受限，采用环境振动的方式收集原始数据，分析处理得到固有频率和阻尼比等动力特性参数。

图8 组合梁动力特性测试Fig.8 Dynamic characteristic test of the composite beam

3 有限元计算

3.1 有限元简化模型

采用Midas Civil 对试验模型进行有限元分析，如图9所示。其中，全桥钢纵梁、加劲肋及混凝土板基于平截面，假定采用同一个组合截面，并按梁单元模拟，横梁与纵梁间采用刚臂连接，全桥共划分为150个单元。

图9 Midas Civil简化模型Fig.9 Midas Civil simplified model

3.2 有限元精细模型

为模拟群钉连接组合梁界面滑移特性，采用Midas FEA 对试验模型进行有限元分析。其中，全桥钢纵梁、横梁、横隔板、稳定轮走行板、加劲肋均采用厚板单元，完全按实际位置和尺寸模拟。混凝土板采用实体单元模拟。剪力钉采用非线性弹簧模拟，弹簧参数取自基于推出试验所选的“荷载-位移”曲线。支座范围内，板单元设置刚域，支承于支座中心节点，全桥共划分为179 556个厚板单元、156 000个实体单元，如图10所示。

图10 Midas FEA精细模型Fig.10 Midas FEA detailed model

4 结果与分析

4.1 刚度调整系数

集中荷载作用在组合梁跨中位置的顶面，提取轨道梁梁底竖向位移值作为组合梁最大挠度实测结果（实测值），荷载等级以100 kN 为间隔，加载到800 kN 时，作用点混凝土局部压碎破坏，组合梁丧失协同变形能力，梁底最大竖向挠度达到27.5 mm。经比较，Midas Civil 简化模型与式（5）均未考虑界面滑移，两者获得的挠度值结果一致，可作为理论值。Midas FEA 精细模型考虑了群钉和界面滑移效应，所得结果作为计算值，与试验实测挠度值接近。采用式（6）计算不同荷载等级下竖向刚度调整系数α理论=ω理论值/ω实测值和α计算=ω计算值/ω实测值，对比如图11所示。

图11 理论与计算刚度调整系数的对比Fig.11 Comparison of theoretical and calculated stiffness adjustment coefficients

从图11 中可以看出，基于理论值和计算值所得的刚度调整系数均随荷载的变化而变化。同一等级荷载作用下，计算刚度调整系数大于理论刚度调整系数。试验实测荷载-刚度调整系数曲线呈现非线性特征，存在1 个反弯点，以200 kN 荷载作用点为界。低荷载作用下，理论刚度调整系数和计算刚度调整系数随试验荷载增大而增大，且均大于1（最大值为α计算=1.143）。高荷载作用下，理论刚度调整系数和计算刚度调整系数则随试验荷载增大而减小，最终均减小到1以下（最小值为α理论=0.898）。

4.2 频率分析和对比

钢梁、组合梁的竖向自振基频率结果对比见表1。其中，理论值的刚度调整系数按式（11）和有限元简化模型计算，计算值为有限元精细模型计算结果[15-17]，实测值为根据传感器实测数据分析结果。由于环境振动识别方法为小幅荷载激振，组合梁刚度调整系数选用100 kN 加载试验对应的值。考虑到纯钢梁为规则结构，其刚度调整系数取1.0，即未做调整。

表1 理论、计算和实测基频的对比Table 1 Comparison between theoretical frequency,calculated frequency and measured frequency Hz

从表1中可知：

1）对于纯钢梁，未进行刚度调整的自振基频理论值、计算值与实测值基本一致。因为纯钢梁截面沿纵向基本上为同一值，其抗弯刚度也几乎无变化，故直接采用理论公式和简化模型计算即可得到非常精确的频率解。

2）对于组合梁，混凝土板与钢梁群钉连接后，提高了截面抗弯刚度，也增加了等效质量，因抗弯刚度增加后对频率的影响大于等级质量，故组合后频率有所提高。相比与混凝土板组合前纯钢梁频率的理论值、计算值和实测值，基于刚度调整系数修正后的组合梁频率分别提高了4.4%、7.4%、7.7%。

3）组合梁频率的实测值略高于理论值和计算值，由于预制混凝土板与钢梁的表面接触、摩擦等因素，提高了梁体非线性刚度，而环境振动这种小幅荷载激励无法消除影响，使得实测结果偏大。

4）基于刚度调整系数的理论公式和简化模型，计算得到群钉连接组合梁频率与试验实测值的误差为2.2%；基于刚度调整系数的精细模型其误差则为4.0%，两者均可用于类似结构设计前期阶段的快速比选和后期细化设计时的构造定型。

4.3 应力分析和对比

组合梁跨中截面不同荷载等级作用下，根据α理论和α计算得到沿截面各高度处钢梁、混凝土板的应力，再与拟合后实测值进行对比，如图12所示。从图12中可以看出：

1）不同加载工况下，根据α理论和α计算得到理论应力值和实测应力值，拟合后，发现3种结果对应的中性轴基本一致，均在561～600 mm 范围内。中性轴随着荷载值的增大有所抬高，中性轴以上钢梁和混凝土板均受压，中性轴以下钢梁受拉。

图12 理论与计算应力与实测应力的对比Fig.12 Comparison of theoretical stress,calculated stress and measured stress

2）100 kN荷载下，混凝土板最大压应力理论值、计算值和实测值分别为－4.9、－5.3、－5.8 MPa，均满足桥梁规范限值－26.5 MPa，理论值、计算值与实测值的相对误差分别为15.5%、8.6%。200 kN荷载下，混凝土板最大压应力理论值、计算值、实测值分别为－10.7、－11.7、－13.2 MPa，理论值、计算值与实测值的相对误差分别为18.9%、11.4%。可见随着荷载加大，理论值、计算值与实测值的相对误差有所增大，反映了大幅荷载下混凝土板整体受力非线性特性更为显著。

3）100 kN 荷载下钢梁最大拉应力理论值、计算值、实测值分别为39.3、35.2、32.6 MPa，均满足桥梁规范限值275 MPa，理论值、计算值与实测值的相对误差分别为20.6%、8.0%。200 kN荷载下混凝土板最大压应力理论值、计算值、实测值分别为85.3、75.7、68.9 MPa，理论值、计算值与实测值的相对误差分别为23.8%、9.9%。表明：由于混凝土板非线性变形导致钢结构受力产生了相应的非线性变化，随着荷载加大，钢梁应力的理论值、计算值与实测值的相对误差有所增大，其误差增幅与混凝土板的接近。

4）钢混交界面以下，钢梁的实测应变沿截面高度方向呈线性关系。钢混交界面以上，混凝土板与钢梁的实测并非线性关系。以200 kN 加载为例，交界面处混凝土板底缘的实测应变值（－4.43×10－5）小于钢梁顶缘的（－8.25×10－5），而混凝土板顶缘实测应变值（－1.62×10－4）大于钢梁顶缘的（－8.25×10－5），混凝土板与钢梁的变形不协调，与平截面假定（按基于α理论计算的交界面应变值为－9.94×10－5）存在一定差别。表明：混凝土板提前介入受力，在组合梁等效刚度中发挥了更多作用，在一定程度上可以解释刚度调整系数非线性的问题。

5）基于刚度调整系数的理论公式和简化模型，计算该群钉连接组合梁时与实测值的应力误差为15.5%～23.8%；基于刚度调整系数的精细模型其误差为8.0%～11.4%。前者可用于类似结构设计前期阶段的快速比选，后者可用于后期细化设计时的构造定型。

5 结论

1）基于理论分析、有限元计算、试验实测所得的刚度调整系数均随荷载的变化而变化。同一等级荷载作用下，计算刚度调整系数大于理论刚度调整系数。试验实测荷载-刚度调整系数呈现非线性特征，存在1个反弯点。低荷载作用下，理论和计算刚度调整系数随试验荷载增大而增大，且均大于1。高荷载作用低荷载作用下理论刚度调整系数和计算刚度调整系数随试验荷载增大而减小，最终均减小到1以下。

2）基于刚度调整系数修正群钉连接组合梁理论，竖向弯曲固有频率与试验实测值的偏差为2.2%，有限元精细模型计算结果偏差为4.0%，两者均可用于类似结构设计前期阶段的快速比选和后期细化设计时的构造定型。

3）基于刚度调整系数修正群钉连接组合梁理论，应力结果与试验实测值偏差为15.5%～23.8%，有限元精细模型计算结果偏差则为8.0%～11.4%。应力结果理论值、计算值与实测值对应的中性轴均在561～600 mm 范围内，随着荷载值的增大，中性轴有所抬高，前两者与实测值的相对误差有所增大。群钉连接组合梁截面受力不完全满足平截面假定，大幅荷载作用下混凝土板整体受力非线性特性更为明显。