碳纤维加固二次受力混凝土梁理论计算方法

钟正强，陈敬智，刘卓泽

（长沙理工大学 土木工程学院，湖南 长沙410114）

钢筋混凝土梁广泛应用于中国民用建筑和中小型城市桥梁主体结构中。由于车流量增大，部分旧桥受损严重[1]，已经不能满足设计规范的要求。加固规范[2]明确指出：碳纤维材料加固受弯构件承载力计算需充分考虑二次受力带来的影响。因此，本研究从抗弯构件的角度出发，通过对比理论计算值和试验结果，研究二次受力对碳纤维网格-聚合物砂浆复合加固梁极限承载力和挠度的影响规律，有效提高了碳纤维加固梁挠度和承载力计算预测的精度。

当前，许多学者在受弯构件理论计算方面开展了大量推导研究。唐浩杰等人[3]对预应力混凝土箱梁进行受弯破坏试验，采用有限条带法计算了开裂与破坏弯矩，与试验结果较为吻合。潘毅等人[4]提出了碳纤维增强复合网格-聚合物水泥砂浆加固RC 梁的抗弯承载力改良计算模型。江世永等人[2，5]指出现有加固规范缺少对加固梁变形控制验算的有效方法，不能准确判断加固梁在使用阶段内是否满足正常使用极限状态的要求。因此，提出了一种在设计阶段对加固梁进行挠度计算的方法。出于安全考虑，对加固梁承载力和挠度进行折减，能有效提高计算效率。但该方法对不同系数的取值欠缺考究，影响计算的准确性。因此，本研究从混凝土本构模型出发，对加固梁承载力和挠度计算公式进行推导，并考虑了不同参数的取值方法。

1 CFRP加固梁抗弯承载力计算方法

1.1 基本原理

选取碳纤维网格加固梁跨中截面进行分析，受压区混凝土采用规范中混凝土应力-应变曲线[6]，如图1 所示。在图1(c)中，对受压区混凝土截面应力积分，可得合力C，以及合力到中和轴的距离yc为：

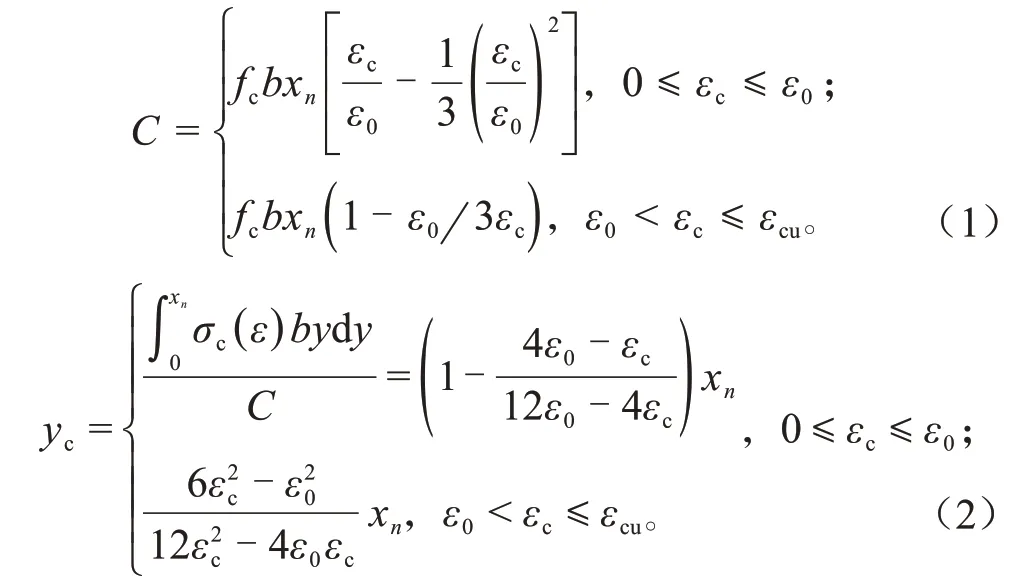
式中：fc为极限抗压强度；εc为混凝土压应变；ε0为达到极限抗压强度时的应变；εcu为极限压应变；σc为混凝土；b为梁宽；xn为中和轴高度。

混凝土受压区采用等效矩形应力法[7]，由合力作用点位置不变，可得等效高度x为：

x= 2(xn-yc) =β1xn。 （3）

其中，

由截面力平衡条件可得：

由平截面假定[8]确定截面几何关系，可将式（5）化归到只含有变量εc和xn的方程：

Ax2n+Bxn+C= 0。 （6）

式中：A=C/xn；B=εcEsA′s0+εcEsAs0+εcEfAfe+

由弯矩平衡条件和截面几何关系，对截面混凝土受压区合力作用点取距，可得：

其中，

式中：εc为钢筋混凝土梁梁顶压应变；εs1为碳纤维网格带后应变；As0、A′s0、Afe为纵向受拉、受压钢筋和CFRP 网格的截面有效面积；d为找平砂浆层厚度；a′s为梁顶距受压钢筋的高度；h为加固梁梁高；h0为梁顶距碳纤维网格高度；h1为梁顶距受拉钢筋高度；Es、Ef为钢筋和CFRP 网格的弹性模量。

根据式（8）得到M- εc关系，推导出M-xn、M-β1等关系，用于后续挠度计算。

1.2 计算流程

由加固规范可知，抗弯构件梁二次受力引起的纤维复合材料滞后应变[2，8]为：

破坏类型一：钢筋屈服，受压区混凝土压碎。

εc=εcu。 （10）

将式（9）～（10）分别代入式（4）和式（7），可得β1和xn。再代入式（3），可计算得出x，再将x和xn代入式（7）～（8），得出受压区混凝土压碎破坏状态下加固梁的抗弯极限承载力。

破坏类型二：加固梁钢筋屈服，CFRP 网格布拉断破坏，有εc≤εcu，Δεs=εfu。

由截面几何关系可得：

1.3 破坏现象判断

钢筋混凝土加固梁相对界限受压区高度：

同时发生碳纤维拉断与受压区混凝土压溃时的相对界限受压区高度：

用式（11）代替式（10），计算流程同破坏类型一，即可得出CFRP 网格拉断破坏状态下加固梁的抗弯极限承载力。

当x＜ξ′b( )h0+d时，加固梁破坏类型为碳纤维网格拉断破坏；当ξ′b( )h0+d＜x＜ξbh1时，破坏类型为受压区混凝土压溃破坏；当x＞ξbh1时，受拉钢筋未屈服，破坏类型为超筋破坏。

图1 加固后矩形截面梁正截面应力应变Fig.1 The stress and strain on the normal section of the reinforced rectangular section beam

2 CFRP加固梁挠度计算方法

钢筋混凝土梁刚度计算方法主要分为有效惯性矩法、刚度解析法和受拉刚化效应修正法[9]。本研究主要参考刚度解析法[10]对二次受力下碳纤维网格加固梁的短期刚度进行推导。由弯矩平衡和平截面假定，可得关于受拉钢筋应变εs0的弯矩表达式为：

由式（15）原加固梁截面可转换为单筋矩形截面。参考刚度解析法思路[11-12]，得到短期刚度： 为等效受拉钢筋面积，mm2；η为内力臂系数；ψ为应变不均匀系数。

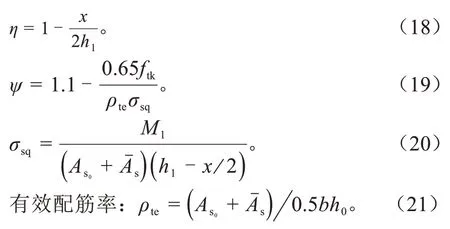
查阅《建筑结构静力计算手册》可知，对于两点对称加载的简支梁，其跨中挠度为：

式中：l为梁的计算跨度，mm；a为加载点到支座的最近距离，mm，α=a/l。

3 理论值与试验值对比分析

3.1 试验方案与设计

为研究二次受力对碳纤维网格加固梁[13-15]抗弯承载力和跨中挠度的影响，本试验设计了4片钢筋混凝土矩形梁，每片梁的尺寸和配筋情况均相同。截面尺寸为：b×h0=120×240 mm，梁长L=2 600 mm，计算长度L0=2 400 mm，高跨比h/L0=240/2 400，剪跨比λ=α/h1=1 000/(240-30)。纵向受力筋采用HRB335 级热轧月牙纹带肋钢筋。其中，架立筋为2Φ12，A′s0=226 mm2，受拉主筋为2Φ18，As0=509 mm2。混凝土强度等级为C40，混凝土保护层厚度为30 mm。试验采用四点弯曲加载方式，以5 kN/级的速率进行加载[16]，加载装置如图2所示。

图2 加固梁加载装置示意Fig.2 Schematic diagram of the loading apparatus of the reinforced beam

本试验对不同加载历程下碳纤维网格-聚合物砂浆复合加固梁进行了对比试验，以期了解二次受力对加固梁抗弯性能的影响，对照组详情见表1。

表1 试验变量设计Table 1 Design of experimental variables

3.2 抗弯承载力结果对比分析

二次受力下碳纤维加固梁的极限承载力与试验值见表2。由表2 可知，施加的预载幅值越大，碳纤维网格的滞后应变越明显，加固梁承载力提高程度随之降低。

3.3 挠度结果对比分析

对荷载-中和轴高度曲线（P-xn）和荷载-等效矩形应力系数的二元方程式进行插值拟合，其关系曲线如图3～4 所示。从图3～4 中可以看出，刚开始受力时，加固梁受压区混凝土处于弹性变形状态，中和轴高度xn随外加荷载的逐级施加呈抛物线型增长。继续加载，受压钢筋开始受力，受压区混凝土应力发生重分布现象，xn发生突变。本研究将P-xn、P-β1分为3 段，采用分段多项式拟合和中间段线性插值的方法，将该曲线应用于加固梁挠度的计算，有效提高了计算的精度和准确性。

表2 理论值与试验值对比Table 2 Comparison of theoretical and experimental values

在挠度计算公式的推导过程中，因没有考虑到砂浆层对加固梁中和轴高度的影响，会对加固梁的短期刚度进行了折减，所以理论计算值相对于实测值有所偏大。从图5～8 中可以看出，通过对比不同预载幅值下的加固梁荷载-挠度曲线可知，预加荷载值越大，聚合物砂浆层拉裂受损越严重，二次受力下砂浆层对加固梁中和轴高度的影响越小，加固梁挠度计算值越接近实测值。

图3 P-xn曲线Fig.3 P-xn curve

图4 P-β1曲线Fig.4 Load-stress coefficient curve

图5 CFN加固参考梁荷载-位移曲线对比Fig.5 Load-displacement curves of CFN reinforced beam

图6 CFN-04加固梁荷载-位移曲线对比Fig.6 Load-displacement curves of CFN-04 reinforced beam

图7 CFN-06加固梁荷载-位移曲线对比Fig.7 Load-displacement curves of CFN-06 reinforced beam

图8 CFN-08加固梁荷载-位移曲线对比Fig.8 Load-displacement curves of CFN-08 reinforced beam

4 结论

1）本研究对二次受力下碳纤维网格加固梁的抗弯承载力计算公式进行了推导，通过计算其相对界限高度来判断加固梁的破坏类型，并采用该类型承载力公式进行求解计算。

2）基于规范中抗弯构件正截面混凝土应力-应变关系式，推导出P-xn、P-β1关系曲线，并应用于加固梁加载全过程挠度计算，计算值与试验结果的契合度较好，有效提高了计算精度。

3）本研究提供了一种计算思路，规避了由等效矩形应力系数β1、内力臂系数η等参数取值带来的求解误差。所有公式不仅限于碳纤维网格加固梁的承载力和挠度计算，对采用碳纤维布、碳纤维板等其他材料的加固梁同样适用。