浅埋小净距隧道围岩压力的极限分析

晏莉，文胜，喻少华，杨海涛，吕超慧

（长沙理工大学 土木工程学院，湖南 长沙410114）

浅埋隧道围岩压力的计算方法主要有：岩柱体结构理论、太沙基理论和规范法等，这些方法都是利用极限平衡法对其进行理论推导。随着极限分析理论的发展，在边坡稳定、地基承载力等领域取得了诸多成果，国内外许多学者也纷纷将其应用于隧道围岩的稳定性分析之中。Davis 等人[1]拟定出了4 种黏性围岩条件下圆形浅埋隧道的破坏模式，并将极限法得到的计算结果与离心机试验结果进行对比，验证了此法的可行性。Pan 等人[2]通过对非圆形隧道破坏模式的研究，利用极限分析上限理论和折减法，推导出非圆形隧道的安全系数。Soubra 等人[3]利用2 种截断的圆锥体刚块构造出一种新的破坏模式，并采用极限分析上限法计算出在压力盾构作用下隧道开挖面的土压力值。Atkinson 等人[4]基于室内模型试验，并运用极限分析理论对浅埋隧道围岩稳定性问题展开了一系列探讨。Takemura 等人[5]针对地表水平的圆形隧道提出了考虑多因素的对称破坏模式。谢骏等人[6]利用4 种单洞圆形隧道破坏模式，构造了考虑土重影响的近邻双孔隧道的破坏模式，推导出双洞隧道围岩压力的上限解，并将计算值与离心试验结果进行对比，验证了该上限解的可行性。姜功良等人[7]通过极限分析理论推导出隧道的稳定性系数，在一定程度上对上限解进行了改良。杨峰等人[8]分析了浅埋隧道工作面维持稳定所需要的支护力，建立了多刚性块的破坏机制和相应的速度场。凌同华等人[9-10]利用FLAC3D数值模拟软件，分析了不同施工顺序和施工方法对小净距隧道围岩稳定性的影响。在软弱围岩中，特别是在土体中，实验表明[11-14]大部分土体都是服从非线性破坏准则。因此，作者拟基于非线性破坏准则，利用极限分析上限定理，建立浅埋小净距隧道的刚性块破坏模式，推导出浅埋小净距隧道围岩压力的半解析解表达式。

1 土体非线性破坏准则

土体的非线性Mohr-Coulomb 准则及其切线表达式为[15]：

式中：σn、τ分别为破坏面上的正应力和剪应力，kPa；σt为轴向拉应力，kPa；c0为初始黏聚力，kPa；ct、tanφ分别为切线表达式的截距及斜率；m为非线性系数。

将式（1）和式（2）联立，解得ct的表达式为：

由切线法原理[16]可知：非线性破坏准则式（1）的上限解可根据式（2）和式（3）联立求解得到。

2 破坏模式及速度场的构建

2.1 破坏模式的构建

根据《公路隧道设计规范第一册土建工程》（JTG 3370.1-2018）[17]中规定，以Ⅴ级围岩为例，当双洞隧道间距大于(2.0～2.5)B时，左、右两洞开挖，岩柱侧产生的滑裂面相交于地表以上，此时认为双洞隧道间几乎不产生影响，左、右两洞围岩压力可按单洞隧道分别进行计算。当双洞隧道间距小于(2.0～2.5)B时，两洞破裂面相交于地表以下，此时两隧道间的影响不可忽略，围岩压力的计算同单洞隧道的不一致。根据该规范[17]，为方便分析计算，对浅埋小净距隧道破坏模式作出简化及假设：

1）将隧道开挖面简化为高h、开挖跨度B的矩形断面，两洞室之间的净距为D，隧道埋深为H。类似的圆形、三心圆洞室也可按此方法进行简化。

2）假设作用在隧道顶部的垂直压力q1、q2呈线性分布，水平围岩压力呈均匀分布，分别为e1、e2，满足条件ei=kqi（i=1、2），考虑两洞呈对称分布，如图1 所示。在图1 中仅绘出左洞围岩压力分布图。

图1 浅埋小净距隧道围岩压力分布Fig.1 Stress distribution in surrounding rock of shallow-buried small spacing tunnel

3）假设地面水平，土体均为连续单一的介质，隧道埋深较浅，应力水平不高，为简化计算，采用线性Mohr-Coulomb屈服准则。

4）由于施工方法和开挖时间对隧道围岩压力有较大影响，为便于分析计算，此处暂不考虑施工方法对隧道围岩压力的影响。

5）杨小礼[18]提出，选择速度场时，尽量使速度场简单，对本研究破裂面进行简化。把实际破裂面划分为2 个小段，将交点首尾相连，用2条折线来代替破裂面，按规范法[17]构建小净距隧道内侧破裂面形状，假定小净距隧道两侧破裂面为对称分布，如图2 所示。在图2 中，α、ω、η为间断线间的夹角。

图2 浅埋小净距隧道破坏模式Fig.2 Failure mode of the shallow-buried small spacing tunnel

2.2 速度场的构建

根据破坏模式可知，由于隧道上部土体ABFG 和FGHIK 存在周围围岩给的水平约束作用，而竖直方向上仅受自身重力影响。由于结构的对称性，认为其速度矢量v0的方向为竖直向下。内外侧边墙处三角形刚性块的速度矢量分别为v1和v2，各刚性块之间的相对速度分别为v01和v02。由相关流动法则[19]可知，各刚性块的速度矢量和相对速度均满足矢量闭合关系，于是便可建立该破坏模式相对应的速度场，如图3所示。

图3 破坏模式对应的速度场Fig.3 Velocity field for the failure mode

3 浅埋小净距隧道围岩压力新算法

3.1 先行洞左侧围岩压力计算

考虑两洞为对称分布，选取小净距隧道先行洞为研究对象，现对先行洞左侧拱顶垂直压力q1计算式进行推导。

1）速度矢量关系

根据相关流动法则和图3(a)可知，各速度间的矢量关系为：

2）重力功率Pγ左的计算

先行洞左侧岩体重力功率为刚性块ABFG 和BCE的重力功率之和，各刚性块的边长关系为：

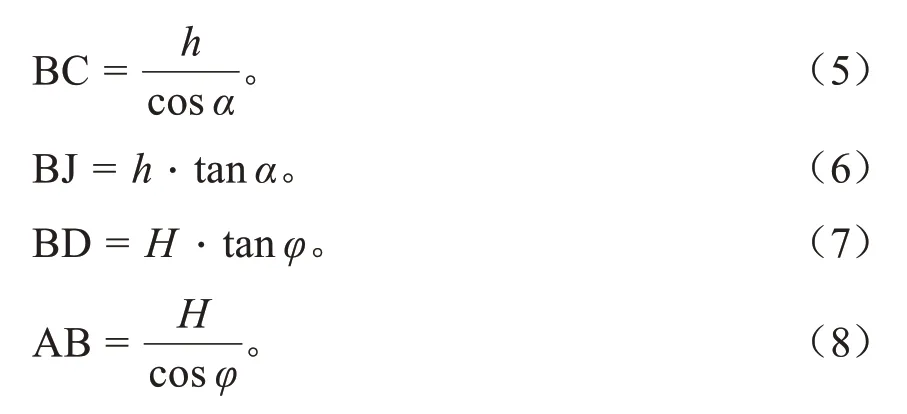
于是得到各刚性块面积为：

由式(4)～(10)可知，先行洞左侧重力功率Pγ左的计算表达式为：

其中，

式中：α为间断线BC 与CE 间的夹角，（°）；φ为内摩擦角，（°）；H为隧道埋深，m；h为隧道洞高，m；γ为容重，kN/m3。

3）内能散耗率Pc左的计算

内能散耗率Pc左的值等于各间断线DE、BC和AB上的内能散耗率之和，其计算式为：

其中，

式中：c为黏聚力，kPa；SD为滑动面。

4）支护反力功率PT左的计算

支护反力可阻止隧道围岩发生变形，故认为其值恒为负值，其计算式为：

其中，

式中：K为待定参数，一般取K=0.4～0.6[20]。

根据虚功率原理可知，PT左+Pγ左=Pc左，可计算得到竖向支护反力q1的表达式为：

5）围岩压力上限解的优化

由式（17）可知，当隧道开挖截面尺寸及埋深等参数确定时，由角度参数α确定围岩压力q1的上限解，同时确定小净距隧道外侧破裂面的形状。将围岩压力q1的求解问题转换为：角度参数在满足物理意义的约束条件下，求解出目标函数q1=f(α)的最大值。最大q1值才是对应破坏模式的最优化上限解，此过程可以运用MATLAB 数值软件，利用序列二次规划算法来实现。求解出q1后，根据ei=Kqi（i=1、2）求解水平围岩压力的大小。由图3(a)所示的速度场可知，各角度参数应满足以下约束条件：

3.2 先行洞右侧围岩压力计算

采用极限分析上限定理对先行洞右侧拱顶垂直压力q2计算式进行推导。

1）速度矢量关系

由图3(b)可知，v0、v2、v02间的速度矢量关系为：

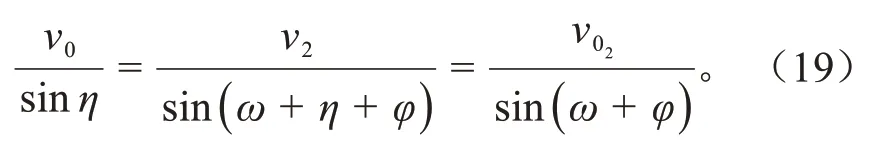
2）重力功率Pγ右的计算式为：

3）散耗功率Pc右的计算式为：

4）支护反力功率PT右的计算式为：

根据虚功率原理可知，PT右+Pγ右=Pc右，计算得到竖向支护反力q2的表达式为：

推导出q2表达式后，根据隧道围岩级别，按照式（27），求出破裂角β1的大小，再求解出角度ω的大小，将其代入式（23），便可求解出q2的计算值。

其中，

4 对比分析

隧道设计计算参数为：以Ⅴ级围岩为例，隧道开挖宽度B为16.7 m，埋深H为15 m，两洞间的净距D为5.66 m，开挖高度h为8.1 m，参照规范[17]选取围岩容重γ为20 kN/m3，φ、θ、φc分别为18°、27°、45°，黏聚力c为10 kPa，根据式（17）和式（23）计算，可得到垂直压力q1和q2。分别计算K=0.40～0.60 时垂直压力q1和q2的大小，并将本研究上限值和规范值进行对比，结果见表1。

表1 规范法与本研究计算结果对比汇总表Table 1 Comparison of calculation results obtained by the standard suggested method and our proposed method kPa

由表1 可知，随着系数K的增大，内外侧垂直压力逐渐减小，q1、q2间的差值不断扩大，内侧的围岩压力值始终大于隧道外侧的，表明：浅埋小净距隧道中隔岩柱侧为最不利，对其进行设计施工时应重点防护。相比于规范值，按本研究上限分析法得到的外侧围岩压力上限值偏小，而内侧压力上限值偏大，这是与小净距隧道破坏模式的构造等因素有关。当K值为0.4 时，本研究计算结果与规范值比较接近，表明：本研究按极限分析上限法计算浅埋小净距隧道围岩压力是合理可行的。

5 非线性系数m对围岩压力的影响

为研究系数m对围岩压力q的影响，以Ⅴ级围岩为例，取θ=27°、φc=45°，埋深H=20 m，单洞开挖跨度B=16 m，高h=10 m，两洞净距D=8 m，黏聚力c=50 kPa，取系数K=0.5，系数m为变化值，分别绘出m=1.1、1.2、1.3、1.4 时优化后的破坏模式如图4 所示。从图4 中可以看出，非线性系数m对浅埋小净距隧道围岩压力有着较大的影响，且随着非线性系数m的增大，小净距隧道两侧破裂面逐渐向外突出，破坏土体范围逐渐变大，围岩压力也随之增大，内侧破裂面不发生改变。

图4 非线性系数m对破裂面位置的影响Fig.4 Influence of nonlinear coefficient m on the position of fracture surface

6 结论

针对浅埋小净距隧道围岩压力，采用理论分析进行研究，得到结论为：

1）构造浅埋小净距隧道的破坏模式，并结合极限分析上限法和相关流动法则，建立与之对应的刚性块和速度场，推导出浅埋小净距隧道围岩压力半解析解表达式。

2）通过算例计算发现，当系数K较小时，上限值与规范值比较接近，验证了本研究计算方法的可行性。

3）非线性系数m对浅埋小净距隧道围岩压力有着较大的影响。随着系数m的增大，浅埋小净距隧道两侧破坏区域逐渐变大，围岩压力也随之增大。