混凝土相场断裂模拟
——影响裂纹宽度的因素
潘军,王鸿,赵冰,徐亚星,李涛峰,龙承运
(长沙理工大学 土木工程学院,湖南 长沙410114)
混凝土为重要的建筑材料,其断裂特性对工程安全起着关键作用[1]。可靠、高效的混凝土断裂模型在桥梁、隧道、大坝等土木工程结构的安全评估中发挥着重要作用[2]。对于混凝土断裂的研究,尤其是对其裂纹萌生和扩展的研究,引起了国内外学者越来越多的关注。近年发展起来的相场断裂法,通过跟踪阶参量自动演化获取裂纹路径,可方便地模拟出裂纹的动态扩展过程[3],为混凝土断裂数值计算方法提供了新的方法。
传统的混凝土断裂模拟方法有单元删除法、界面单元法和扩展有限元法(XFEM)等,是以不连续位移场来描述裂纹。其中,单元删除法和界面单元法只允许裂纹在网格边界扩展,存在明显的网格依赖性[4]。扩展有限元法(XFEM)[5]允许裂纹在网格内扩展,可以模拟出裂纹扩展的任意路径,但它在处理多裂纹问题时较为繁琐,大多用来处理单裂纹问题和简单的多裂纹问题。
相场断裂法用连续函数描述裂纹,其核心是引入阶参量描述材料的无损状态和完全破坏状态之间的各种状态。相场断裂法与其他方法相比,无需追踪裂纹的几何形状,在计算复杂裂纹扩展问题的扩展路径时具有独特优势。相场断裂方法可分为:①以物理学Ginzburg-Laudau理论为基础,可显示多种相场模型[6]的研究结果,该类模型能较好地模拟混合型断裂模型[7],但Griffith临界断裂能本构阈值Gc从未进入相应公式,还需适当选取退化(耦合)函数,其物理意义并不明确。②以脆性断裂变分理论为基础,Bourdin 等人[8]结合相场理论,给出了含阶参量断裂面的弥散表达式。由材料类型[9]、材料特性[10]、加载方式[11]等因素作用的多种静态相场断裂模型及推广至动态断裂[12-13]相场模型的结果表明:该类相场断裂模型与传统断裂理论的紧密联系,力学概念明确。
目前,相场断裂法应用于混凝土断裂问题的研究并不多见。Schlüter 等人[13]提出了预测准脆性材料断裂的相场模型,需预置初始裂纹。Mikelić等人[14]提出了可解决加压裂纹的相场模型,但裂纹局部网格较密,没有描述网格密度对裂纹的影响。Hirshikesh 等人[15]提出了准脆性材料相场模型,未能清楚描述长度尺度参数l0与裂纹的关系。因此,作者拟进行混凝土相场断裂的Abaqus 二次开发,研究单元尺寸和长度尺度等参数对裂纹宽度的影响,分析混凝土破坏机理,确定合理混凝土断裂参数,为混凝土结构的稳定性和安全性评估提供新的理论和计算方法。
1 混凝土的相场断裂模型
1.1 断裂总势能
混凝土的断裂总势能由体积储存能、裂纹表面能和外力做功三部分组成[8]:

式中:П为断裂总势能;Y为裂纹表面能;U为体积储存能;W为外力功;Gc为Griffith 临界断裂能本构阈值;ψ为体积储存能密度;V为被积体积;Γ为完全断裂的裂纹面;Sσ为应力边界;ui为位移;Ti为面力;fi为体力。
Bourdin 等人[8]在断裂变分理论的基础上,定义一个在[0,1]区间变化的标量φ为裂纹相场(阶参量)。当φ=1 时,表示有裂纹;当φ=0 时,表示材料完好。相场形式的裂纹表面能为:

对于二维问题,单位体积的裂纹表面密度函数γ(φ)的具体形式为:

式中:l0为控制裂纹“扩散”量的长度尺度参数。
体积储存能密度ψ由应变εij和阶参量φ共同确定:

式中:H(εij)为弹性应变能密度;Dijkl为弹性张量;εij、εkl为应变张量;g(φ)为应力退化函数。
g(φ)的表达式为:

式中:k≈10-6,使刚度矩阵在断裂模拟时保持良好的非奇异性。
由式(4)~(5),体积储存能U的表达式为:

1.2 相场断裂变分理论
不考虑面力的情况下,将式(2)、(3)、(6)代入式(1),断裂总势能的表达式为:

断裂总势能的一阶变分为:
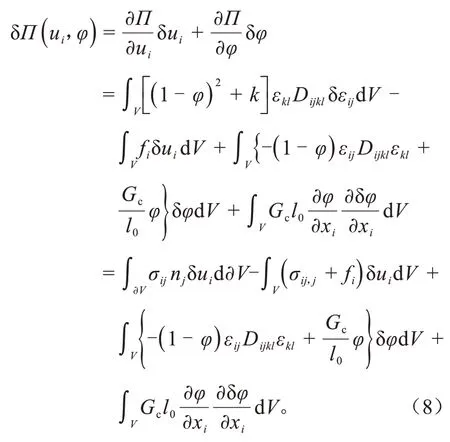
式中:nj为边界∂V外法线的方向余弦;为弹性应变能密度。
断裂变分理论认为,任意位置裂纹的任意动态扩展状态都会使总势能最小。即在平衡状态时,Dijklεkl为有效应力;δП=0对任意的δui和δφ都成立,则由式(8)得:
断裂问题的控制方程为:
σij,j+fi= 0。 (9)
断裂问题的相场演化方程为:

式中:∇为梯度。
力的边界条件为:
σijnj= 0。 (11)
相场的自然边界条件为:

相场断裂变分理论继承和发展了传统的Griffith 理论,并解决了Griffith 理论无法解决的裂纹萌生、扩展路径和失稳分叉等问题,为研究断裂问题提供了新的视角。
1.3 相场断裂模型的有限元形式
在平面应力状态下,单元内部一点的位移u与阶参量φ可以离散为:
u=Nuae,φ=Nφφe。 (13)
其中,ae={u1,v1,u2,v2,…,un,vn}T为单元节点位移向量;φe={φ1,φ2,…,φn}T为单元节点阶参量向量;n为单元节点数。
Nu=,为位移的形函数矩阵;Nφ=[ ]N1N2…Nn为阶参量的形函数矩阵。
单元内任意一点的应变ε与阶参量的梯度∇φ可由ae和φe表达式为:
ε=Buae,∇φ=Bφφe。 (14)
其中,
单元节点位移向量ae与单元节点阶参量向量φe用结构节点位移a与节点阶参量φ表达式为:
ae=Ga,φe=Gφ。 (15)
式中:G为单元集成的组装矩阵。
将式(13)~(15)代入式(7)中,结构总势能П的有限元形式为:

式中:ne为单元数。
由变分原理,总势能П的一阶变分为零,即:

δП=0对任意的δaT和δφT都成立,则:

平衡方程可改写为:

式中:Ku和Kφ分别为结构整体的位移和相场刚度,Pu和Pφ分别为结构位移和相场的整体荷载向量。


对式(18)~(19)做微分运算,得:

增量平衡方程可写为:

其中,

由于相场断裂有限元模型的方程组是非线性,因此,必须采用增量迭代来计算解。有限元软件Abquas 能解决许多复杂的非线性问题,被广泛应用工程计算中。选择在Abaqus 软件中建立模型,以便利用其内置的非线性求解器,采用牛顿-拉夫森算法和自动时间步进方案。先使用Abaqus 的用户自定义单元子程序UEL,定义新的二维四节点等参单元,该单元每个节点具有1个位移自由度和1 个相场自由度,共3 个自由度,UEL 还会计算单元的切线刚度矩阵和节点力向量。再编写1个用户自定义材料子程序(UMAT),该子程序用于公共块传递信息,并在积分点之间进行插值。本研究基于Abquas 的UEL 和UMAT 实现混凝土相场断裂的Abquas二次开发。
2混凝土相场断裂的模拟结果
2.1相场断裂模型的基本验证
通过单向拉伸试验,验证混凝土相场断裂模型的可靠性,得到应力应变曲线为[11]:
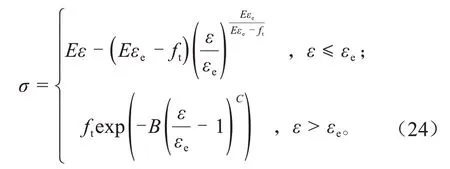
式中:B、C的取值分别为0.499 8、1.001 0。
试验材料的弹性模量E=25.5×103MPa,抗拉强度ft=1.5 MPa,泊松比μ=0.2,受拉峰值应变εe=1×10-4,本构阈值为Gc=15.500 50 N/m,长度尺度参数l0=0.018 48 m。混凝土单向拉伸试验与相场断裂模型的应力应变曲线如图1 所示。从图1 中可以看出,点B 为峰值应变εe对应的峰值应力点。当曲线处于AB 段时,ε<εe,单向拉伸试验与相场断裂模型的应力应变曲线吻合程度较好。当曲线处于BC 段时,曲线呈下凹趋势,此时材料处于软化阶段,裂纹开始萌生扩展,裂纹宽度随着应力的减小而不断增加,单向拉伸试验与相场断裂模型的应力应变曲线略有差别。当曲线处于CD 段时,材料处于裂纹贯通阶段,随着应变的增加,应力缓慢减小,单向拉伸试验与相场断裂模型的应力应变曲线吻合。表明:相场断裂模型能较好地模拟出混凝土的拉伸变形过程。

图1混凝土应力应变曲线Fig.1Stress strain curves of concrete
2.2 单元尺寸对裂纹宽度的影响
为研究单元尺寸对裂纹宽度模拟结果的影响,采用Abaqus的二维相场断裂模型,利用5组不同单元尺寸的网格对混凝土梁三点弯曲试验进行模拟。三点弯曲试样几何模型如图2所示,材料参数为:弹性模量E=25.5×103MPa,抗拉强度ft=1.5 MPa,泊松比μ=0.2,受 拉 峰 值应 变εe=1×10-4,本 构 阈 值Gc=15.500 5 N/m,长度尺度参数l0=0.018 48 m。5组不同单元尺寸网格单元的最小长度、宽度见表1。

图2 三点弯曲试验试件几何参数(单位:m)Fig.2 Geometry parameters of specimen in three point bending test(unit:m)

表1 网格单元尺寸Table 1 Grid element sizes m
在试件跨中顶部采用增量位移加载,初始位移为u0=10-6m,加载至u=7.70×10-5m,加载步Δu=10-6m,模拟结果如图3 所示。混凝土梁中性层的阶参数(裂纹)分布及不同的单元长度下的裂纹宽度如图4所示。
从图3 和图4(a)中可以看出,裂纹宽度随着单元尺寸的减小而变窄。当单元尺寸≤Mesh3 时,裂纹宽度趋于稳定。从图4(b)中可以看出,当裂纹完全贯穿部分,宽度的模拟结果随单元长度的减小而线性减小。当单元的长度足够小(趋于零)时,裂纹宽度收敛至0.003 92 m。可以认为收敛值是由理论模型决定的,与单元尺寸无关的物理量。

图3 不同单元尺寸下相场断裂模型三点弯曲试样的裂纹宽度Fig.3 Crack widths of three point bending specimens in phase field fracture model under different element sizes
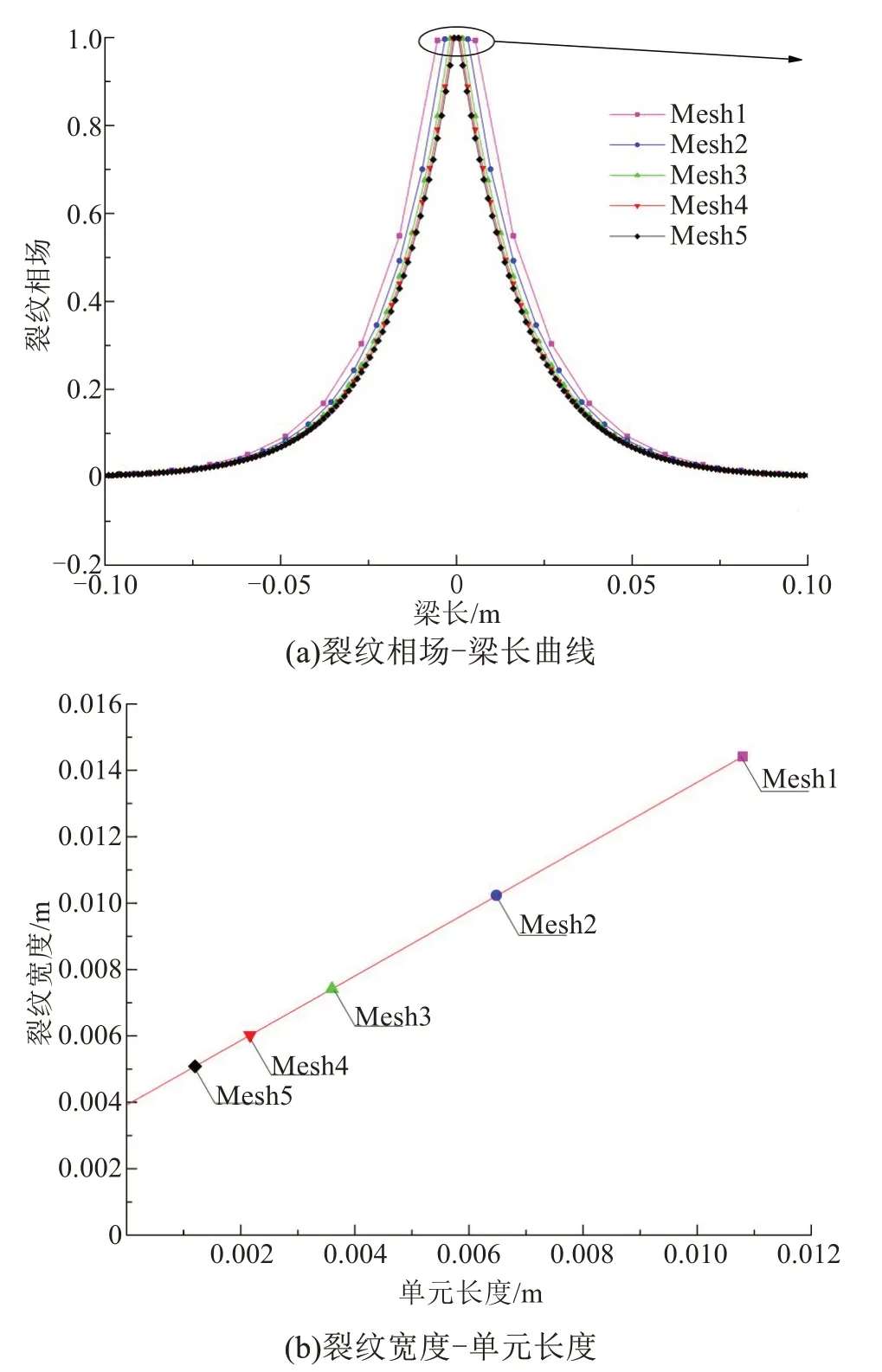
图4 相场断裂模型的三点弯曲试验值Fig.4 Values of three point bending tests obtained by phase field fracture model
2.3 长度参数对裂纹宽度的影响
为了研究长度尺度参数l0对裂纹宽度的影响,基于Abaqus 的二维相场断裂模型,利用Mesh4 网格,研究不同l0时,混凝土梁三点弯曲试验的裂纹扩展,其余的材料参数不变,模拟结果如图5 所示。混凝土梁中性层的阶参数(裂纹)分布及不同l0下的裂纹宽度如图6所示。
从图5 和图6(a)中可以看出,裂纹宽度随l0减小而变小,裂纹的弥散程度随l0减小而显著变小。从图6(b)还可以看出,裂纹宽度及弥散程度的模拟结果随l0减小而线性减小。当l0足够小(趋于零)时,裂纹的宽度收敛至零,表明:裂纹的宽度与l0呈正比例关系,可以认为裂纹宽度及裂纹弥散程度受l0控制。因此,在试验测得裂纹宽度的前提下,可以利用本数值模型,采用数值打靶法确定材料l0取值。

图5 不同长度尺度的相场断裂模型三点弯曲试验的裂纹宽度Fig.5 Crack widths of three point bending specimens in phase field fracture model under different length scale parameters


图6 不同长度的相场断裂模型三点弯曲试验值Fig.6 Values of three point bending tests obtained by phase field fracture model under different length scale parameters
3 结论
使用UEL 子程序实现相场断裂模型的Abaqus二次开发,编写了附加的UMAT 子程序,实现了相场断裂模拟结果的可视化。利用数值算例分析了单元尺寸和长度尺度参数对三点弯曲混凝土梁裂纹扩展宽度的影响。得到结论为:
1)混凝土相场断裂法可以较好地模拟出单向拉伸试验的全过程。
2)当单元尺寸足够小时,裂纹宽度是一个由理论模型决定、与单元尺寸无关的物理量。
3)裂纹宽度和裂纹弥散程度受长度尺度参数控制。

