圆形地连墙空间效应影响因素分析

张军，吴仁辉，张志超

（1.长沙理工大学 土木工程学院，湖南 长沙410114；2.广西交投科技有限公司 广西 南宁530022）

圆形地连墙以独特的“拱效应”在基坑支护中应用广泛，有关地连墙内力和变形的计算，大多基于弹性地基梁法和平面连续介质有限元法[1]，这两种方法适用于平面问题求解，没有考虑圆形地连墙空间效应[2-6]带来的三维受力和变形特性，有较大局限性。国内外学者针对圆形地连墙的空间效应开展了一些研究，沈健等人[7]比较了二维地基梁法、三维地基板法和三维连续介质有限元法分析圆形地连墙的计算结果，通过与实测数据对比，指出实测结果与三维地基板法更接近。刘明虎[8]以阳逻大桥圆形地连墙为实例，运用PAROI2 建立模型进行开挖模拟，再计算分析结果，得出地连墙径向水平位移、竖向弯矩、环向应力和内衬水平反力随着开挖深度的变化规律。申奇[9]运用有限差分软件FLAC 3D 进行了仿真模拟，探究了圆形围护结构半径、嵌固深度、墙厚对围护结构变形和受力的影响，并提出了相适应的优化设计方案。本研究针对圆形地下连续墙的空间受力特点，将圆柱壳有矩理论应用到圆形地连墙计算中，得到了圆形地连墙内力和变形的解析解，鉴于解析解的局限性，应用Midas GTS建立圆形地连墙的基本物理模型，得到了影响圆形地连墙空间效应的因素及其规律。

1 圆形地连墙空间受力的理论分析

圆形地连墙的内力和变形随着开挖深度的增加，以及墙体尺寸的变化而变化，这就是圆形地连墙的空间效应。圆形地连墙是一种三维空间结构，其分析计算是一个复杂的三维空间问题，圆形地连墙的结构特点[10-11]可以视为圆柱壳，运用薄壳有矩理论可以得到圆形地连墙变形和受力的解析解。

1.1 基本假定

采用基尔霍夫-乐甫假定：①壳体厚度t远小于中面最小曲率半径R；②壳体的变形和位移量都非常小，而且转角和应变是同级小量，在变形几何关系中可以忽略二次以上的高阶项；③中面法线方向的正应力分量远小于与法线垂直方向上的，前者在应力-应变关系中可忽略不计；④变形前中面的法线在变形后仍为法线，且在变形过程中，壳体厚度不变。

1.2 基本理论

建立坐标系，取薄壳中一个小微分块，R为薄壳的半径，x轴为微分块母线的方向，φ轴沿微分块的周向建立，z轴为微分块的径向方向，u、v、w的正方向分别为x、φ、z轴的方向，如图1 所示,再进行分析得出三大方程的表达式。

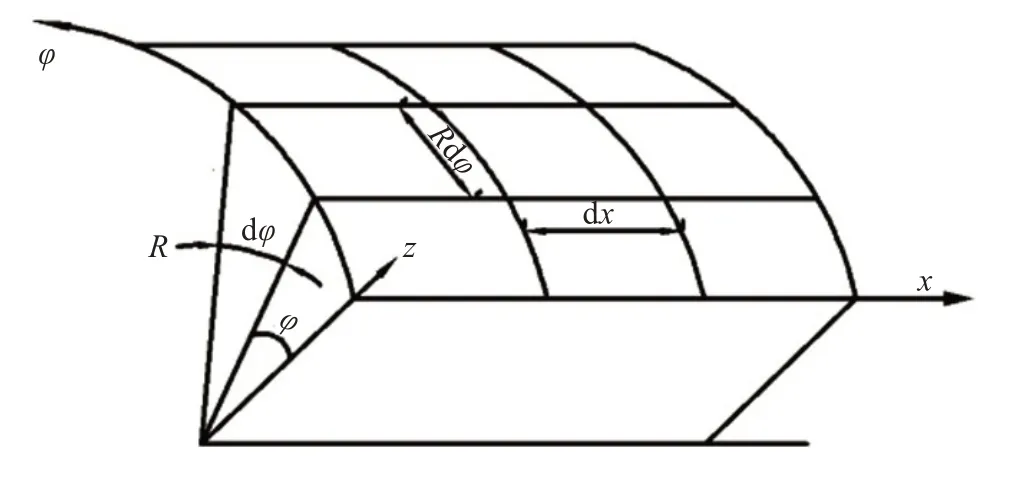
图1 圆筒壳体微分块Fig.1 Differential blocks of cylinder shell

1）基于kirchoff 假定，忽略微小变形壳体的几何方程为：

式中：ε、γ表示微元体中面的应变；k表示弯曲应变。

2）物理方程为：

3）在式（1）～（2）微分块中，取出dx×Rdφ的微元进行分析，得到平衡方程：

薄壳有矩理论应用到圆柱壳中，对圆柱壳体微元体进行分析，如图2所示。

图2 圆柱壳体微元Fig.2 Cylindrical shell elements

根据力的平衡条件可得：

引入变形条件，得到基本微分方程式：

式中：β为引入常数；w为径向变形；qz为内力。

求解式（5），并由材料力学中挠度与环向力、转角、弯矩、剪力的函数关系得到：

由式（6）可求得圆柱壳体结构的弯矩内力等值。

1.3 有矩理论在地连墙开挖时的应用

地连墙进行开挖时情况如图3所示。以开挖面为界，对开挖面上、下进行分析，如图4所示。

图3 圆形地连墙尺寸及开挖面位置示意Fig.3 Schematic diagram of circular diaphragm wall size and excavation face position

图4 圆形地连墙计算Fig.4 Calculation diagram of circular diaphragm wall

圆形地连墙开挖面以上部分，墙体只承受水土压力，其计算式为：

N1= -k0(γ0x)+q。 （7）

式中：k0为静止土压力系数；γ0为墙后土体加权平均重度；q为地表超载。

圆形地连墙开挖面以下部分，墙体承受基坑内侧及墙后的水土压力，其合力为：

式中：γ1为墙后各层土体的加权平均重度；γ2为基坑内侧各层土体的加权平均重度。

分别将其代入式（5），可得微分方程：

对式（9）～（10）进行求解。根据边界条件求得积分常数后，由开挖面处内力、位移的连续条件，结合地连墙挠曲方程，得到开挖面上、下的侧向位移、环向应力、竖向弯矩及剪力的计算公式为：

2 圆形地连墙空间效应的数值分析

2.1 基本模型的建立

采用有限元软件Midas-GTS 对不同工况下基坑的空间效应进行定量分析，将圆形基坑基本模型拟定为半径15 m，地连墙厚度1 m，墙高30 m，墙底部6 m嵌入基岩，基坑开挖深度18 m，基本模型的计算区域尺寸为120 m×120 m×50 m，土体与地连墙结构模型如图5～6所示。

图5 支护结构与模型Fig.5 Supporting structure and model

图6 地连墙模型Fig.6 Model of diaphragm wall

土体的本构模型采用修正Mohr-Coulomb 模型，这种本构模型是对Mohr-Coulomb 模型的改进，由非线性弹性模型和弹塑性模型组合而成，但相比于弹性理论，其更加接近塑性理论。Mohr-Coulomb模型可以模拟不受剪切破坏或压缩屈服影响的双硬化行为，该本构模型可以很好地体现土体加载和卸载时的刚度变化，对于基坑开挖类问题是一个很好的选择。为了真实准确的模拟出具有实际意义的结果，将基坑土体分为4层，基坑深度18 m，分6 次开挖，每次开挖3 m。土体单元类型选择三维实体单元，地下连续墙网格单元类型采用二维板单元来模拟，模型共有节点24 113 个，单元36 590 个，墙体采用均质各向同性线弹性模型，各个土层的物理力学参数以及地连墙的材料参数见表1，计算工况见表2。

表1 力学参数表Table 1 Mechanical parameter

表2 工况设置表Table 2 Working condition setting

在模型的两个侧面分别约束x、y2个方向的位移，模型底部约束x、y、z3 个方向的位移，而顶部为自由边界不约束任何方向的位移，随后对整个模型施加重力荷载，具体的施加如图7所示。

图7 边界约束及荷载分布Fig.7 Boundary constraints and load distribution

2.2 计算结果分析

2.2.1 地连墙厚度的影响

当地连墙厚度分别在0.50、0.75、1.00、1.25、1.50 m 4 种情况下，开挖至坑底时，地连墙的侧向位移如图8所示。

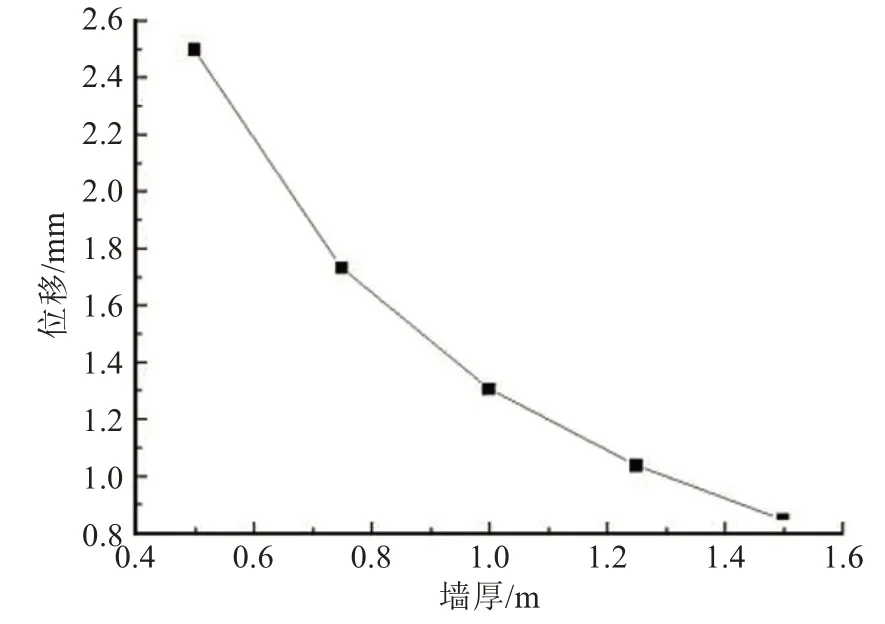
图8 墙体厚度不同取值时墙体侧移Fig.8 Lateral displacements of wall with different thicknesses

从图8中可以看出，随着墙体厚度的减小，地连墙的侧移不断增大，空间效应逐渐减弱。墙体厚度分别为1.50、1.25、1.00、0.75 m 时，墙体的侧移变化较为均匀，特别是墙厚1.50、1.25 m 时，地连墙的最大侧移变化量很小，在此范围内墙体厚度的变化对空间效应影响很小，空间效应较为明显，可以分析得出在此基础上继续增大地连墙的厚度对位移的影响不大。坑底以下16.5 m 处不同厚度的位移如图9所示。

当墙体厚度为0.5 m 时，墙体位移相比于之前3 组模型增长较快，地连墙侧移急剧增大，表明：地连墙厚度的取值对空间效应的发挥程度有影响。因此，在实际工程中，合理选择地连墙的厚度，既能完全发挥圆形地连墙空间效应，又能起到经济作用。圆形地连墙最大侧移与厚度关系为：

y=1.492 8x2-4.589x+4.396。 （12）

式中：y为地连墙侧移量；x为墙体厚度。

不同墙体厚度时，墙体的环向应力和竖向弯矩随深度的变化情况如图10～11所示。

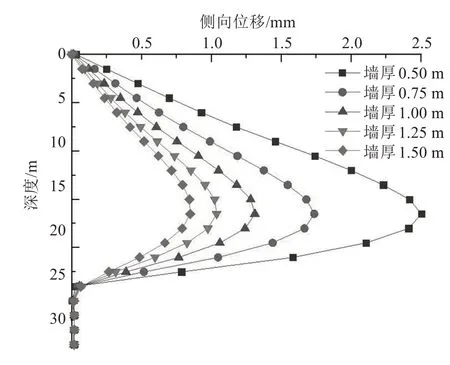
图9 墙体侧移随厚度的变化Fig.9 Variation of lateral displacements with wall thickness

图10 不同墙体厚度的环向应力变化Fig.10 Variation of circumferential stress with wall thickness

图11 不同墙体厚度的墙体竖向弯矩变化Fig.11 Variation of vertical bending moment with wall thickness

从图10～11 中可以看出，墙体厚度越大，环向应力越小，而墙体的竖向弯矩则越大。厚度每增加0.25 m，最大正弯矩分别增加43、57、56、54 kN·m，最大负弯矩分别增加70、70、80、78 kN·m。厚度的改变对于竖向弯矩的影响很小，而且均匀，最大正负弯矩出现的位置基本无变化。

2.2.2 开挖半径的影响

将基坑开挖半径分别改为25、35、55、75 m，同样取最后一个开挖步墙体的位移进行分析，如图12 所示。坑底下6 m 位置处不同开挖半径墙体侧移如图13所示。

图12 墙体厚度不同取值时墙体侧移Fig.12 Lateral displacements of wall with different thicknesses

图13 墙体侧移随半径的变化Fig.13 Variation of vertical bending moment with wall thickness

墙体的侧向位移随着开挖半径的增大而不断增大，整体变形仍呈现中间大两边小的趋势，同时侧移最大值点随着半径的增大不断上移。当半径为35 m 时，侧向位移最大值仅为5.3 mm；当半径75 m 时，最大侧移量增长到了16 mm，增长了近3 倍，表明：当开挖半径为75 m 时，墙体顶端已经开始出现位移。表明：基坑开挖半径对围护结构变形的影响作用很大，具有明显的空间效应。空间效应对于墙体位移的限制，随着半径的增大逐渐减弱，半径越大空间效应越不明显，但影响没有完全消失，也没有出现悬臂式的变形。同时，侧移的变化速率也随着半径的增大而不断增大，其变化并不是线性的，墙体半径越小，空间效应越强，所产生的空间效应对变形的控制能力就越强。圆形地连墙侧移随半径的变化关系为：

y=0.001 6x2+0.039 2x-0.562 6。 （13）

式中：y为地连墙侧移量；x为开挖半径。

不同开挖半径时，最后一个开挖步墙体的竖向弯矩与环向应力如图14～15 所示。从图14～15中可以看出，墙体的内力受半径影响很大，而且半径对弯矩的影响比对环向应力和侧移的要大，环向应力增长了近3倍，最大负弯矩随着半径的增长不断增长，而正弯矩变化很小。其中，半径为75 m 的基坑最大负弯矩约为半径为15 m 的50 倍，与改变厚度后的规律不同，随着半径的增大地下连续墙的竖向弯矩与环向应力都呈增大趋势，最大负弯矩出现在开挖面以下，最大环向应力出现于基坑的中上部，各个工况下环向应力与竖向弯矩最大值点的位置均略有上移。从增长速率来看，环向应力的增长速率逐渐减小，而弯矩的变化较为均匀，因为半径越大，地连墙的空间效应就越弱，墙体的拱效应越不明显，墙体受力模式逐渐向传统形式地连墙靠拢，地连墙环向应力所占比重逐渐减小，而竖向应力的比重逐渐增加。

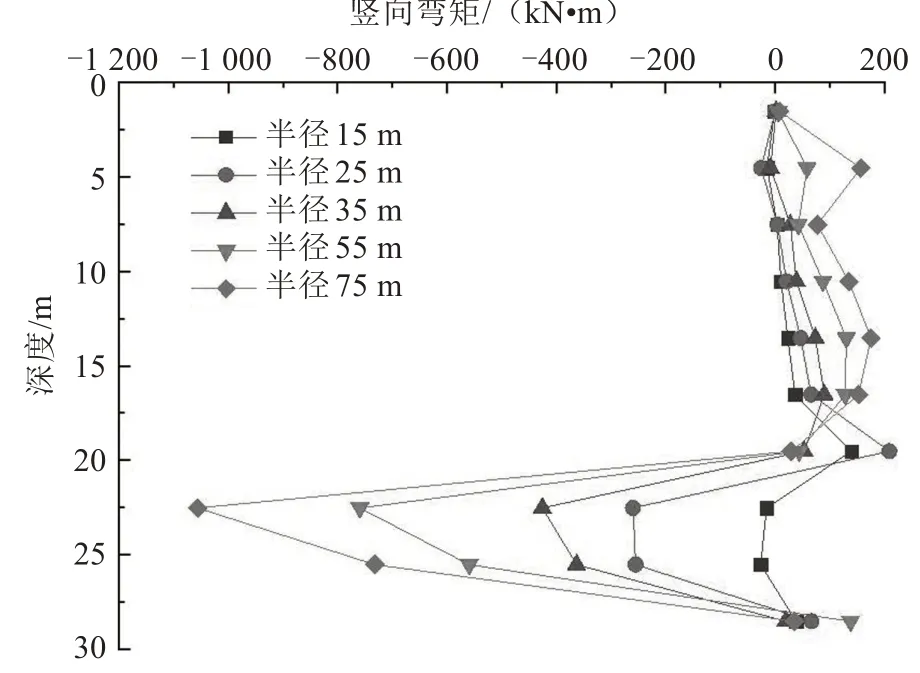
图14 不同开挖半径墙体的竖向弯矩Fig.14 Vertical bending moments of wall with different excavation radiuses

图15 不同开挖半径墙体的环向应力Fig.15 Circumferential stresses of wall with different excavation radiuses

2.2.3 嵌固深度的影响

在基本模型的基础上，改变围护结构的嵌固深度，分别取入土系数为0.7、0.5、0.4、0.3，即嵌固深度分别为14、10、8、6 m，研究不同嵌固深度对空间效应的影响。

由于5个模型的开挖深度都为18 m，仅嵌固深度改变。因此，不同嵌固深度的墙体高度是不同的，为了便于观察嵌固深度对空间效应的影响规律，取24 m 的墙体为研究对象，不同嵌固深度下最后一个开挖步墙体的侧向位移、竖向弯矩及环向应力如图16～18所示。

从图16～18中可以看出，除了嵌固深度取6 m时，改变嵌固深度对竖向弯矩、侧向位移和环向应力没有影响，不同嵌固深度下墙体最大侧移都发生在开挖面处。半径为15 m 的小尺寸圆形基坑存在着很强的空间效应，其本身的变形就很小，墙体本身就具有很好的受力模式。因此，嵌固深度的变化对空间效应的影响非常小，当嵌固深度变为6 m 后，基本上不存在负弯矩。无论是环向应力、竖向弯矩，还是侧移，都会有一定程度的突变。这是因为此时墙体全部嵌固在了软弱土层中，周围土层对墙底的约束能力减弱，所以墙体的侧移、环向应力和弯矩在开挖面以下都会出现一定的变化，随着墙体总高度的不断减小，其空间效应越来越强，环向作用也越强。嵌固深度的改变对空间效应的影响非常小，嵌固深度主要是约束墙底，嵌固段内墙体受力主要以弯矩为主。

图16 不同嵌固深度下墙体侧移Fig.16 Lateral displacement of wall under different embedded depths

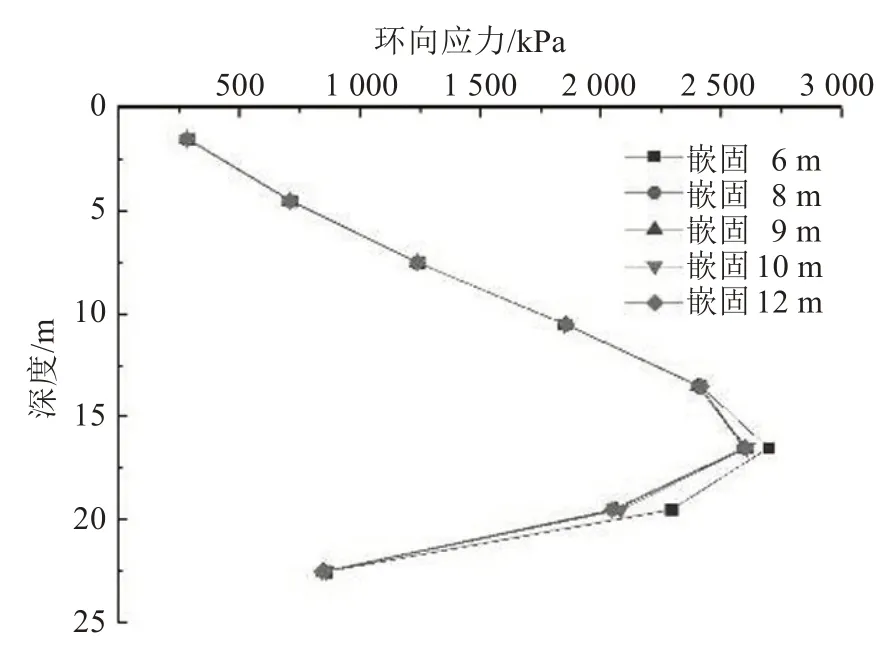
图17 不同嵌固深度下墙体的环向应力Fig.17 Circumferential stresses diagram of wall under different embedded depths

图18 不同嵌固深度下墙体的竖向弯矩Fig.18 Vertical bending moments of wall under different embedded depths

2.2.4 内衬厚度的影响

在基本模型的基础上，对墙体施加内衬，内衬的厚度分别为0.4、0.5、0.6、0.7、0.8 m。通过改变内衬的厚度，研究施工内衬对墙体空间效应的影响，如图19～22所示。

图19 内衬厚度不同时墙体的侧向位移Fig.19 Lateral displacements of wall with different thicknesses of lining

图20 内衬变化时墙体的竖向弯矩Fig.20 Vertical bending moments of wall with different linings

图21 墙体侧移随内衬厚度的变化Fig.21 Lateral movements of wall with different thicknesses of the lining

从图19～22 中可以看出，施加内衬与不施加内衬，其墙体位移趋势大致相同，随着内衬厚度的增加，墙体侧移量逐渐减小；随着开挖的进行，位移逐渐减小，墙体的最大位移仅变化了0.1 mm，其变化率占不施加内衬时最大位移的7%。同时，改变内衬厚度对墙体侧移影响非常小，并且其减少墙体侧移的程度是线性变化的，施加内衬及内衬厚度的变化对环向应力的与对侧移的影响规律相同，而对弯矩的非常小，可以忽略不计。

图22 内衬厚度变化时墙体的环向应力Fig.22 Circumferential stresses of wall with different thicknesses of the lining thickness changes

其中，墙体侧移与内衬的关系式为：

y=0.054 1x2-0.243 2x+1.308 9。 （14）

式中：y为墙体侧移量；x为内衬厚度。

2.2.5 土层参数的影响

土体的模量分别取基本模型弹性模量的0.9倍、1.0 倍、1.1 倍、1.2 倍、1.3 倍，其余参数保持不变，取最后一个开挖步墙体的侧移、弯矩与环向应力进行分析，分析土体弹性模量的改变对空间效应的影响，如图23～25所示。

从图23～25 可以看出，由于墙体嵌固条件良好，随着弹性模量的增加，基坑周围土体的环向效应逐渐增强，导致墙体的侧向位移与环向应力逐渐减小，但是其变化量很小，而且墙体最大侧移与最大环向应力发生的位置没有改变。在基坑顶面以下15 m 范围内，侧向位移与环向应力基本没有任何变化。土体弹性模量的改变，仅对基坑底面一定范围内墙体的侧移和环向应力有影响，同样在开挖面以上，墙体的竖向弯矩也几乎没有变化，随着土体弹性模量的改变，最大正负弯矩都出现一定减小，但是减小量不大。

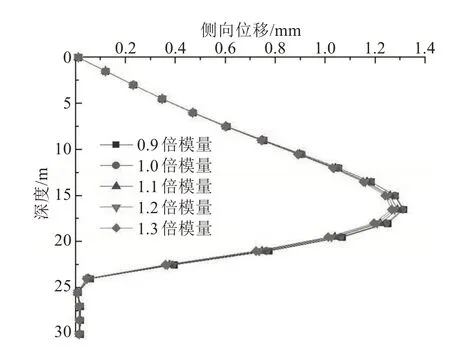
图23 土体弹性模量不同时墙体的侧向位移Fig.23 Lateral displacement of wall with different elastic modulus of soil

图24 土体弹性模量不同时墙体的竖向弯矩Fig.24 Vertical bending moments of wall with different elastic modulus of soil

图25 土体弹性模量不同时墙体环向应力Fig.25 Circumferential stresses of wall with different elastic modulus of soil

3 结论

圆柱壳有矩理论应用于地连墙中，建立解析解，并通过Midas GTS软件建立计算模型，对圆形地连墙的受力性能影响进行分析，得出结论为：

1）圆形地连墙开挖存在明显的空间效应，侧移呈现两端小中间大的分布规律，坑外地表沉降最大值较小，其发生的位置随着开挖的进行逐渐向远离基坑的方向发展，墙体环向应力的分布规律与侧向位移的一致，地连墙最大正负弯矩均出现在开挖面以下，开挖面以上弯矩变化很小，存在很明显的正负弯矩区。

2）空间效应对开挖半径的变化非常敏感，随着半径的增大，墙体最大侧向位移与环向应力不断增大，最大正弯矩变化很小，而最大负弯矩显著增大。当开挖半径超过55 m 时，墙体顶端已经开始出现侧移，空间效应对位移与内力的限制作用已经非常微弱。

3）墙体的嵌固深度对空间效应的影响非常小，仅对坑底及嵌固部分的一定范围内墙体的内力和位移有影响，但总体影响不大。

4）墙体厚度的变化对空间效应影响是非线性，墙体环向应力与侧向位移随墙体厚度的增加变化率不断减小，而竖向弯矩变化则较为均匀。

5）设置内衬与不设内衬对空间效应有一定影响，侧向位移变化率为7%，而对弯矩几乎没有影响，内衬厚度的变化对内力和位移的影响也很小。

6）土体弹性模量的变化可以增强基坑周围土体的环向应力，而对地连墙的空间效应影响有限，仅集中影响坑底附近。