分类讨论思想在“相交线”概念教学中的应用

黄华

[摘  要] 分类讨论常用于较复杂的数学概念、运算、动点或图形不确定等情况的分析，它能有效简化问题，降低难度，文章以“相交线”概念教学为例，阐述分类讨论思想在概念教学中的应用策略：创设情境，初步感知分类思想;合作交流，切实体会分类过程;适当练习，形成分类讨论思想.

[关键词] 分类讨论;概念教学;合作交流

分类讨论是指将复杂的问题分割成几个基础性的小问题，再逐个突破的思想策略，常用于较复杂的数学概念、运算、动点或图形不确定等情况的分析. 它需有确定的分类对象，按照统一的标准进行分类，做到不重复、不遗漏. 将分类讨论思想应用于数学概念教学中，能有效地简化概念的难度.

“相交线”章节涉及较多关于角的位置关系的概念，因位置关系多而导致了概念数量也很多，学生一不小心就会出现概念的混淆. 为了帮助学生在学习初始阶段就能厘清各个概念之间的关系，避免后期因概念不清而在几何证明中漏洞百出，笔者特将教学内容与分类讨论相结合.

创设情境，初步感知分类思想

教学应关注学生对知识的理解程度，让学生感知知识与知识间存在的内在联系. 概念作为每个知识点的起点与基础，在教学中具有无可替代的重要作用. 在概念教学的初始阶段，创设丰富的情境可让学生在心理上对概念产生共鸣，让学生在知识与生活的交互中感知概念的形成与发展过程.

对于一些复杂的概念，我们可在情境中设置相应的分类点，让学生在探索中自主发现分类的标准，并将自身的生活经验、记忆与思维凝聚到一起，增进对概念的理解. 如“相交线”涉及的概念教学，可创设以下情境进行课堂导入.

教师结合剪刀、钟表指针、夹钳等常见的生活物品创设情境，让学生从中抽象出两根直线相交的基本模型.

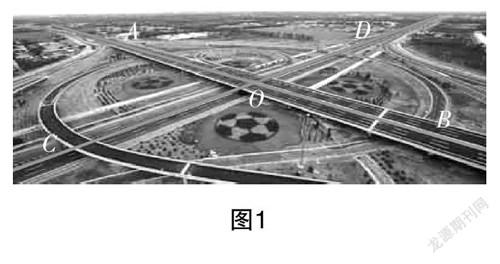
师：观察图1，你们看到什么？

生1：看到公路、高架桥等呈交叉的关系.

师：现在我们一起将图中标注了AB与CD的两根直线画出来. 根据图1抽象而来的图像见图2.

师：观察图2，你们能看到几个角？

生2：4个角.

师：若两两分组，一共可组成几组？

生3：六组.

师：如果将这六组角分类，可用什么标准分？（小组合作讨论）

生4：有相邻的和相对的两种分类方式.

师：不错. 分类后角与角之间的度数是否有什么特别的地方？

生5：处于相对位置上的两个角的边在一条直线上，互为反向延长线，同时它们的顶点与角度大小都一样;处于相邻位置上的两个角有一条公共边，还有一条边是互为反向延长线的关系. 它们拥有共同的顶点，且两角度数相加为180°.

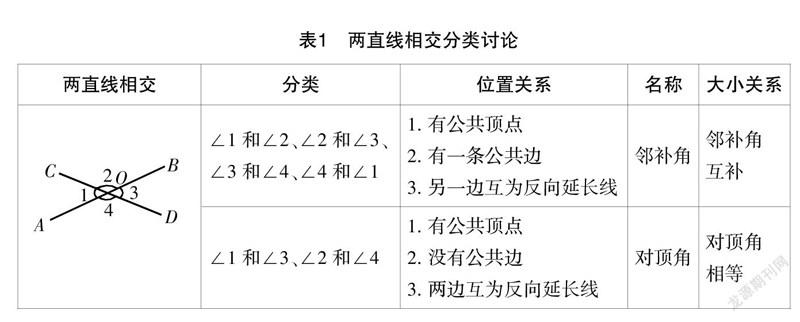
师：非常好！这就是我们今天所要认识的邻补角和对顶角. 如表1，是两直线相交的分类讨论情况及角与角之间的位置关系.

师：根据表1可知，对顶角是相等的关系. 那么，我们怎么能确定它们相等呢？有没有办法加以证明？

生6：如图2，已知∠AOC+∠COB=180°，∠COB+∠BOD=180°，所以∠AOC=∠BOD，同理可证得∠AOD=∠COB.

师生有效互动，激发了学生对“相交线”的学习兴趣. 学生在教师逐层递进的引导下通过自主讨论，获得六组角的分类标准分别有相邻的与相对的两种. 在这两类角的观察中，逐渐获得相应的概念. 由此可见，分类讨论思想在概念形成的初始阶段就具有开拓学生思维的作用，教师可多加引导，帮助学生快速获得概念的内涵与相应的数学思想.

合作交流，切实体会分类过程

为了强化学生对概念的认识，可选择小组合作的方式鼓励学生在交流中共同完成学习任务. 当相交线为三根时，会出现更多的角，这些角之间具有怎样的关系，该如何分类进行讨论是合作交流的主题. 为此，课堂呈现出以下教学片段.

首先向学生介绍截线和被截线的定义，为接下来的教学做好铺垫.

师：大家对两根线组成的四个角的关系已经有了一定的认识，现在我们在两条线的基础上再添加一条直线，大家来数一数有几根线、几个角.

生7：如图3，有a，b，c三根直线，这些直线相交后得到8个角.

师：刚刚我们已经探究过有公共顶点的两个角的关系（对角与邻角），现在将没有共同顶点的角进行两两分配，可组成多少组？（学生合作交流，得到有16组的结论）

师：那我们来逐组进行分析，先看看∠1和∠5，这两个角之间的位置关系是怎样的？

生8：∠1和∠5都在截线的同一侧，且在被截线的同一个方向.

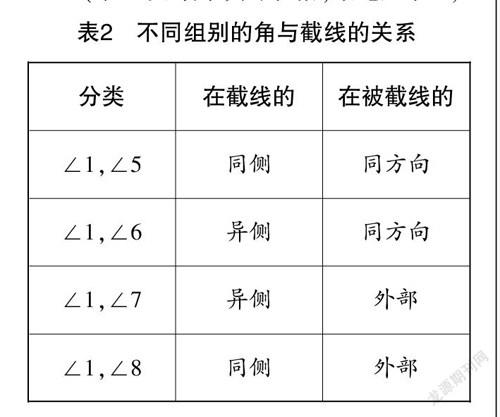
师：很好！那现在请大家将不同组别的角与截线的关系填到一个表格内.

（学生设计并填写表格，结论见表2.）

师：现在请各小组讨论，分别描述每组角（两个角为一组）之间的位置关系，并分类.

（学生合作学习，教师引导.）

结论：根据角与角之间的位置关系，分别获得同内角、同同角、同外角、异内角、异同角和异外角六种.

师：本节课我们学习其中的三种，即同内角、异内角和同同角. 我们分别给它们起一个新的名字为：同旁内角、内错角与同位角. 现在请大家仔细观察这三种角，说说它们有没有什么能让人一眼就看出来的特征.

生9：同旁内角呈现一个U字形，内错角则呈现出Z字形，而同位角在同一个方向，差不多是一个F形.

学生在合作交流过程中对角的位置关系逐个进行分类，并针对教师所提出的三类角进行研究，获得了一定的成效. 尤其是用大写的英文字母表示不同类型角之间的位置关系，这种方式简洁而又深入人心. 合作过程中，组内每个成员都切实体会到了数学分类的方法与过程，这为培养学生的数学思想奠定了一定的基础.

适当练习，形成分类讨论思想

课堂练习可促进知识的形成与巩固，概念学习也离不开练习的辅助. 为了帮助学生形成良好的数学思想，练习设计时需有针对性地添加相应的元素，让学生在独立思考中实施分类讨论，以灵活思维深化对概念的理解，达到学以致用的目的.

课堂小练：

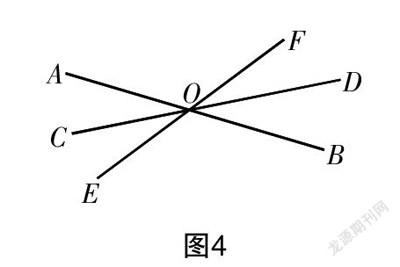
1. 如图4，已知直线AB，CD，EF相交于点O，则∠AOC的对顶角是______，邻补角是______.

2. 观察图5，其中∠1，∠2互为对顶角的有哪些？

3. 观察图6，∠2，∠3称为_____角;∠2，∠4称为_____角;∠2，∠5称为_____角;∠2，∠6称为_____角;∠2，∠8称为_____角.

4.如图7，直线AB，CD，EF相交于点O，已知∠1=30°，∠2=65°，则∠3为多少度？

学生在完成練习的过程中再一次感知直线相交所形成角的位置关系，1、2两题着重考查学生对对顶角与邻补角的理解程度，其中第1题中的第2问∠AOC的邻补角有哪些，不少学生只写了一个答案，而根据邻补角的概念，符合条件的角应有两个. 学生只有在深刻理解了邻补角内涵的基础上，才不会漏解.

3、4两题主要考查学生对同旁内角、同位角与内错角的认识程度. 第3题看似题量大，其实只要掌握每种角相应的位置关系，答题并不困难. 笔者要求学生根据自己探究、总结出来的用英文字母表示的相交线形状进行判断，准确率较高. 第4题则考查学生对知识的掌握与应用程度，练习赋予角明确的度数，学生根据角与角之间的位置关系与度数关系可求出答案.

这一组试题的设计，从学生的认知经验与授课内容出发，学生在练习过程中深化了对各个概念的理解，并实现了举一反三、灵活应用所学知识. 解题中，学生需将每一种角的位置关系进行观察、梳理、分类讨论，从而有效地促进了学生分类讨论思想的形成.

总之，数学思想方法的培养并非一朝一夕就能完成的，它需要教师紧跟新课改的步伐，不断更新教育理念，充分发挥学生的主体作用，让课堂成为学生思维成长的阶梯. 当然，更重要的是让学生深度参与课堂教学的全过程，感悟用分类讨论的方法学习的过程，为数学核心素养的提升奠定基础.